Hey math friends and happy Wednesday! Today we are going to take a look at the infinite geometric series formula in summation notation. First, we’ll review what a geometric sequence (or geometric progression) is, then look at the difference between divergence and convergence based on the common ratio, and then finally look at the formula. The unique thing about infinite geometric sequences is that the formula doe snot always apply. We only know if the formula applies to our series based on the value of the common ratio.
This may sound a bit complicated, with a few new concepts, but fear not as divergence and convergence are easy to identify! If you have any questions, don’t forget to check out the video and practice problems below. Happy calculating! 🙂
What does it mean to find the “Sum of Infinite Geometric Sequence” (Series)?
We already know what a geometric sequence is: a sequence of numbers that forms a pattern when the same number is multiplied or divided by each successive term.
The number is multiplied or divided to each term is called the common ratio. We can see below that each number in the sequence is being multiplied by 1/2. Therefore, we can say that the common ratio of the geometric sequence below is 1/2.
Example:
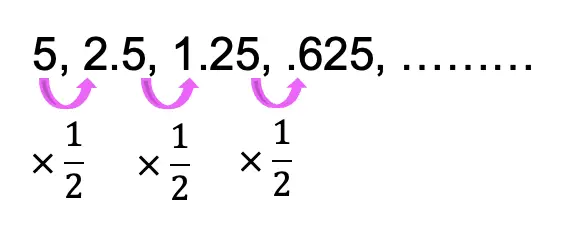
But then, what happens if we wanted to sum all the terms of our geometric sequence together? The sequence of terms is now considered to be an infinite geometric series since we are summing all of the terms of our series together, infinitely. Take a look below:
Example:
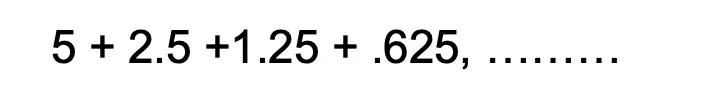
Summation Notation:
We can also write our infinite geometric series using something called Summation Notation shown below. This is a different format, also known as sigma notation, if you need a refresher on how to use and read summation notation, please check out the link in this paragraph. When writing in summation notation, we are actually writing the sum of the geometric series in a different way. Check it out below:
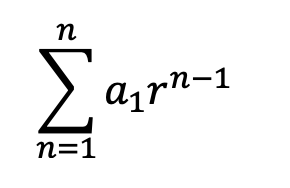
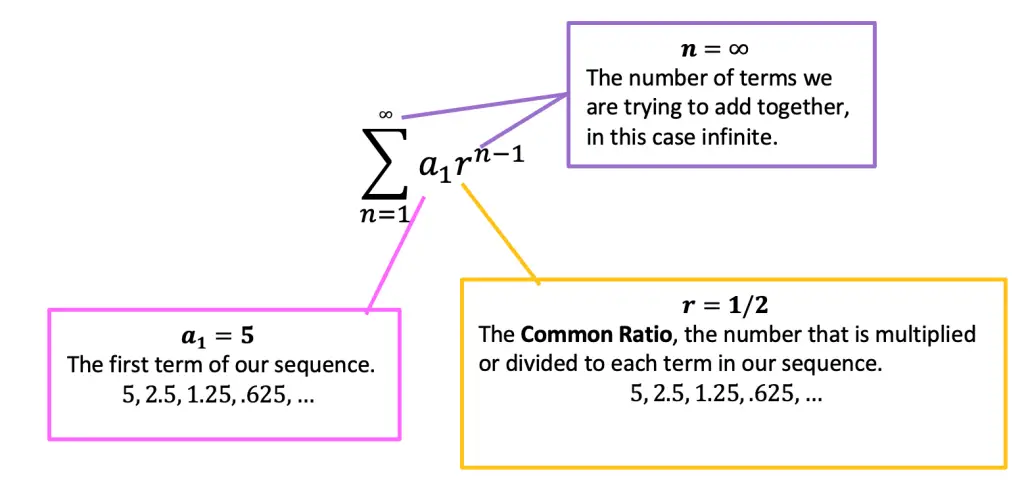
Now that we know what each part of this summation notation looks like, let’s actually identify what each part of this equation means in relation to our geometric sequence:
a1=The first term. In this case, we can see that the first term of our geometric sequence is the number 5 in the example below. Therefore, we can say a1=5.
r= The common ratio is the number that is multiplied or divided by each consecutive term within the sequence. In the example below, each number is multiplied by 1/2, therefore we can say, r=1/2.
n= The total number of terms we are trying to sum together. In the example mentioned below, we are trying to sum an infinite number of terms, so in this case, n starts at 1 and then continues infinitely to increase by 1 for each subsequent term.
If we were to expand our inifite series summation it would look something like this:
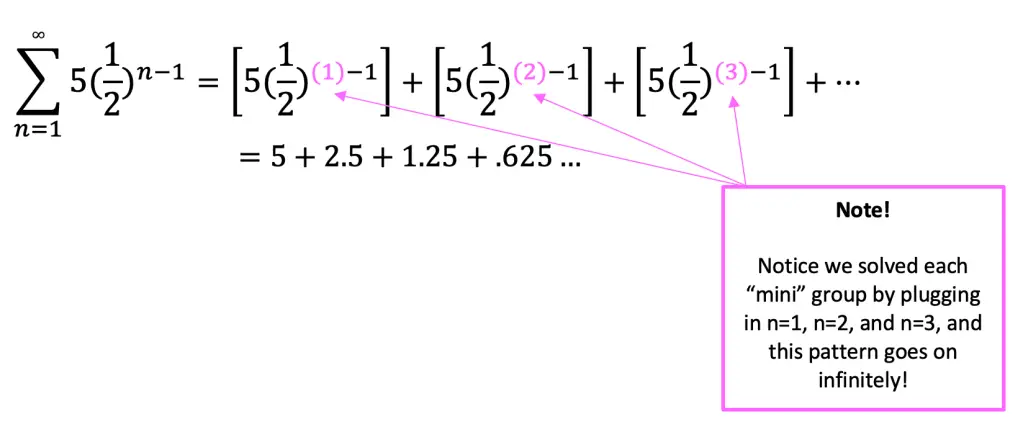
But how would we calculate this? This is an infinite series represented in summation notation, therefore, it goes on infinitely, how does this work?
That’s where our Infinite Geometric Series formula comes in handy! But before we jump into finding a solution and looking at our formula, let us take a closer look at what types of geometric series qualify for using the infinite series formula in the first place.
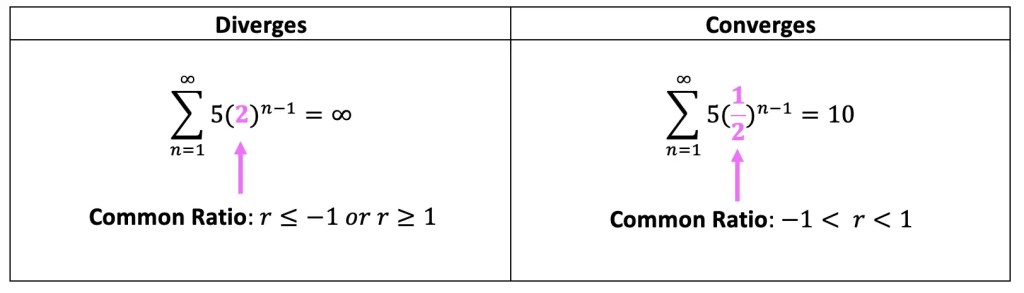
Divergence Vs. Convergence: When do we use the Infinite Series formula?
There are two types of Infinite Geometric Series:
Type 1: Infinite Geometric Series that diverges to infinity
Type 2: Infinite Geometric Series that converges to a numeric value (-1 < r < 1)
Check out the differences in the example below:
Infinite Geometric Series Formula:
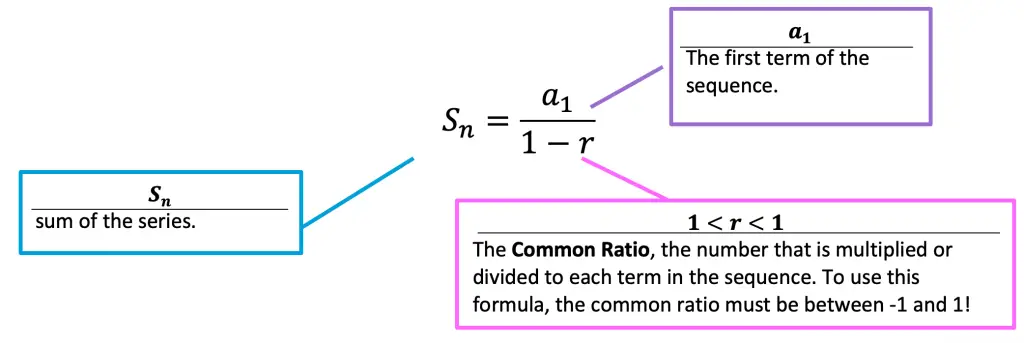
Now the moment you’ve all been waiting for… the Inifite Geometric Series Formula! Remember, the use of this formula is purely based on the common ratio of our geometric sequence.
The infinite geometric series formula can only be used if the common ratio, r, is less than 1 and greater than -1. If the common ratio, r, is not between -1 and 1, then the sum of the geometric sequence diverges to infinity (and the formula cannot be used).
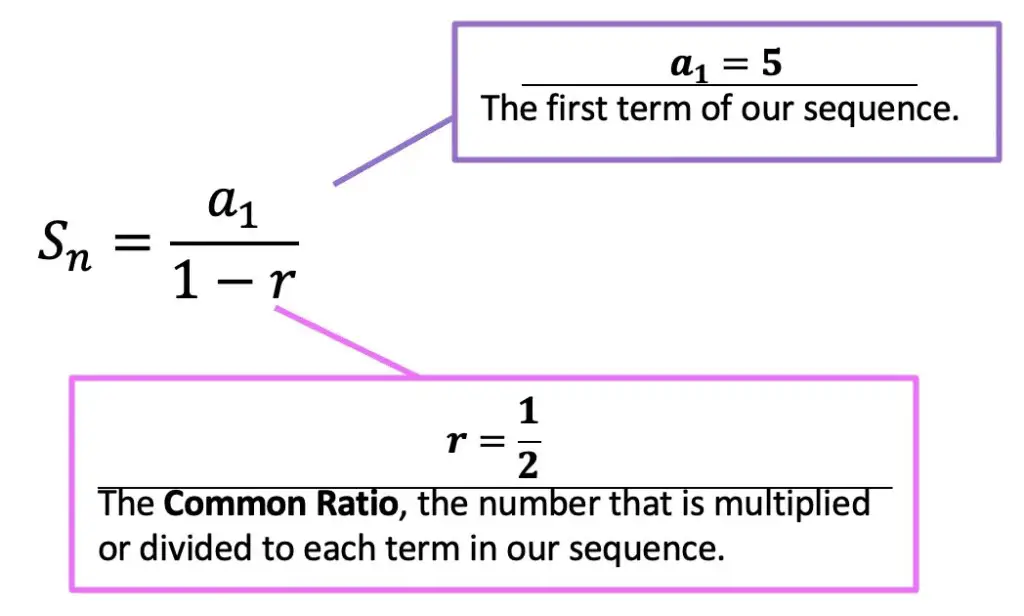
Now that we have the formula to work with and know when to use it (when -1 < r < 1), let’s take another look at our question and apply our infinite geometric series formula to find a solution:

Step 1: First, let’s identify the common ratio to make sure that it is between numbers -1 and 1. If the common ratio is a fraction between these two numbers, then we can use our infinite series formula.

Step 2: Now that we know we can use our infinite series formula, let’s write out each part of the formula and identify what numbers we are going to plug in.
Step 3: Last but not least, let’s fill in our formula with the correct numbers and solve with the given values.
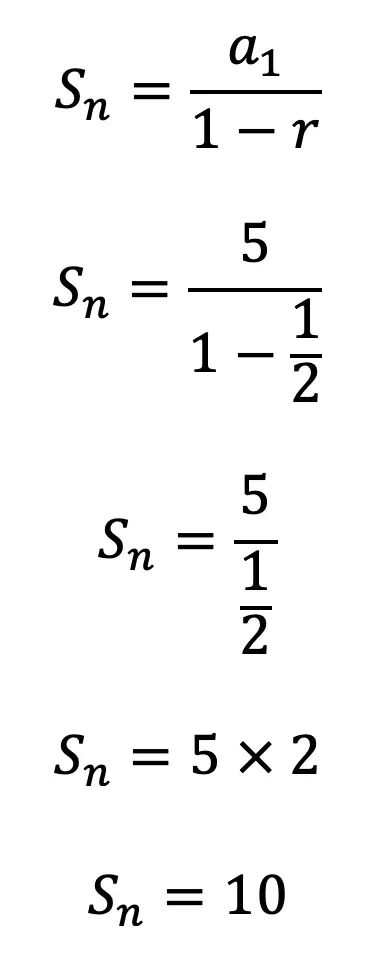

Think you are ready to try inifite geometric series examples on your own? Check out the following infinite geometric series practice questions below to determine if a series converges or diverges.
Practice Questions:
State if each given series converges or diverges, then if applicable find the solution.

Solutions:

Related Posts:
Looking to learn more about sequences? You’ve come to the right place! Check out these sequence resources and posts below. Personally, I recommend looking at the finite series posts next including: finite geometric sequence or finite arithmetic series!
Arithmetic Sequence (arithmetic progression)
Golden Ratio in the Real World
Still, got questions? No problem! Don’t hesitate to comment below or reach out via email. And if you would like to see more MathSux content, please help support us by following ad subscribing to one of our platforms. Thanks so much for stopping by and happy calculating!

Great post! Love learning about sequences
Thank you! Nothing like a good sequence!