HighSchool Archives - Math Lessons

How to Construct Altitudes of a Triangle ⊿

Advertisements

Hi everyone and welcome back to another week of MathSux! For this week’s math lesson, I bring to you four constructions in one in How to Construct Altitudes of a Triangle using a compass and straight edge. In the video and post below we will define what an altitude is, find the altitude of an acute triangle, an obtuse triangle, and a right triangle. Just a reminder that an acute angle is an angle that is less than 90 degrees, an obtuse angle is an angle that is greater than 90 degrees and a right angle is an angle equivalent to 90 degrees. And lastly, within this post, we will use our construction to define and discover the orthocenter of a triangle, which is the point at which the altitude of each part of the triangle intersects.

I hope you find the below video helpful and interesting! Please let me know in the comments below if you have any questions. Good luck and happy calculating!

How to Construct Altitudes of a Triangle:

What is an Altitude of a Triangle?

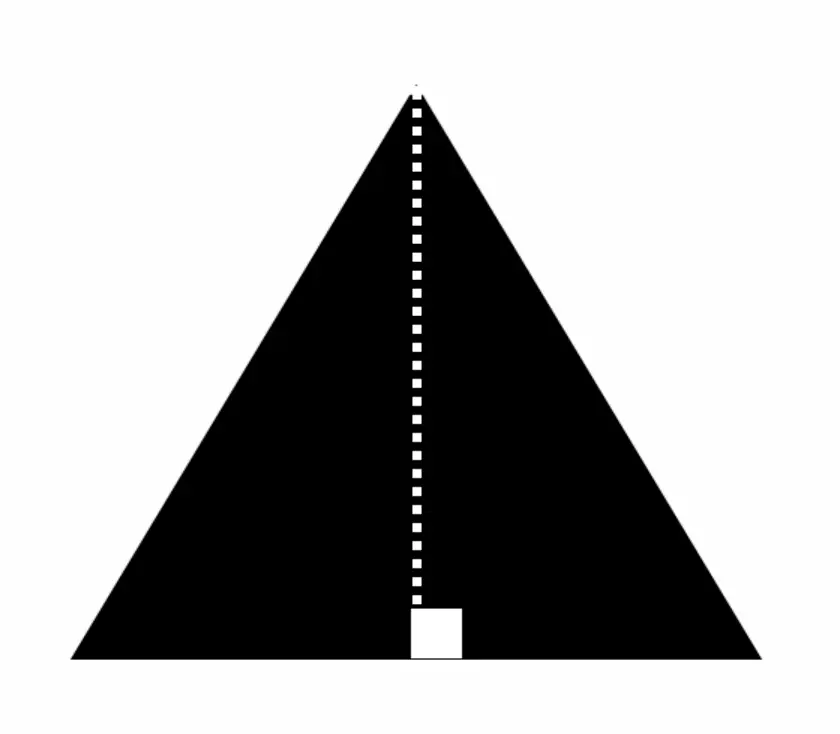
An Altitude is a perpendicular line drawn from the vertex of a triangle to the opposite side, creating a 90º angle (or right angle). Check out the example in the picture below, where the white dotted line drops down from the vertex of the triangle to the opposite side and how it forms a 90-degree angle represented by the white square. This is an altitude!

How to Construct the Altitude of a Triangle

In the video above, we will look at how to find the altitude of an acute triangle, an obtuse triangle, and a right triangle step by step. Please watch the video above before reading the next part of this post about the orthocenter. This will makes things a bit clearer!

How to Find the Orthocenter of Triangle with a Compass:

Now that we have found the altitudes of an acute triangle, obtuse triangle, and right triangle (in the video above), we can easily use our tools and knowledge of constructions and altitudes to find the orthocenter of a triangle.

The Orthocenter is a point where all three altitudes meet within a triangle. We can see in the example below, each dotted line represents an altitude to each vertex of the triangle.

In order to find the orthocenter using a compass, all we need to do is find the altitude of each vertex. The point at which they meet in the middle is known as the orthocenter. Check out the video above to see how this works step by step using a compass and straight edge or ruler.

Constructions and Related Posts:

Looking to construct more than just the altitude of a triangle? Check out these related posts and step-by-step tutorials on geometry constructions below!

Construct an Equilateral Triangle

Perpendicular Line Segment through a Point

Angle Bisector

Construct a 45º angle

Square Inscribed in a Circle Construction

How to Construct a Parallel Line

Bisect a Line Segment

Construct a Parallel Line

Best Geometry Tools!

Looking to get the best construction tools? Any compass and straight-edge will do the trick, but personally, I prefer to use my favorite mini math toolbox from Staedler. Stadler has a geometry math set that comes with a mini ruler, compass, protractor, and eraser in a nice travel-sized pack that is perfect for students on the go and for keeping everything organized….did I mention it’s only $7.99 on Amazon?! This is the same set I use for every construction video in this post. Check out the link below and let me know what you think!

Still got questions? No problem! Don’t hesitate to comment with any questions below.

Facebook ~ Twitter ~ TikTok ~ Youtube

And if you’re looking for more lessons on triangles, check out these related posts below:

Congruent Triangles

Similar Triangles

45 45 90 special triangles

30 60 90 special triangles

Similar Triangles

Legs of a Right Triangle (when an altitude is drawn)

Combining Like Terms and Distributive Property: Algebra

Advertisements

Greetings math peeps! In today’s post, we are going to review some of the basics: combining like terms and distributive property. It’s so important to master the basics such as these, so you’re prepared and ready to handle the harder stuff that’s just around the corner, trust me they’re coming! And for those who already feel comfortable with these topics, great! Skip ahead and try the practice questions at the bottom of this post and happy calculating! 🙂

When do we combine “like terms?”

Combining like terms allows us to simplify and calculate our answer with terms that have the same variable and same exponent values only. For example, we can combine the following expression:

How do we combine like terms?

We add or subtract the whole number coefficients and keep the variable they have in common.

Why? We could not add these two terms together because their variables do not match! 2 is multiplied by x, while 3 is multiplied by the variable xy.

Why? We could not add these two terms together because their variables and exponents do not match! 2 is multiplied by x, while 3 is multiplied by the variable x^2 . Exponents for each variable must match to be considered like terms.

Distributive Property:

Combining like terms and the distributive property go hand in hand. The distributive property rule states the following:

There are no like terms to combine in the example above, but let’s see what it would like to use the distributive property and combine like terms at the same time with the following examples:

Example #1:

Example #2:

In some cases, we also have to distribute the -1 that can sometimes “hide” behind a parenthesis.

Try the following questions on your own on combining like terms and the distributive property and check out the video above for more!

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂

Looking to review more of the basics? Check out this post on graphing equations of a line y=mx+b here.

Facebook ~ Twitter ~ TikTok ~ Youtube

Imaginary and Complex Numbers: Algebra 2/Trig.

Advertisements

Happy Wednesday and back to school season math friends! This post introduces imaginary and complex numbers when raised to any power exponent and when multiplied together as a binomial. When it comes to all types of learners, we got you between the video, blog post, and practice problems below. Happy calculating! 🙂

What are Imaginary Numbers?

Imaginary numbers happen when there is a negative under a radical and looks something like this:

Why does this work?

In math, we cannot have a negative under a radical because the number under the square root represents a number times itself, which will always give us a positive number.

Example:

But wait, there’s more:

When raised to a power, imaginary numbers can have the following different values:

Knowing these rules, we can evaluate imaginary numbers, that are raised to any value exponent! Take a look below:

-> We use long division, and divide our exponent value 54, by 4.

-> Now take the value of the remainder, which is 2, and replace our original exponent. Then evaluate the new value of the exponent based on our rules.

What are Complex Numbers?

Complex numbers combine imaginary numbers and real numbers within one expression in a+bi form. For example, (3+2i) is a complex number. Let’s evaluate a binomial multiplying two complex numbers together and see what happens:

-> There are several ways to multiply these complex numbers together. To make it easy, I’m going to show the Box method below:

Try mastering imaginary and complex numbers on your own with the questions below!

Practice:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Don’t forget to sign up for FREE weekly MathSux videos, lessons, and practice questions. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Also, if you’re looking to learn more about dividing polynomials, check out this post here!

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring Review

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Focus and Directrix of a Parabola

Quadratic Equations with 2 Imaginary Solutions

How to Construct an Equilateral Triangle?: Geometry

Advertisements

Happy Wednesday math peeps! This post introduces constructions by showing us how to construct an equilateral triangle by using a compass and straightedge (or ruler). For anyone new to constructions in geometry, this is the perfect topic for art aficionados since there is more drawing here than there is actual math!

What is an Equilateral Triangle?

Equilateral Triangle: An equilateral triangle is a triangle with three equal sides. Not an easy one to forget, the equilateral triangle is super easy to construct given the right tools (compass+ straightedge). Take a look below:

Equilateral Triangle: Triangle with all equal sides

Construct an Equilateral Triangle Example:

Check out the GIF below to see how to construct an equilateral triangle step by step using a compass and straightedge with pictures and explanations below!

Solution:

What’s Happening in this GIF?

1. Using a compass, we measure the distance of line segment .

2. With the compass point remaining on point A, we then draw an arc that has the same distance as line segment .

3. With the compass now placed on point B, draw an arc that has the same distance as line segment .

4. Notice where the arcs intersect? Using a ruler, connect points A and B to the new intersection point. This will create two new equal sides of our triangle!

5. We have now officially constructed a triangle with all equal side lengths!

Constructions and Related Posts:

Looking to construct more than just an equilateral triangle? Check out these related posts on geometry constructions!

Construct a Perpendicular Bisector

Perpendicular Line through a Point

Angle Bisector

Construct a 45º angle

Altitudes of a Triangle (Acute, Obtuse, Right)

Construct a Square inscribed in a Circle

Best Geometry Tools!

Still got questions? No problem! Don’t hesitate to comment with any questions. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking to learn more about triangles? Check out this post on right triangle trigonometry here! And if you’re looking for even more geometry constructions, check out the link here!

Expanding Cubed Binomials: Algebra 2/Trig.

Advertisements

Greetings math friends! This post will go over expanding cubed binomials using two different methods to get the same answer. We’re so used to seeing squared binomials such as, , and expanding them without a second thought. But what happens when our reliable squared binomials are now raised to the third power, such as,? Luckily for us, there is a Rule we can use:

But where did this rule come from? And how can we so blindly trust it? In this post we will prove why the above rule works for expanding cubed binomials using 2 different methods:

Why bother? Proving this rule will allow us to expand and simplify any cubic binomial given to us in the future! And since we are proving it 2 different ways, you can choose the method that best works for you.

Method #1: The Box Method

Step 1: First, focus on the left side of the equation by expanding (a+b)³:

Step 2: Now we are going to create our first box, multiplying (a+b)(a+b). Notice we put each term of (a+b) on either side of the box. Then multiplied each term where they meet.

Step 3: Combine like terms ab and ab, then add each term together to get a²+2ab+b².

Step 4: Multiply (a²+2ab+b²)(a+b) making a bigger box to include each term.

Step 5: Now combine like terms (2a²b and a²b) and (2ab² and ab²), then add each term together and get our answer: a³+3a²b+3ab²+b³.

Method #2: The Distribution Method

Let’s expand the cubed binomial using the distribution method step by step below:

Now that we’ve gone over 2 different methods of cubic binomial expansion, try the following practice questions on your own using your favorite method!

Practice Questions: Expand and simplify the following.

Solutions:

Still, got questions? No problem! Check out the video above or comment below! Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

**Bonus: Test your skills with this Regents question on Binomial Cubic Expansion!

Recursive Rule

Advertisements

Welcome to Mathsux! This post is going to show you everything you need to know about how to use a Recursive Formula by looking at three different examples of a recursive rule. Check out the video below for more of an explanation and test your skills with the practice questions at the bottom of this page. Please let me know if you have any questions in the comments section below and happy calculating! 🙂

What is a Recursive Formula or a Recursive Rule?

A Recursive Formula is a type of formula that forms a sequence based on the previous term value. The recursive rules for each formula vary, but we are always given the first term and a formula to find the consecutive terms in the recursive sequence.

Recursive formula can be written as an arithmetic sequence (a sequence where the same number is either added or subtracted to each subsequent term to form a pattern) and recursive formulas can also be written as arithmetic sequences (a sequence where the same number is either multiplied or divided to each subsequent term to form a pattern). We’ll go over an example of each but both types of recursive rules are treated the same exact way!

What does all of this mean? Check out the example below for a clearer picture.

Example #1: Arithmetic Recursive Sequence

Step 1: First, let’s decode what these formulas are saying.

Step 2: The first term, represented by a₁, is and will always be given to us. In this case, our first term has the value a₁=2 and represents the first term of our recursive sequence.

a₁= First Term=2

Step 3: We then plug in the value of our first term, which is a₁=2 into our formula a_n+4 to get 2+4=6. The number 6 now has the value of our second term in the recursive sequence.

a₁= 2 First Term

a₂= (2)+4=6 Second Term

Step 4: Now we are going to continue the pattern, plugging in the value of each previous term to find the next consecutive terms in our recursive sequence.

The pattern can be more easily seen below. Notice we are able to find the value of all 5 terms of the recursive sequence for the solution only given the first term and recursive formula at the beginning of our question.

Step 5: We found the recursive sequence we were looking for: 2, 6, 10, 14, 18. Since the question was originally only asking for the value of the fifth term we know our solution only needs to be the value of the fifth term which is 18.

Example #2: Geometric Recursive Sequence

Step 1: First, let’s decode what these formulas are saying.

Step 2: The first term, represented by a₁, is and will always be given to us. In this case, our first term has the value a₁=1 and represents the first term of our recursive sequence.

a₁= First Term=1

Step 3: We then plug in the value of our first term, which is a₁=1 into our formula 2^a_n+1 to get 2¹+1=3. The number 3 now has the value of our second term in the recursive sequence.

a₁= 1 First Term

a₂= 2⁽¹⁾+1=3 Second Term

Step 4: Now we are going to continue the pattern, plugging in the value of each previous term to find the next term in our recursive sequence.

The pattern can be more easily seen below. Notice we are able to find the value of all 3 terms of the recursive sequence for the solution only given the first term and recursive formula at the beginning of our question.

***Note this was written in a different notation but is solved in the exact same way! This recursive formula is a geometric sequence.

Step 5: We found the recursive sequence we were looking for: 1,3,9. Since the question was originally only asking for the value of the third term we know our solution only needs to be the value of the third term which is 9.

Example #3:

Step 1: First, let’s decode what these formulas are saying.

Step 2: The first term, represented by a₁, is and will always be given to us. In this case, our first term has the value a₁=4 and represents the first term of our recursive sequence.

a₁= First Term=4

Step 3: We then plug in the value of our first term, which is a₁=4 into our formula 3a_n-1-2 to get 3(2)-1=5. The number 5 now has the value of our second term in the recursive sequence.

a₁= 4 First Term

a₂= 3(2)-1=5 Second Term

Step 4: Now we are going to continue the pattern, plugging in the value of each previous term to find the next term in our recursive sequence.

Step 5: We found the recursive sequence we were looking for: 4,10,28. Since the question was originally only asking for the value of the third term we know our solution only needs to be the value of the third term which is 28.

Think you are ready to solve a recursive equation on your own?! Try finding the specific term in each given recursive function below:

Practice Questions:

Solutions:

Looking to learn more about sequences? You’ve come to the right place! Check out these sequence resources and posts below. Personally, I recommend looking at the arithmetic sequence or geometric sequence posts next!

Arithmetic Sequence

Geometric Sequence

Finite Arithmetic Series

Finite Geometric Series

Infinite Geometric Series

Golden Ratio in the Real World

Fibonacci Sequence

Still, got questions? No problem! Don’t hesitate to comment below or reach out via email. And if you would like to see more MathSux content, please help support us by following ad subscribing to one of our platforms. Thanks so much for stopping by and happy calculating!

Facebook ~ Twitter ~ TikTok ~ Youtube

***Bonus! Want to test yourself with a similar NYS Regents question on Recursive Formulas? Click here! And if you want to learn about even more sequences, check out the link here!

Reflections: Geometry

Advertisements

Greetings and welcome to Mathsux! Today we are going to go over reflections geometry, one of the many types of transformations that come up in geometry. And thankfully, reflection transformation is one of the easiest types to master, especially if you’re more of a visual learner/artistic type person. In this post, we will go over a reflection across the line x=-2, but if you want to see a reflection across the x axis, the y axis, and the line y=x, please check out the math video below! So let’s get to it! And if you’re new to transformations, check out translations here.

What are Reflections?

A Reflection on a coordinate plane is exactly what you think! A reflection is a type of transformation in geometry where we reflect a point, a line segment, or a shape over a line to create a mirror image of itself. Think of the wings of a butterfly, a page being folded in half, or anywhere else where there is perfect symmetry, each of these are great examples of a reflection!

Reflection Rules:

If you are completely new to reflections, you may want to check out the video above that goes into deriving reflection rules over the different axis. But for those of you more comfortable with reflection, check out the example below where we reflect the image of a triangle onto itself over the line x=-2.

Example:

Step 1: First, let’s draw in line x=-2. Note that whenever we have x equal to a number, we end up drawing a vertical line at that point on the x axis, in this case at x=-2.

Step 2: Find the distance each point is from the line x=-2 and reflect it on the other side, measuring the same distance.

First, let’s look at point C, notice it’s 1 unit away from the line x=-2 on the right. To reflect point c, we are going to count 1 unit but this time to the left of the line x=-2 and label our new point, C^|.

Step 3: Now we are going to reflect coordinate point A in much the same way! Notice that point A is 2 units away on the left of line x=-2, we then want to measure 2 units to the right of our line x=-2 and mark our new coordinate point, A^|.

Step 4: Lastly, we want to reflect coordinate point B. This time, point B is 1 unit away on the right side of the line x=-2, we then measure 1 unit to the opposite direction of our line, x=-2, and mark our new point, B^|.

Step 5: Now that we have all the newly reflected coordinate points of our triangle, finally, we can now connect them all, for our fully reflected image of right triangle A^|B^|C^|.

Notice our newly reflected triangle is not just a mirror image of itself, but when the original figure is reflected it actually ends up overlapping onto itself!? How did this happen? That is because this our reflection line came right down the middle of our original image, triangle ABC. Shapes that reflect onto themselves are a bit tricky but not impossible, just remember to measure out the distance of each coordinate point and reflections should be a breeze!

Rigid Motion:

Reflections are a special type of transformation in geometry that maintains rigid motion, meaning when a point, line, or shape is reflected the angles, and line segments retain their value. For example, if we were to measure the area of both right triangles, before and after reflection, we would find the areas to remain unchanged. Meaning the area of triangle ABC is equal to the area of triangle A^|B^|C^| . Another rigid transformation includes rotations and translations.

Looking to practice your new reflection skills? Try the reflection practice problems below, with solutions to each question, to truly master the topic! Happy calculating!

Practice Questions:

Solutions:

Still got questions? No problem! Check out the video above or comment below! There is also a bonus video if you scroll all the way down at the end of this post for anyone who wants to see how to reflect a line over the line x=2. See how it differs and how it is similar to the example shown here. Happy calculating! 🙂

Don’t forget to follow MathSux on social media for the latest tips and tricks to ace math!

Facebook ~ Twitter ~ TikTok ~ Youtube

And if you are looking for more Transformations Check out the related posts below and let me know if you have any questions? Or maybe you just want to share your favorite type of transformation? Either way, happy calculating!

Translations

Dilations

Rotation

Piecewise Functions: Algebra

Advertisements

Greetings, today’s post is for those in need of a piecewise functions review! This will cover how to graph each part of that oh so intimidating piecewise functions. There’s x’s, there are commas, there are inequalities, oh my! We’ll figure out what’s going on here and graph each part of the piecewise-function one step at a time. Then check yourself with the practice questions at the end of this post. Happy calculating! 🙂

What are Piece-Wise Functions?

Exactly what they sound like! A function that has multiple pieces or parts of a function. Notice our function below has different pieces/parts to it. There are different lines within, each with their own domain.

Now let’s look again at how to solve our example, solving step by step:

Translation: We are going to graph the line f(x)=x+1 for the domain where x > 0

To make sure all our x-values are greater than or equal to zero, we create a table plugging in x-values greater than or equal to zero into the first part of our function, x+1. Then plot the coordinate points x and y on our graph.

Translation: We are going to graph the line f(x)=x-3 for the domain where x < 0.

To make sure all our x-values are less than zero, let’s create a table plugging in negative x-values values leading up to zero into the second part of our function, x-3. Then plot the coordinate points x and y on our graph.

Ready to try the practice problems below on your own!?

Practice Questions:

Graph each piecewise function:

Solutions:

Still got questions? No problem! Check out the video above or comment below for any questions. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

***Bonus! Want to test yourself with a similar NYS Regents question on piecewise functions? Click here.

Intersecting Secants Theorem: Geometry

Advertisements

Ahoy! Today we’re going to cover the Intersecting Secants Theorem! If you forgot what a secant is in the first place, don’t worry because all it is a line that goes through a circle. Not so scary right? I was never scared of lines that go through circles before, no reason to start now.

If you have any questions about anything here, don’t hesitate to comment below and check out my video for more of an explanation. Stay positive math peeps and happy calculating! 🙂

Wait, what are Secants?

Intersecting Secants Theorem: When secants intersect an amazing thing happens! Their line segments are in proportion, meaning we can use something called the Intersecting Secants Theorem to find missing line segments. Check it out below:

Let’s now see how we can apply the intersecting Secants Theorem to find missing length.

Step 1: First, let’s write our formula for Intersecting Secants.

Step 2: Now fill in our formulas with the given values and simplify.

Step 3: All we have to do now is solve for x! I use the product.sum method here, but choose the factoring method that best works for you!

Step 4: Since we have to reject one of our answers, that leaves us with our one and only solution x=2.

Ready to try the practice problems below on your own!?

Practice Questions: Find the value of the missing line segments x.

Solutions:

Still got questions? No problem! Check out the video above or comment below for any questions and follow for the latest MathSux posts. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

To review a similar NYS Regents question check out this post here.

Circle Theorems & Formulas

Central Angle Theorem

Inscribed Angles & Intercepted Arcs

Area of a Sector

Circle Theorems

Absolute Value Equations: Algebra

Advertisements

Happy Wednesday math friends! Today, we’re going to go over how to solve absolute value equations. Solving for absolute value equations supplies us with the magic of two potential answers since absolute value is measured by the distance from zero. And if this sounds confusing, fear not, because everything is explained below!

Also, if you have any questions about anything here, don’t hesitate to comment. Happy calculating! 🙂

Absolute Value measures the “absolute value” or absolute distance from zero. For example, the absolute value of 4 is 4 and the absolute value of -4 is also 4. Take a look at the number line below for a clearer picture: