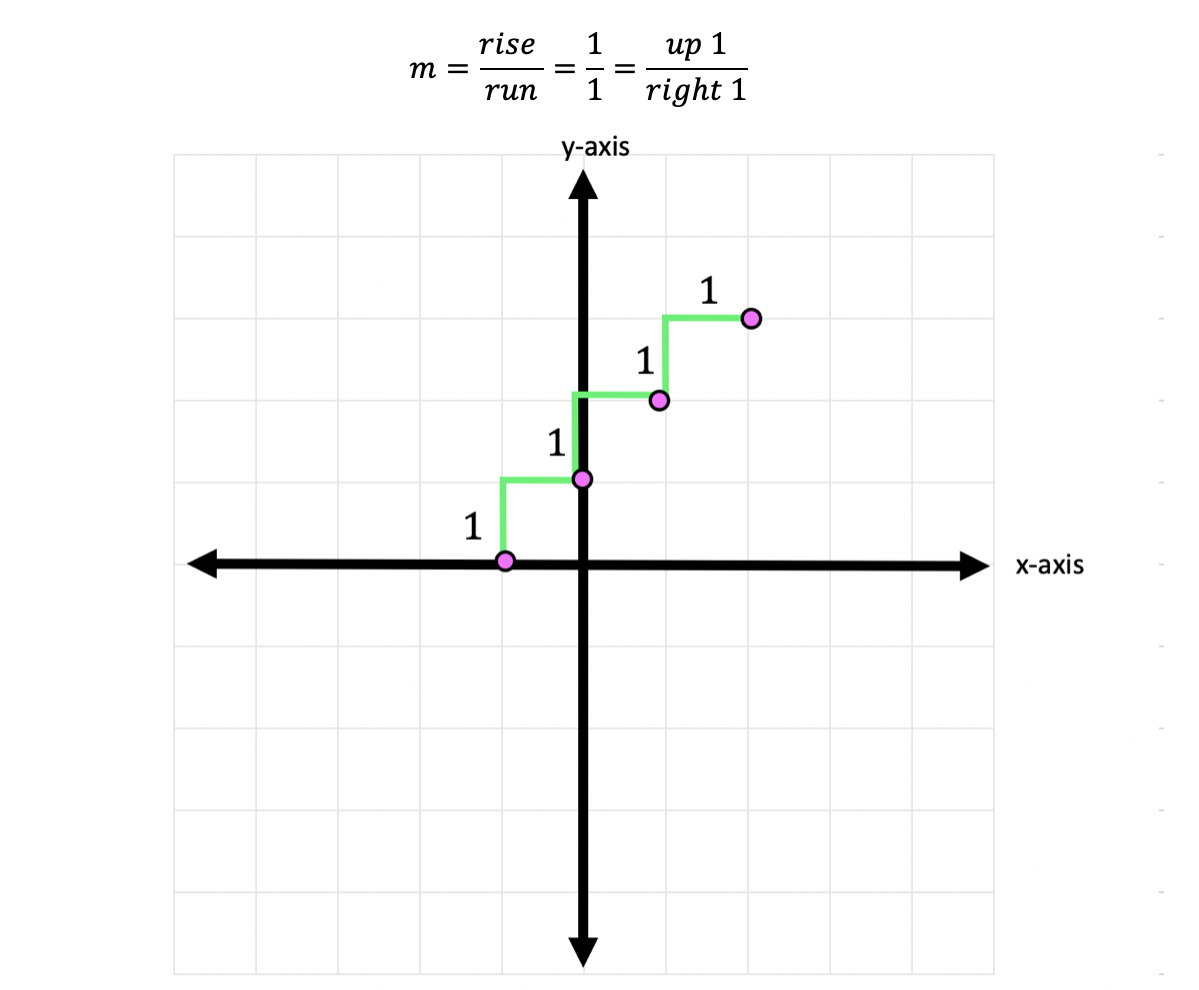
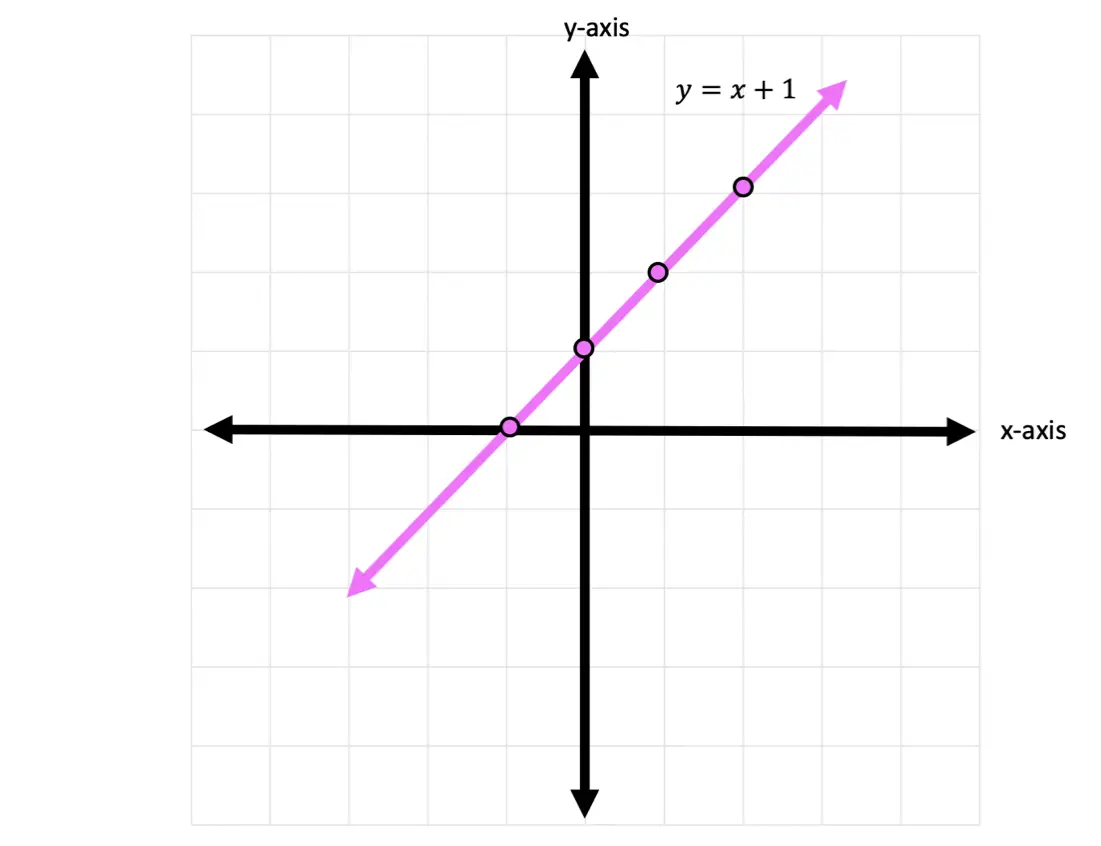
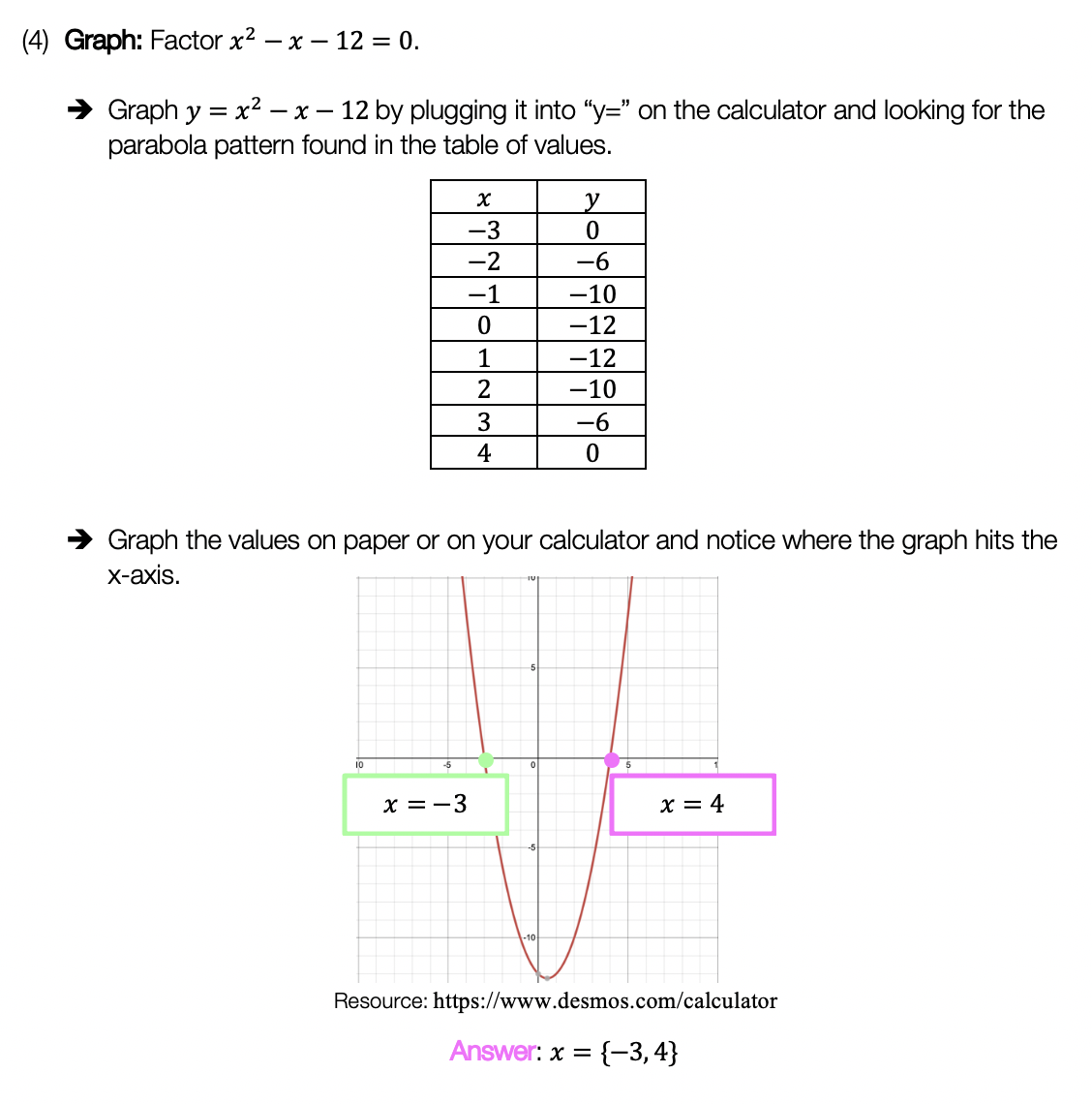
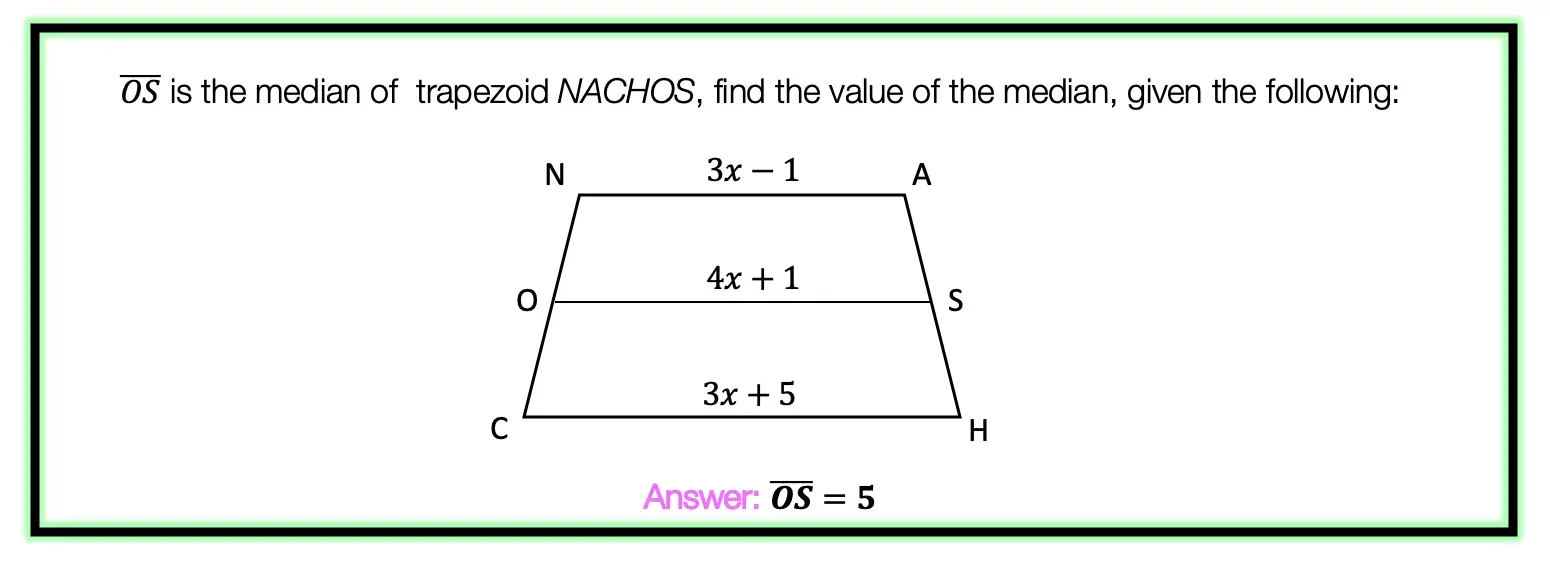
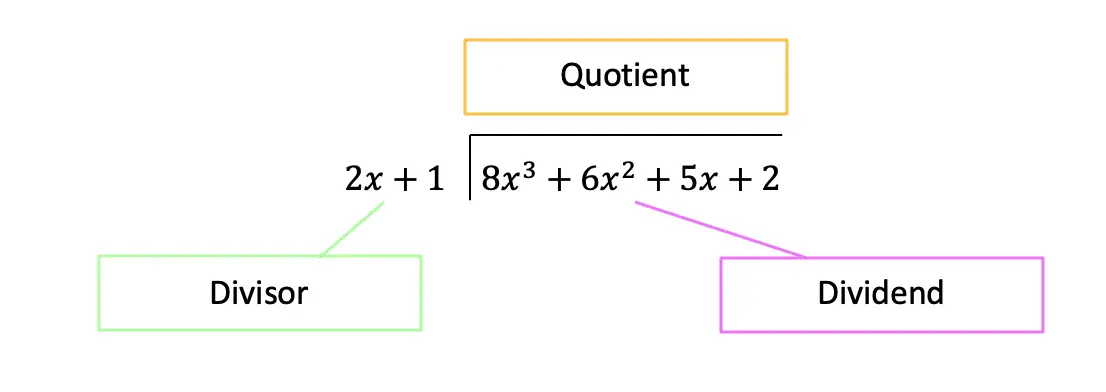
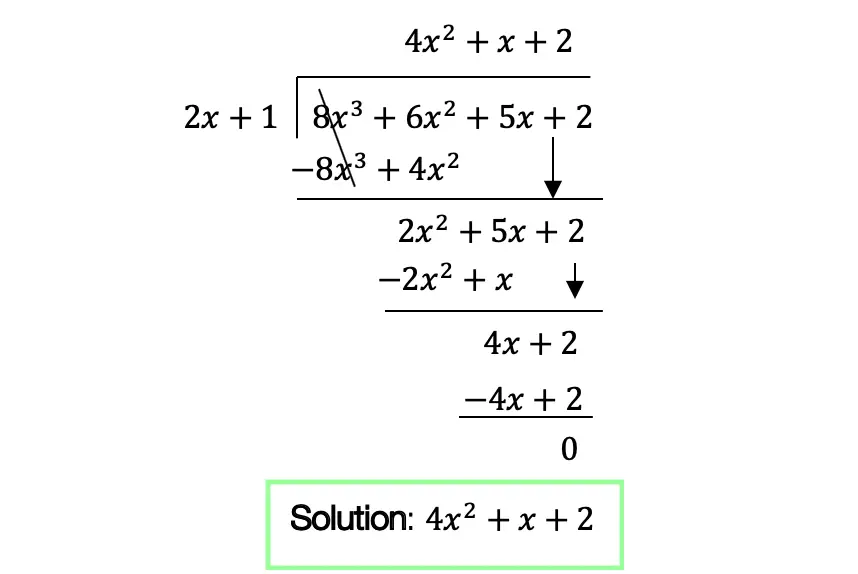
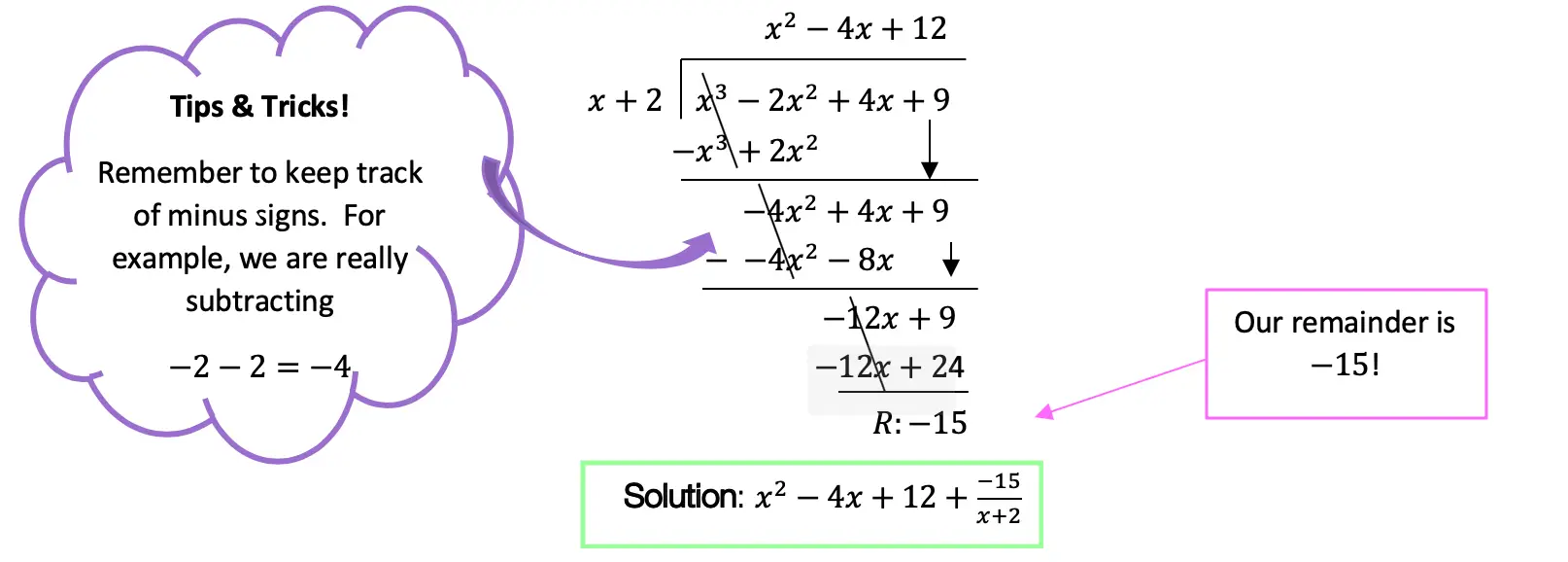
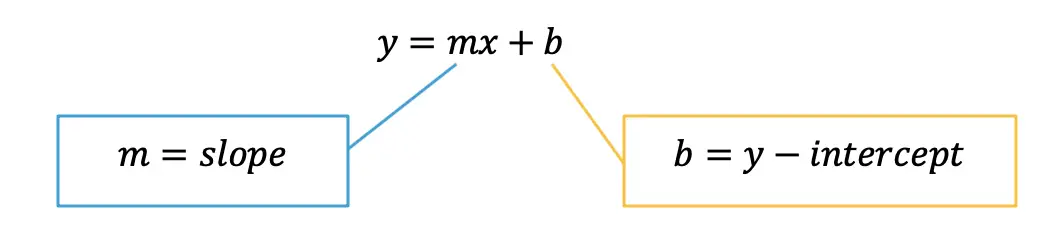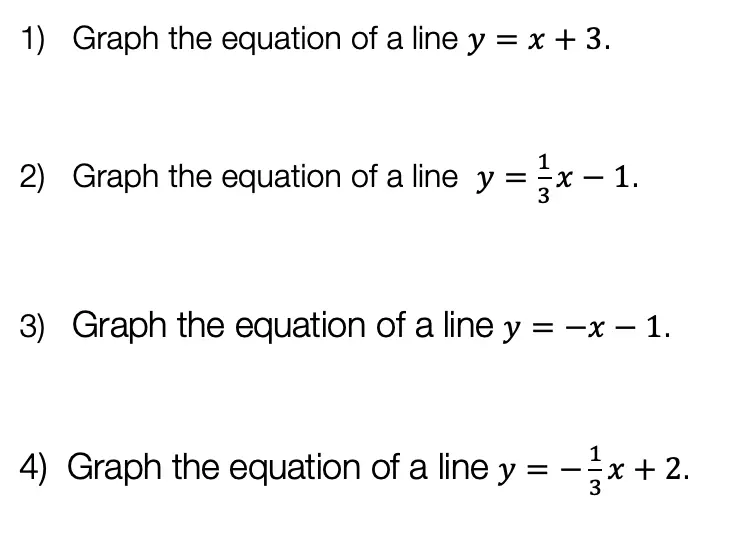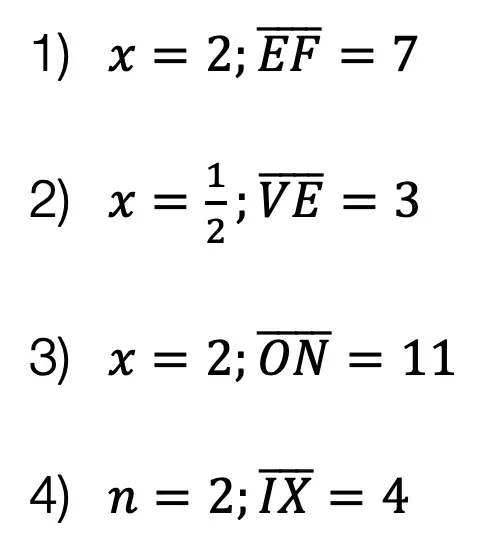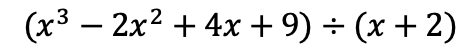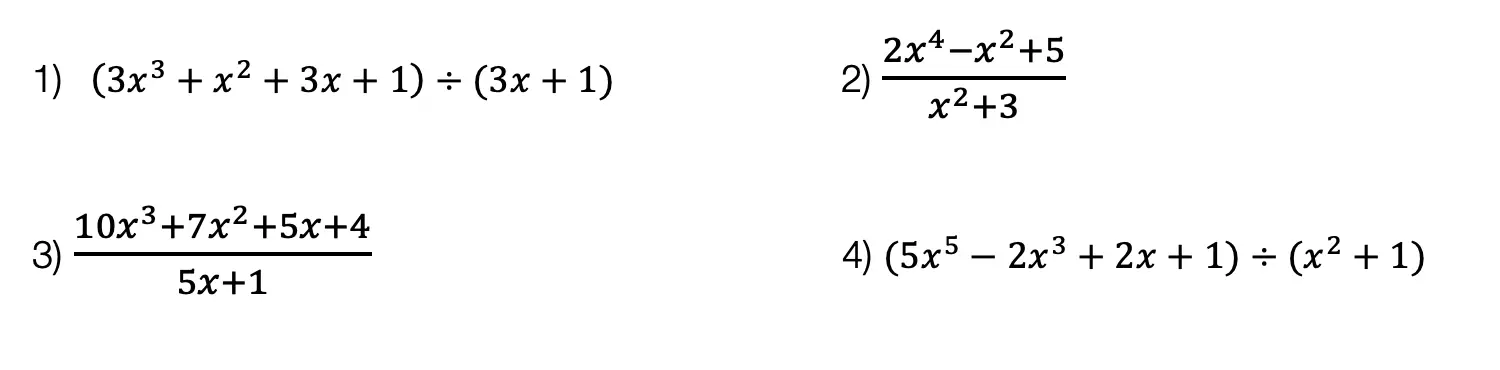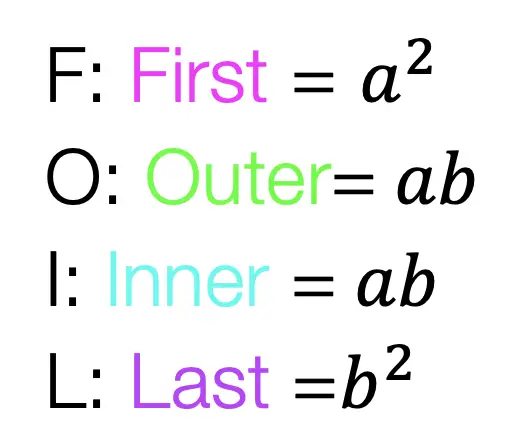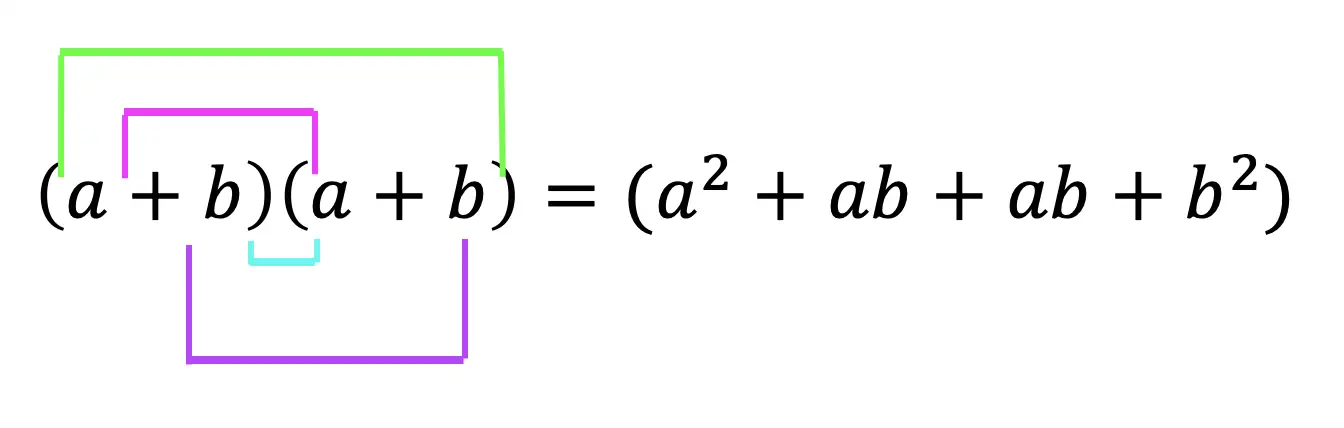Greetings math friends! This post will go over expanding cubed binomials using two different methods to get the same answer. We’re so used to seeing squared binomials such as, ![]() , and expanding them without a second thought. But what happens when our reliable squared binomials are now raised to the third power, such as,
, and expanding them without a second thought. But what happens when our reliable squared binomials are now raised to the third power, such as,![]() ? Luckily for us, there is a Rule we can use:
? Luckily for us, there is a Rule we can use:
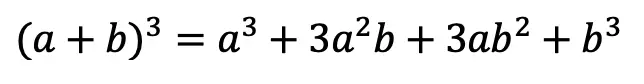
But where did this rule come from? And how can we so blindly trust it? In this post we will prove why the above rule works for expanding cubed binomials using 2 different methods:

Why bother? Proving this rule will allow us to expand and simplify any cubic binomial given to us in the future! And since we are proving it 2 different ways, you can choose the method that best works for you.
Method #1: The Box Method
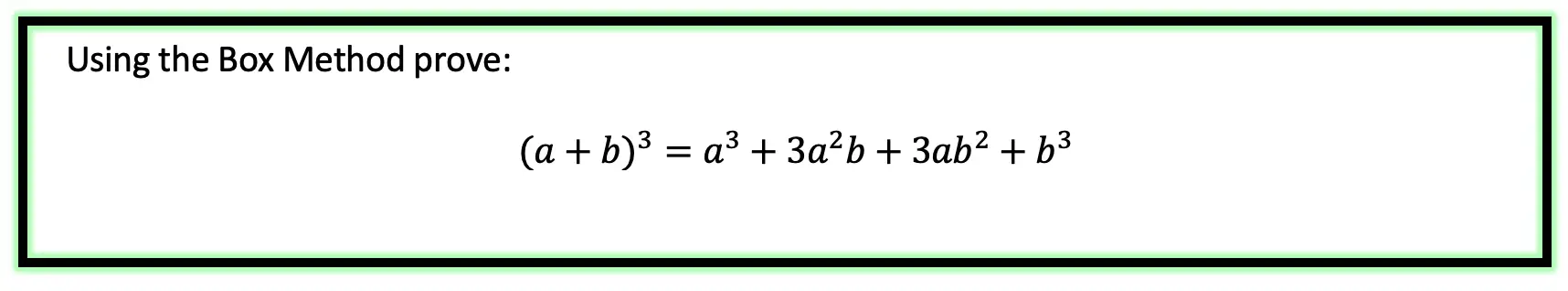
Step 1: First, focus on the left side of the equation by expanding (a+b)3:
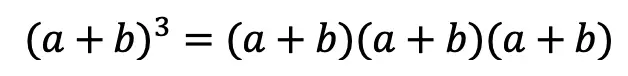
Step 2: Now we are going to create our first box, multiplying (a+b)(a+b). Notice we put each term of (a+b) on either side of the box. Then multiplied each term where they meet.
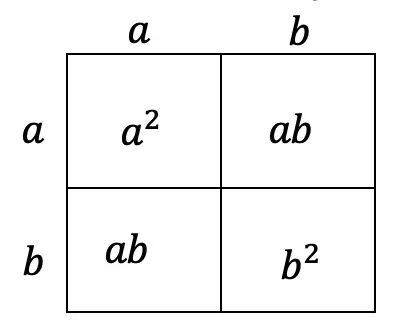
Step 3: Combine like terms ab and ab, then add each term together to get a2+2ab+b2.
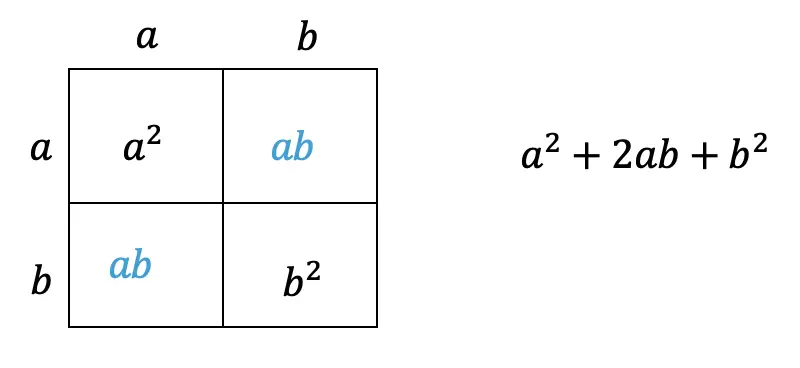
Step 4: Multiply (a2+2ab+b2)(a+b) making a bigger box to include each term.
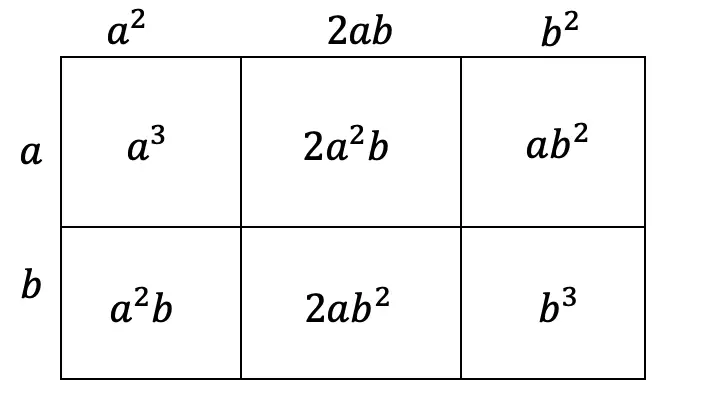
Step 5: Now combine like terms (2a2b and a2b) and (2ab2 and ab2), then add each term together and get our answer: a3+3a2b+3ab2+b3.
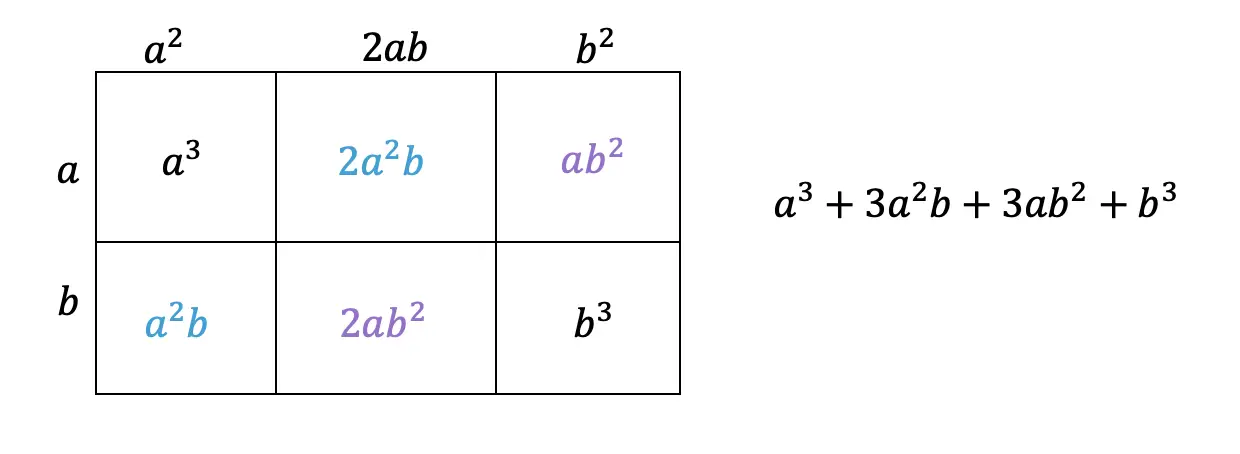
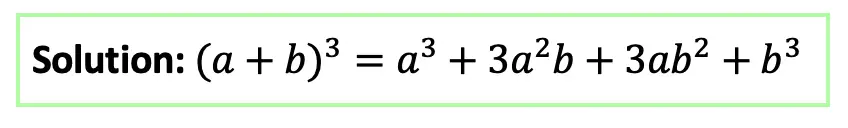
Method #2: The Distribution Method
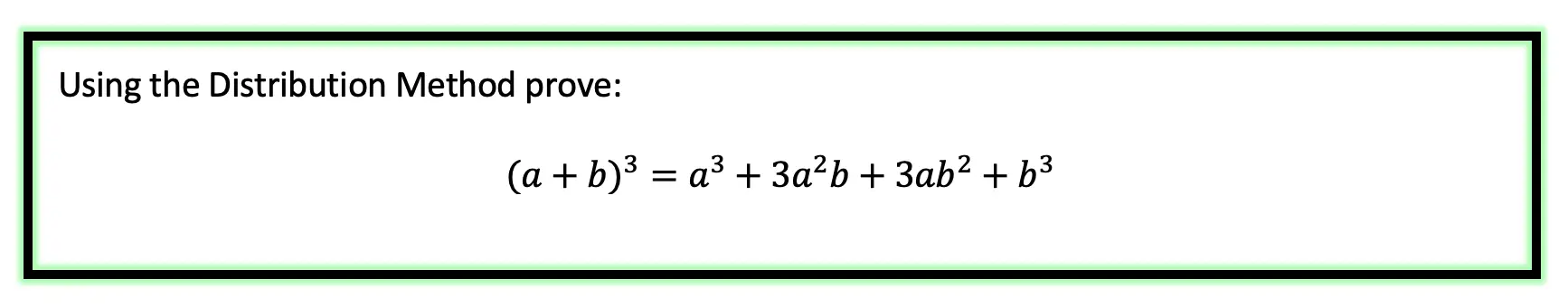
Let’s expand the cubed binomial using the distribution method step by step below:

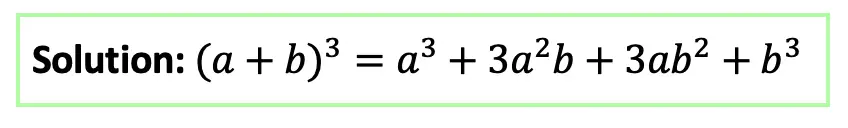
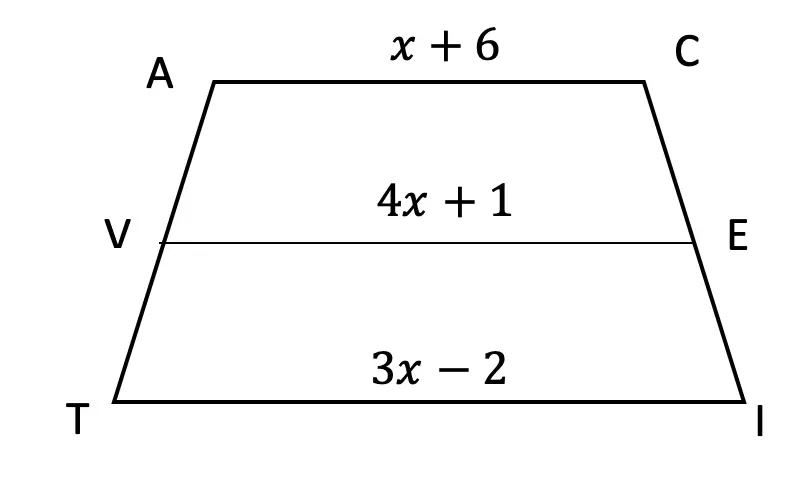
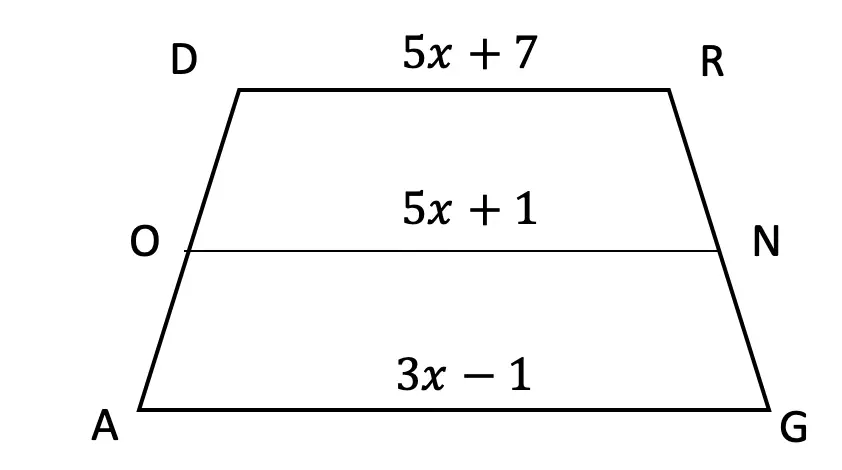
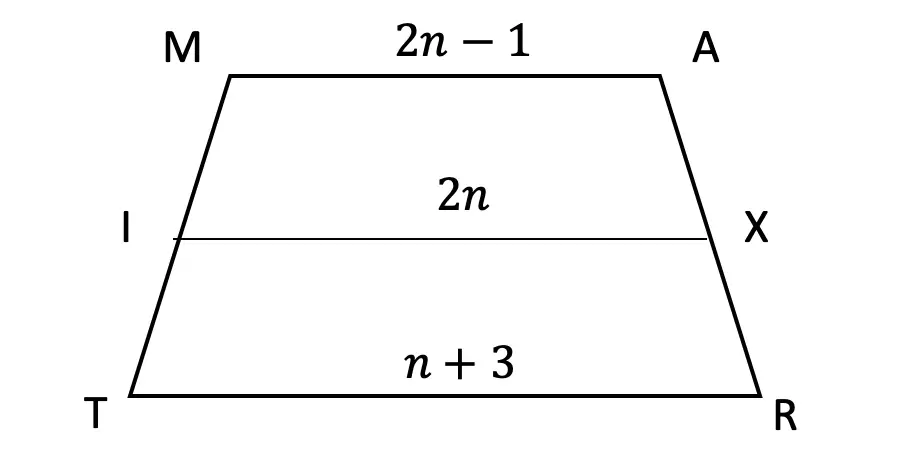
Now that we’ve gone over 2 different methods of cubic binomial expansion, try the following practice questions on your own using your favorite method!
Practice Questions: Expand and simplify the following.

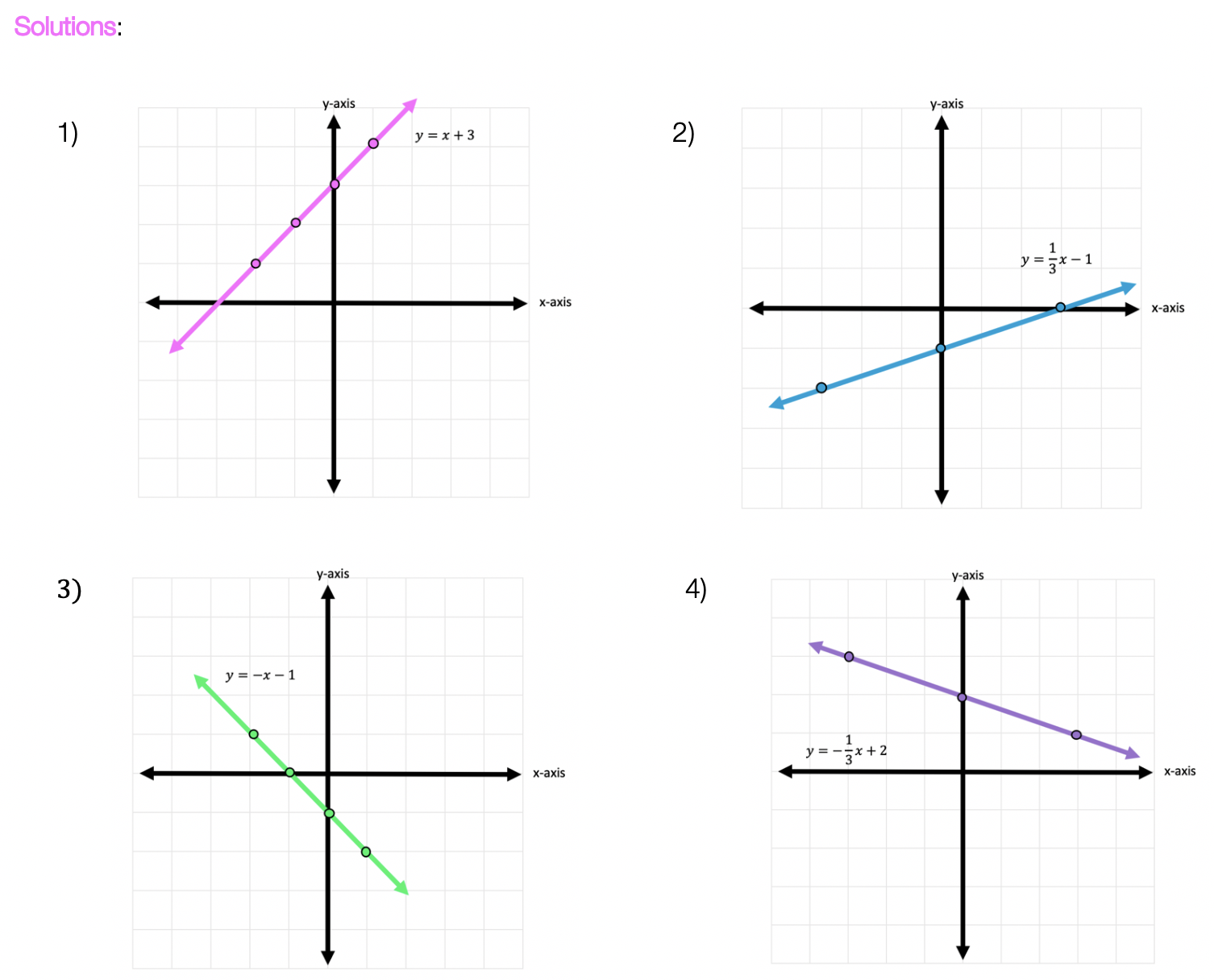
Solutions:
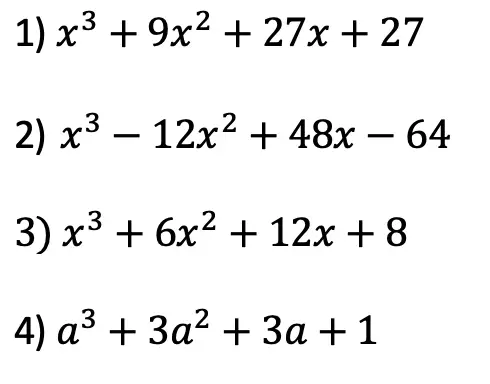
Still, got questions? No problem! Check out the video above or comment below! Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
**Bonus: Test your skills with this Regents question on Binomial Cubic Expansion!