Hi everyone and welcome to MathSux! In today’s post we are going to be solving quadratic equations by using the quadratic formula. You may have used the quadratic formula before, but this time we are working with quadratic equations with two imaginary solutions. All this means is that there are negative numbers under the radical that have to be converted into imaginary numbers. If you need a review on imaginary numbers or the quadratic formula before reading this post, check out these links! Thanks so much for stopping by and happy calculating! 🙂
What is the Quadratic Formula?
The Quadratic formula is a formula we use to find the x-values of a quadratic equation. When we find the x-value of a quadratic equation, we are actually finding its x-values on the coordinate plane. Check out the formula below:
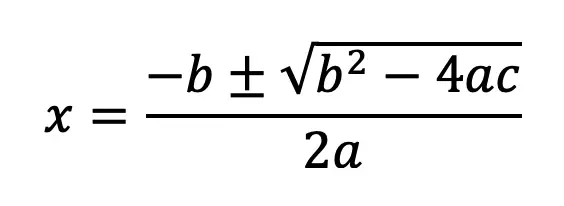
where, a, b, and c are coefficients based on the quadratic equation in standard form:
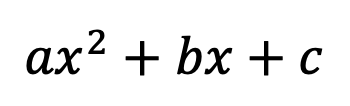
What does it mean to have “Imaginary Roots”?
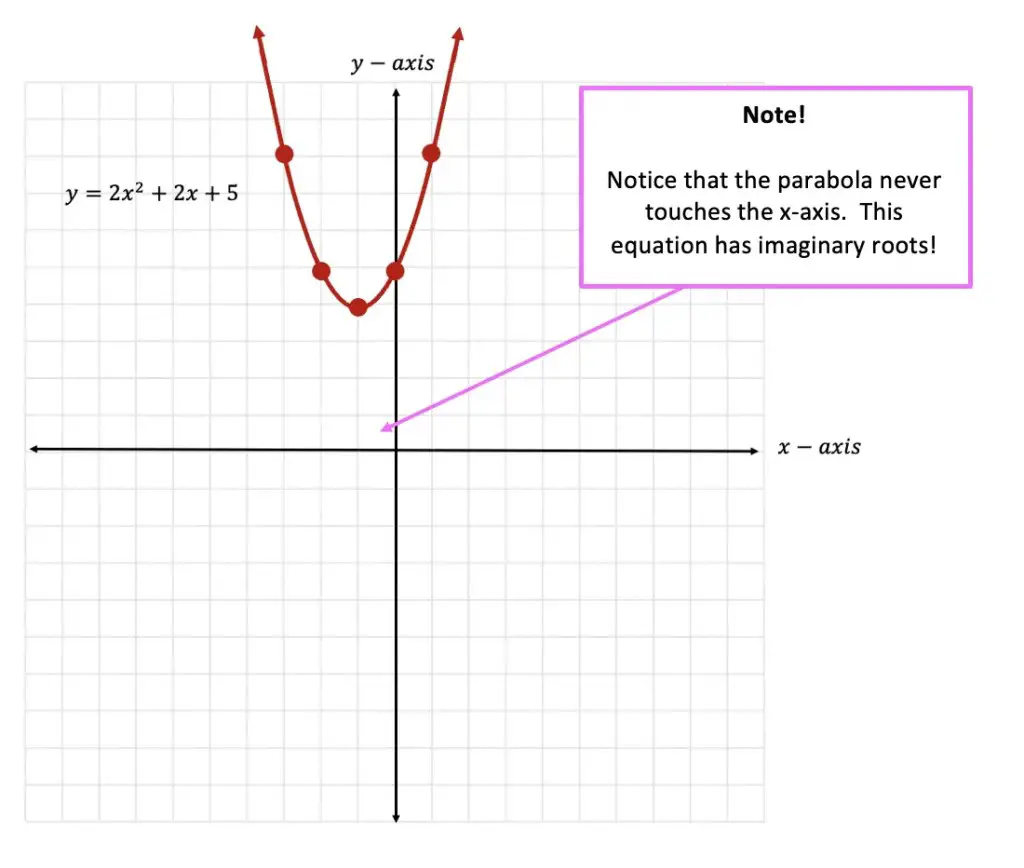
When we solve for the x-values of a quadratic equation, we are always looking for where the equation “hits” the x-axis. But when we have imaginary numbers as roots, the quadratic equation in question, never actually hit the x-axis. Ever. This creates a sort of “floating” quadratic equation with complex numbers as roots. See what it can look like below:
Ready for an Example? Let us see how to use the quadratic formula specifically, quadratic equations with two imaginary solutions:
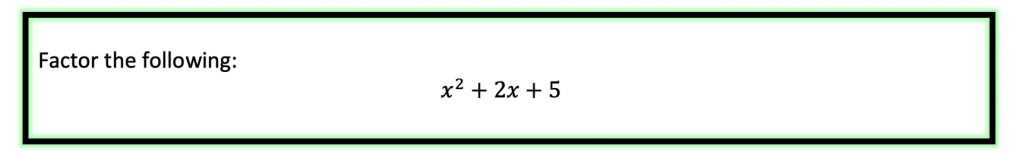

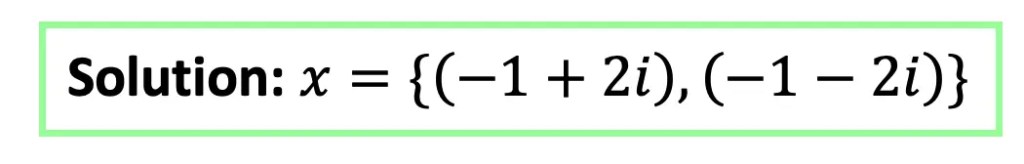
Think you are ready to try practice questions on your own? Check out the ones below!
Practice Questions:
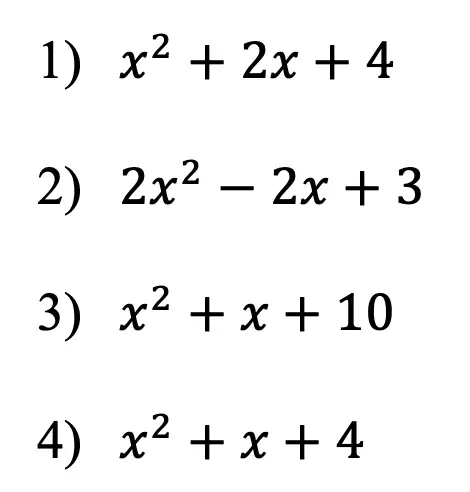
Solutions:
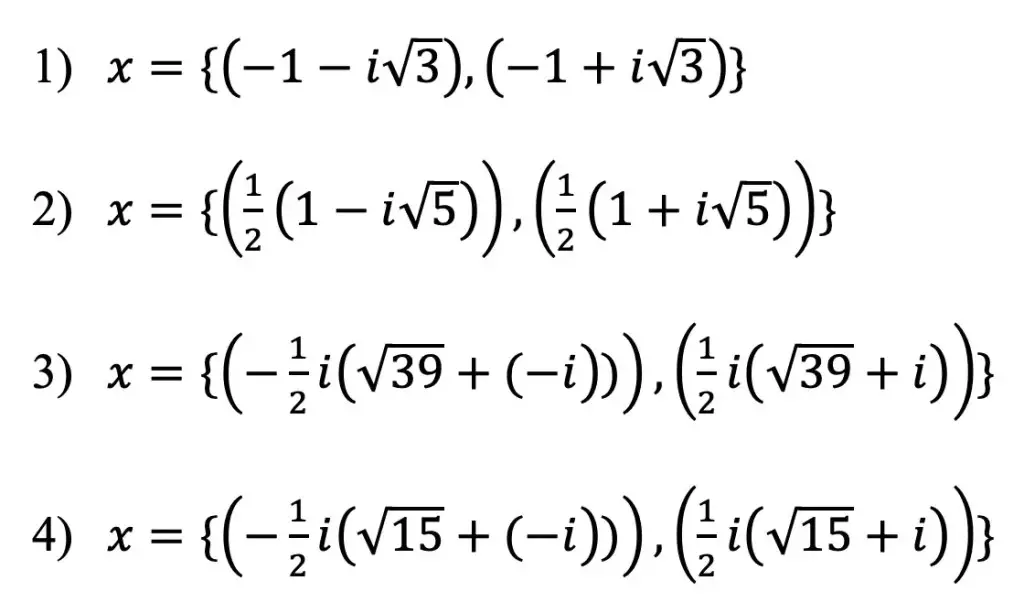
Still got questions? No problem! Don’t hesitate to comment with any questions below or check out the video above. Thanks for stopping by and happy calculating! 🙂

This is so good. I know this type of content takes lot of time to create. Wonderful work. Thank you. Sharing.
Thank you, really appreciate it!