Hi everyone and welcome to MathSux! In this post, we are going to answer the question, what is the discriminant? Before going any further, if you need a review on what the quadratic equation or imaginary numbers are, check out each related link! Also, don’t forget to check out the video and practice questions below. Happy calculating! 🙂
What is the Discriminant?
The discriminant is a formula we can use that tells us more about a quadratic equation including:
- The number of solutions a quadratic equation has.
- The “nature” of the roots of the solution (rational/irrational or real/imaginary).
Discriminant Formula:
The discriminant formula may look familiar! It is part of the quadratic formula and we have seen it before, using the very same coefficients a, b, and c from the quadratic equation.

How does it Work?
When we find the value of the discriminant of any quadratic equation, it will give us a value that tells us how many solutions (or roots) a quadratic equation has. Remember when we say “roots” what we really mean are the x-value(s) of the quadratic equation that hit the x-axis. This value will also tell us if the solutions to the quadratic equation are rational/irrational or real/imaginary. Take a look at how it all breaks down below:
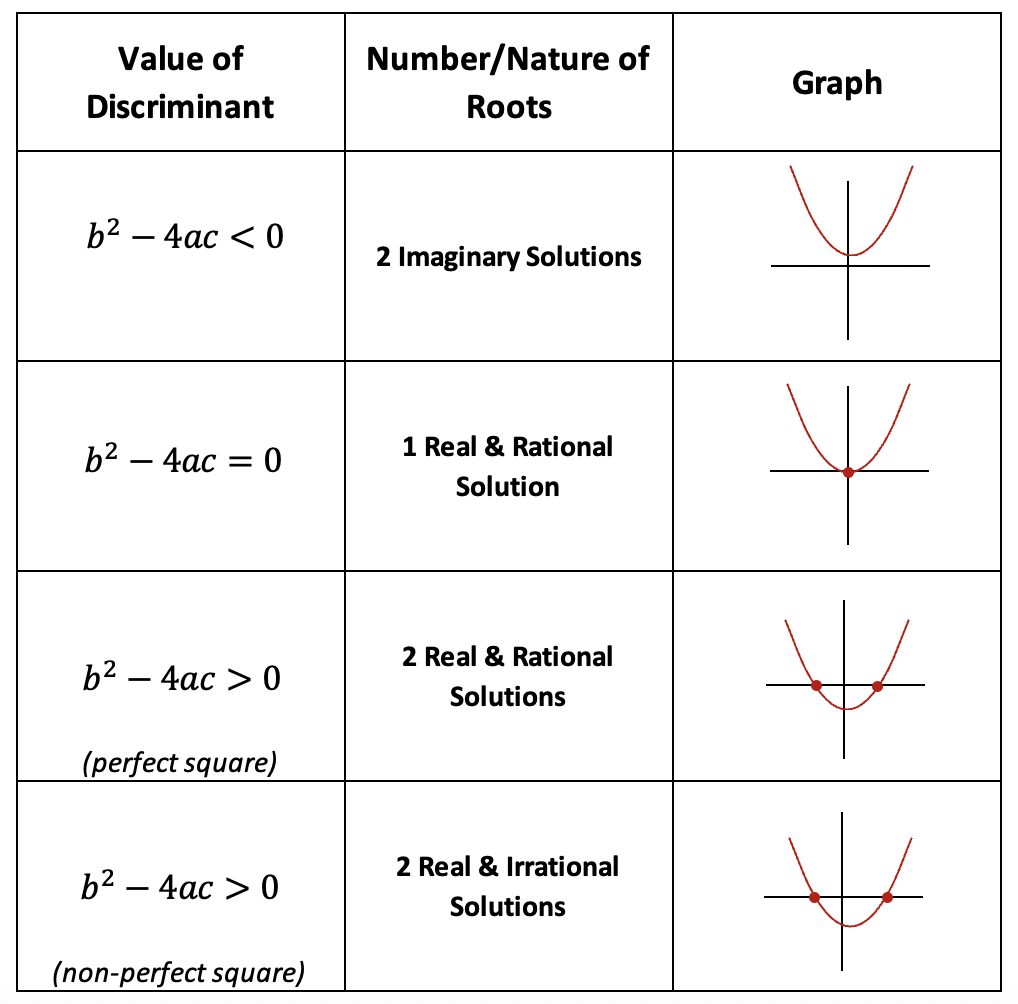
Now that we are familiar with the rules, let’s take a look at an Example:

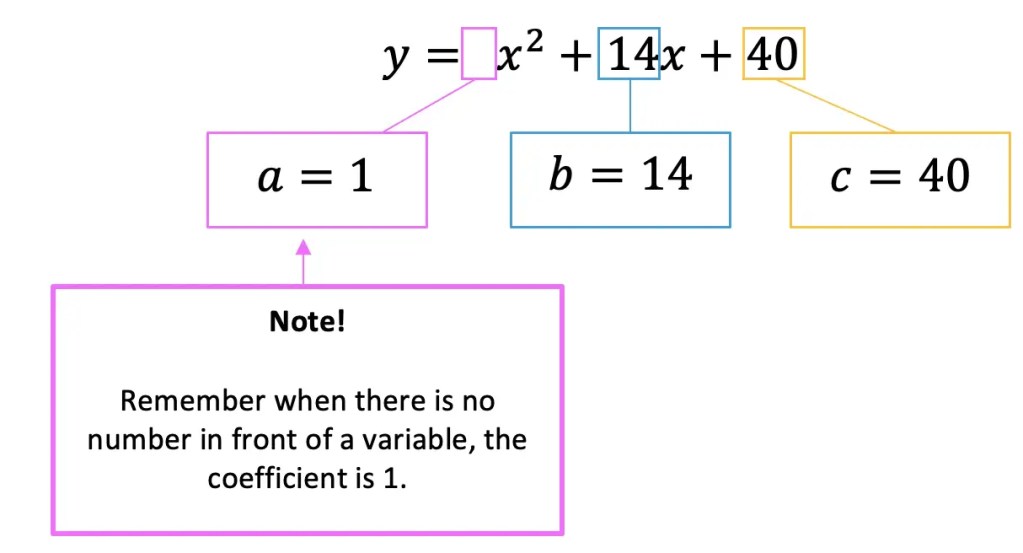
Step 1: First let’s write out our quadratic equation and identify the coefficients a, b, and c so they are ready to be plugged into our discriminant formula.
Step 2: Now let’s write out and fill in our formula using the coefficients and solve.
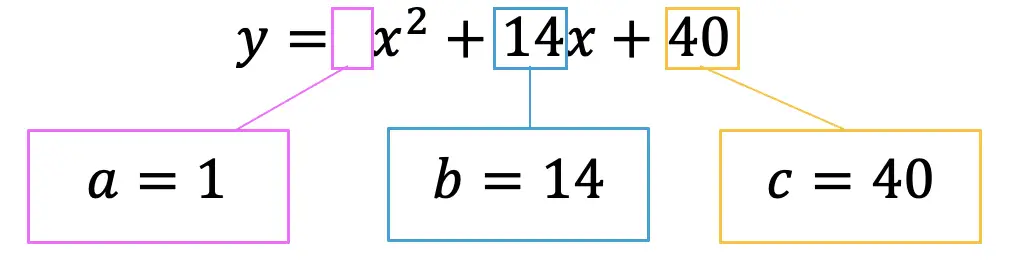

Step 3: Now let’s analyze our answer! Since, we got a discriminant value of 36, notice that it is a positive perfect square! If we look back at our discriminant table, this tells us that our quadratic equation is going to have 2 real and rational solutions.

Practice Questions:
Find the discriminant, number of solutions and nature of the roots of the following quadratic equations:
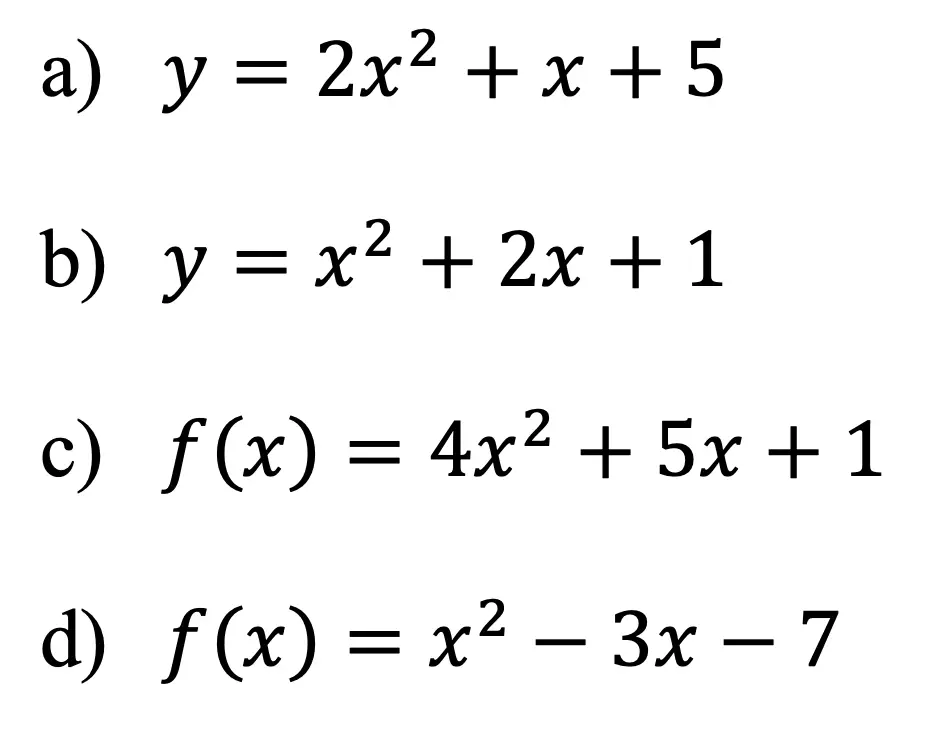
Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions below or check out the video above. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Looking for more on Quadratic Equations and Functions? Check out the following Related posts!

2 thoughts on “What is the Discriminant?”