In this post, we are going to dive deep into how to factor Quadratic equations! There are so many different methods to choose from including GCF, Product/Sum, DOTS, and the Quadratic Formula. Here we will go step by step into each method on how to factor quadratic equations, each with their own set of practice questions. For a review on how to factor by grouping, check out this post here and happy calculating! 🙂
Why factor in the first place, you may say? We want to manipulate the equation until we solve for x. Solving for x is our main goal, and factoring allows us to do that. Now let’s get to the good stuff!

Greatest Common Factor (GCF):
The greatest common factor is the highest possible number that can be divided out from an equation. This gets the equation into its simplest form and makes it easier for us to solve for x.
Before considering which type of factoring methdo to use, always ask yourself, “Can I take out a GCF?”
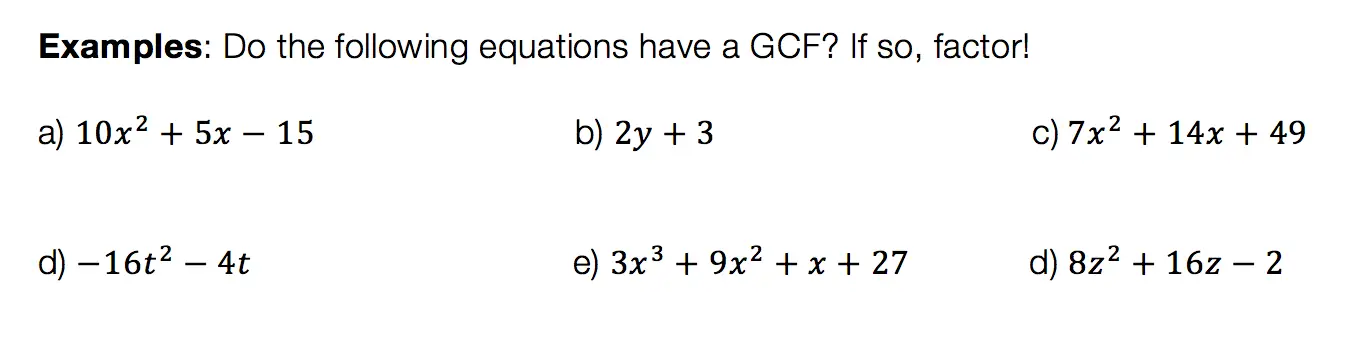
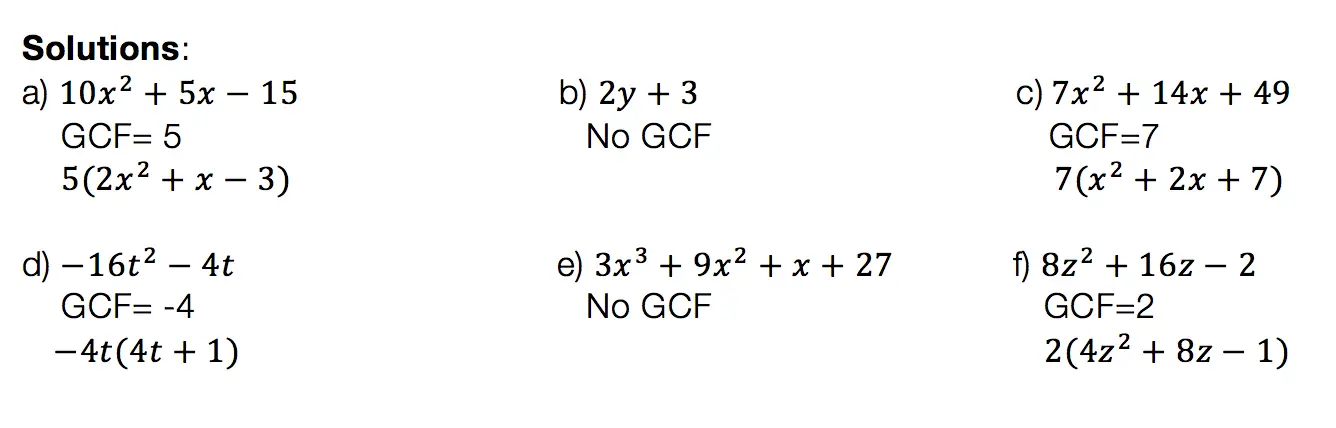

Product/Sum:
This factoring method is for quadratic equations only! That means the equation takes on the following form:
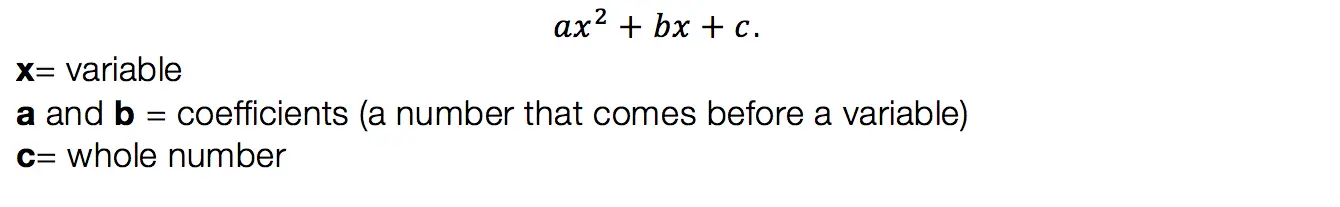
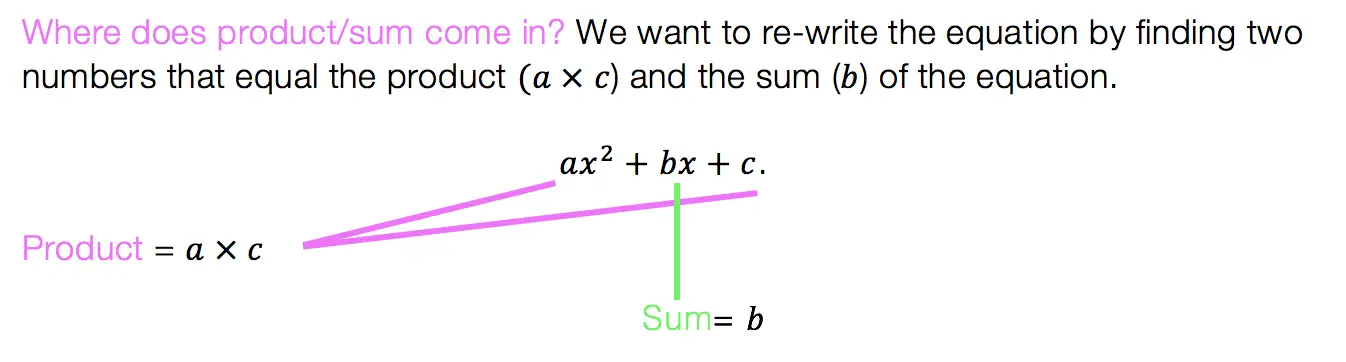
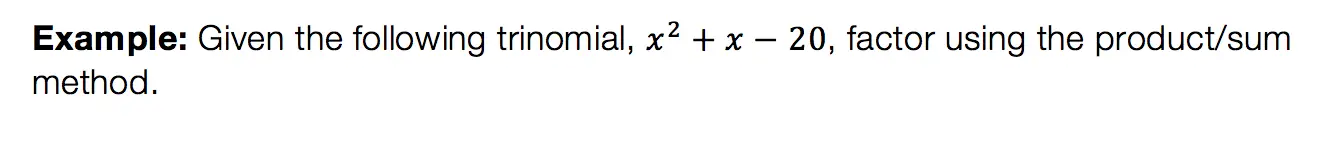
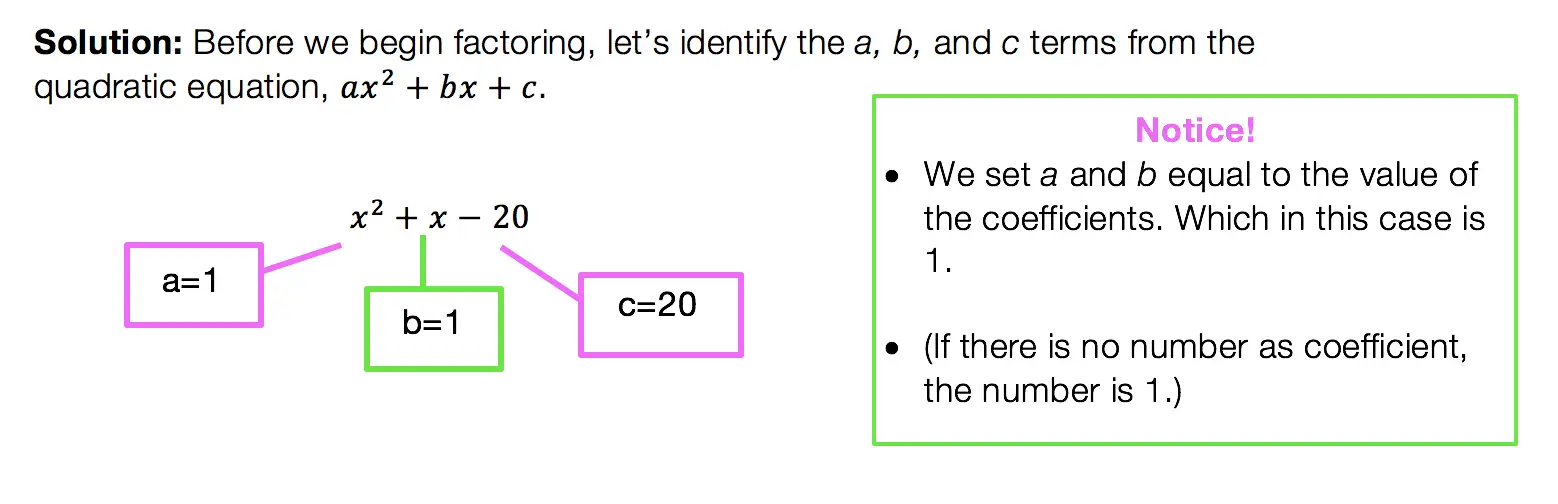

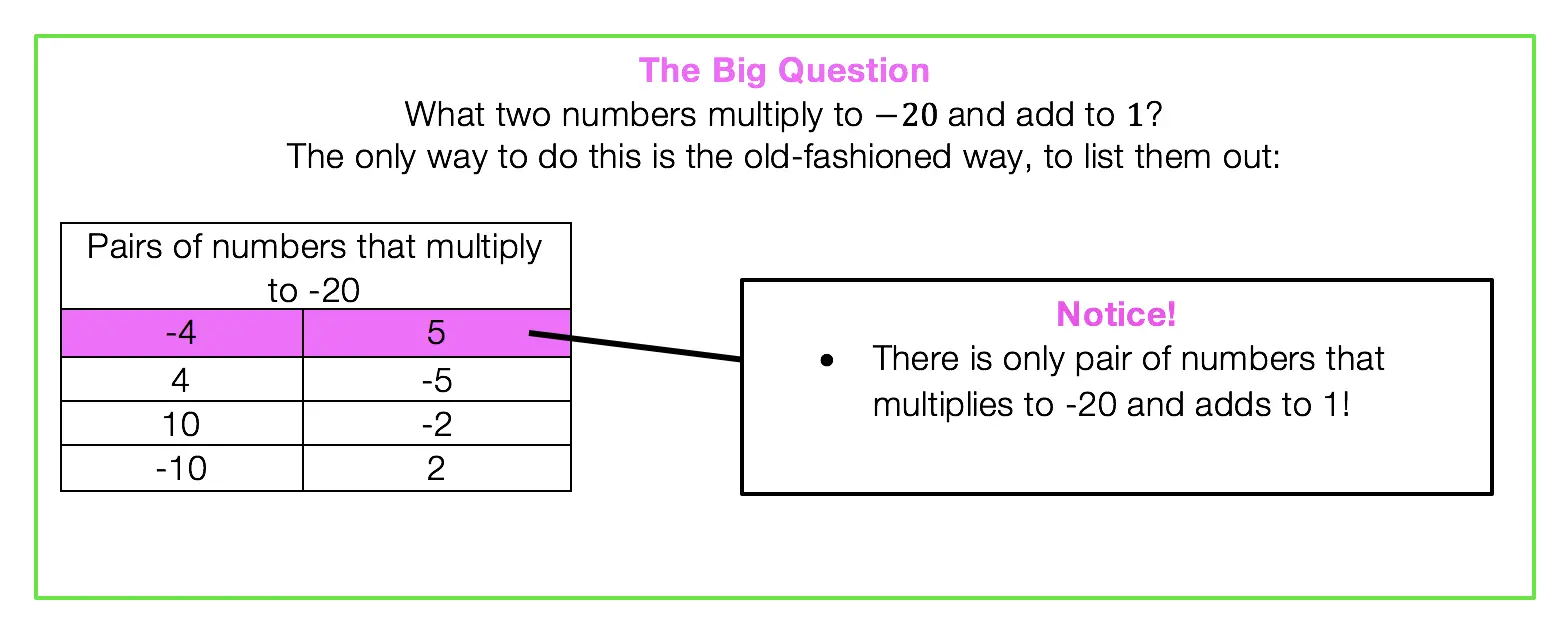



Difference of Two Squares DOTS)
Not to play favorites or anything, but DOTS is the easiest and most lovable of the factoring methods. This factoring method just makes you feel all warm and fuzzy inside or maybe that’s just me). Before we get into how to do DOTS, let’s talk about when?


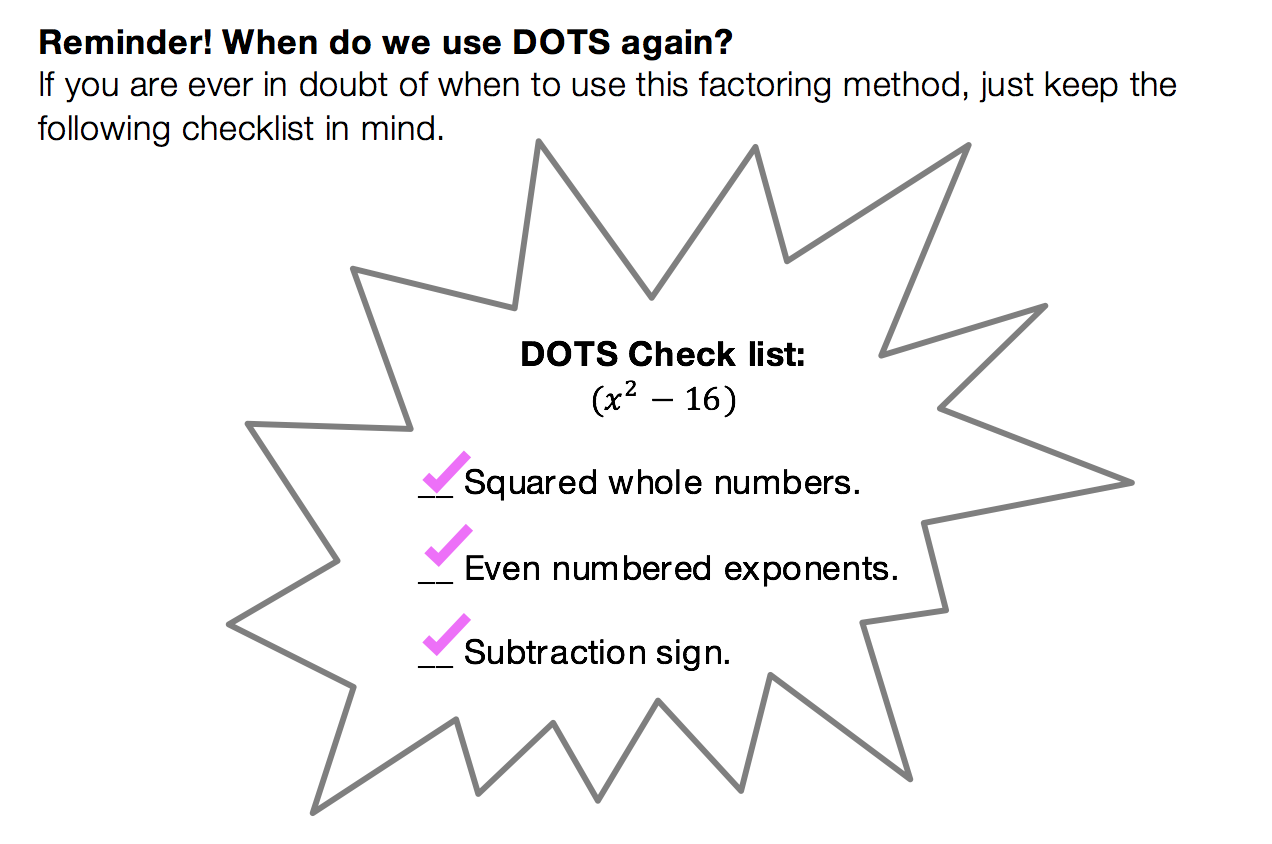
Quadratic Formula:
We have heard of the quadratic equations, so how id the quadratic formula different?
The Answer: The Quadratic Formula is what we use to factor any trinomial. You can use product/sum on trinomials like we discussed earlier, but this may not always work out easy. The Quadratic Formila on the other hand will work every time!
Low and behold, the Quadratic Formula:
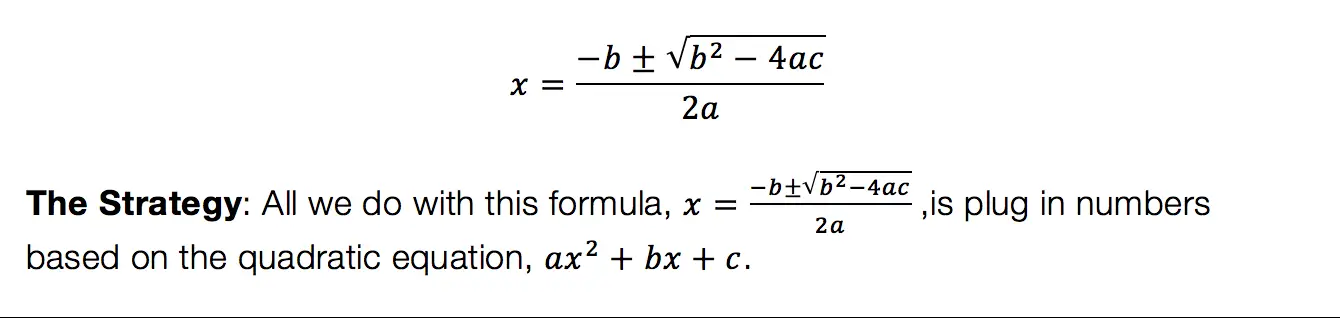

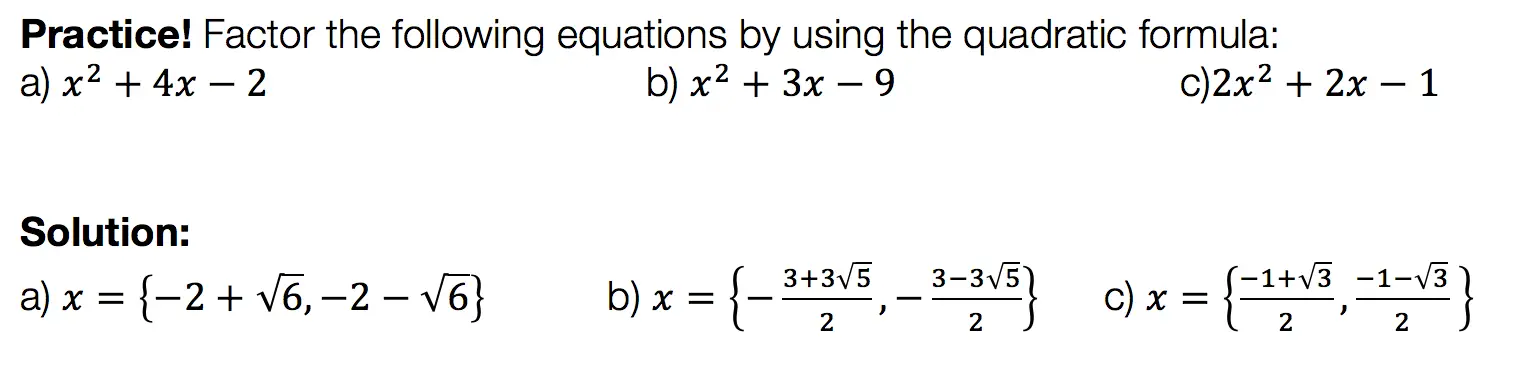
Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂
Looking for more on Quadratic Equations and functions? Check out the following Related posts!Quadratic Equations with 2 Imaginary Solutions

5 thoughts on “How to Factor Quadratic Equations: Algebra”