Greeting math peeps! Welcome to another MathSux post! Today we will be tackling how to find the missing lengths of medians on a trapezoid. We’ll do this by going over a question taken straight from the NYS Regents from August 2012. I must admit, that when I first looked at this question, I had no idea how to answer it! None. Zero. Clueless (also a great movie). But apparently, there is an explanation! And apparently it’s not so hard; you just have to know what to do.Let’s take a look:
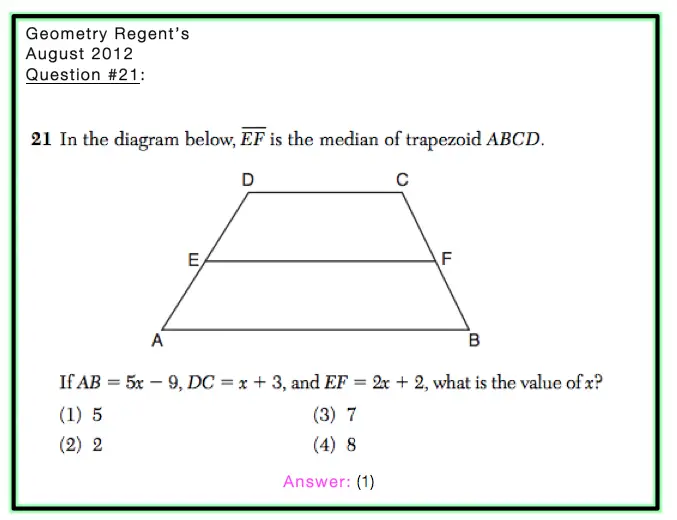
How do I answer this Question?
Step 1: Let’s fill in what we know, They tell us in the questions that AB=5x-9, DC=x+3, and EF=2x+2. So let’s write that in:
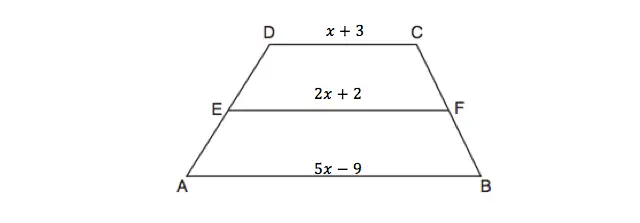
Ok, great what now? (This is where I got lost too). But wait! There is this amazing rule about medians on a trapezoid you probably didn’t know about (Exciting I know).

Step 2: Apply the rule and solve for x.
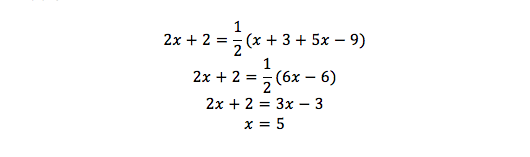
Answer: x=5
Yay! This gives us our answer 🙂 Another random rule in Geometry accomplished.
Still got questions? That’s cool, take a deep breath and ask me in the comments section.
Looking for more on Medians of a trapezoid? Check out this post here for practice questions and more!
Facebook ~ Twitter ~ TikTok ~ Youtube

To be honest, I never learned this in my high school (in Ontario, Canada). We had up to grade 13 in high school and Geometry before I entered high school. At my time they took out grade 13 and Geometry.
So this is why this is new to me. I think Geometry should make a comeback to increase demand for good architects to make fancy looking buildings/houses/theme parks, etc.
Now I know this. Thank you.
I took geometry in highschool but don’t even remember this. There are so many things to remember in this subject and if you don’t use it on a daily basis it’s so easy to forget. Glad you enjoyed this post! 🙂
I didn’t know the result you used. Here is how I thought about it:
Say EF is longer than DC by some amount L.
Notice that AB is longer than EF by the same amount L.
(You can see this by drawing triangles – draw lines straight down from C,D,E and F.)
This gives us:
2x+2=x+3+L,
5x-9=2x+2+L.
Taking the first equation from the second gives:
3x-11=x-1.
Now we can solve for x.
I never would have thought of that…that’s awesome! It makes a lot more sense than a random rule too. 🙂