Happy Wednesday math friends! In today’s post are going to go over what the focus and directrix of a parabola are and how to find them. We will also take a look at how to find the equation of a parabola when given the focus and directrix. You may already be familiar with parabolas and quadratic equations, but with this post we will dive deeper into the definition of a parabola and understand it on a whole new level! Don’t forget to check out the video and practice questions, below. Thanks for stopping by and happy calculating! 🙂
Parabola? Vertex? Focus? Directrix? What does it all mean?!
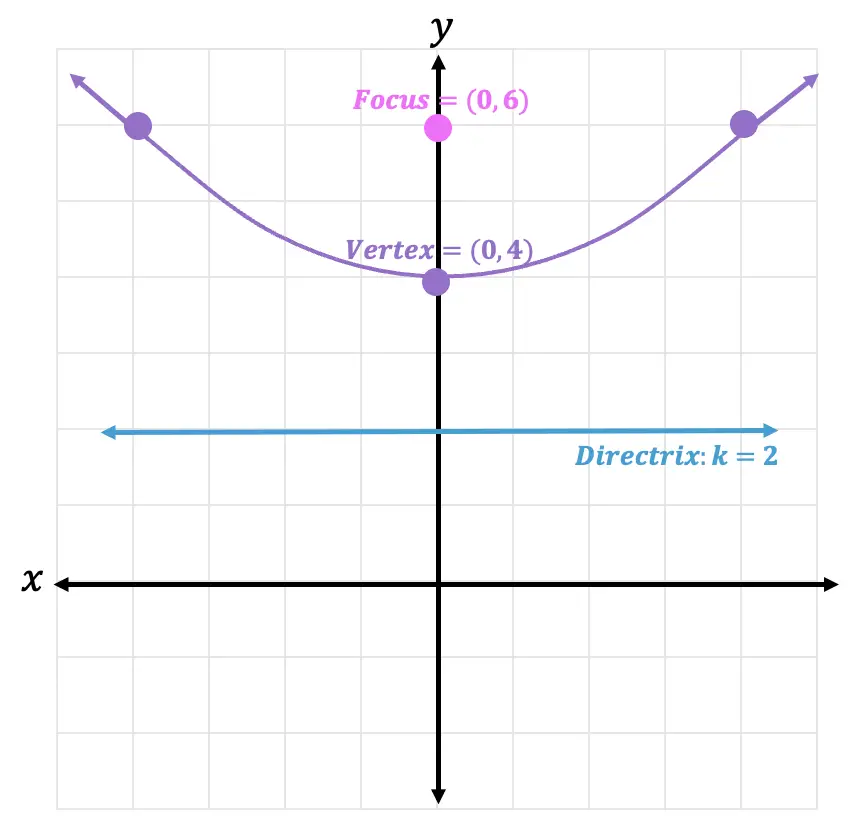
Parabola: A set of all points in a plane that are equidistant from a given point (the focus) and a given line (the directrix). The equation of a parabola in relation to the focus and the directrix is:
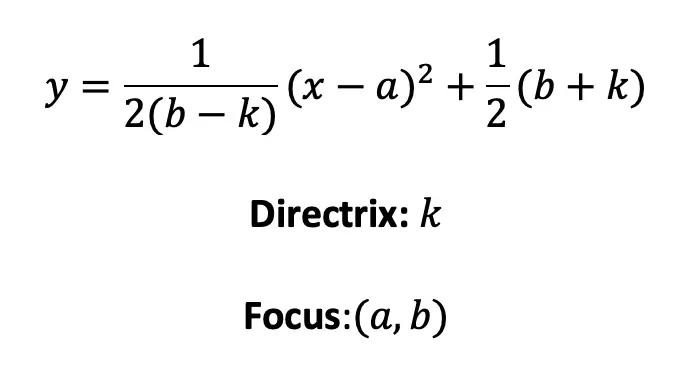
Vertex: The maximum or minimum point on a parabola. This coordinate point always lands on the parabola itself. Takes the coordinate form (a,(.5(b+k))) from the parabola equation above.
Focus: A coordinate point that is “inside” the parabola that has the same distance from the vertex as it does the distance between the vertex and directrix. Usually denotes as (a,b) within the parabola equation above.
Directrix: A horizontal line denoted as, “y= ” or “k= “, that is the same distance from the vertex when compared to the distance between the vertex and the focus.
The above definitions explain that every point on a parabola is equidistant from the vertex to the focus as it is to the directrix. In the picture below, we can see that the vertex is 2 units away from the focus and 2 units away from the directrix. They are equidistant:
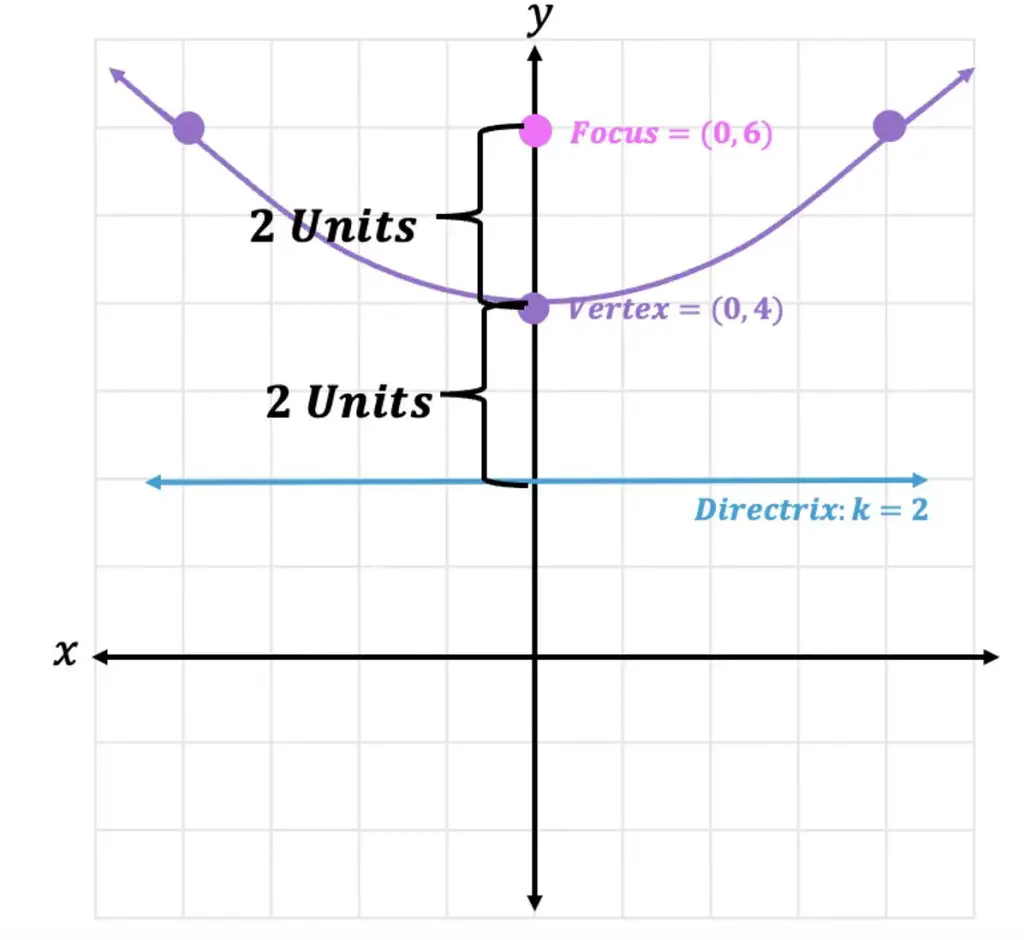
This phenomenon, works not just the vertex, but for each and every point found on a parabola!
We can see below the equidistance between several points on the parabola that compare the distance between the vertex to the directrix and the distance between the vertex to the focus. Notice that they are all the same!
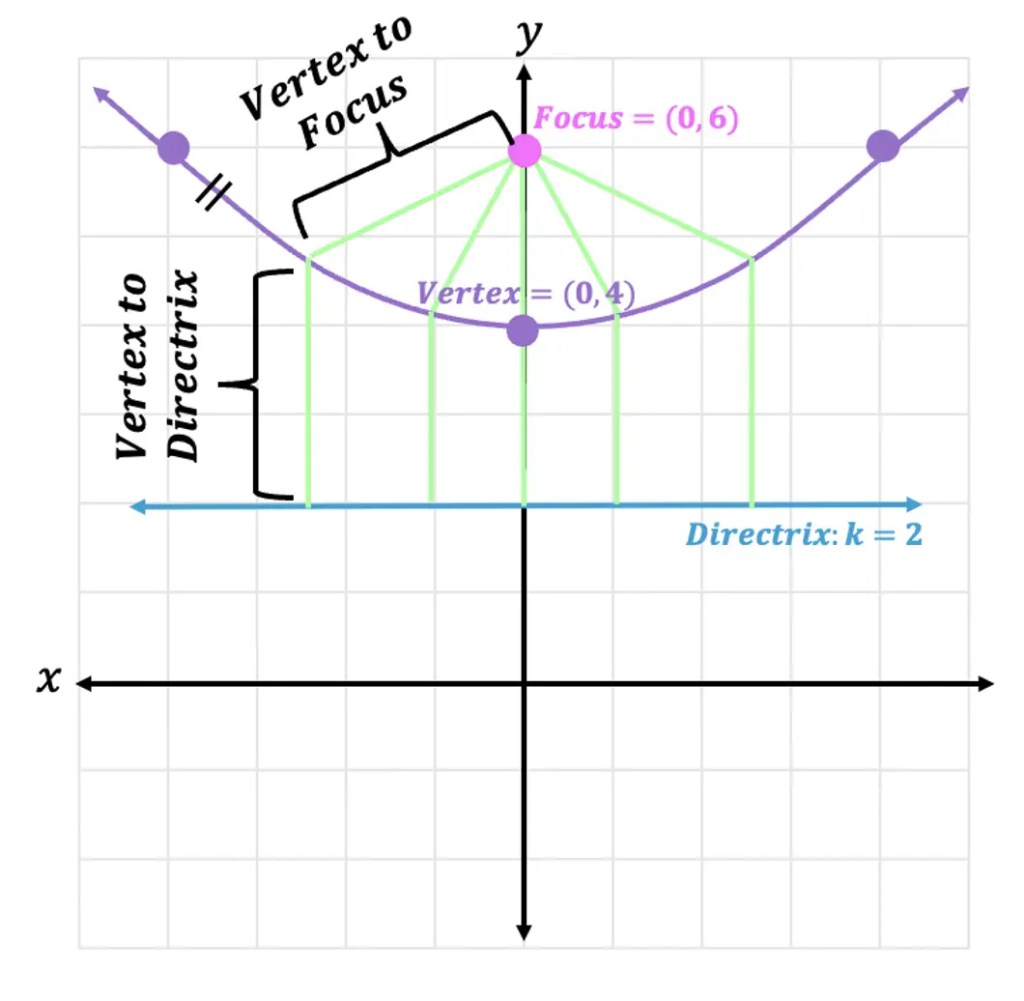
Ready to test our new knowledge with the following Example?

Step 1: First, let’s sketch out our parabola with the given information. We know that the vertex is at point (2,-1) a point that lies on the parabola itself, so let us map that out. We also know that the directrix is k=3 and is represented as a line as y=-3.
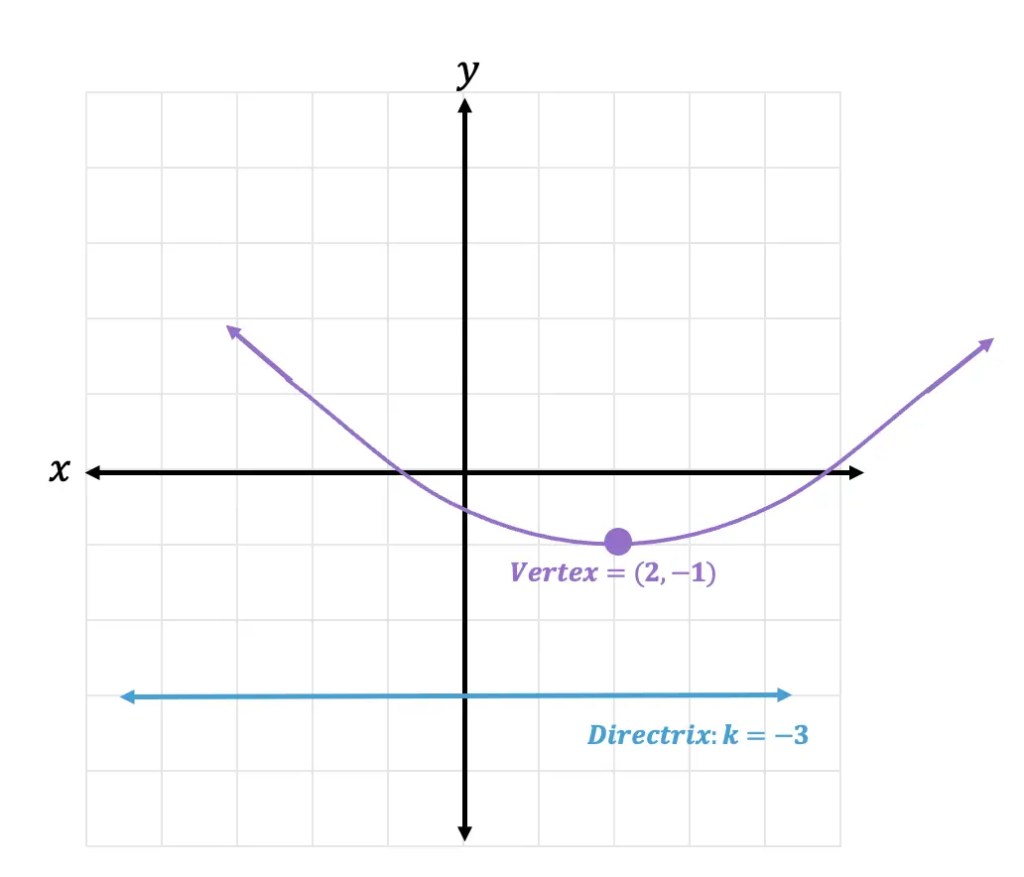
Step 2: Next, let us measure the distance between the directrix and the vertex. The distance between the vertex and directrix is 2 units. That means we must also measure the 2 units on the opposite side of the vertex to find the value of the focus. This leads us to the point (2,1).
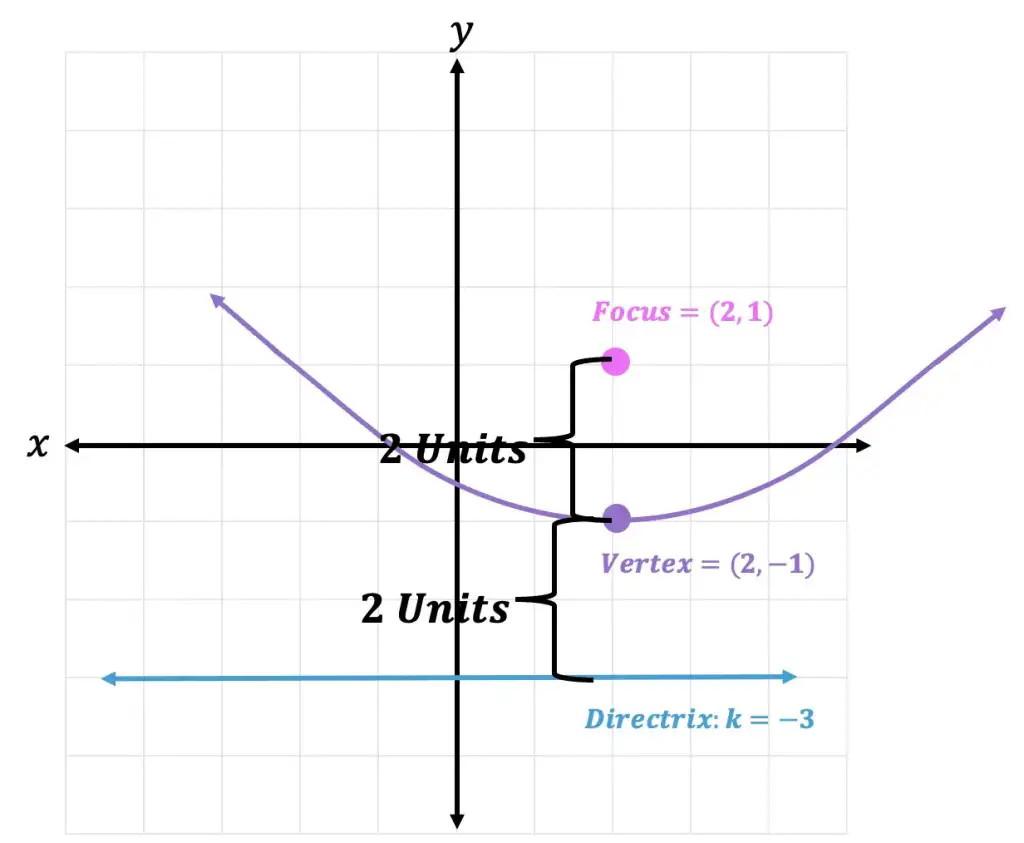

Now for part two of our question, how to find the equation of a parabola now that we have the value of the focus and the given directrix. For this, we will need to use the funky looking equation for a parabola mentioned earlier in this post.

Step 1: First we need to gather all of our information, the formula for the equation of a parabola , the given directrix, k=-3 and the focus we found in the previous example (2,1) which corresponds to the formula as a=2 and b=1.
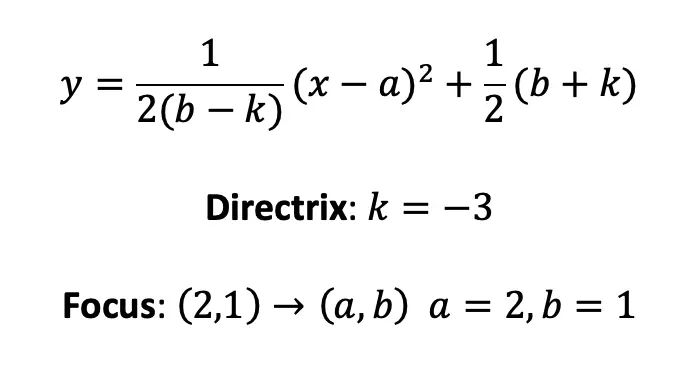
Step 2: Now, let’s plug everything into our formula where a=2, b=1, and k=-3, to find the equation to our parabola:
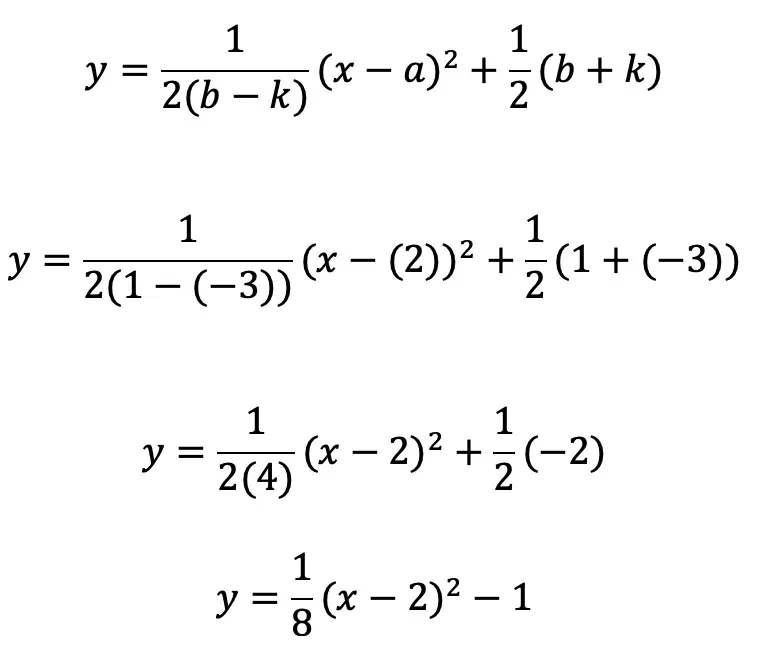
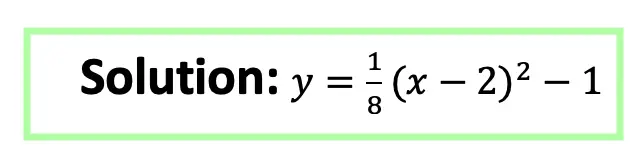

Practice Questions:

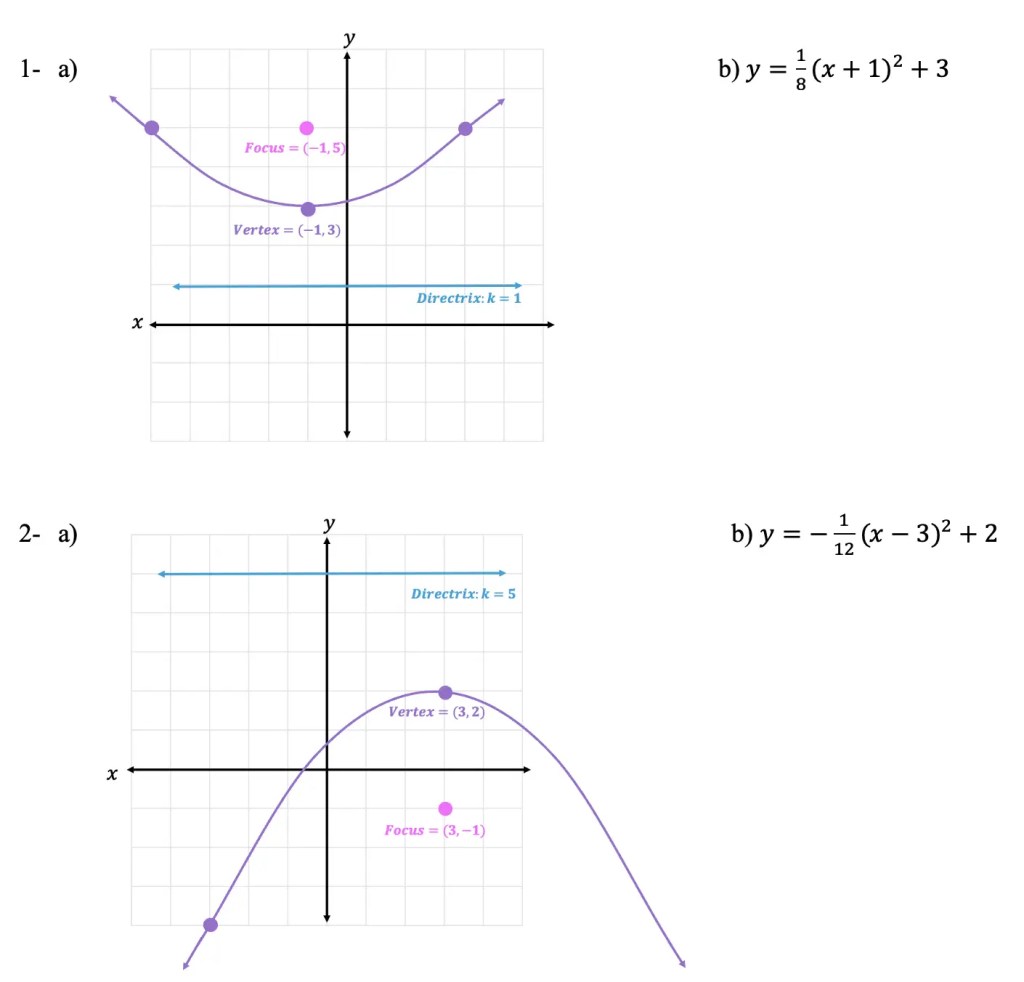
Solutions:
Still got questions? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Check out similar posts for Algebra 2/Trig. here!
Looking for more on Quadratic Equations and Functions? Check out the following Related posts!

I believe that 2b should is (-1/12)*(x-3)^2+2
Thanks for spotting my mistake. Updated the solution!