Howdy math friends! In this post, we are going to learn how to factor trig functions algebraically. This will combine our knowledge of algebra and trigonometry into one beautiful type of question! For more on trigonometric equations and the unit circle, check out this post here.
Solving trigonometric equations is very similar to solving the ho-hum everyday equations you solved all the way back in algebra 1, but this time we are solving for an angle value. If you need to refresh yourself on how to find x the old fashioned way via factoring be sure to check out this post here!
Solving trigonometric equations, sounds complicated? Well, you are correct, that does sound complicated. Is it complicated? Hopefully, you won’t find it that way after you’ve seen an example. We are going to find the value of x (value of the unknown angle) step by step in the following question:
Factoring Trig Functions Example: Linear Equation

How do I answer this question?
The questions want us to solve for x, the unknown value of the angle.
Step 1: Our first step for solving trigonometric equations is to pretend this is any other algebraic equation and we want to solve for x (Note: this is the key to solving any trig equation). Thinking this way, allows us to move radical 2 to the other side, by adding it to both sides of the equation.
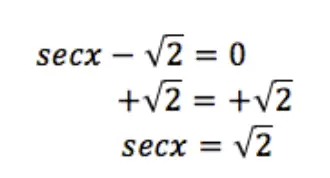
Step 2: Remember that secant is the inverse trigonometric function of cosine? Therefore we know that, secx is equal to 1/cosx and we can re-write the equation below, making the trigonometric function look a lot less complicated already!
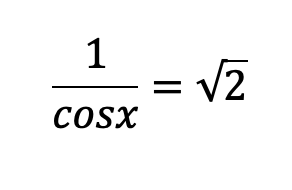
Step 3: Now we need a value for x. This is where I turn to my handy dandy special triangles. There are two main special triangles in trignometry we can use to solve our equation, the 45 45 90 triangle and the 30 60 90 triangle. In this case, we are going to use the 45 45 90 special triangle, because its proportions include a value of radical 2, which is exactly what our equation has!
*Note- In this case we can use our special triangles, but in other examples, we may also need to use our knowledge of trig identities to re-write the original trigonometric function.
Below we can see the proportions that the 45 45 90 special triangle brings us. When we apply the basic rules of trigonometry and SOH CAH TOA, we see that we can find the value of our missing angle x, which is 45º.

*Another way we could have gotten 45º without using special triangles is by plugging in cos-1 (1/rad2) into our calculator, this would also give us the solution of 45º!
Step 4: We have a value for cos45º=1/rad 2, but remember we need its inverse and must flip the fraction, to find the value of our angle of the inverse of cosine, secx, which flipped, is going to be 45º.
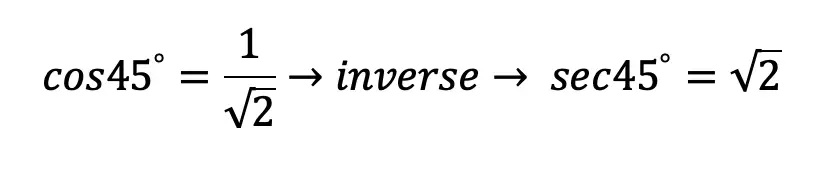
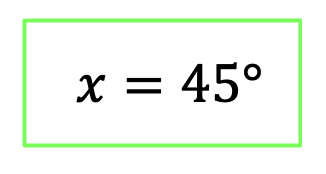
***But wait! We are not done yet! We have found only one part to our solution, x=45º, which is great! But we need to ask ourselves, are there any other angle measures that could potentially give is the right solution as well!? And thats where we need to consult the unit circle!
Step 5: Using the unit circle below, we can identify what other values can work for our original trigonometric function. Based on the unit circle below, we can identify which trig functions (sin, cos, tan) are positive in which quadrants, positive and negative angles (positive counterclockwise, negative clockwise).
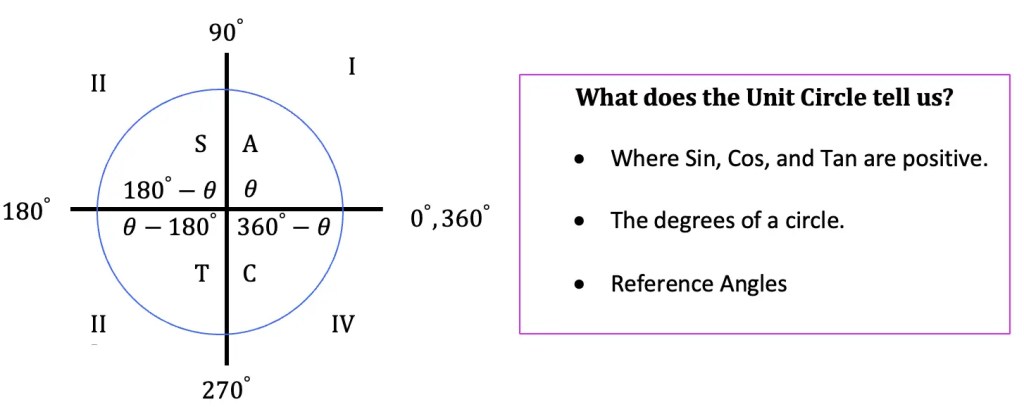
Notice that cosine is positive in Quadrants I and IV. That means there are two values that x can be (one in each quadrant). We already have x=45º from Quadrant i. In order to get the other value in Quadrant IV, we must subtract 360º-45º=315º using our reference angle (360º-θ) and giving us our other value for x, 315º, completing our answer!

The above example is similar to a linear equation, let’s look at another type of trigonometric equation that is more similar to quadratic equations.
Factoring Trig Functions Example: Quadratic Equation

Step 1: First let’s move everything onto one side of the equation. We can start by multiplying tanθ to both sides and distributing, multiplying (2tanθ-7)(tanθ). Then we can subtract the 4 from both sides. Remember to solve trigonometric equations, we always want to treat them like a normal algebraic function.
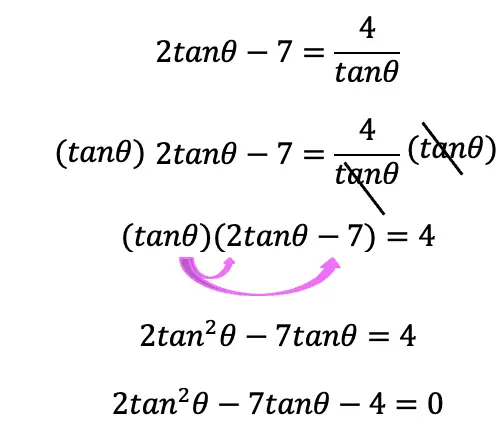
Step 2: Now that we have something resembling a quadratic equation, we have something to work with! There are two main ways to solve for our unknown angle via factoring for this example, (1) The Quadratic Formula, or, (2) Factor by Grouping. In this case, we are going to be using factor by grouping to find the value of our angle, and the solution to our problem, but the quadratic formula should work as well!
Factor by Grouping: First find the product, sum and factors of the equation.
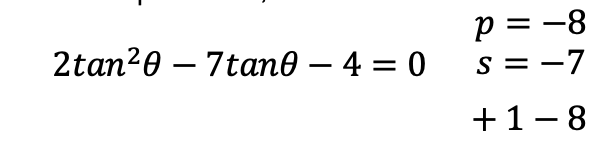
Now that we have our factors, we can re-write our equation, converting -7tanθ into -8tanθ + tanθ.
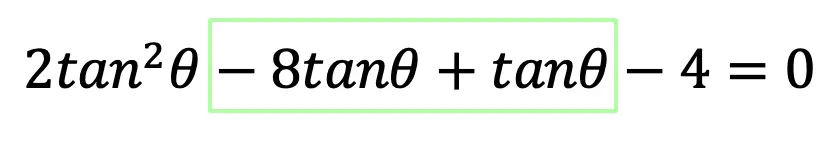
Next, we split the equation down the middle and take the GCF of each side.
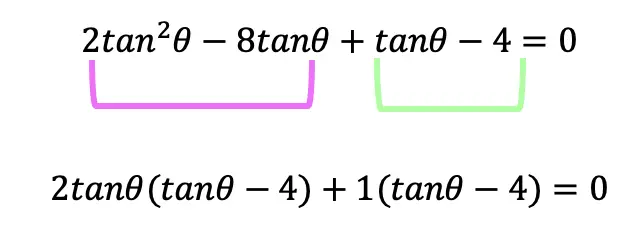
Finally, we can combine the values outside our parenthesis 2tanθ+1 and the matching values found within our parenthesis and tanθ-4.
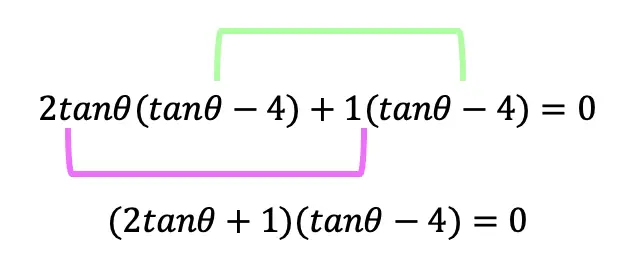
Step 3: Now we can use our equation and solve for each angle value, by setting up each group found in the parenthesis equal to zero, just like we would when finding the value of x in a normal algebraic equation.
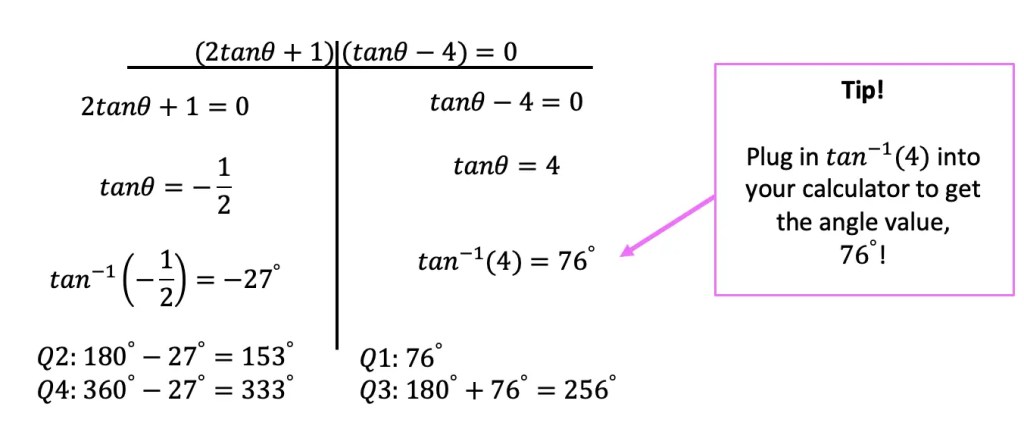
Based on finding our two angles for θ, -27º and 76º, we are able to find the angles that apply to our specific trigonometric equation listed below, based on where tanθ is positive and negative in each quadrant of the unit circle. In this case, the angle value of -27º, we look for the angle values where tangent is negative which are in quadrant ii and quadrant IV, and apply our reference angles. On the other hand, the angle value of 76º, is positive, therefore, we look for angles where tangent is positive, in quadrant i and quadrant iii, and apply our reference angles to get the correct value of each angle.

*Note! In the above two examples, we look at a cosine function and a tangent function, but the same exact methods apply to a sine function!
Think you are ready to solve trigonometric equations on your own? Check out the practice questions and solution to each below!
Practice Questions:
Find the nearest degree to all values of θ or x in the interval 0º < θ < 360º and 0º < x < 360º:

When you are ready check each solution below!
Solution:

Does the solution to each trig function make sense? Great! 🙂 Do you think it is clear as mud to solve trigonometric equations? Alas, I have failed. But I have not given up (and neither should you). Ask more questions, look for the spots where you got lost, do more research and never give up! 🙂
Hopefully, you enjoyed my short motivational speech. For more encouraging words and math, check out MathSux on the following websites! Sign up for FREE math videos, lessons, practice questions, and more. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Related Trigonometry Posts:
Basic Right Triangle Trigonometric Ratios (SOH CAH TOA)
Graphing Trigonometric Functions

3 thoughts on “How to Factor Trig Functions”