Greetings math peeps! In today’s post, we are going to look at how to solve for exponents. At this point, we are familiar with solving for unknown variables within an equation, but never before did we have to solve for an exponent! Understanding how to do this and what method(s) to use will take our algebra skills to a whole new level. Also, don’t forget to check out the video and practice questions in this post for even more examples. Happy calculating! 🙂
What is an Exponential Equation?
An exponential equation, is an equation where the exponent is an unknown variable and takes the following form:
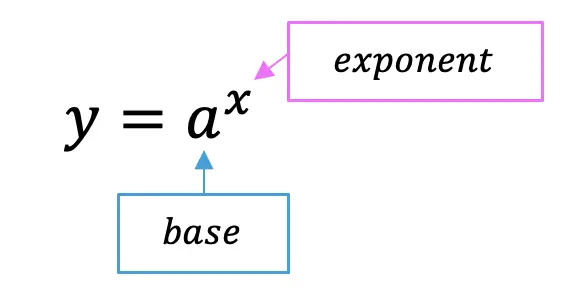
Sometimes we will be asked to solve for the unknown variable in an exponential equation. There are two main ways of solving for this type of equation and we’ll go over each type below.
(Method 1) Same Base
(Method 2) Different Base
Let’s dive right in and look at three different examples applying one of the two methods above.
Example #1: Solving Exponential Equations with the Same Base
Whenever an equation has the same base, like in the example below (both bases are 5), we can set the exponents equal and solve for the missing variable.
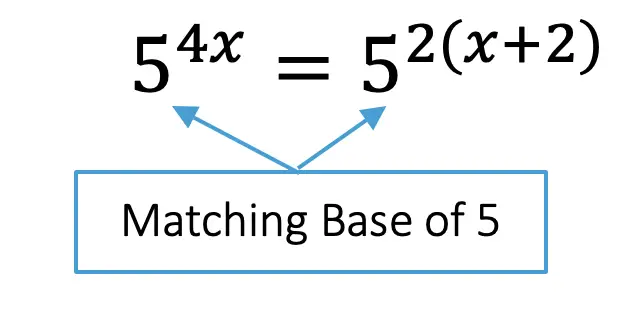
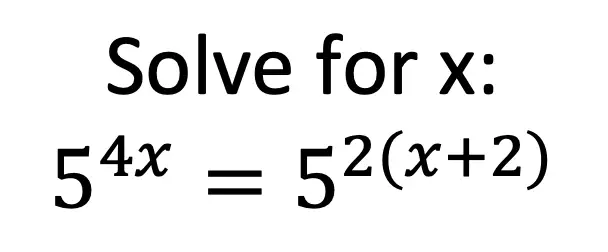
Step 1: Since both sides of the equation have the same base (a base of 5), we can set the exponent values equal to each other and use basic algebra to solve for x.
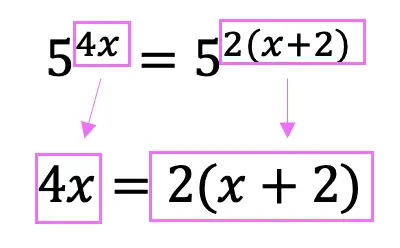
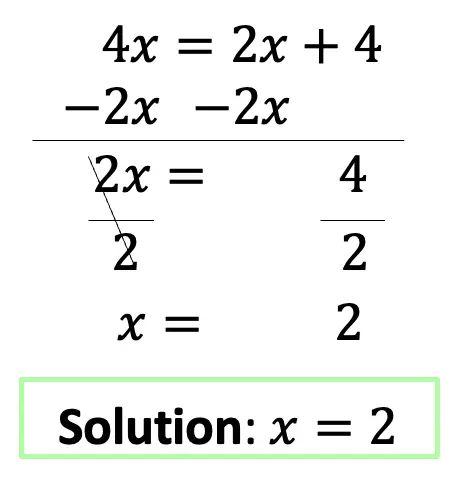
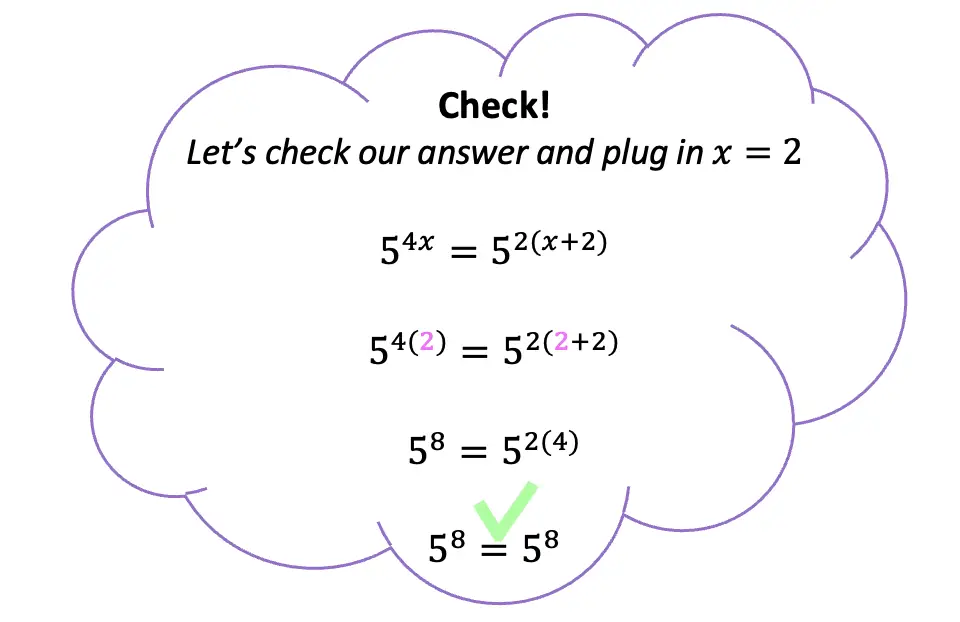
Example #2: Solving Exponential Equations with the Same Base
We can set exponents equal to each other whenever an equation can be written to have the same base on either side. Like in the example below both bases can be written as 5, we can again, set the exponents equal and solve for the missing variable.
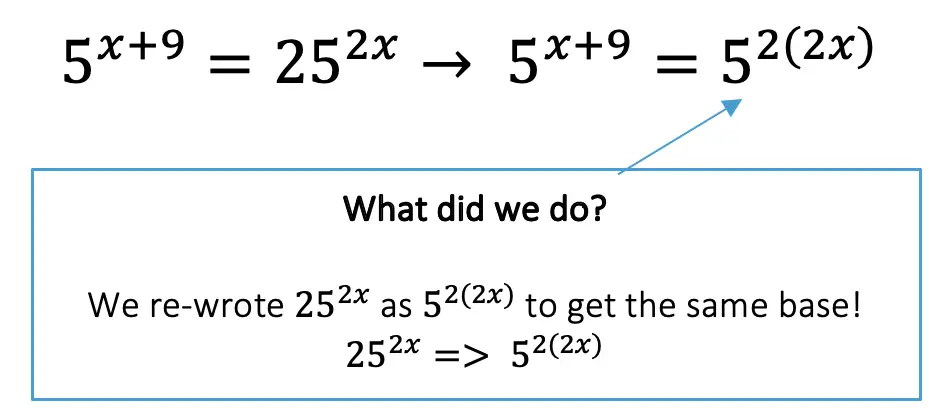
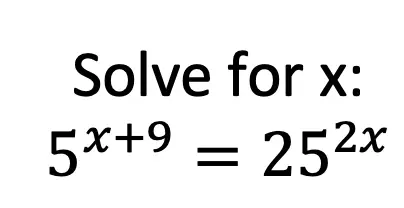
Step 1: Re-write the right part of the equation so the bases on either side match. In this case we need to re-write 25 as 5^2. Make sure to keep the part of the exponent, 2x, that was already attached to the 25 so it becomes, 5^2(2x).
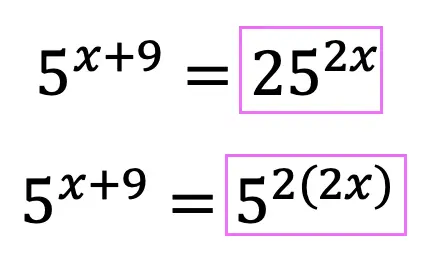
Step 2: Now we can set the exponent values equal to each other and solve for x now that both sides have matching bases.
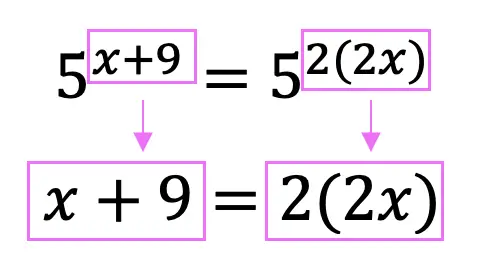
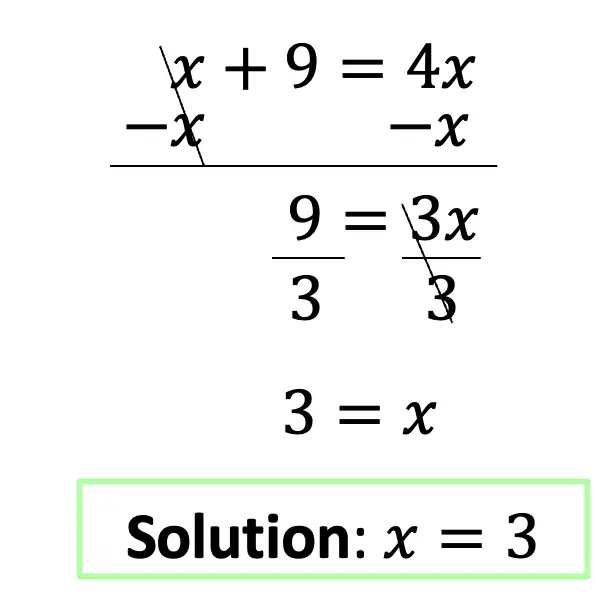
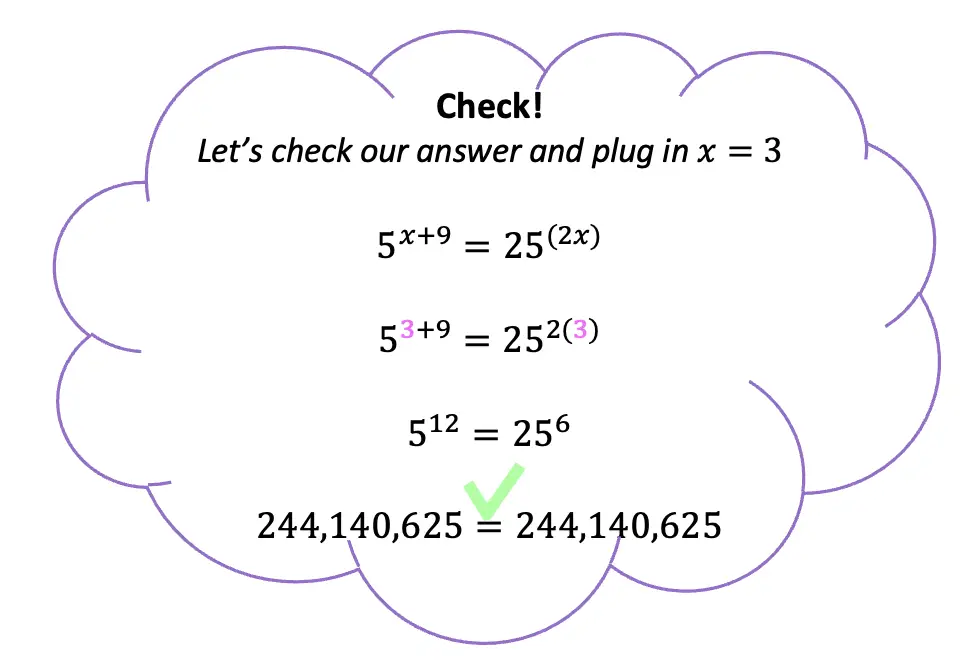
Example #3: Solving Exponential Equations with the Different Bases
When an exponential equation doesn’t have the same base and cannot be written to have the same base, we must use logs to solve for the unknown variable! So, make sure you are comfortable with the log rules listed here in order to solve these types of questions. We are mainly going to be working with the power rule of logs.
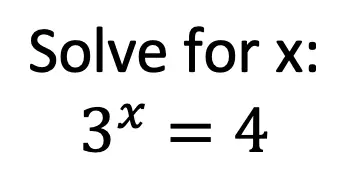
Step 1: Take log of both sides and solve for x.
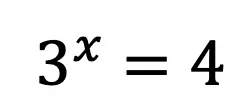

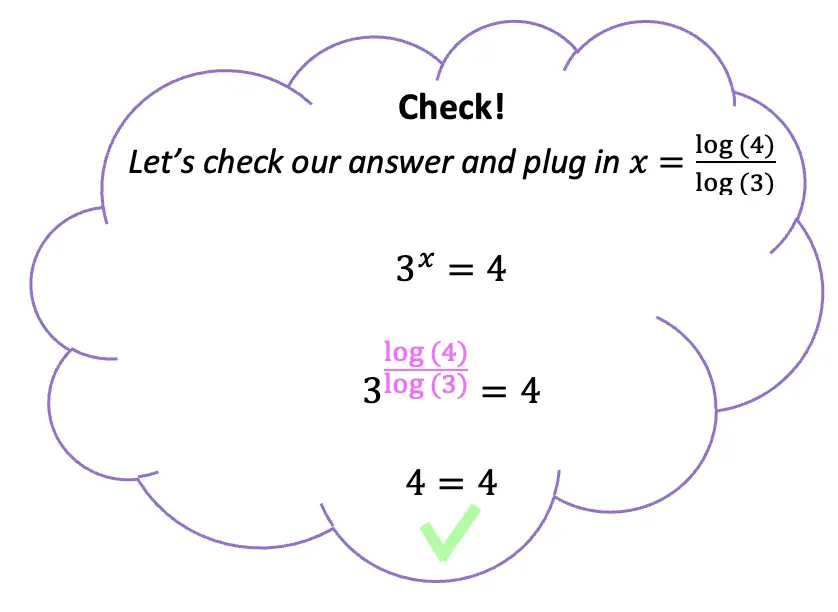
When you’re ready check out the practice questions below to own your new exponent skills!
Practice Questions:
Solve each exponential equation for x.

Solutions:

Looking to review logs? Check out this post here!

2 thoughts on “How to Solve for Exponents”