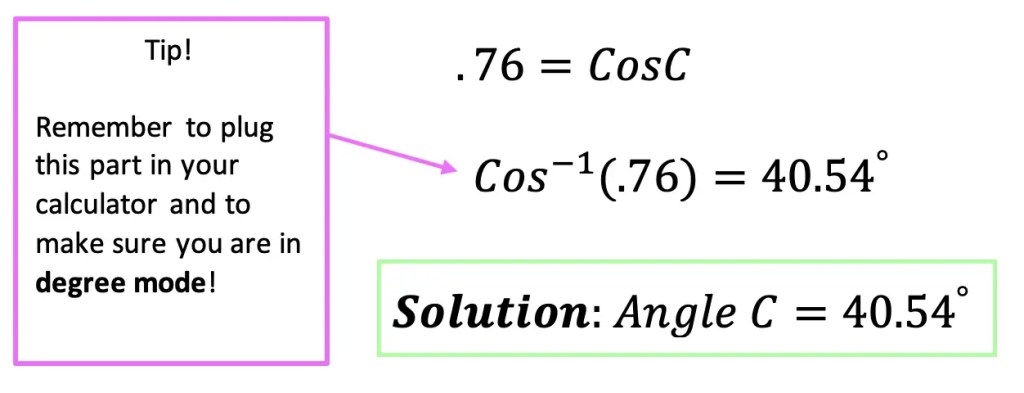
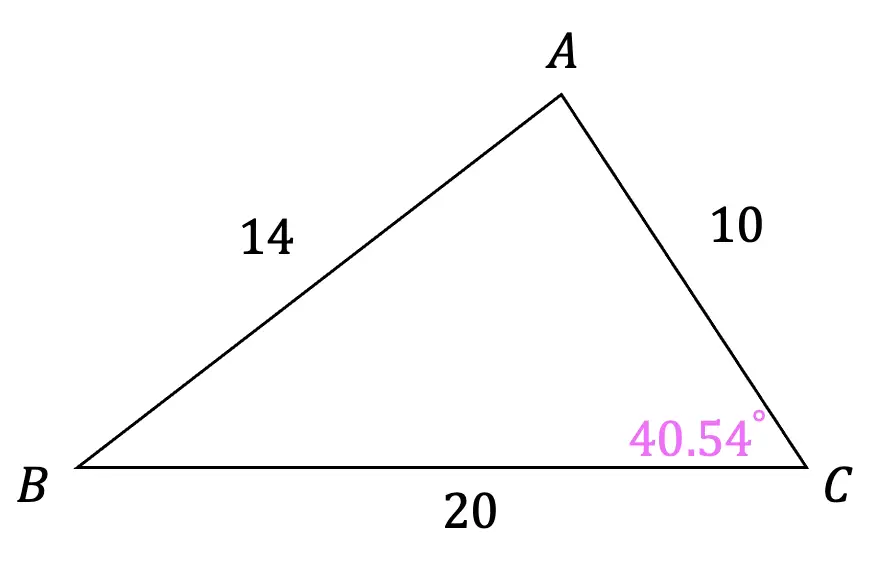
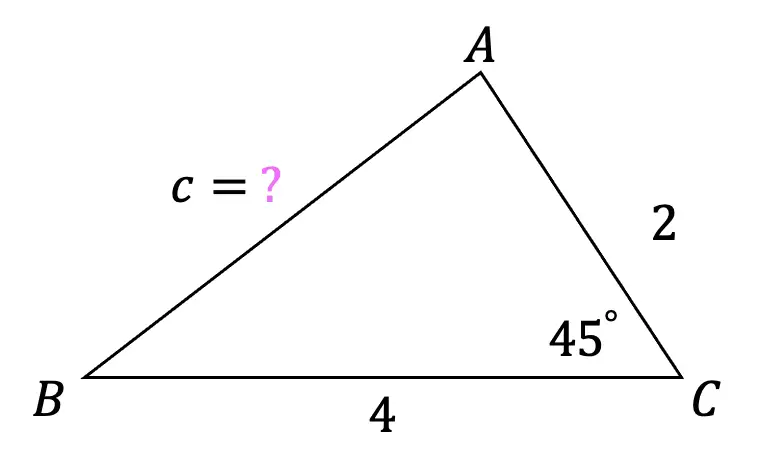
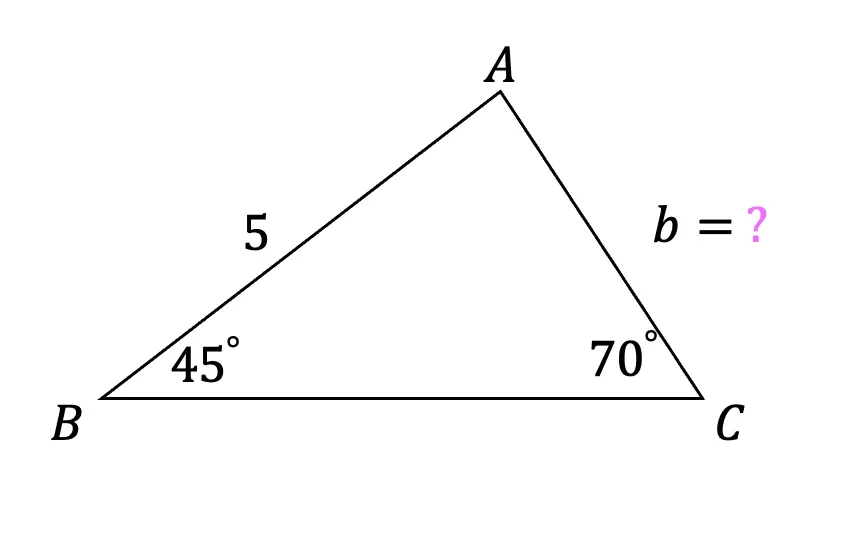
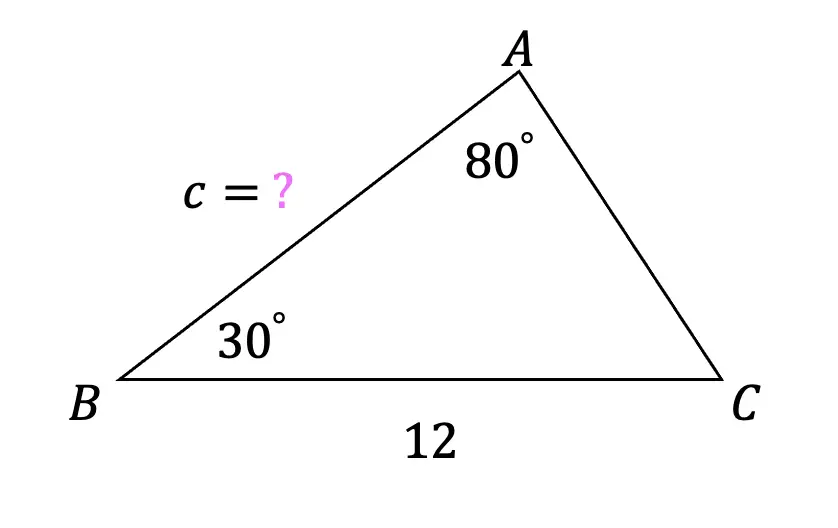
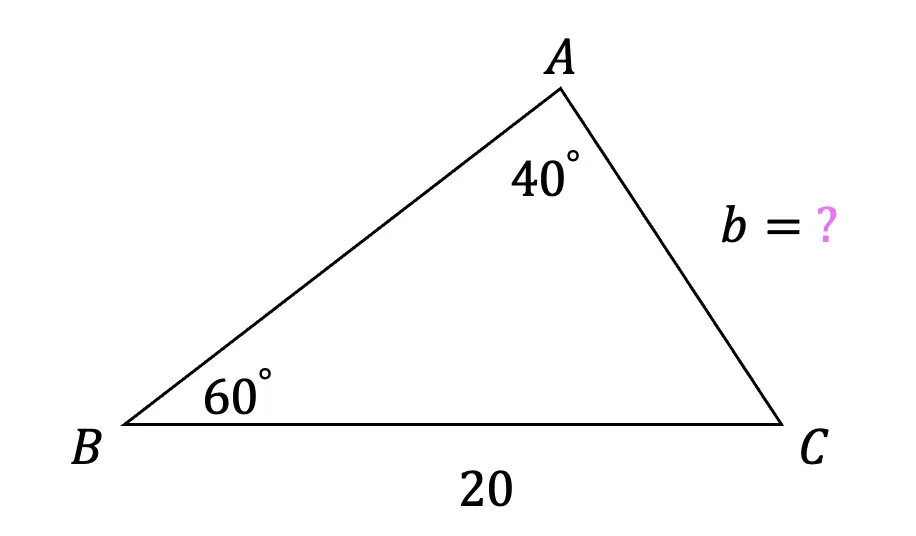
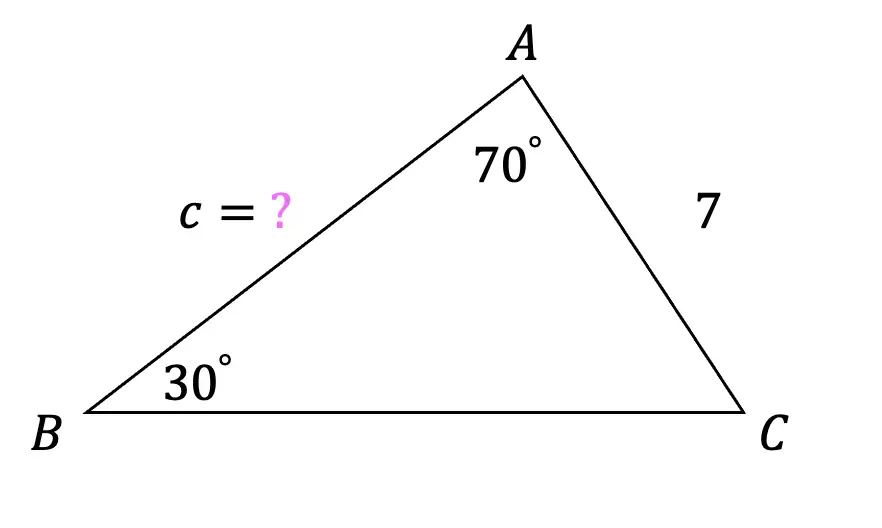
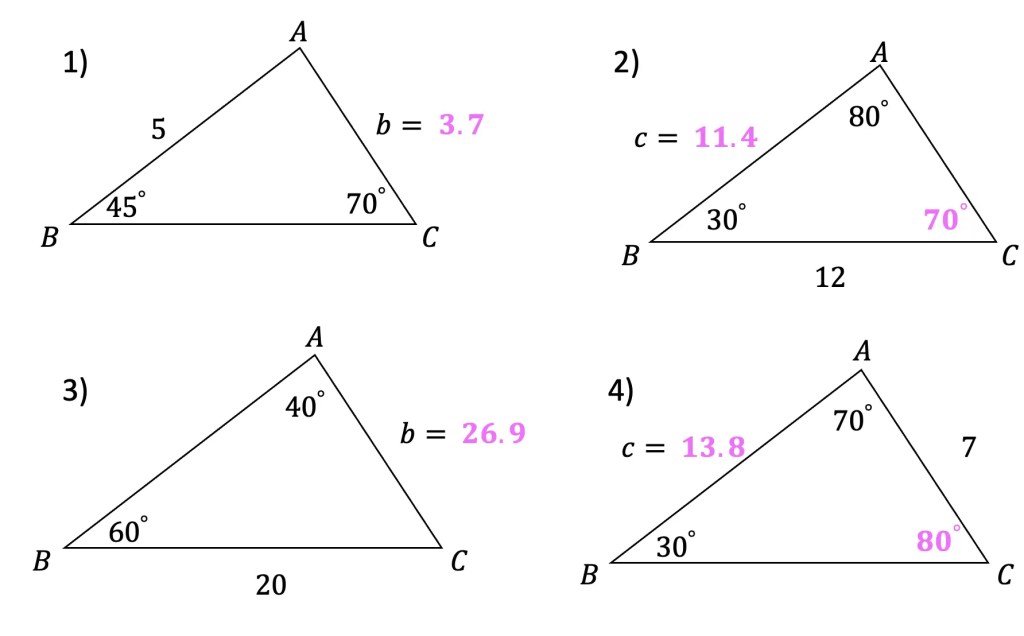
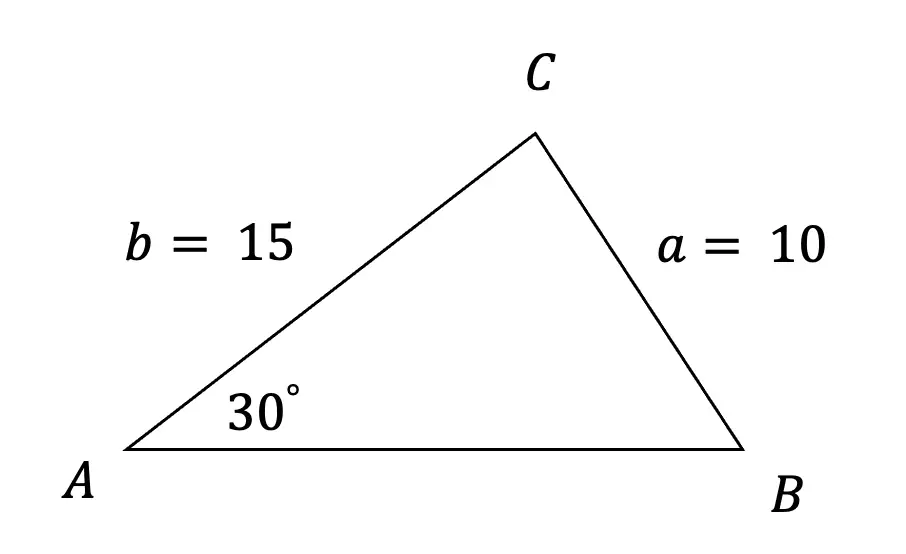
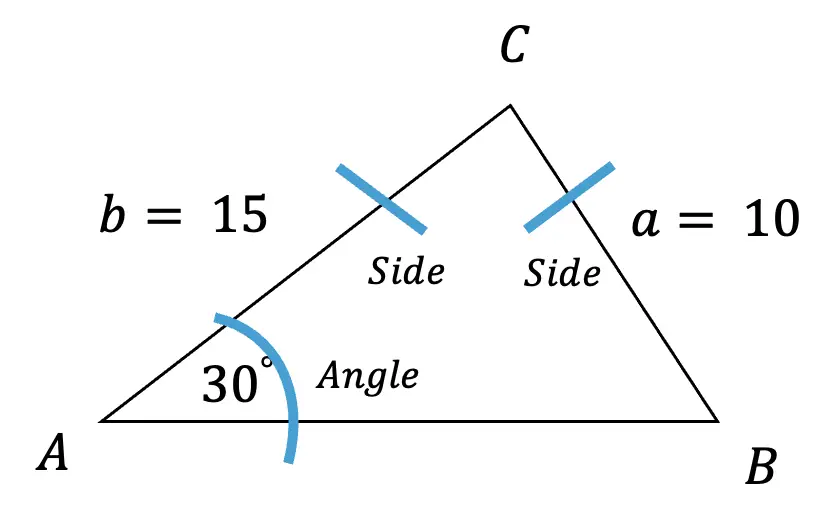
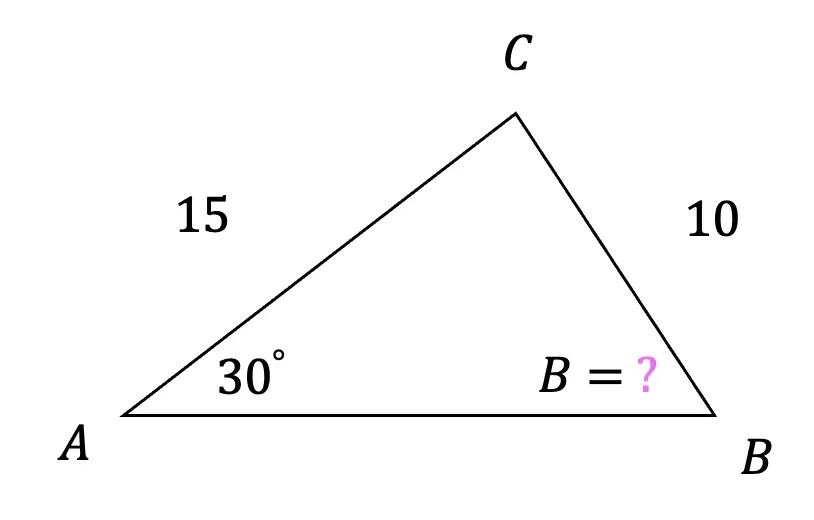
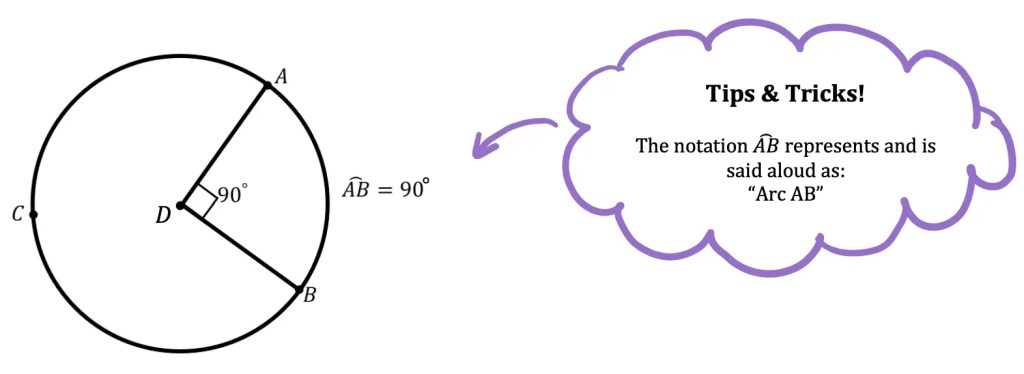
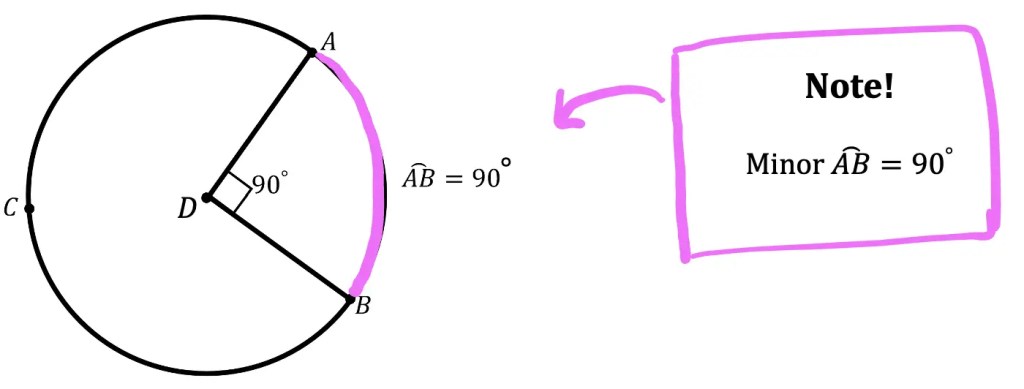
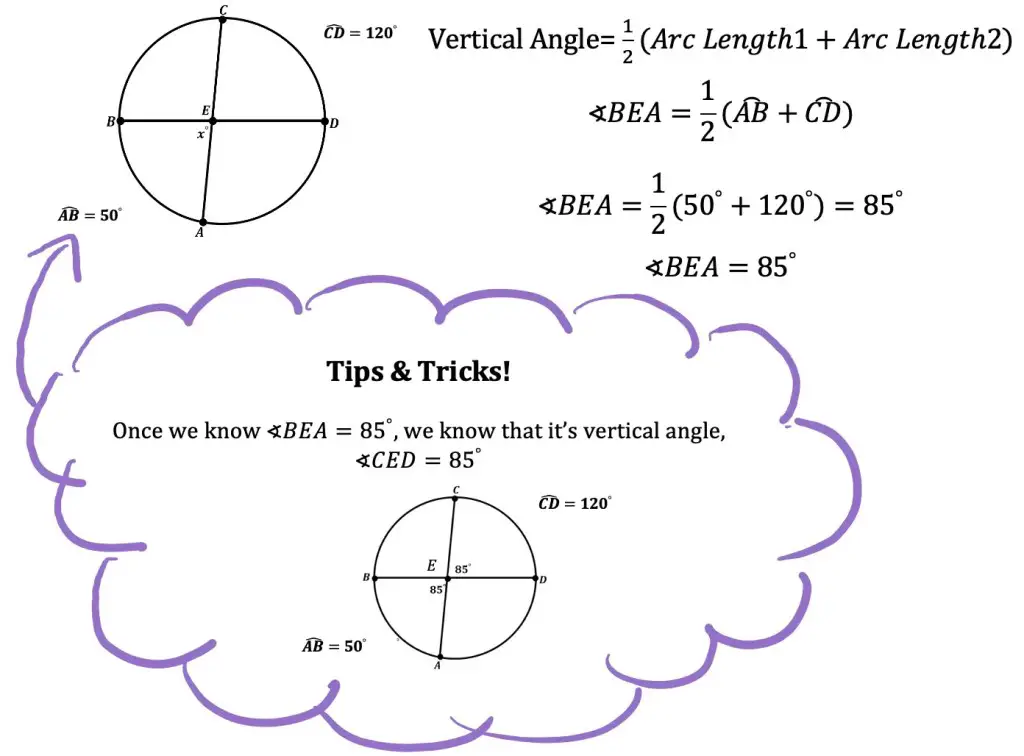
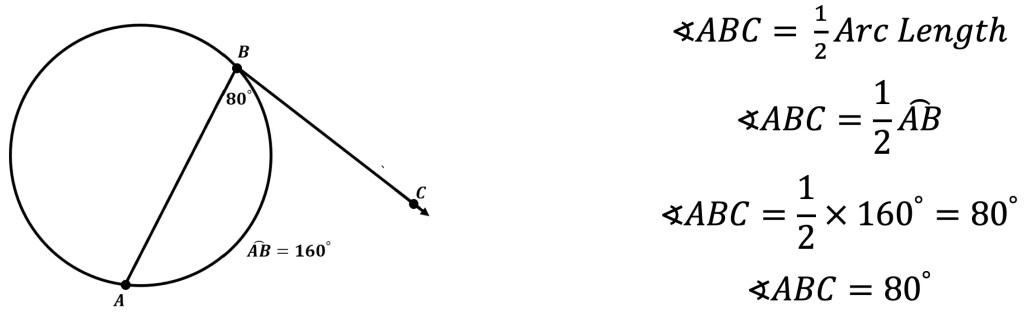
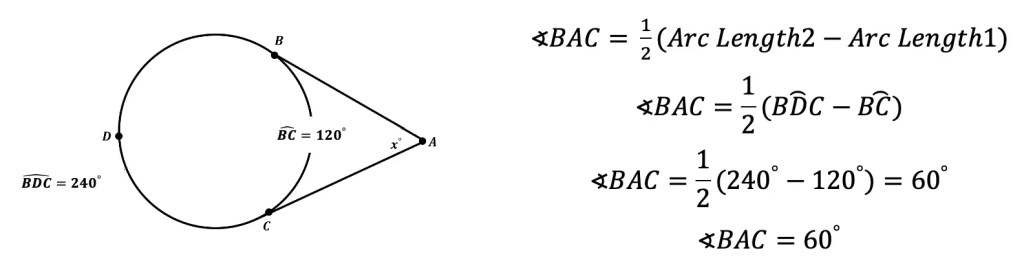
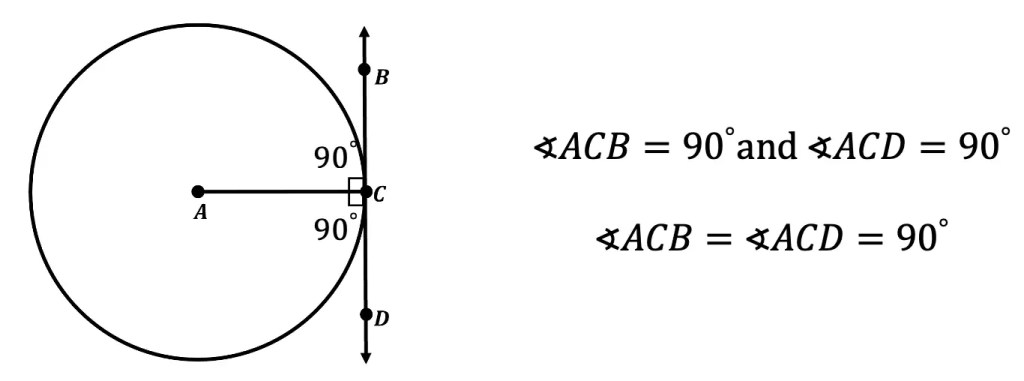
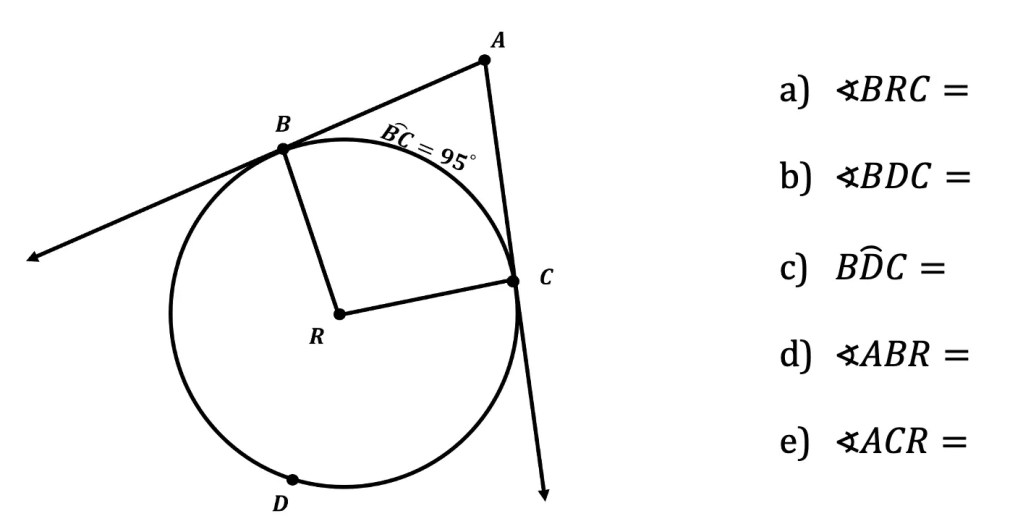
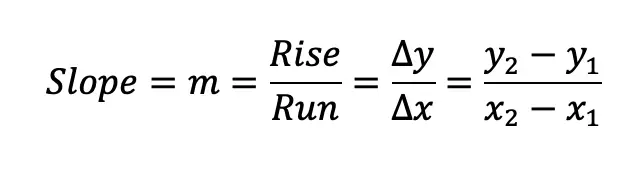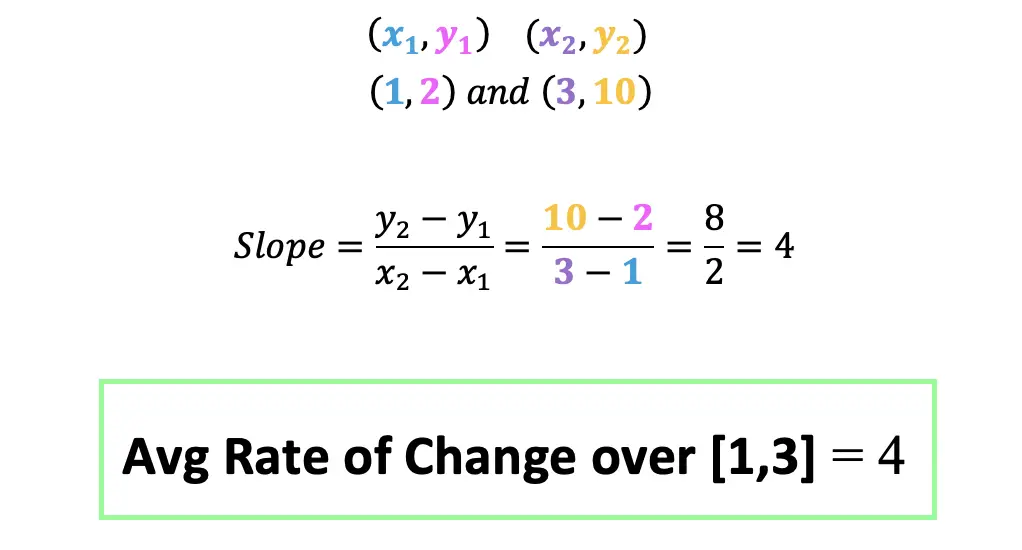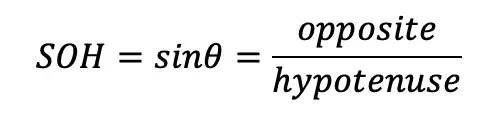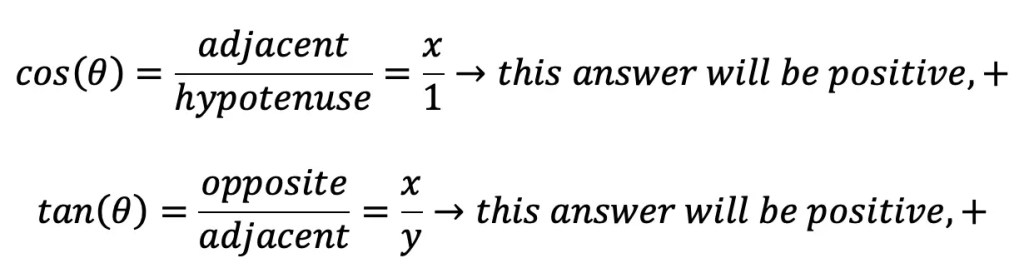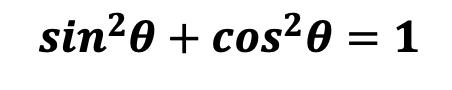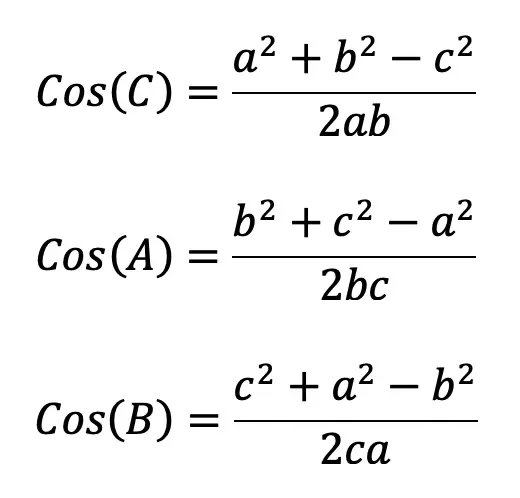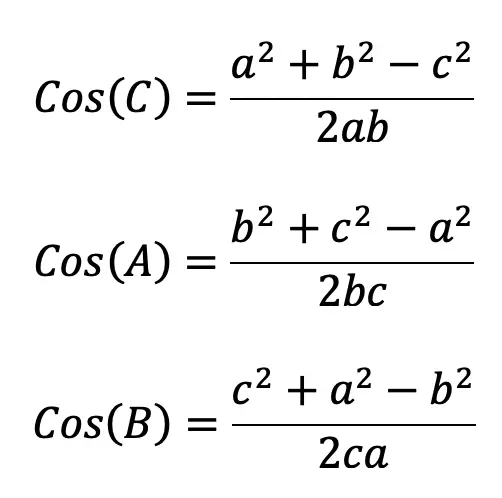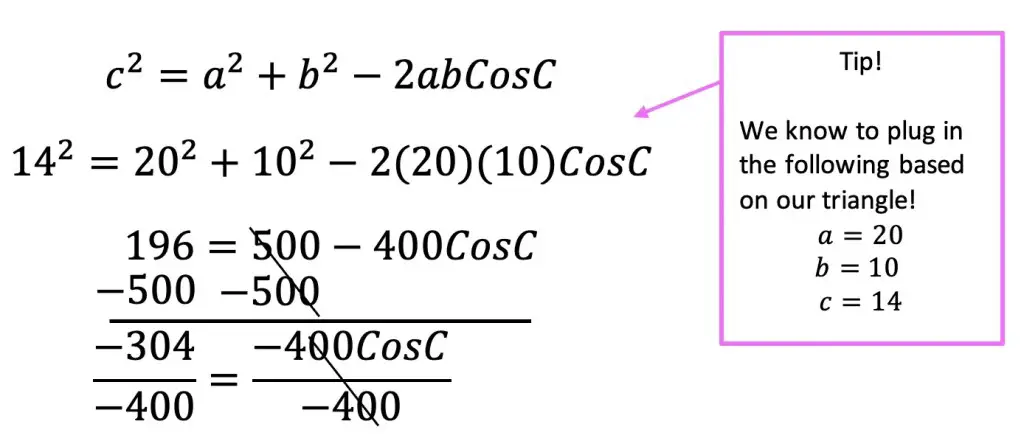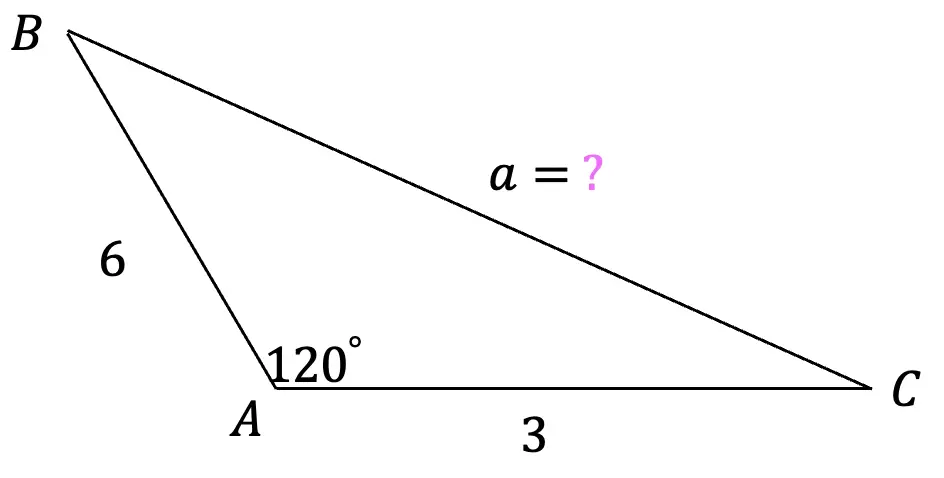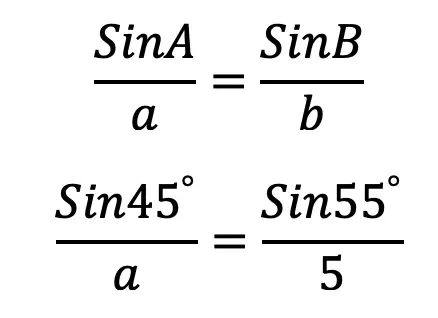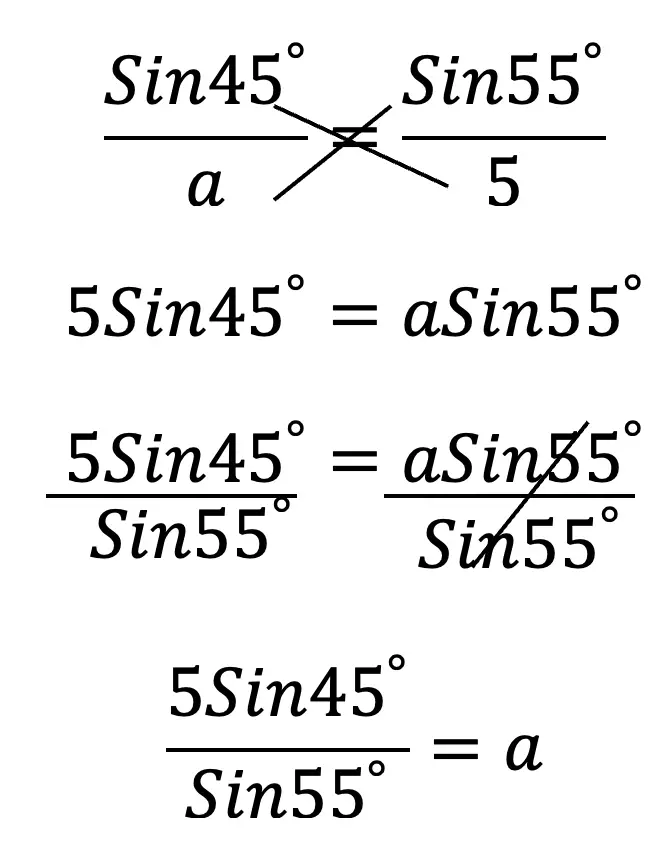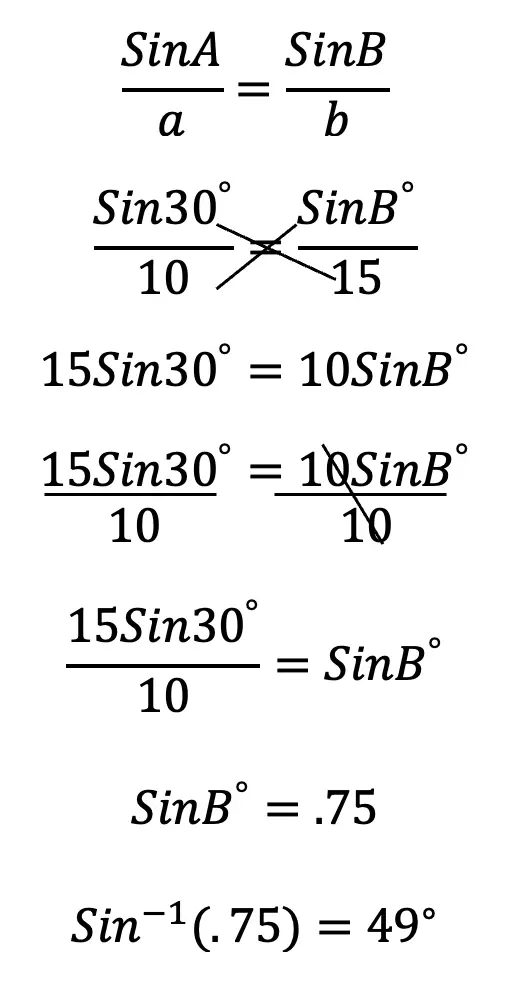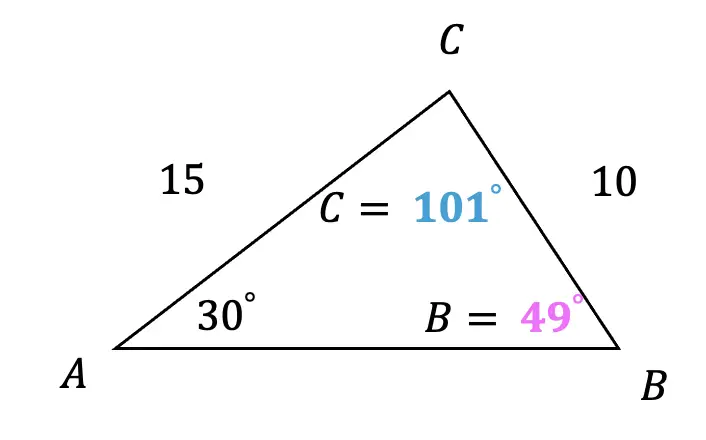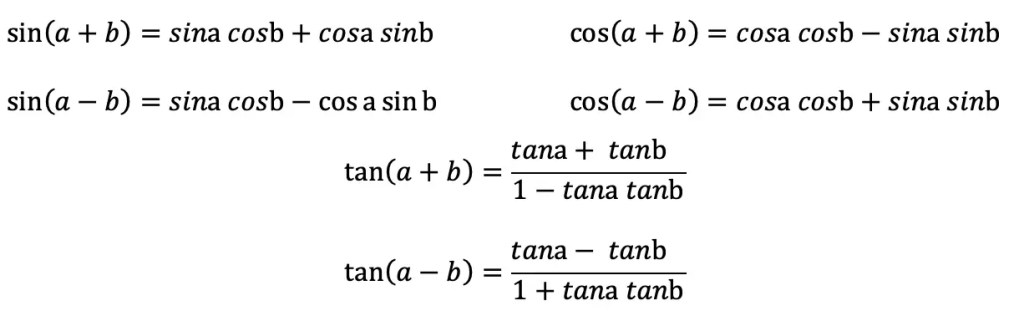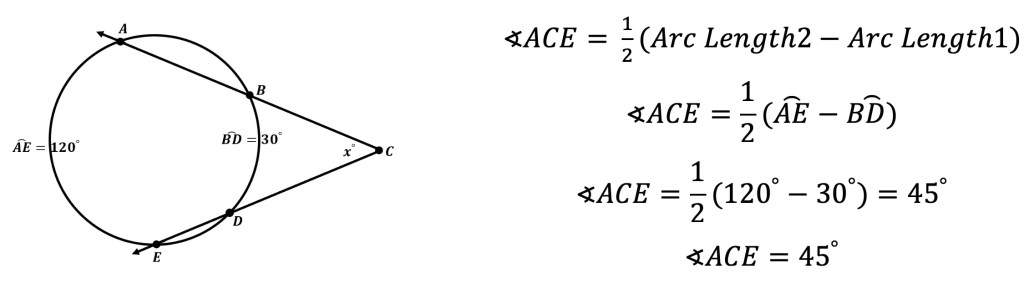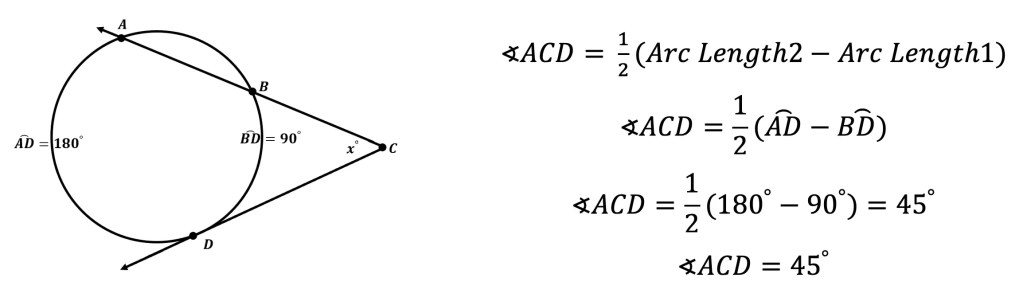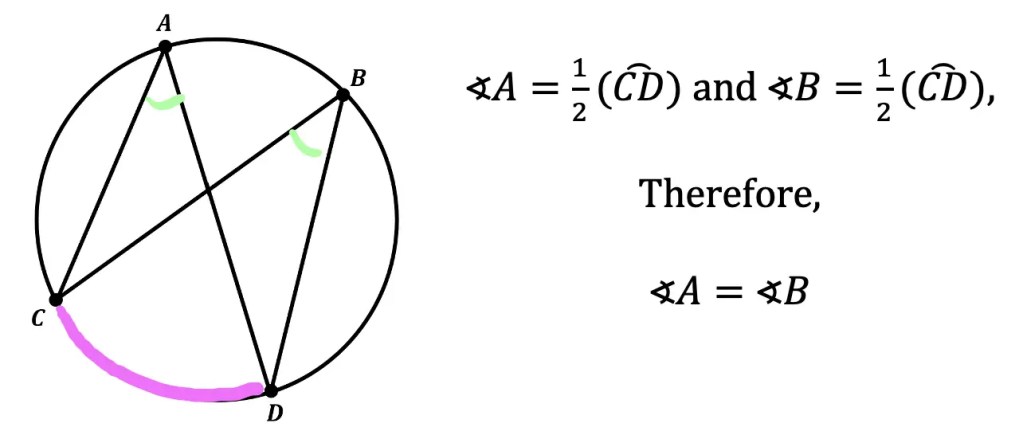What is a sequence? A sequence is a specific list of numbers where each subsequent term is based on the previous term forming a pattern. Sequences can be infinite and go on forever, or they can be finite and end after only 5 terms. In this post, we are going to dive into one the most famous sequences of all time, drum roll please… the Fibonacci Sequence!
Why is the Fibonacci sequence so special? The Fibonacci sequence is a unique type of sequence because it is not only found in numbers, but found in nature, art, and life itself! Keep reading to learn more below!
History of the Fibonacci Sequence
The Fibonacci sequence is a profound one at that discovered by the Italian mathematician Leonardo Fibonacci, otherwise known as “Leonardo of Pisa” during the 13th century.
Leonardo studied Indian mathematicians sources and wrote his findings in a book titled the Book of Calculation or “liber abaci.” This was the first time the mathematical ideas from India were translated for a western audience in the 1200s. To find out more on the history of the Fibonacci sequence and the liber abaci, check out this resources at the end of this article.
Where did the Fibonacci sequence come from? The sequence is actually based on a problem involving a rabbits population. Read more about the details of this mathematical quandary by following the link in the resources section at the end of this article.
Fibonacci Sequence – The Most Famous Sequence!
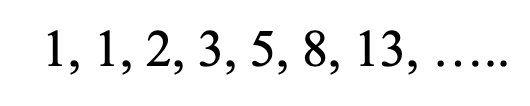
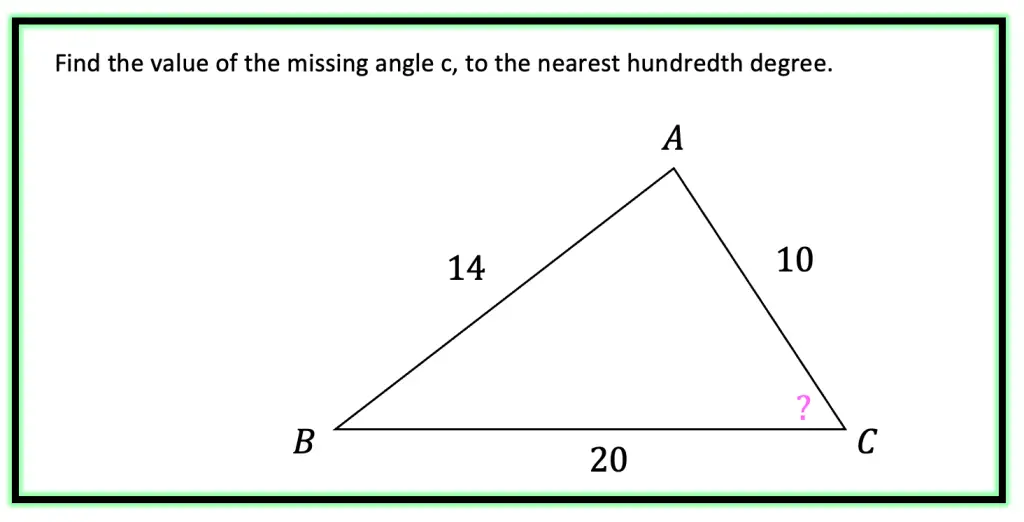
The above sequence, known as the “Fibonacci sequence,” is one of the most famous sequences in the world! How can a sequence be so famous? Why is it so special? Well, we’ll get to that in a minute, but before we do, can you see how the Fibonacci sequence forms a pattern? What would be the next term? Take a guess!
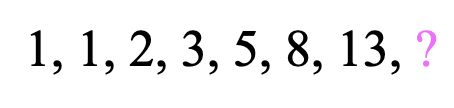
Take your time, trying to figure out the next term of the sequence before checking the answer below:
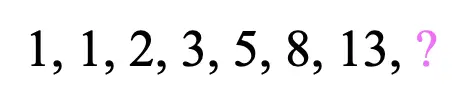
Why!? Fibonacci Numbers Explained
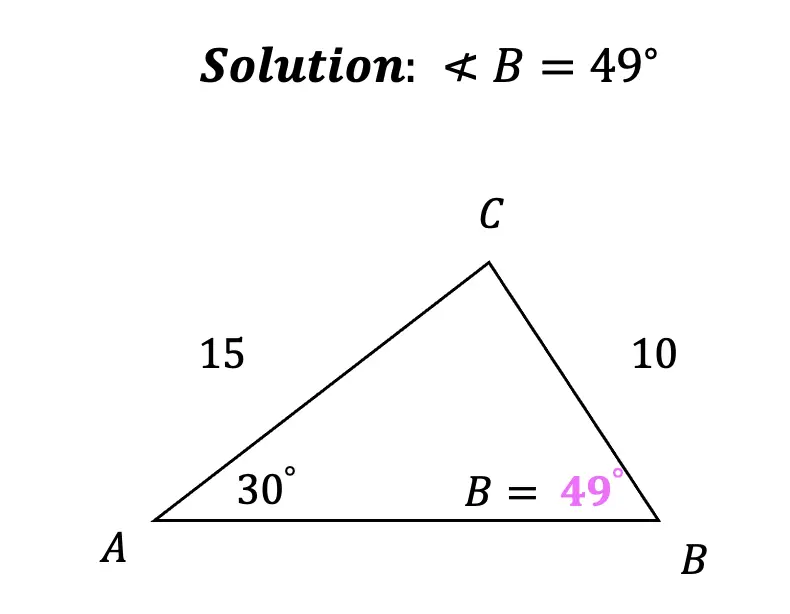
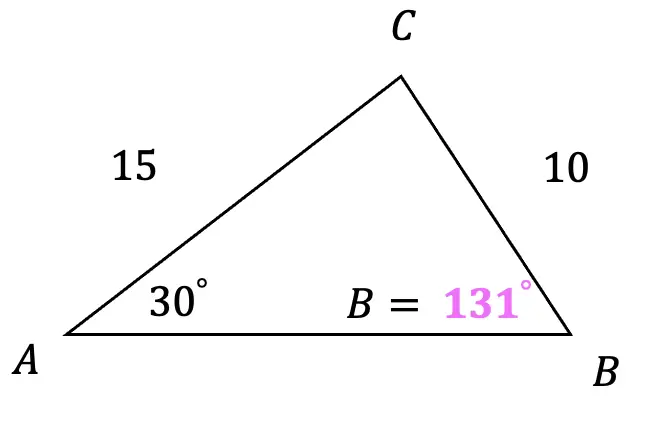
The next term of the Fibonacci sequence is 21! The pattern of this sequence is all about adding the two previous terms together. That’s how we get 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, which brings us to get our missing term, 8+13=21. Take a look at how this sequence works below:

Why is the Fibonacci Sequence Famous?
Now that we know the secret pattern behind this sequence, let’s look at why the Fibonacci sequence is so special! The Fibonacci sequence’s main claim to fame is that it is found throughout art, architecture and even in nature via the golden ratio.
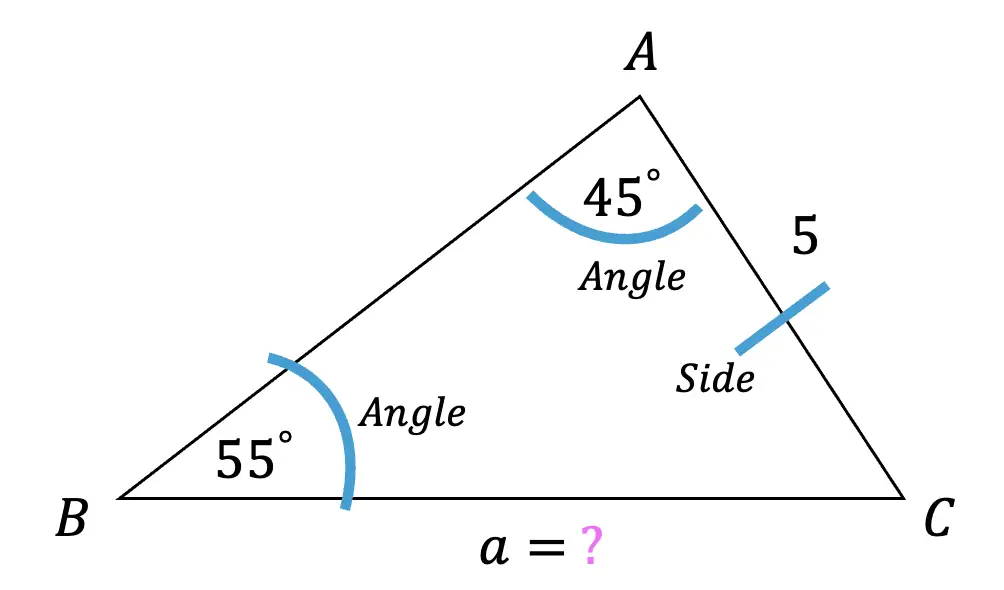
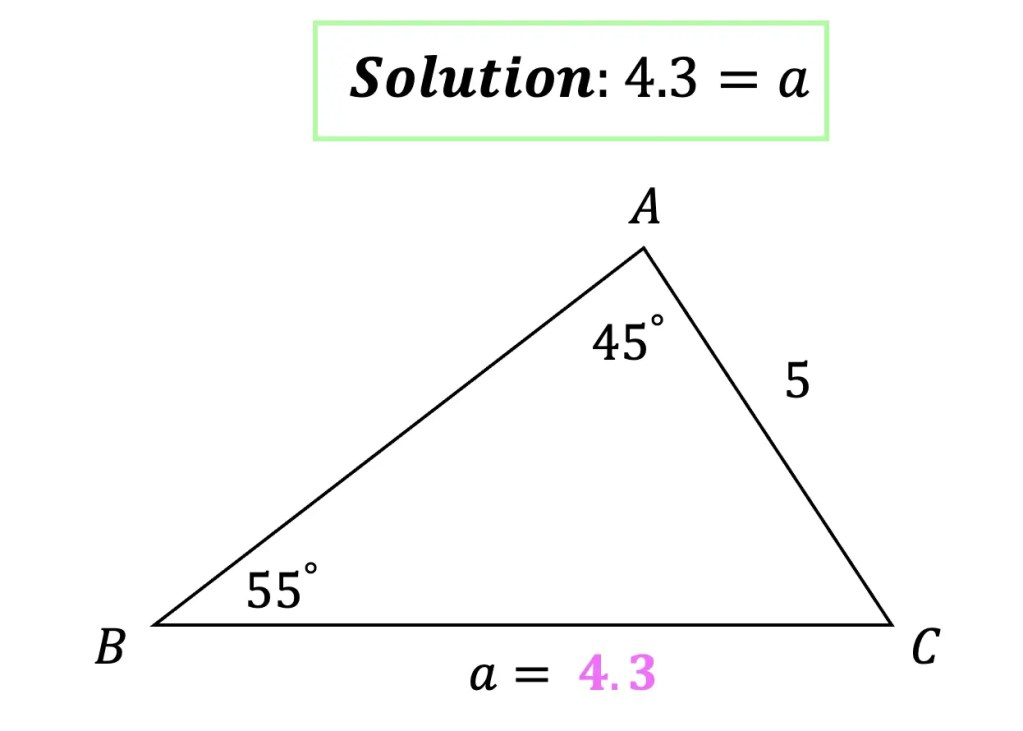
The Golden Ratio is a proportion that is considered to be the most pleasing ratio to the human eye! You may also know the Golden Ratio as the golden mean, the divine proportion, phi, or the Greek letter ϕ. It is an infinite and irrational number that approximates to 1.618 and is found by adding two numbers together and then dividing by the larger number. If these same two numbers are then set equal to the larger number divided by the smaller number successfully, then the two numbers are a golden ratio equal to 1.618! If this sounds too confusing to imagine, just take a look at the formula below:
Is it a Golden Ratio?
If the following formula holds true, then yes there is a golden ratio!

What is amazing about this ratio, is that it can be related back to the Fibonacci Sequence!
The Golden Ration + Fibonacci Sequence:
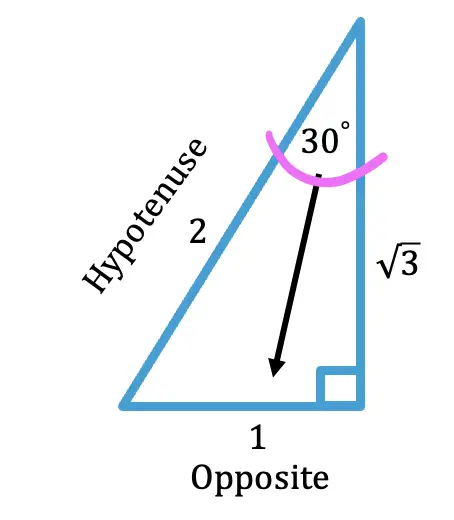
If we were to take the sequential numbers found within the Fibonacci sequence (1,1,2,3,5..), and plug them into the golden ratio formula above, it would approximate to the golden ratio value, 1.618, every time! The the further along we go in the sequence, the closer and closer we get to the golden ratio. Check out with the following examples below:

The Golden Ratio + Art + Architecture + Nature:
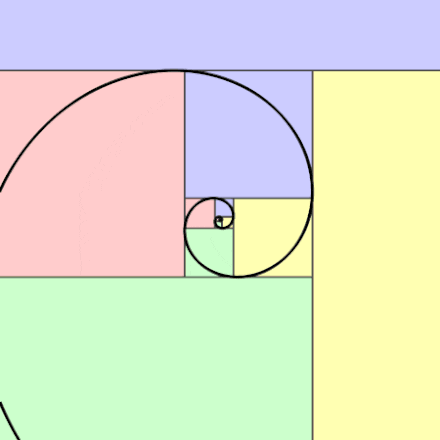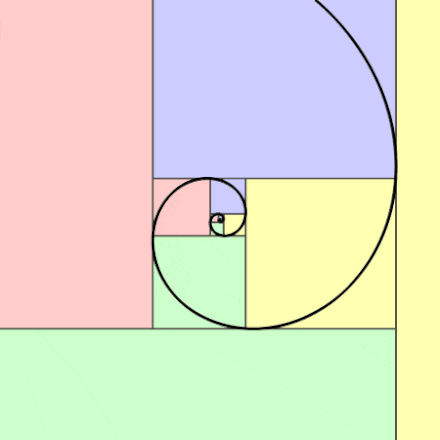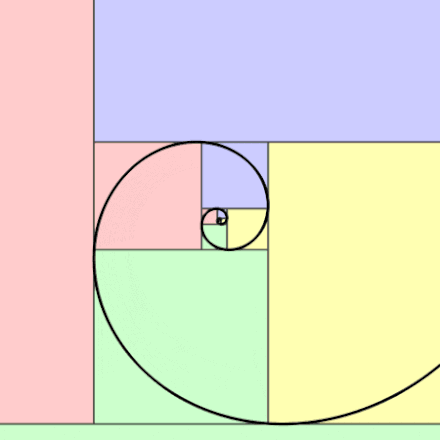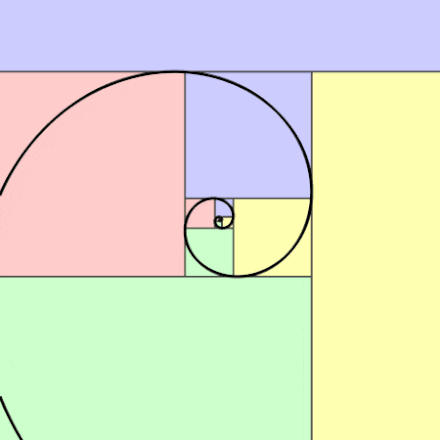
If we were to draw a rectangle that has golden ratio proportions, we would get something that looks like the golden rectangle below.

Now, let’s draw a golden rectangle, within our golden rectangle to see what happens:
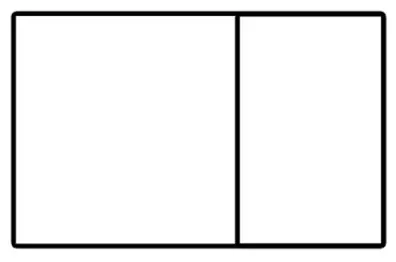
What happens if we continue this specific pattern and keep drawing in golden rectangles within each other?
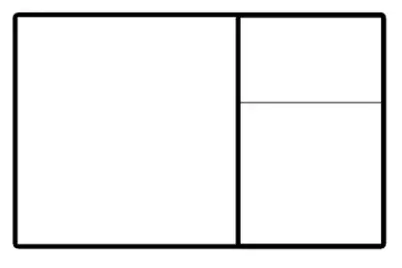
Until eventually we get something like this….
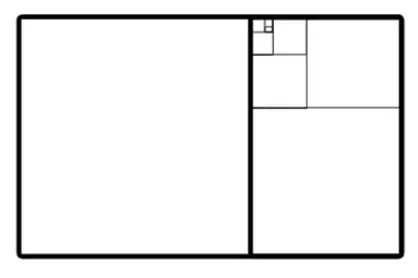
The proportion between the width and height of these rectangles is 1.618 and is a visual demonstration of how the golden ratio is formed with numbers from the Fibonacci Sequence as the sequence approaches infinity.
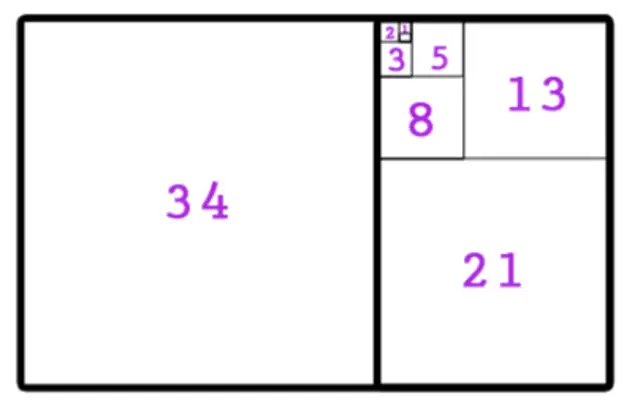
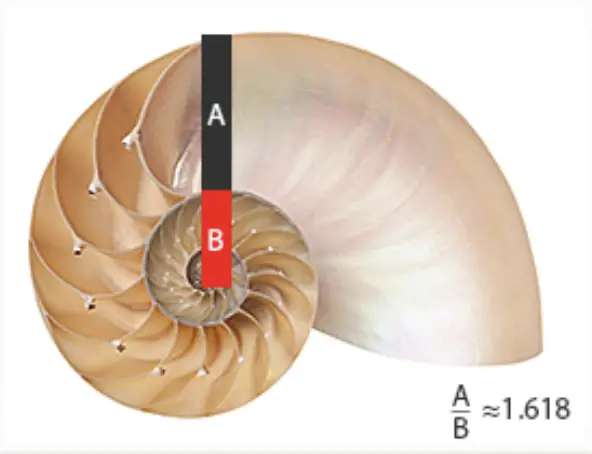
In the above rectangle, when all points of each golden rectangle are connected, something called a Fibonacci spiral (also known as the “golden spiral”) forms. We can see how the golden spiral can be found within the the nature such as the shell shown below and within the architecture of the Taj Mahal.
Also below, we have golden rectangles within the Greek Parthenon architecture and the famous “Mona Lisa” painting by Leonardo DaVinci.

Where can we find The Golden Spiral?
As we mentioned previously, the golden ratio can be found in art, architecture, and nature such as the petals of a flower. Now let’s look at even more examples below:
In nature, we can find Fibonacci spiral within the seeds of the sunflower and the direction in which the aloe leaves grow, shown below:


The Golden Ratio + YOU:
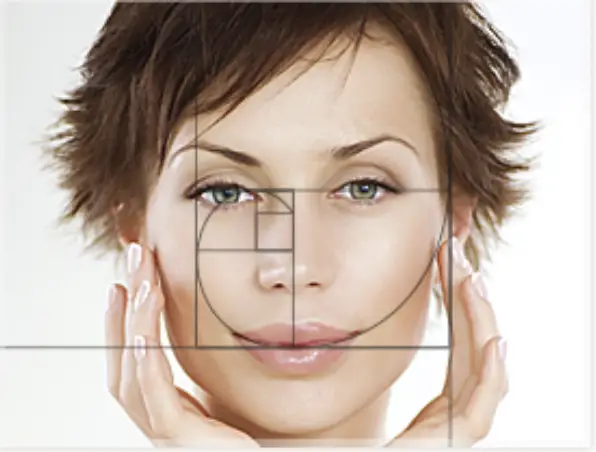
Want to know if you yourself has a face that fits the golden ratio?! Try measuring your face horizontally and vertically and plug in those values into the golden ratio formula, dividing the larger number by the smaller number. What did you get? Something close to 1.6 maybe!? Then you too are a walking example of the golden ratio and the Fibonacci sequence.
Fibonacci and Golden Ratio Resources:
If you’re looking to learn more about the golden ratio and the Fibonacci sequence, be sure to check out the resources I used for this article:
Fibonacci Sequence History: https://www.maa.org/press/periodicals/convergence/fibonaccis-liber-abaci
Rabbit_Problem:http://mathcenter.oxford.emory.edu/site/math125/fibonacciRabbits/
Select Images: https://clevelanddesign.com/insights/the-nature-of-design-the-fibonacci-sequence-and-the-golden-ratio/ and https://giphy.com/
Related Posts:
Looking for more posts on other types of sequences?! Check out these related posts below:
Golden Ratio in the Real World
Still got questions? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂