Welcome MathSux friends! In todays lesson, we will be going over how to find the average rate of change over an interval of a function. This may sound intimidating at first, but all we are really doing is finding the slope, yes, the one we’re already familiar with over an interval given usually in the x-axis. Sounds simple enough? Check out the example below! Also, be sure to watch the video to check out multiple ways for solving these types of problems and the practice problems at the end of this post. Happy calculating!
Average rate of Change over Interval Example:
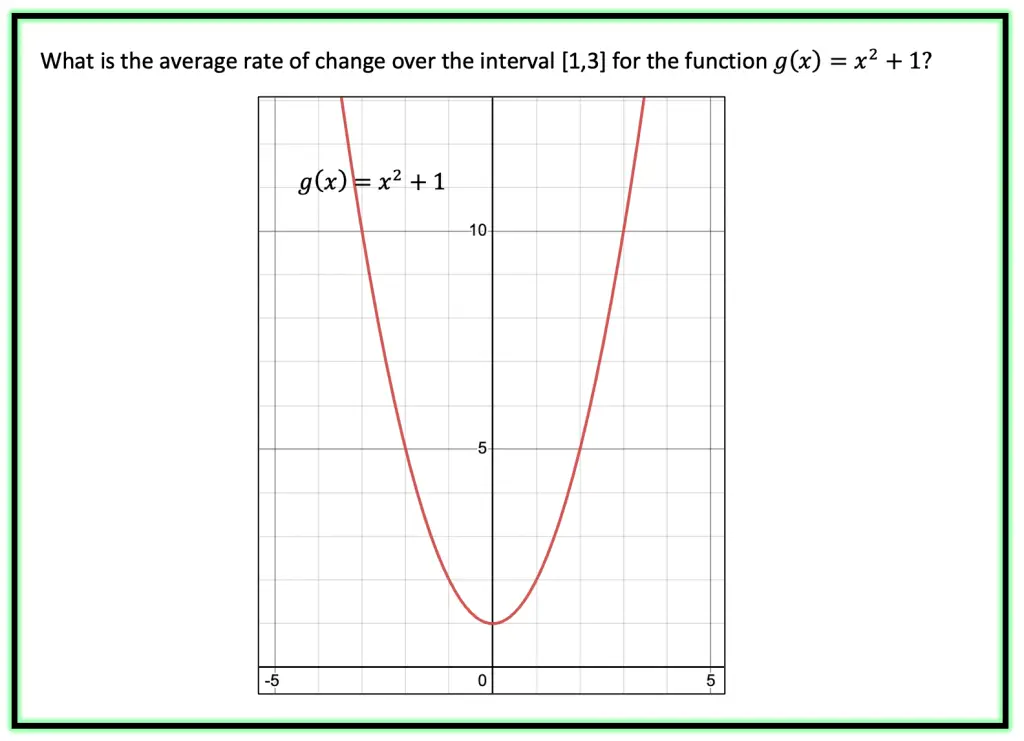
Step 1: The first thing we must do is figure out what this question is saying. The interval, they give us, [1,3] represents the x-values on our graph. So, they want to know what the average rate of change (or slope) is between these two x-values 1 and 3. Let’s take a look and see what that means for us on the graph below!
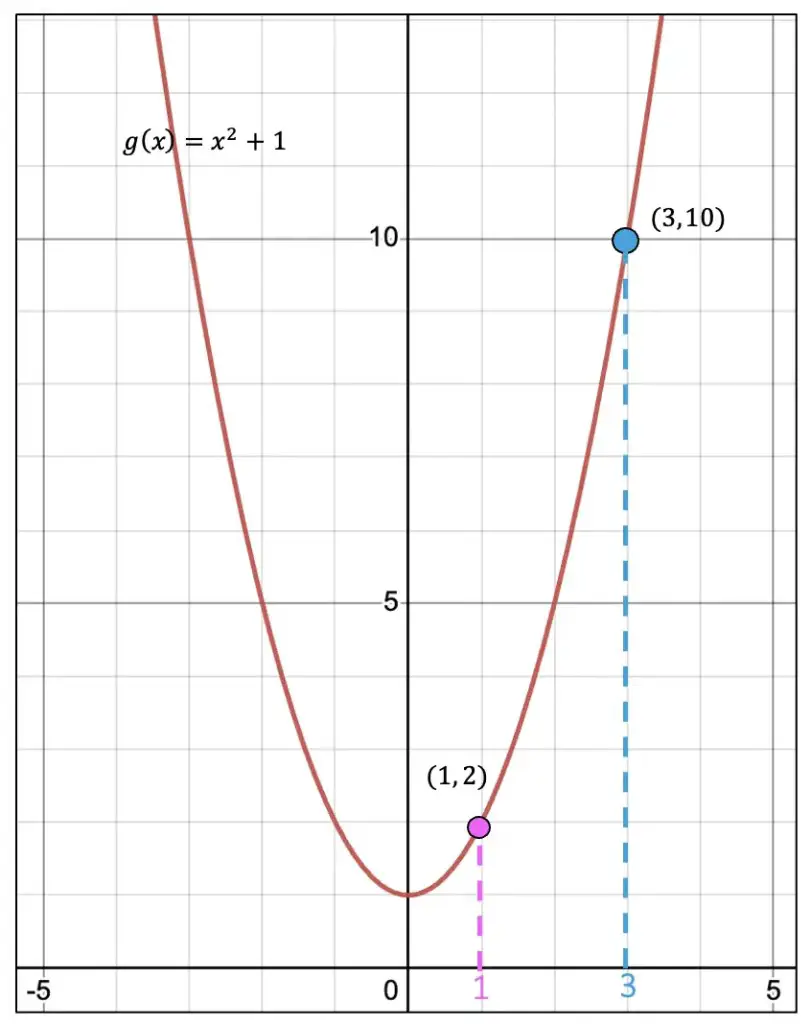
Notice we found the points on our interval [1,3]? This correlates to the coordinate points we will be working with to solve this problem (1,2) and (3,10)
Also, within our interval, [1,3], we will be finding the rate of change (otherwise known as the slope) of the two coordinates (1,2) and (3,10). Check out how we are only finding a small portion of our slope from this function in the diagram below, represented by the dotted green line.
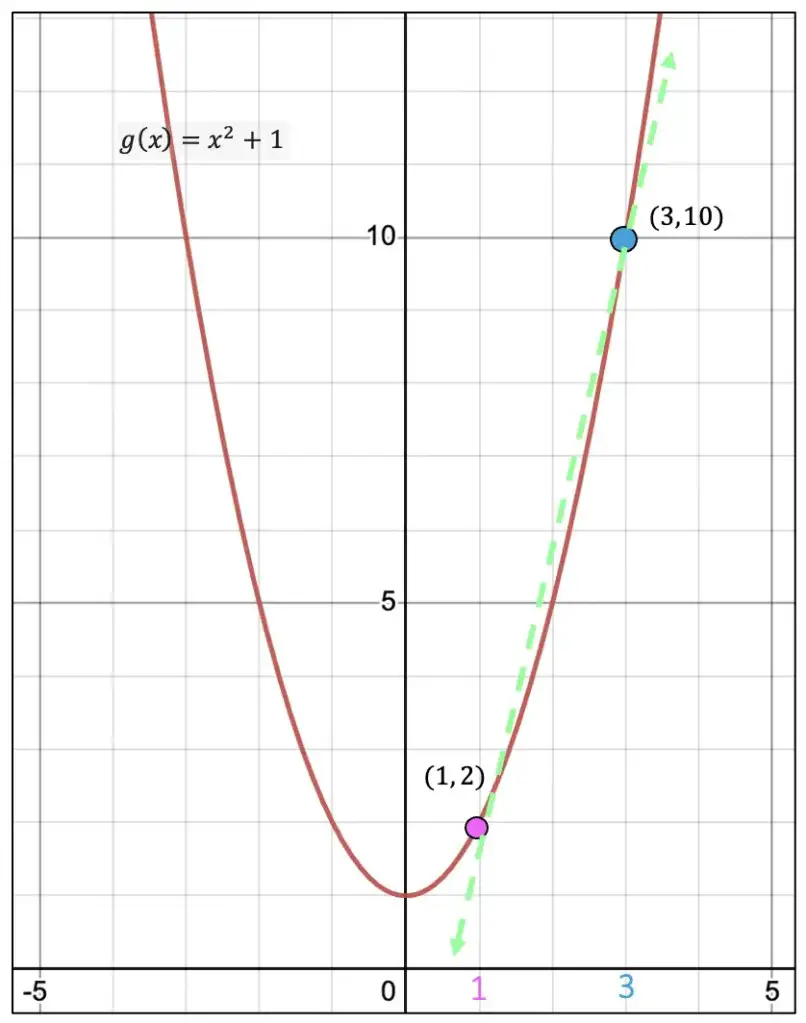
Step 2: Now that we understand what we must do, find the slope within the interval [1,3], using the corresponding points, (1,2) and (3,10), all we must do is plug our numbers into the good ole’ slope formula which we already know!
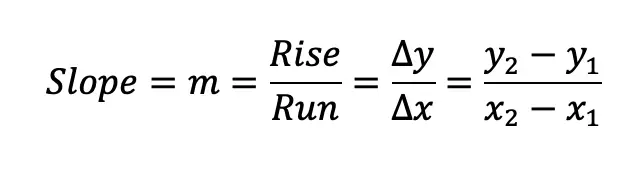
Using our coordinates, (1,2) and (3,10), we can plug in values into the slope formula below:
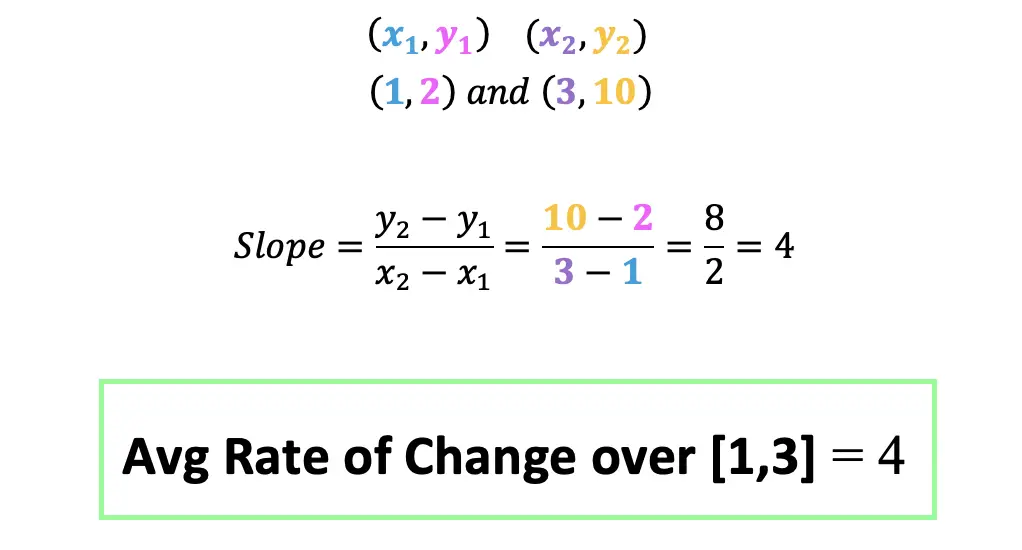
Try the following questions on your own on and check out the video above for more ways to answer this type of question and even more examples!
Practice Questions:
1) Find the average rate of change over the interval [0,2] for the function: h(x) = 2x2 +2
2) Find the average rate of change over the interval [-4,2] for the function: g(x)=(x+3)2
3) Find the average rate of change over the interval [-2,0] for the function: f(x)=-(x+1)3
4) Find the average rate of change over the interval [0,4] for the function: h(x)=x2+2x+1
Solution:
1) 4
2) 1
3) -1
4) 6
Looking to learn more about Algebra? Check out the algebra lessons page here. Thanks for stopping by and happy calculating! 🙂

Wow it’s been a long time