Greeting math friends! In todays post, we are going to be learning how to construct a parallel line using a compass and straightedge. Just a reminder, parallel lines are lines with the same slope and go in the same direction without ever intersecting. Please check out the GIF and step by step tutorial on how to construct parallel lines below. If anything is unclear also don’t forget to check out the video or to comment with any questions! Thanks so much for stopping by and happy calculating!
What are Parallel Lines?
Parallel Lines are lines that have the same slope going in the same direction side by side and never intersect at any point. Ever. Infinitely, keeping the same distance between them. We can also denote that two lines are parallel by using special notation shown in the below example:
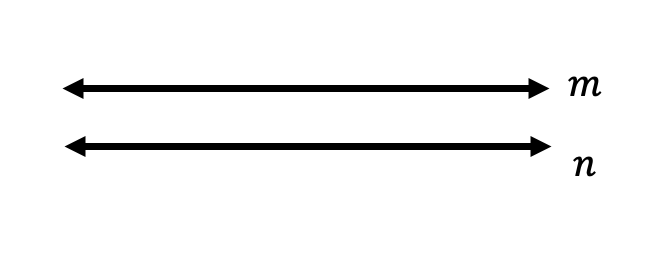
We can say line m is parallel to line n using words or by using the following notation:
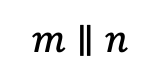
How to Construct a Parallel Line:
Check out the GIF and detailed tutorial below to construct a parallel line given a line and a point using a compass and ruler.

1) Before we begin, let’s take note that we are given line P and Point Q and need to make a parallel line using a compass and straight edge.
2) First, let’s draw a new point anywhere on our original line, line P, and label our new point, point R.
3) Next, using a straight edge or ruler, we are going to draw a line connecting Point Q to new Point R together. Notice we have created a new angle here!?
4) Now, we are going to open our compass to any length, and place the point of our compass on Point R. Next, we are going to swing our compass to create an arc.
5) Keeping that same distance on the compass, now we bring the point of the compass to Point Q, and create another arc.
6) Next, let’s go back to the first arc we made in step 4, and measure the length of our angle using the compass.
7) Keeping that same distance on the compass, measure out the same length on the point where the intersection of the line we created and the second arc we made meet, by placing the point of the compass on this intersection and marking with a dot the angle length.
8) Using a ruler or straight edge, we are now going to connect the point we just made in the previous step, with the original given Point Q to create a parallel line.
9) Check out our parallel line!
*Note in this example, we constructed a parallel line, given continuous line P. But the same construction steps would work with any type of line segment.
Transversals and Parallel Lines:
Why does this construction work in the first place? The short answer is Transversals and corresponding angles! But let’s dive deeper and see why below:
When two parallel lines are cut by a diagonal line ( called a transversal) it looks something like this:
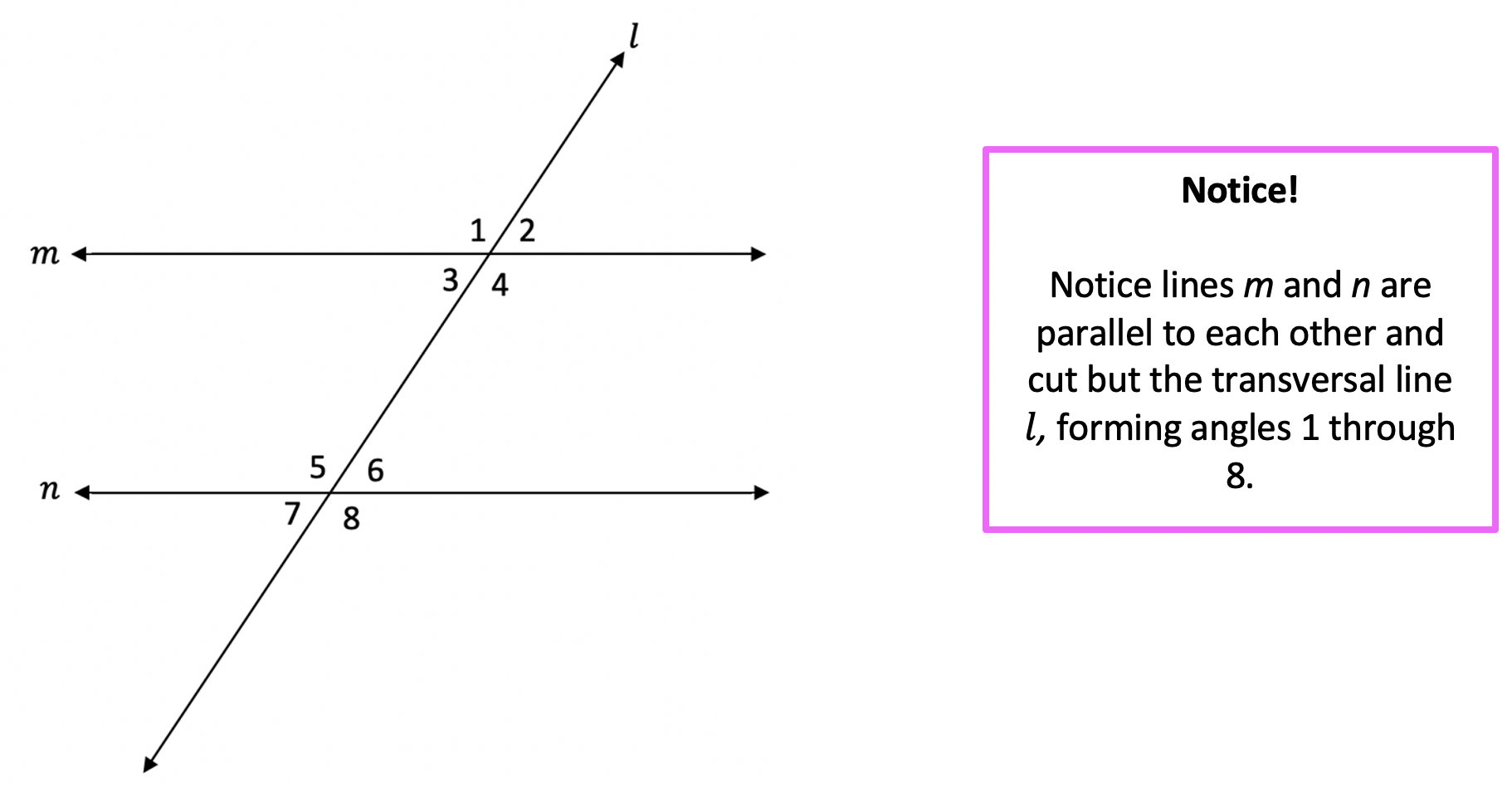
Each angle above has at least one congruent counterpart. There are several different types of congruent relationships that happen when a transversal cuts two parallel lines but for when constructing a parallel line segment, this is due to corresponding angles. For more information, check out this post on Transversals here! And for an example of corresponding angles and how this applies to our proof, keep reading!
Corresponding Angles:
When a transversal line cuts across two parallel lines, corresponding angles are congruent.
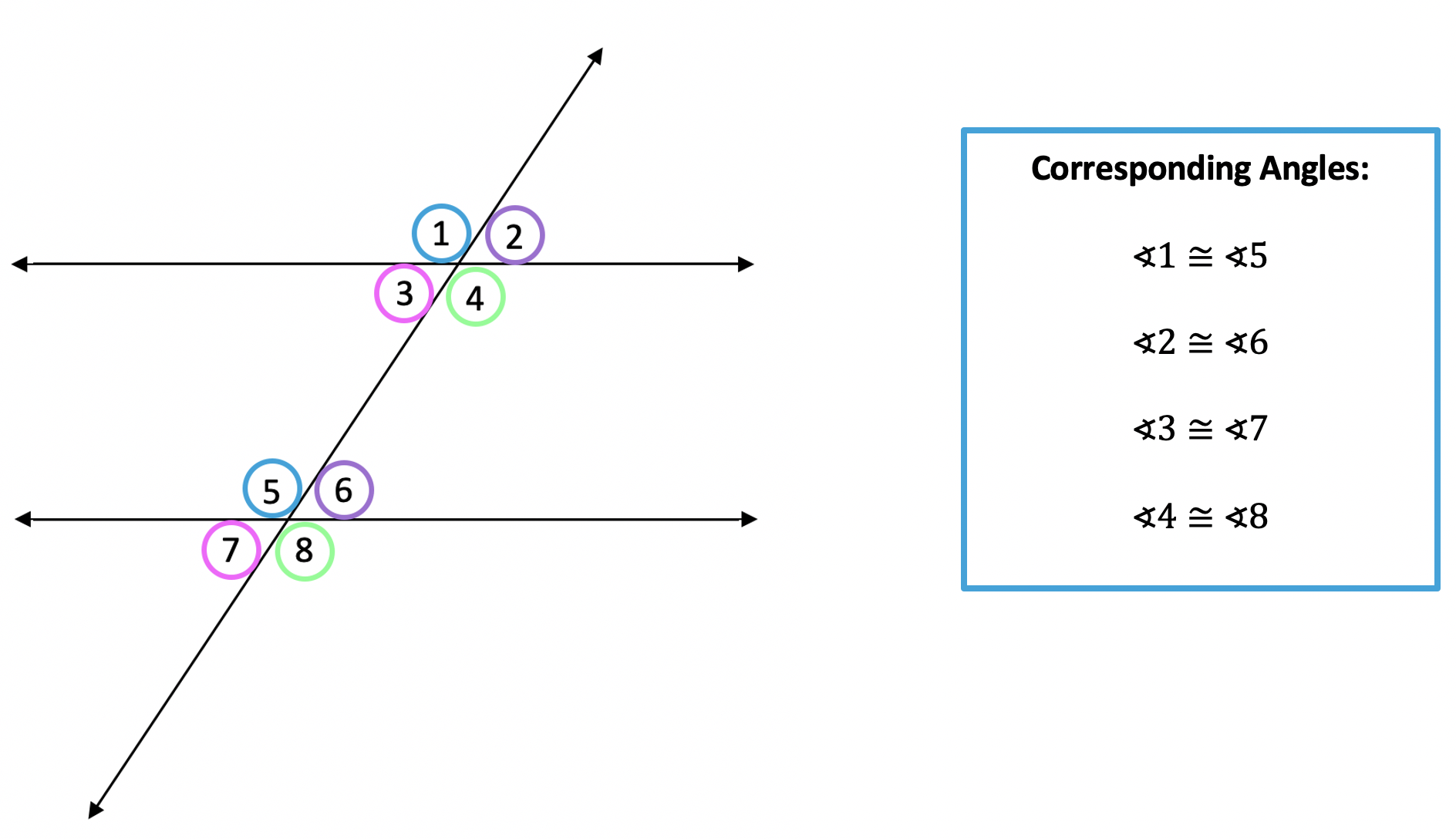
The construction steps to create a parallel line work because of corresponding angles! When lines are parallel and are cut by a transversal, it creates all types of angle relationships including the corresponding angles shown above.
In the construction we did earlier in this post to create parallel lines, if you look back, you’ll notice that we created an angle at angle R and made sure to create a corresponding angle of the same length for angle Q.
Constructions and Related Posts:
Looking to construct more than just a parallel line? Check out these related posts and step by step tutorials on geometry constructions below!
Construct an Equilateral Triangle
Perpendicular Line Segment through a Point
Altitudes of a Triangle (Acute, Obtuse, Right)
Construct a Square inscribed in a Circle
Still got questions? No problem! Don’t hesitate to comment with any questions below or to check out the video above. Thanks for stopping by and happy calculating! 🙂
Let’s be friends! Check us out on the following social media platforms for more practice questions and math examples!
