Hi everyone and welcome back to MathSux! This week we are going to explore how to solve 3 equations 3 unknown. This is like the simultaneous equations we learned to love in Algebra, but now, on steroids. Previously, in algebra we only had to solve for two unknown variables and were given two equations. But now, in Algebra 2, we are faced with three simultaneous equations, as well as, three unknown variables (usually x,y, and z) that we must find the values of. These types of problems can look scary, but with the method of elimination and some practice, they are not so bad! Check out the video, step by step tutorial, and practice problems below to master this topic. Good luck and happy calculating!
What are 3 Systems of Equations with 3 Unknown Variables?
Three systems of equations happen when there are three equations (usually with three unknown variables) are graphed or shown algebraically. The graph can be represented by using the variables x,y,z (one for each of the three missing variables). We are all used to the 2-dimensional coordinate plane with X going across and Y going up and down. But now, with a new unknown variable, z, this gives us a new 3-dimensional axis. Instead of graphing lines like we are used to, these equations are going to be graphed as 3-dimensional planes.
As for finding the solution to a system of three equations, it is the same for any simultaneous equation, as the answer lies where all three planes intersect. Below is an example of what a three-dimensional plane can look like when graphed. Don’t worry, typically you wont be asked to graph or even interpret anything like the picture below.
Instead of graphing, typically we are asked to find the solution using algebra! There are three equations and three unknown variables. How are we supposed to know and find the value for each variable? Well, there are more than one way to solve these types of problems, but in this blog post and in the video above, we will be going over the elimination method. This is the fastest and easiest way to solve for 3 unknown variables by hand.
Solving by Elimination
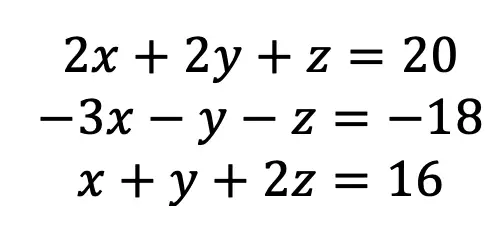
The main idea of Elimination is to pick two pairs of equations and add them together with the goal of canceling out the same variable. We do this by lining up both equations one on top of the other and adding them together. If a variable or variables does not easily cancel out at first, we then multiply one of the equations by a number so it will cancel out.
For example, adding the first equation (2x+2y+z=20) and second equation (-3x-y-z=-18) will quickly cancel out z. When we pick another pair of equations to add, picking the second equation (-3x-y-z=-18) and the third equation (x+y+2z=16), we will also have to goal of canceling out z. Once z has been eliminated twice, it provides us with an opportunity to add together the two new equations we just found and eliminate even further to find the value of each unknown variable. If this sounds like a confusing mouthful, do not worry! We’ll go over this process step by step below.
Check out how it’s done step by step below!

Step 1: First, let’s take another look at our equations and number them so we can keep track of which equations we’re using and when.
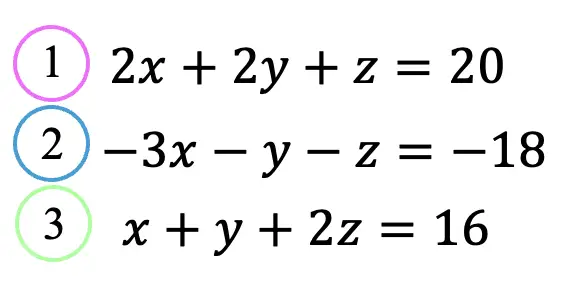
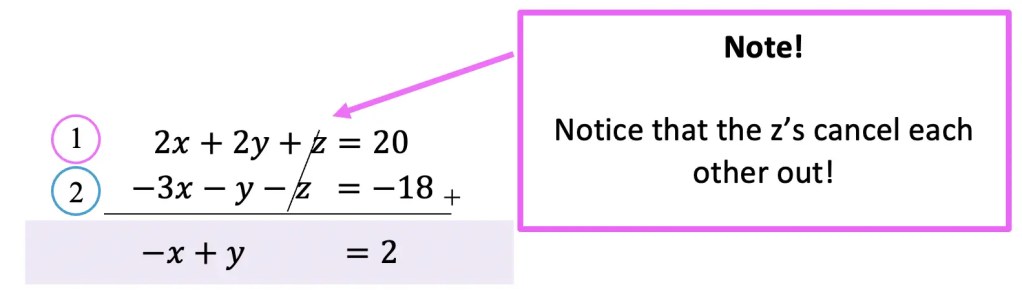
Step 2: Now let’s pick two equations and try to eliminate one of the variables. If we look at the first two equations (labeled 1 and 2) above, notice we can easily cancel out at the unknown variable z.
Step 3: Ok great, what now? Now we are going to take a different pair of our original equations and have the same goal of canceling out the same unknown variable z (just like we did in in the previous step). Let’s pick the last two equations from above, (labeled 2 and 3). Notice that these two equations do not easily cancel out unknown variable z, therefore, we must multiply 2 times the whole of equation 2 so that they do cancel each other out.
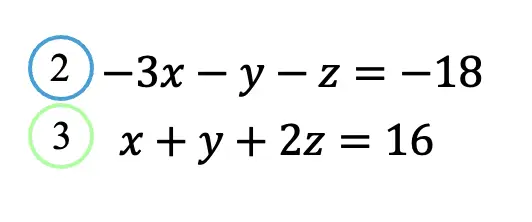
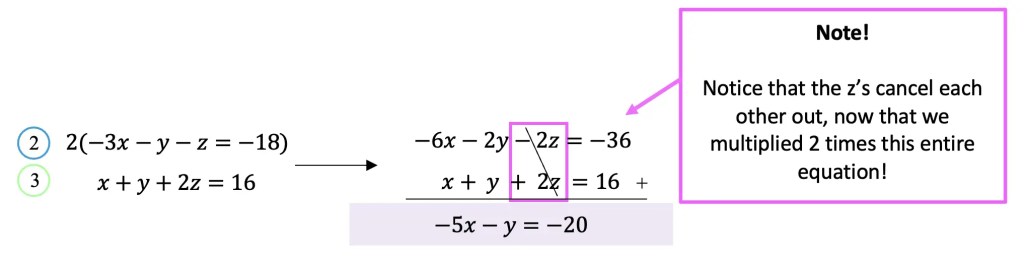
Step 4: Now, that we’ve canceled unknown variable z from two different pairs of equations, we can use the two new equations we found in steps 2 and 3 (hi-lighted in purple) to cancel out another variable.
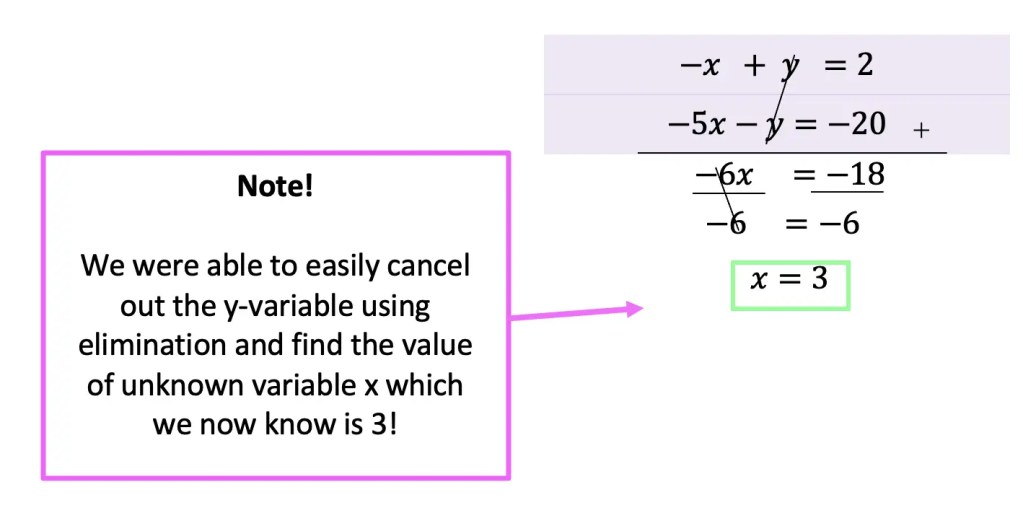
Step 5: Now that we have the value of one variable, x=3, we can plug it into one of our equations that we used in step 4.
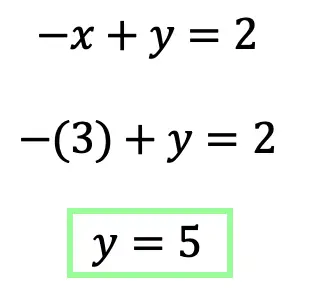
Step 6: Last but not least, let’s find the value to our last unknown variable, z, by plugging in x=3 and y=5 into one of our original equations at the beginning of this example.
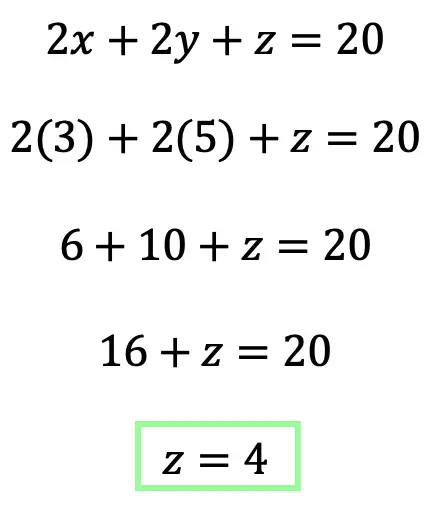
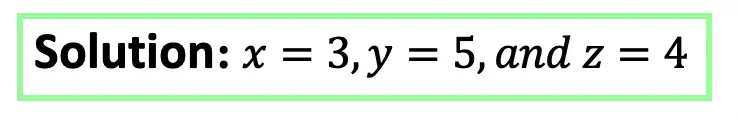
Was the wording a bit much? Too many things!? Don’t worry, check out the video and see how this questions gets worked through step by step on a piece of paper. And, if you get the example above, please check out the practice questions below!
Practice Questions:
Find the values of each three variables for each system of equations:

Solutions:

Want more MathSux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating!
Facebook ~ Twitter ~ TikTok ~ Youtube
*Bonus* Are 3 equations 3 unknown variables at the same time too much to handle? Check out how to find two simultaneous equations here!


One thought on “3 Equations 3 Unknown”