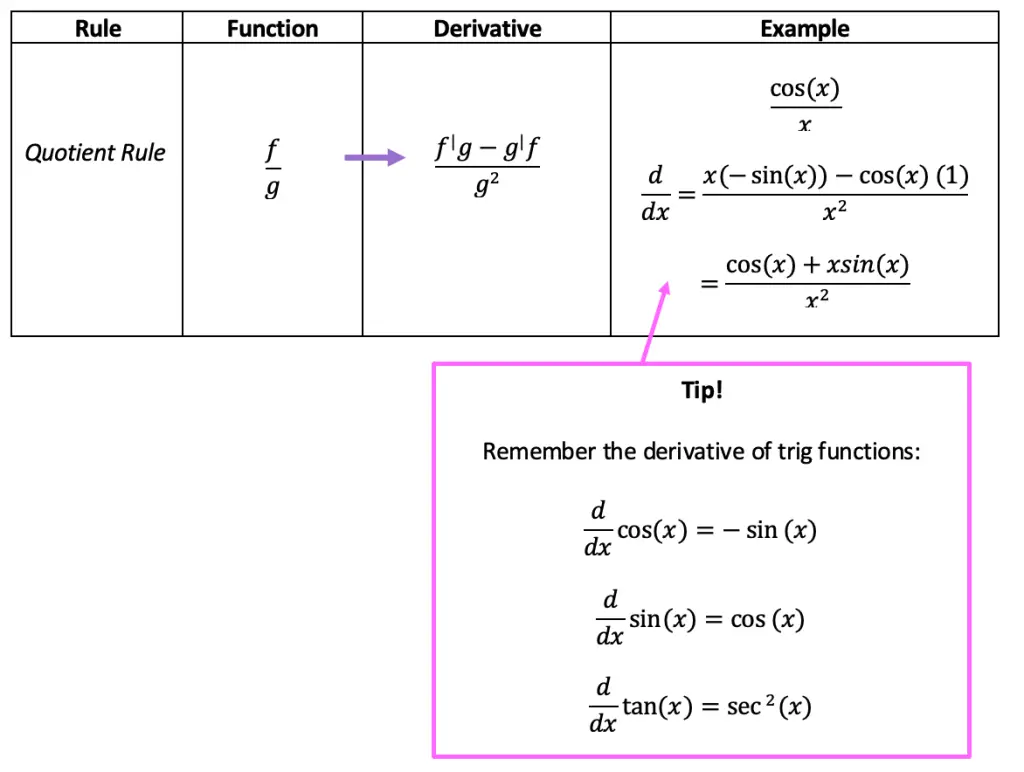
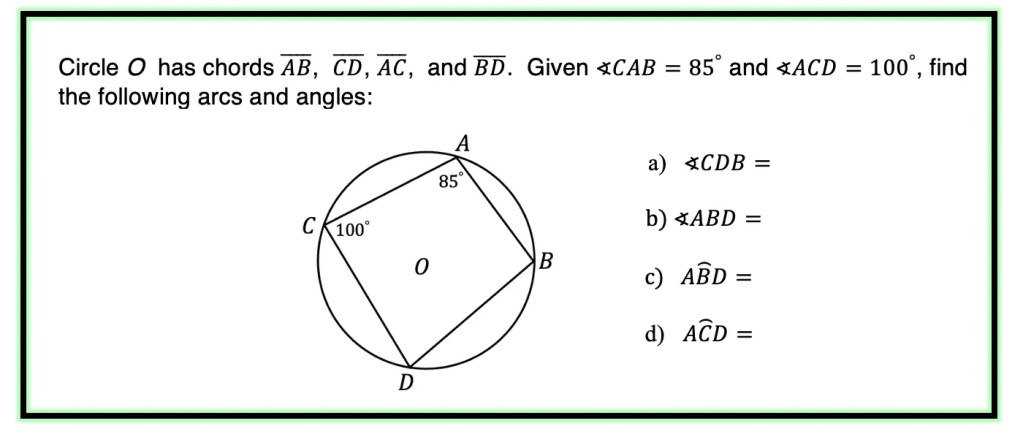
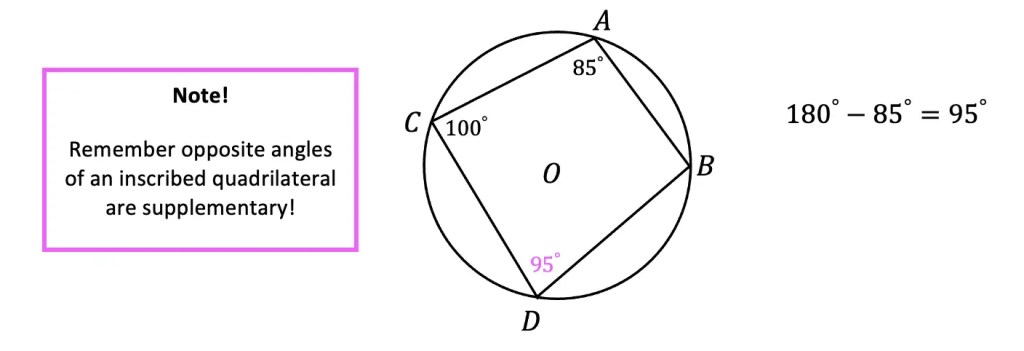
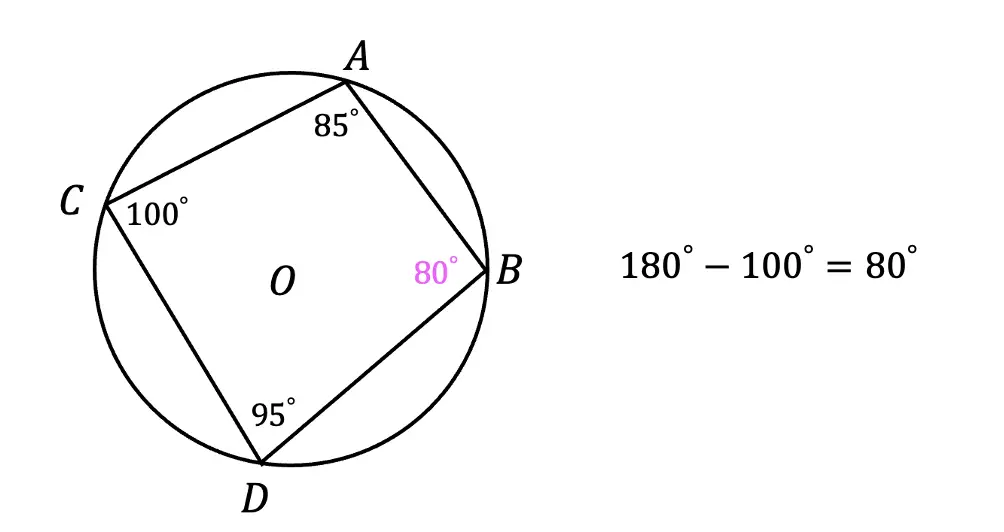
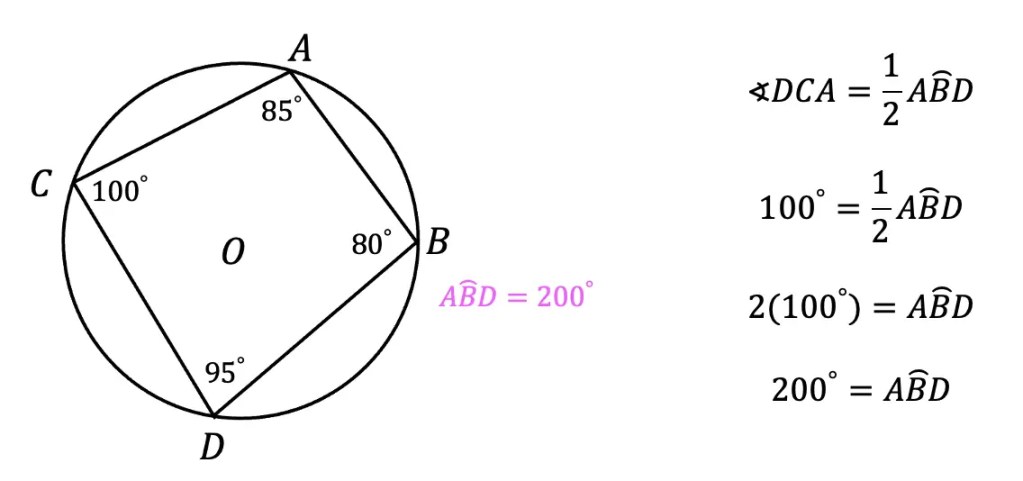
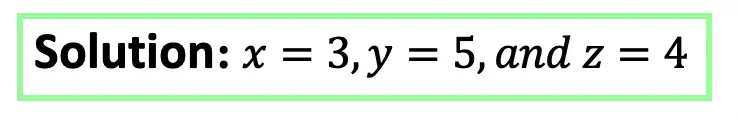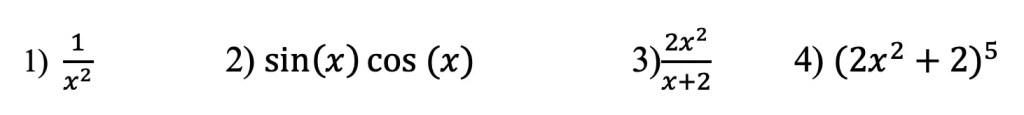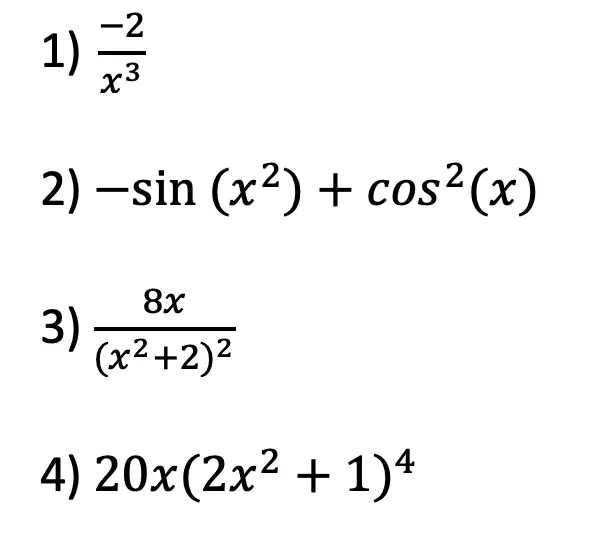Greeting math peeps and welcome to MathSux! In today’s post, we are going to have a bit of fun when finding the volume of a cube. We’ll start by going over how to make a paper cube using origami, then we will measure the dimensions of our real-world cube and find its volume. Hope you’re all feeling crafty and ready to take on this project with the Japanese art style of origami! If you don’t have any origami paper, please fill free to print out the origami guideline sheets included at the end of this post to follow along! Also, if the below written tutorial isn’t your style, watch the video up on YouTube and shown below. Hope you’re all having a great week and can find some fun in this post! Happy calculating!
How to Make a Paper Cube Using Origami:

Step 1: Begin with six sheets of square origami paper (or cut out a square from any type of regular computer paper). If you want to really follow along, this paper is 4 inches by 4 inches and I have included a print out below.

Step 2: Fold the top of the origami paper in half, then unfold.

Step 3: Fold one side of the paper halfway to the center.

Step 4: Fold the left side to the center of the paper and rotate the paper horizontally.

Step 5: Take the bottom right corner and fold it to the top center point of the rectangle.

Step 6: Now fold the top left corner and bring it to the bottom edge, so both folds align in the middle.

Step 7: Next, Open both folds towards the center, undoing our last two steps.

Step 8: Open the first flap on top, and fold in the top right triangle.

Step 9: Unfold the bottom flap, and fold in the bottom left triangle.

Step 10: Now, we are going to fold down the top left corner to the center of the paper (just above the bottom flap).

Step 11: Fold up the bottom flap.

Step 12: Now take the bottom right corner, and tuck it in under the top flap, towards the center.

Step 13: Flip your piece of paper around.

Step 14: Fold the corner, towards the center.

Step 15: Now, fold in the bottom left edge, towards the center, to the top edge.

Step 16: Unfold, the left and right edges we made to get a shape like we have above.

Step 17: Repeat steps 1 through 16 5 more times! To have a total of six of the above shapes. We will need all of them to piece together our origami cube.

Step 18: Connect each of our shapes, by placing the edge of each in top left the corner “pocket” of each shape.

Step 19: Once they are all connected, we finally have created our origami cube!
Print out Origami Paper:
Want to follow along with everything!? Check out the printable origami paper below to create your very own box!
Volume of a Cube:
Now that we have made our cube using paper folding, we can measure one side of our cube and find its volume! Please note that these measurements are based on the 4″X 4″ origami paper I used. If you would like to follow along with your own project, just download and print the activity sheet above!

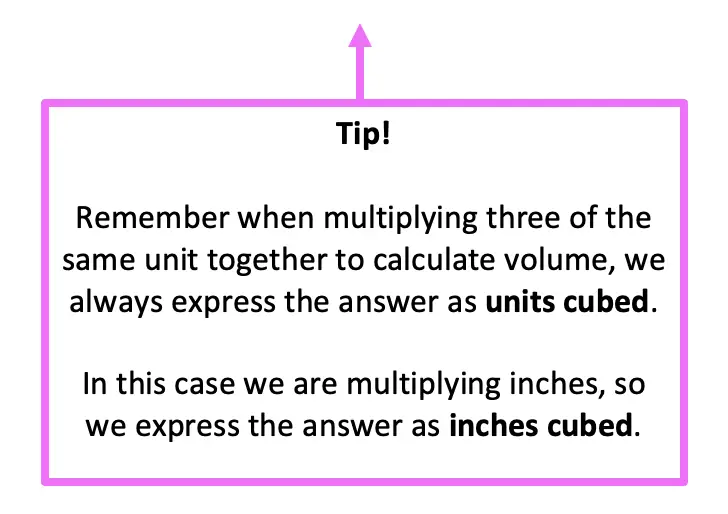
Did you create your origami cube with different-sized origami paper? Let us know what measurement you got for volume in the comments below!
Looking for more Origami + Math? Check out this post here to fold and find the volume of a real-world pyramid and rectangular prism. And for another math + crafty post, learn how to make a Mobius Band here!
What is your favorite way to combine math and the real world? Or math and art in general? Let me know in the comments and happy calculating!
Facebook ~ Twitter ~ TikTok ~ Youtube
Looking for another math challenge? Check out this post on derivatives here!