Greeting math peeps! Today we are going to talk about translation math in reference to transformations and geometry! Translations are a type of transformation where we take a point, line, or shape and move it up, down, left, or right on a coordinate plane. A shape retains its angles, lengths, and direction after a translation, all we are doing is simply moving it around the coordinate plane. Think you are ready to master the topic!? Keep reading for more explanation, video lesson, and step by step examples. Happy calculating!
Translations Math Formula:
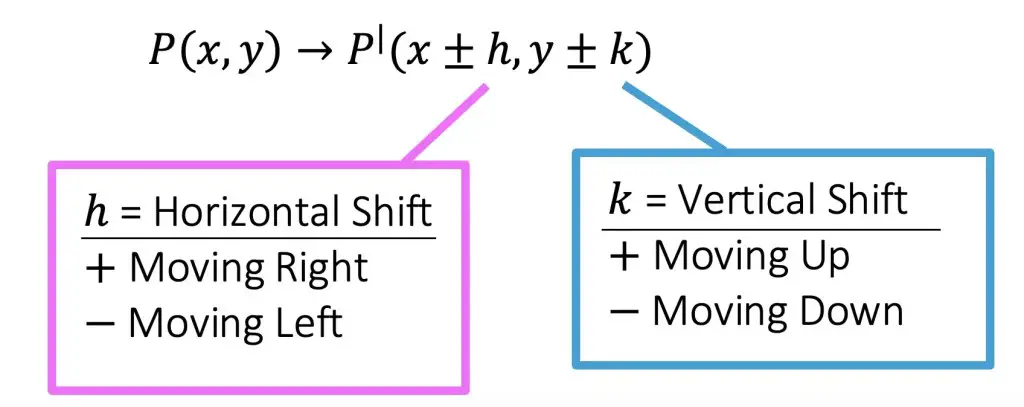
P(x,y) -> P| (x+h, y+k)
where….
h=Horizontal Shift (add (+) when moving right, subtract (-) when moving left)
k= Vertical Shift (add (+) when moving up, subtract (-) when moving down)
What are Translations?
Translations are a type of transformation in geometry where we take a point, line, or shape and move it up, down, left, or right on a coordinate plane. Let’s take a look at what a translation looks like below.
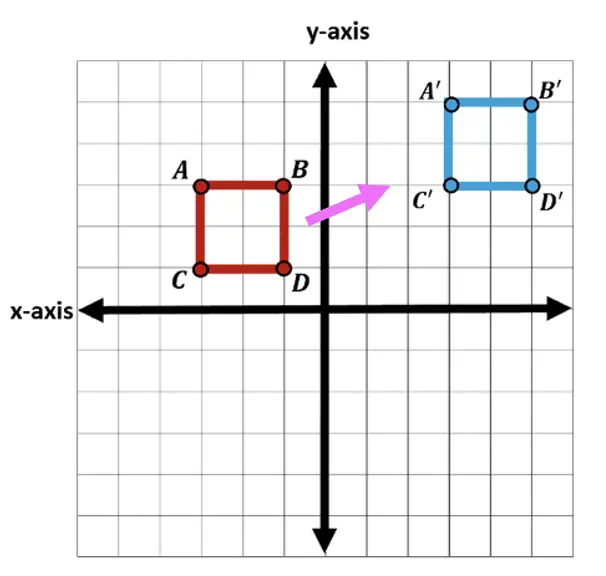
In the translation example above, we go from square ABCD to square A|B|C|D| translating each coordinate of the original square 6 units to the right and 2 units up.
Properties of a Translation + Rigid Motion:
When a shape, line, or point is translated, the shape retains Rigid Motion, meaning its length, area, and angles are unaffected by the transformation, as well as, maintaining its same direction.
- Angle values remain the same.
- Parallel and perpendicular lines remain the same. (shape/line maintains same direction)
- Length, area, and perimeter remain the same.
There are two main types of translations: horizontal translations and vertical translations, let’s take a look at what each mean below.
Horizontal Translation:
When we translate a point, line, or shape left or right, it is undergoing a horizontal translation along the x-axis. Any type of left or right movement on a coordinate plane is a horizontal translation.
How does this affect the x-coordinate? If the shape is being translated to the right, then we are adding units to the x-coordinate, and if the shape is shifting left then we are subtracting units from the x-coordinate.
Vertical Translation:
When we translate a point, line, or shape up or down, it is undergoing a vertical translation along the y-axis. Any type of up and down movement on a coordinate plane is a vertical translation.
How does this affect the y-coordinate? If the shape is being translated up, then we are adding units to the y-coordinate, and if the shape is being shifted down then we subtract from the y-coordinate.
Even though a horizontal shift or a vertical shift can happen when we move a shape, line, or point, many translations have a combo of the two!
How do Coordinates Change after a Translation?
The truth is there is no one unique rule for translations, but numbers will always be added or subtracted from the x and/or y coordinate values. If something is translated to the right, then we add units to the x-value. On the other had if something is translated to the left, we subtract units from the x-value. The same can be said for moving a shape up, we then add units to the y-value, and if a shape is translated down, we subtract units from the y-value. This gives us the following translation formula below:
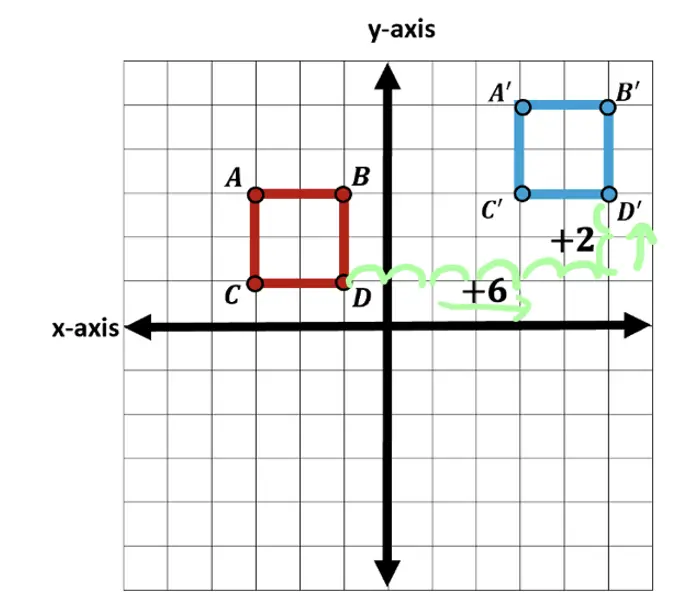
If we look at our example, when we translate original square ABCD to square A|B|C|D| we end up translating each coordinate of original square ABCD 6 units to the right and 2 units up. What we are really doing when we translate is adding 6 units to each x-coordinate as well as adding 2 units to each y-coordinate of the original figure square ABCD. Check it out below:
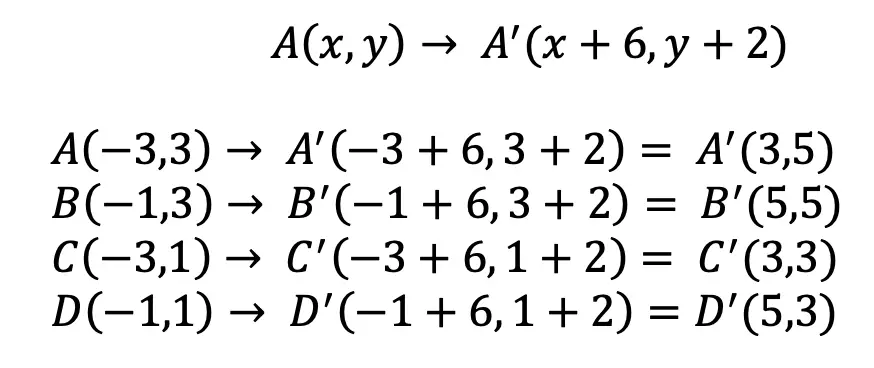
Now that we understand more about translations, let’s jump into some examples!
Translation Math Examples
Example #1: Translating Triangles
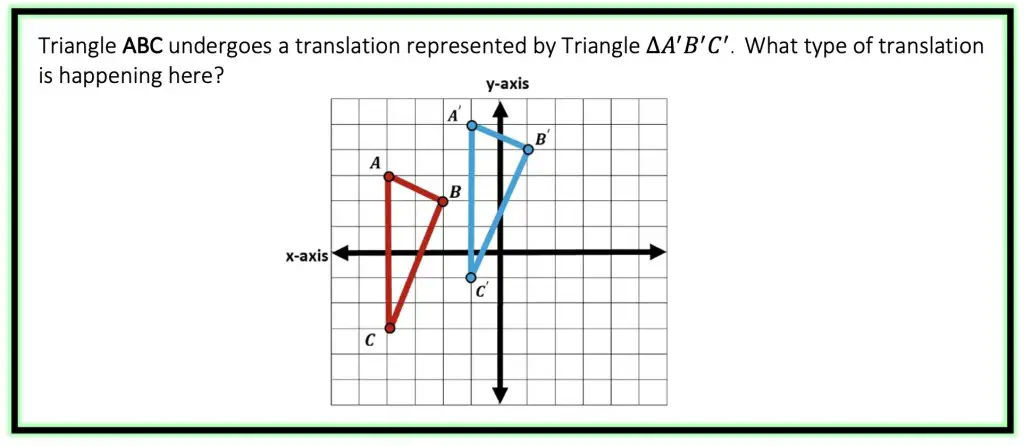
The Game Plan: To solve this problem, we’re going to need to compare two corresponding coordinate points before and after the translation. We can look at any of the following pairs to find our answer A & A|, B & B|, C & C|. Still confused? If so, no worries, because we will take this step by step!
Step 1: Identify a pair of coordinates to compare before and after the translation. In this case we compare Points A and A|.
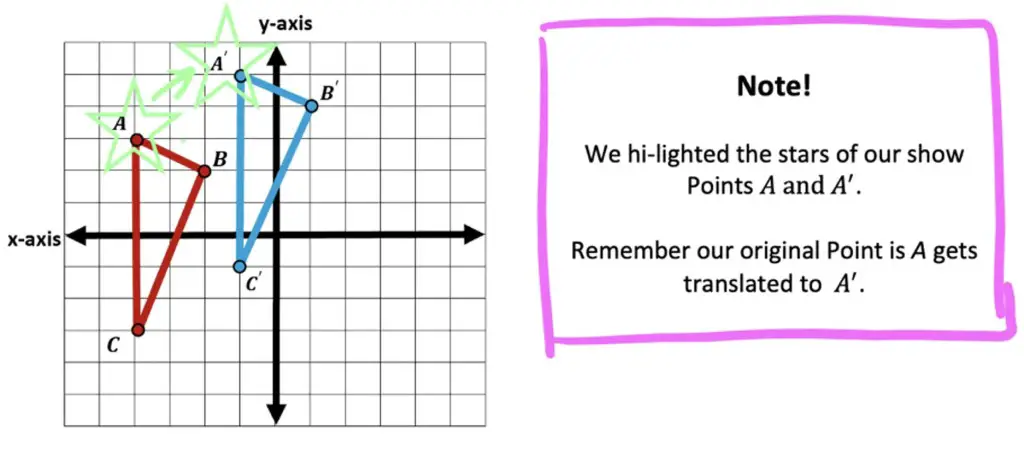
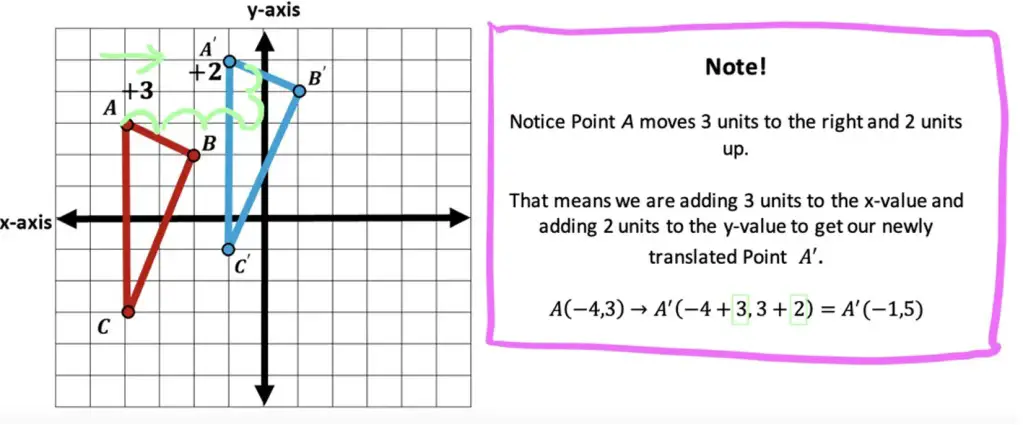
Step 2: Now we need to measure how many units to the right and how many units up Point A| is from Point A.
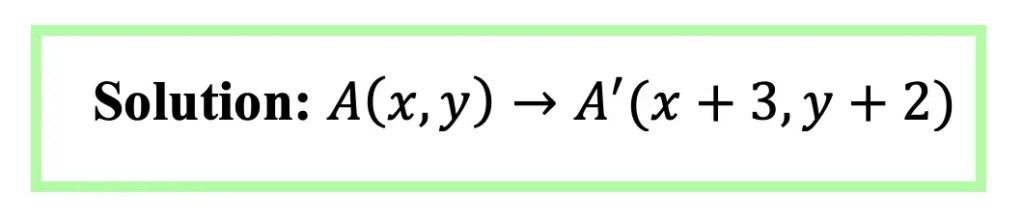
We’ve gone over translating shapes, alas, shapes aren’t the only things that can be translated. Fun surprise: lines can be translated too! The same rules apply to translating lines as they do to shapes. The nice thing about translating a line vs. a shape is that we now have even less work to do (as there are less points to translate).
Example #2: Translating Lines
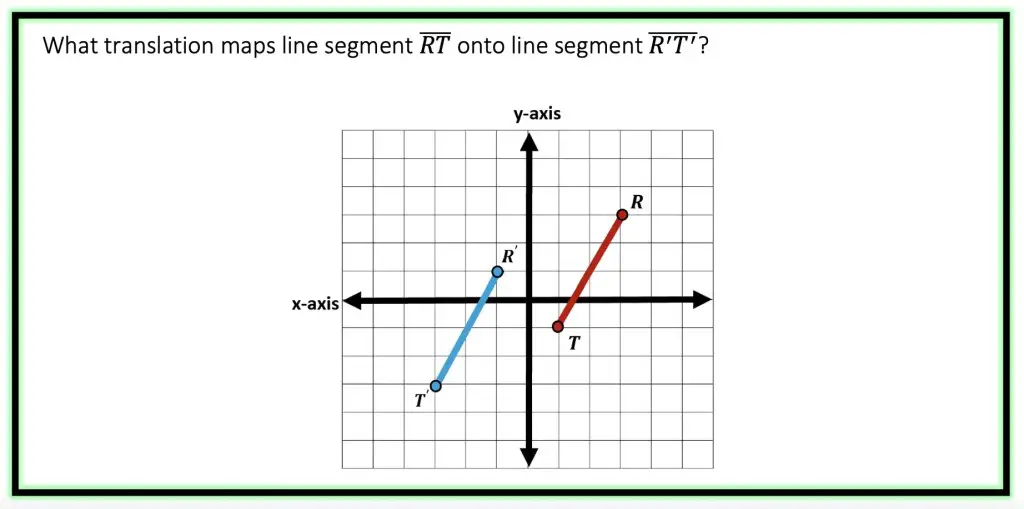
The Game Plan: This question is asking us to find the translation from line RT to line R|T| . We’re going to need to compare corresponding coordinate points before and after the translation. We can look at a set of points before and after the translation including Point R & R| or Point T & T|. Nothing we can’t handle! Let’s do this!
Step 1: Identify a pair of corresponding points before and after the translation, for this problem let’s focus on Point R and Point R|.
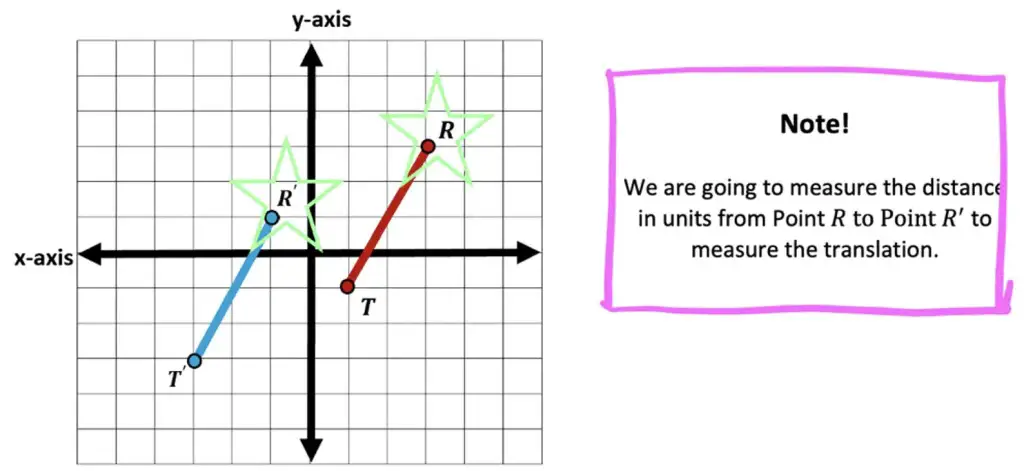
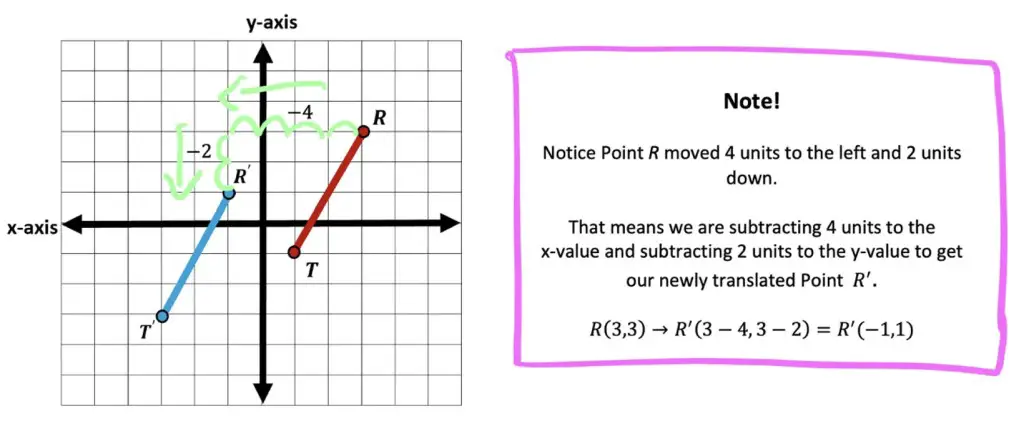
Step 2: Now we measure how many units to the left and how many units down Point R| is from Point R.

Practice Questions:
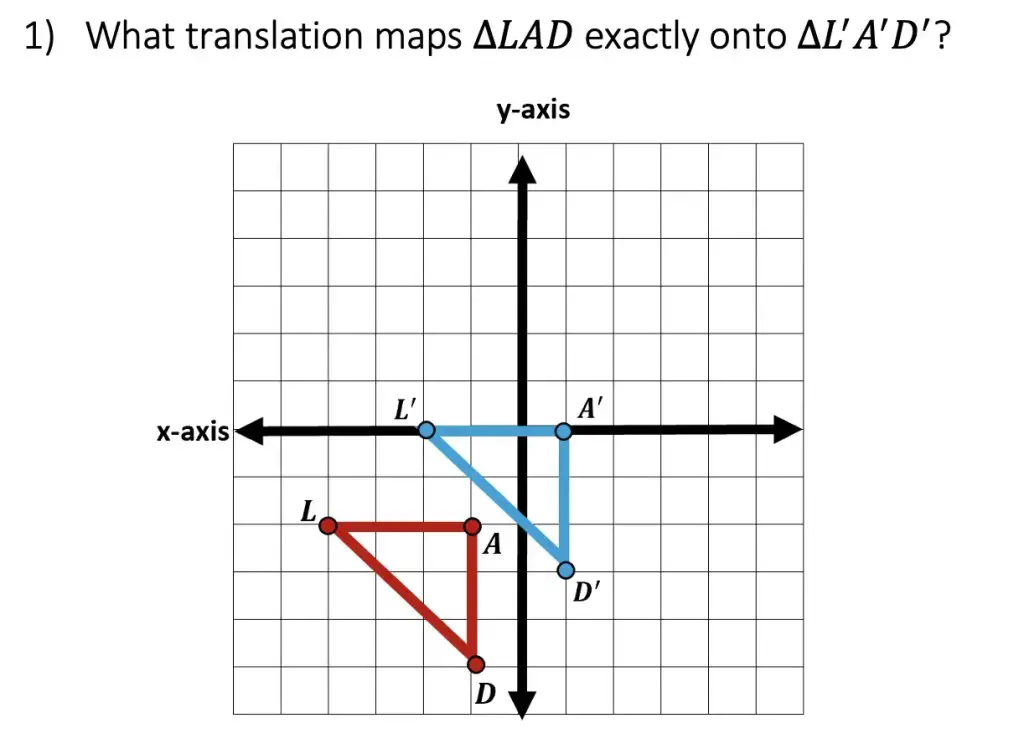
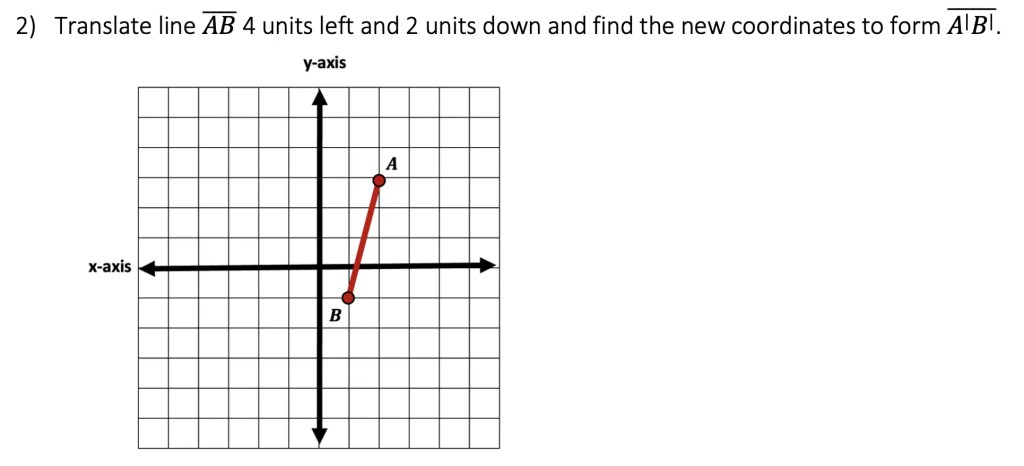
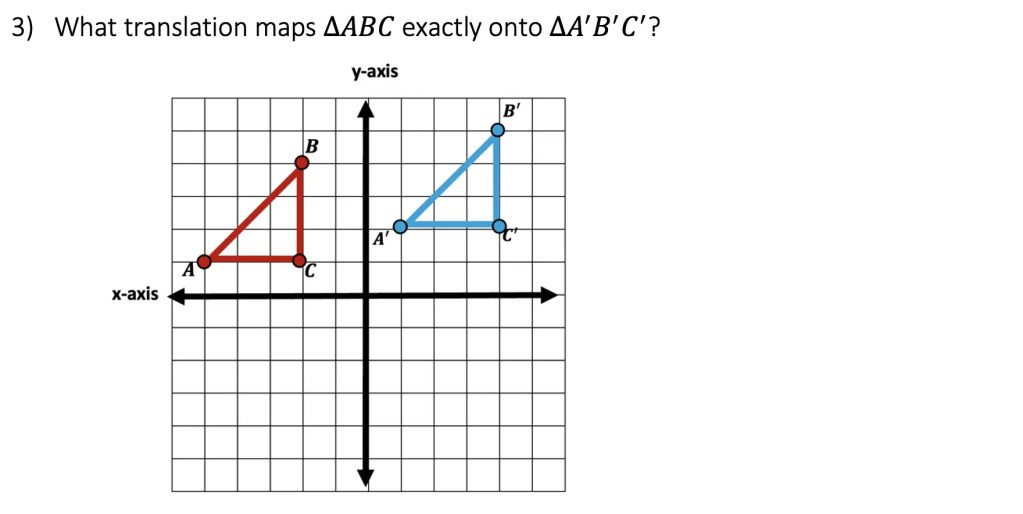
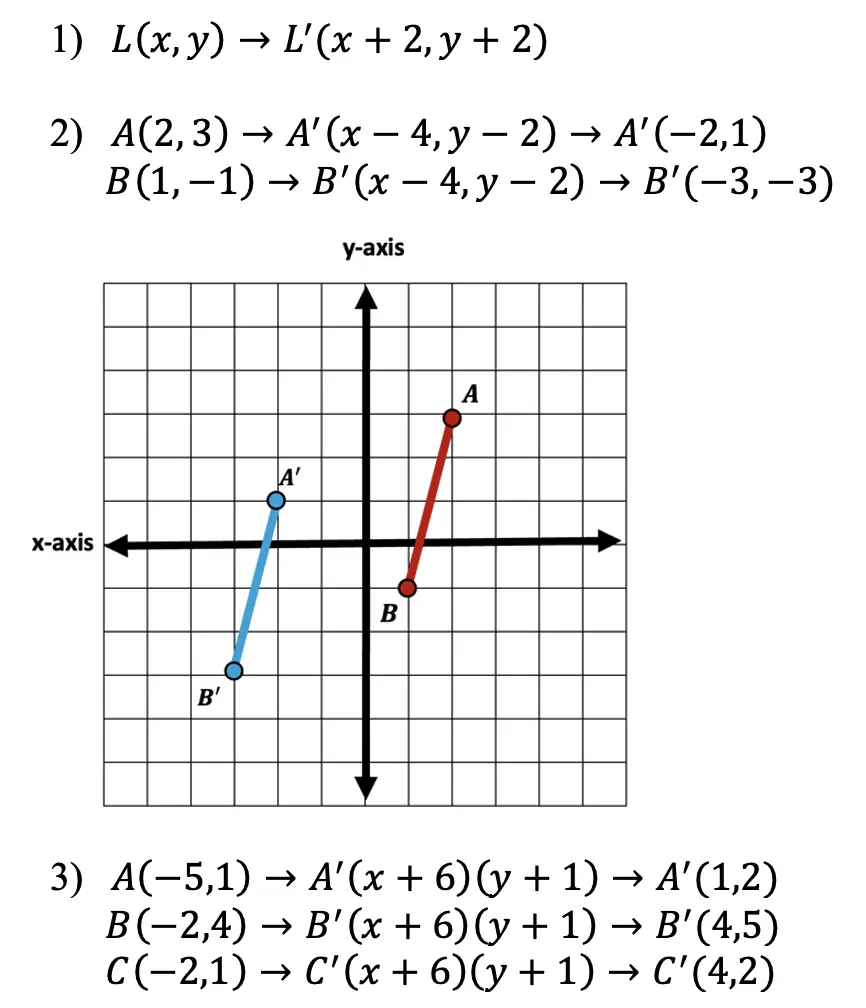
Solution:
Other Transformations:
If you’re looking for more Transformations other than on the translation math you see here, check out these lessons below! Or, click this link here!
Also, be on the lookout for the latest MathSux lessons and study tips on Twitter, Facebook, YouTube, and TikTok! Happy calculating!
Translation math
Facebook ~ Twitter ~ TikTok ~ Youtube

3 thoughts on “Translation Math”