Hi everyone and welcome to another week of MathSux! In today’s post, we are going to go over all the different types of shape transformations in math that we’ll come across in Geometry! Specifically, we’ll see how to translate, reflect, rotate, or dilate a shape, a line, or a point. There are also specific coordinate rules that apply to each type of transformation, but do not worry because each rule can also be easily derived (except for those tricky rotations, keep an eye out for those guys!). If you like art or drawing, this is a great topic where we’ll have to use our artistic eye and our imagination for finding the right answer. We’ll also take a look at where you might use and see transformations in your everyday life! Hope you are ready, take a look below and happy calculating! 🙂
What is a Transformation in Math?
Mathematical Transformations, include a wide range of “things.” And by “things” I mean reflections, translations, rotations, and dilations; Each fall under the umbrella known as “transformations.” Alone any one of these is not difficult to master but mix them together and add a test and a quiz or two and it can get confusing. Even the words “transformation “and “translation” can get confusing to us humans, as they sound very similar. But these are two different things. A translation is a type of transformation. Let’s break down each of our new words before our brains explode:
Transformations: When we take a shape or line and we flip it, rotate it, slide it, or make it bigger or smaller. Basically, when we have a shape or line and we mess around with it a bit, it is a transformation. The shape or line in question is usually graphed on a coordinate plane. Transformations include:
(1) Translations (slide it)
(2) Reflections (flip it)
(3) Rotations (rotate it)
(4) Dilations (make it bigger or smaller)
Shape Transformation:
1) Translations – When we take a shape, line, or point and we move it up, down, left, or right.
2) Reflections – When a point, a line segment, or a shape is reflected over a line it creates a mirror image.
3) Rotations – When we take a point, line, or shape and rotate it clockwise or counterclockwise, usually by 90º,180º, 270º, -90º, -180º, or -270º.
4) Dilations – When we take a point, line, or shape and make it bigger or smaller, depending on the Scale Factor.
Rigid Transformations:
Before we dive into our first type of transformation, let’s first define and explore what it means when a transformation maintains Rigid Motion. When a line or shape is transformed and the length, area and angles of the line and/or shape are unaffected by the transformation, it is considered to have Rigid Motion. Rigid transformations include Translations, Reflections, and Rotations (but not Dilations).
Now that we know which types of transformations mainatin rigid motion, let’s explore each type of transformation in more detail!
Translations:
Translations: When we take a shape, line, or point and we move it up, down, left, or right. Remember that this type of transformation is a rigid transformation, meaning the line or shape is translated, the length, area and angles of the line and/or shape are unaffected by the transformation.
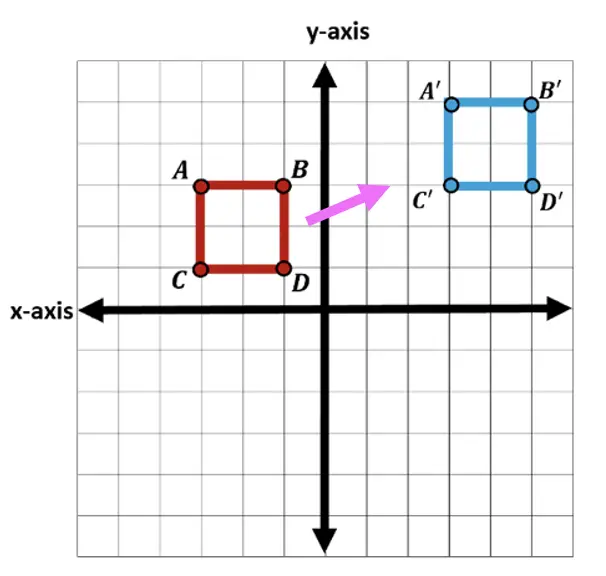
In the translation example above, we go start at square ABCD and translate each coordinate of the original square ABCD 6 units to the right and 2 units up to get our new transformed image square A|B|C|D| .
Translations Formula:
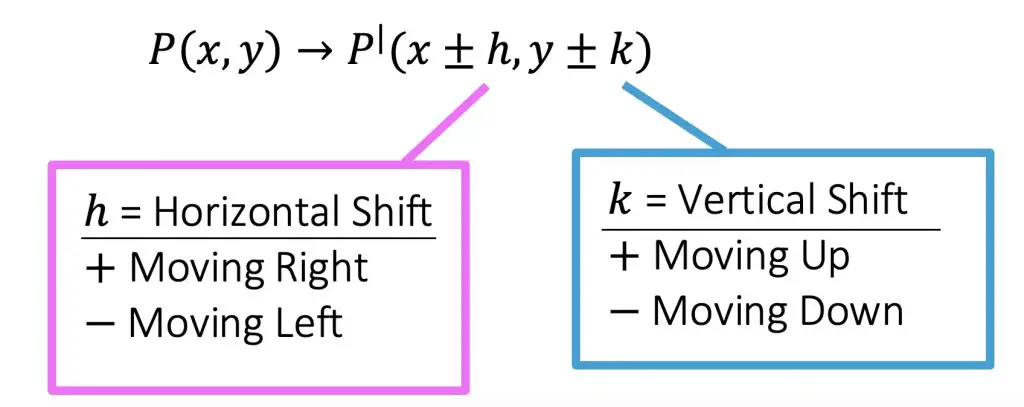
P(x,y) -> P| (x+h, y+k)
where….
h=Horizontal Shift (add (+) when moving right, subtract (-) when moving left)
k= Vertical Shift (add (+) when moving up, subtract (-) when moving down)
Horizontal Translation:
When we translate a point, line, or shape left or right, it is undergoing a horizontal translation along the x-axis. Any type of left or right movement on a coordinate plane is a horizontal translation.
How does this affect the x-coordinate? If the shape is being translated to the right, then we are adding units to the x-coordinate, and if the shape is shifting left then we are subtracting units from the x-coordinate.
Vertical Translation:
When we translate a point, line, or shape up or down, it is undergoing a vertical translation along the y-axis. Any type of up and down movement on a coordinate plane is a vertical translation.
How does this affect the y-coordinate? If the shape is being translated up, then we are adding units to the y-coordinate, and if the shape is being shifted down then we subtract from the y-coordinate.
Even though a horizontal shift or a vertical shift can happen when we move a shape, line, or point, many translations have a combo of the two!
How do Coordinates Change after a Translation?
The truth is there is no one unique rule for translations, but numbers will always be added or subtracted from the x and/or y coordinate values. If something is translated to the right, then we add units to the x-value. On the other had if something is translated to the left, we subtract units from the x-value. The same can be said for moving a shape up, we then add units to the y-value, and if a shape is translated down, we subtract units from the y-value. This gives us the following translation formula below:
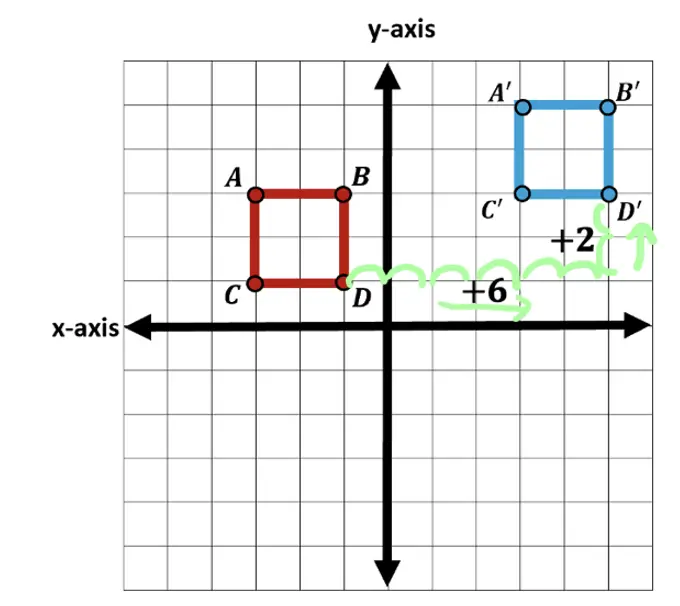
If we look at our example, when we translate original square ABCD to square A|B|C|D| we end up translating each coordinate of original square ABCD 6 units to the right and 2 units up. What we are really doing when we translate is adding 6 units to each x-coordinate as well as adding 2 units to each y-coordinate of the original figure square ABCD. Check it out below:
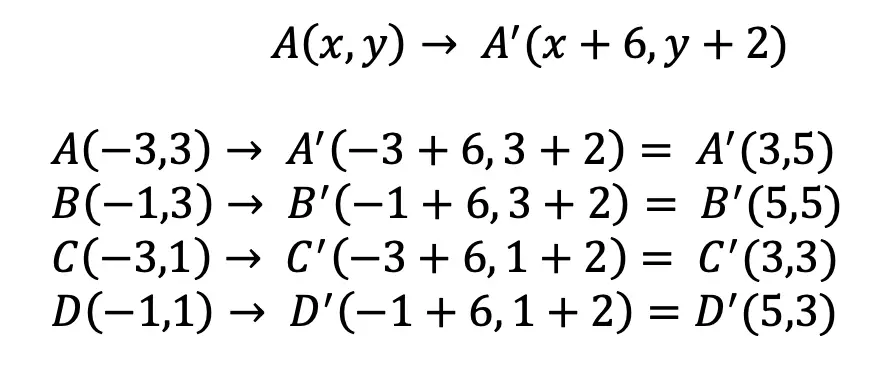
For more on translations, check out the video below and practice questions here.
Reflections:
Reflections on a coordinate plane are exactly what you think! When a point, a line segment, or a shape is reflected over a line it creates a mirror image. Think the wings of a butterfly, a page being folded in half, or anywhere else where there is perfect symmetry. Check out how we solve the reflections example below one step at a time!
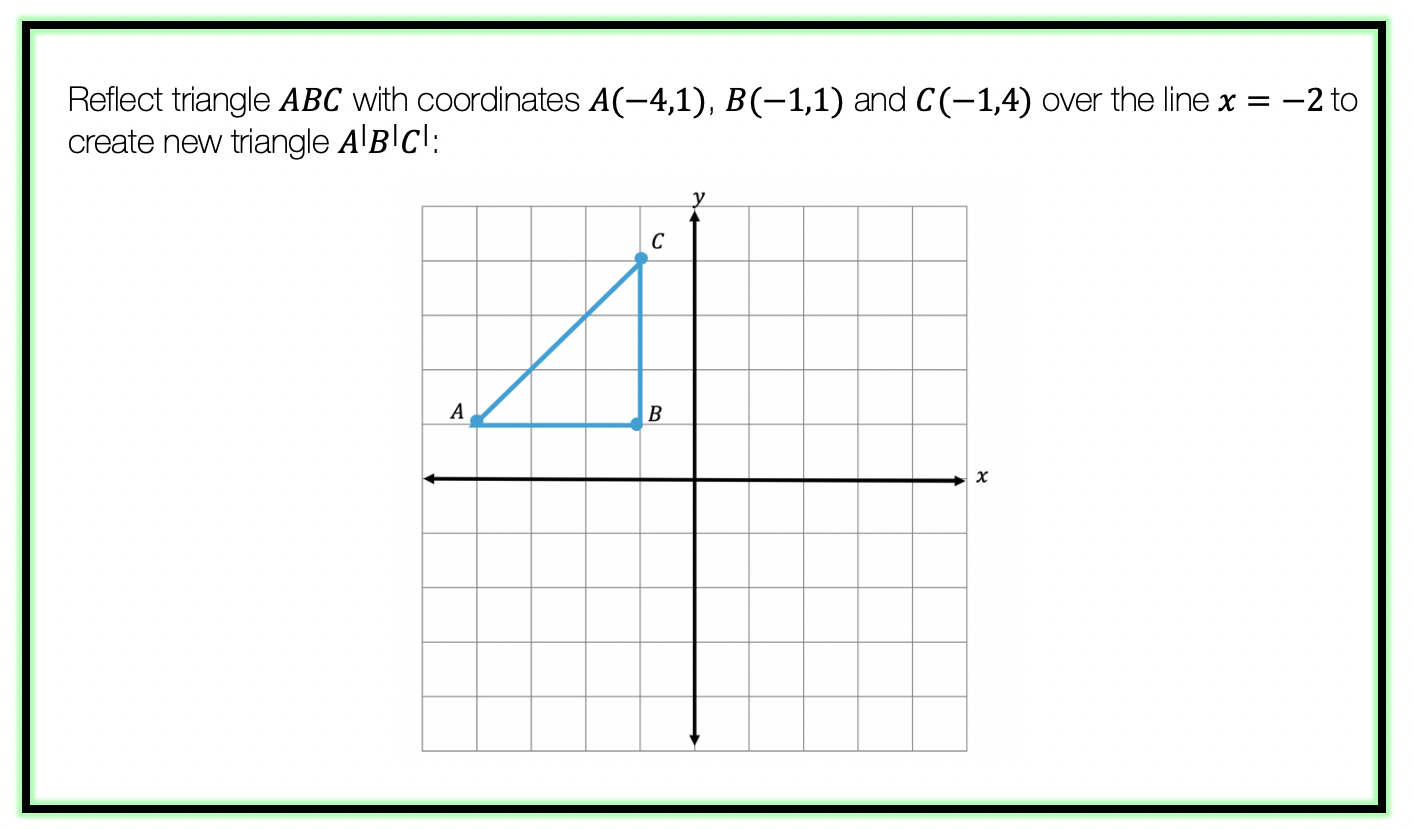
Step 1: First, let’s draw in line x=-2.
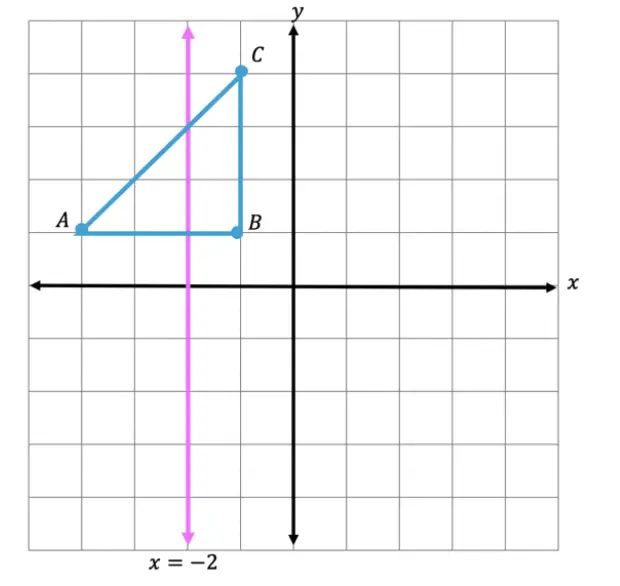
Step 2: Find the distance each point is from the line x=-2 and reflect it on the other side, measuring the same distance or mirror image of each point. First, let’s look at point C, notice it’s 1 unit away from the line x=-2, to reflect it we are going to count 1 unit (the same distance) to the left of the line x=-2 and label our new point, C|.
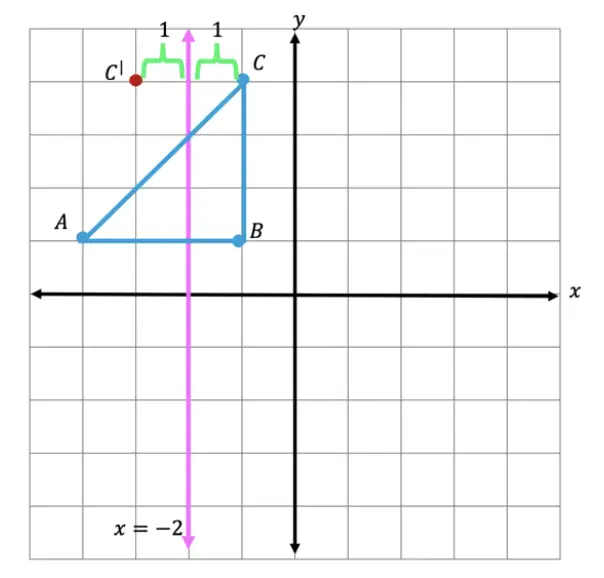
Step 3: Next we reflect point A in much the same way! Notice that point A is 2 units away on the left of line x=-2, we then measure 2 units to the right of our line and mark our new point, A|.
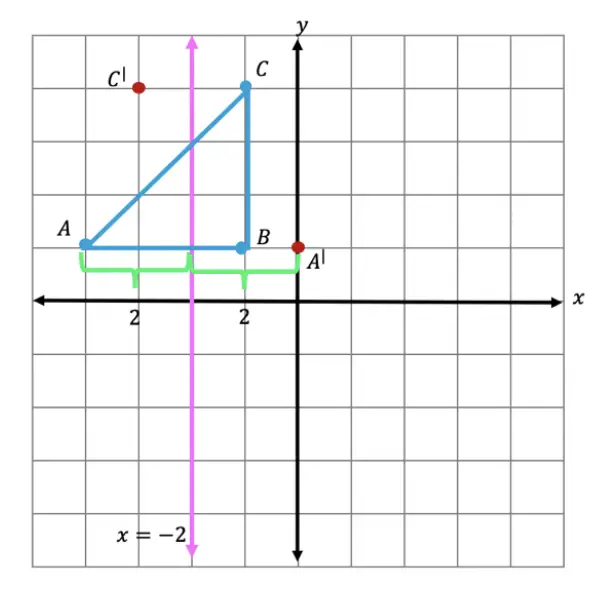
Step 4: Lastly, we reflect point B. This time, point B is 1 unit away on the right side of the line x=-2, we then measure 1 unit to the opposite side of our line and mark our new point, B|.
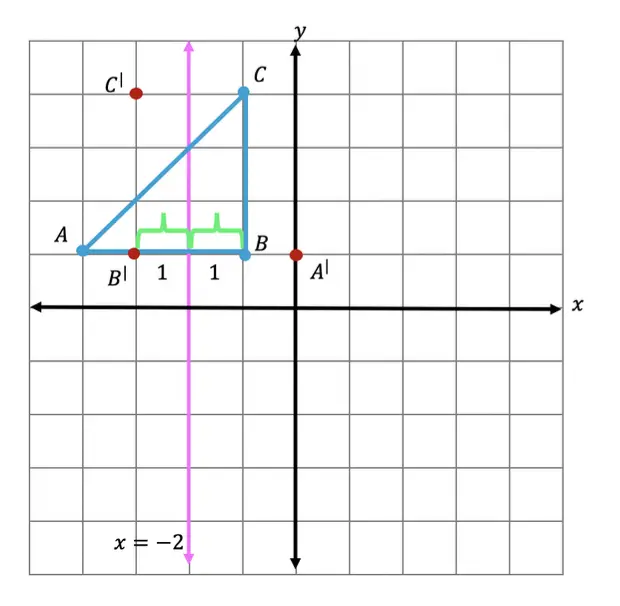
Step 5: Finally, we can now connect all of our new points, for our fully reflected triangle A|B|C|.
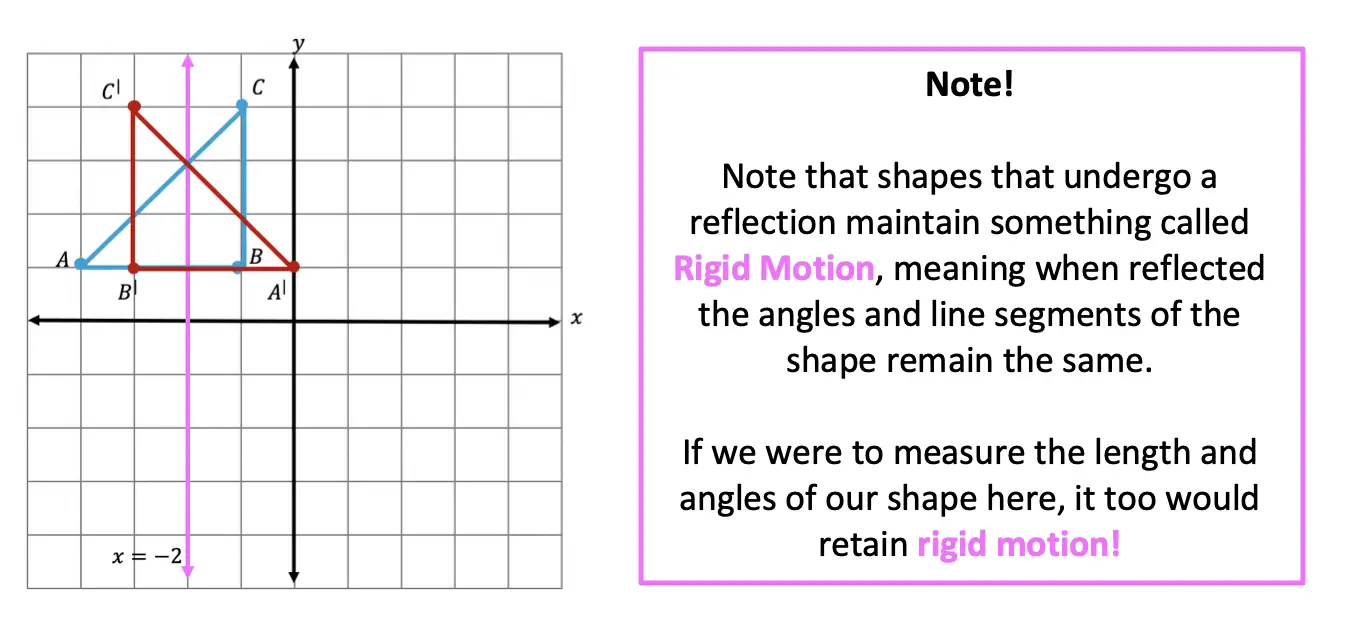
If you’re looking for more on reflections, check out the videos below and the practice questions right here.
Rotations:
Rotations are a type of transformation in geometry where we take a point, line, or shape and rotate it clockwise or counterclockwise, usually by 90º,180º, 270º, -90º, -180º, or -270º.
A positive degree rotation runs counter clockwise and a negative degree rotation runs clockwise. Let’s take a look at the difference in rotation types below and notice the different directions each rotation goes:
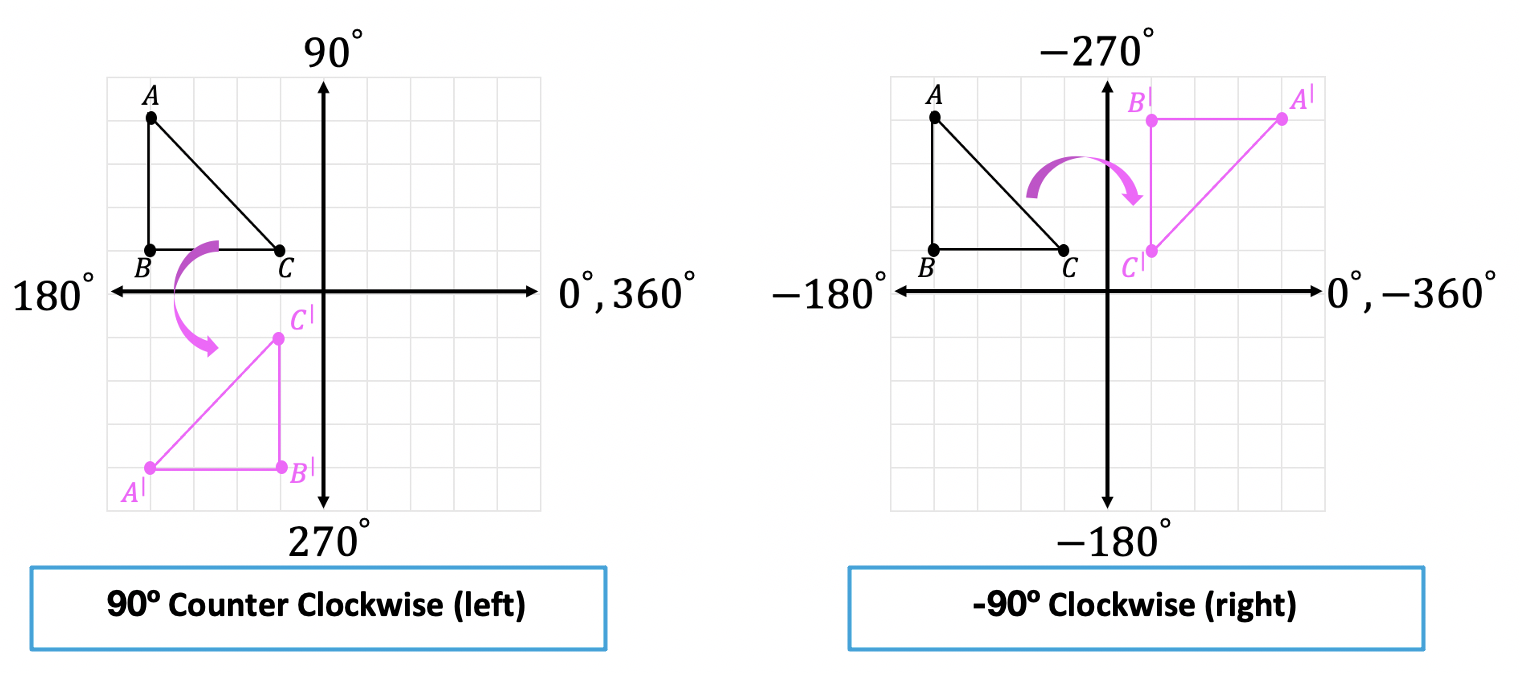
How do we rotate a shape?
There are a couple of ways to do this take a look at our choices below:
- We can visualize the rotation or use tracing paper to map it out and rotate by hand.
- Use a protractor and measure out the needed rotation.
- Know the rotation rules mapped out below. Yes, it’s memorizing but if you need more options check out numbers 1 and 2 above!
Rotation Rules:

Where did these rules come from?
To derive our rotation rules, we can take a look at our first example, when we rotated triangle ABC 90º counterclockwise about the origin. If we compare our coordinate point for triangle ABC before and after the rotation we can see a pattern, check it out below:
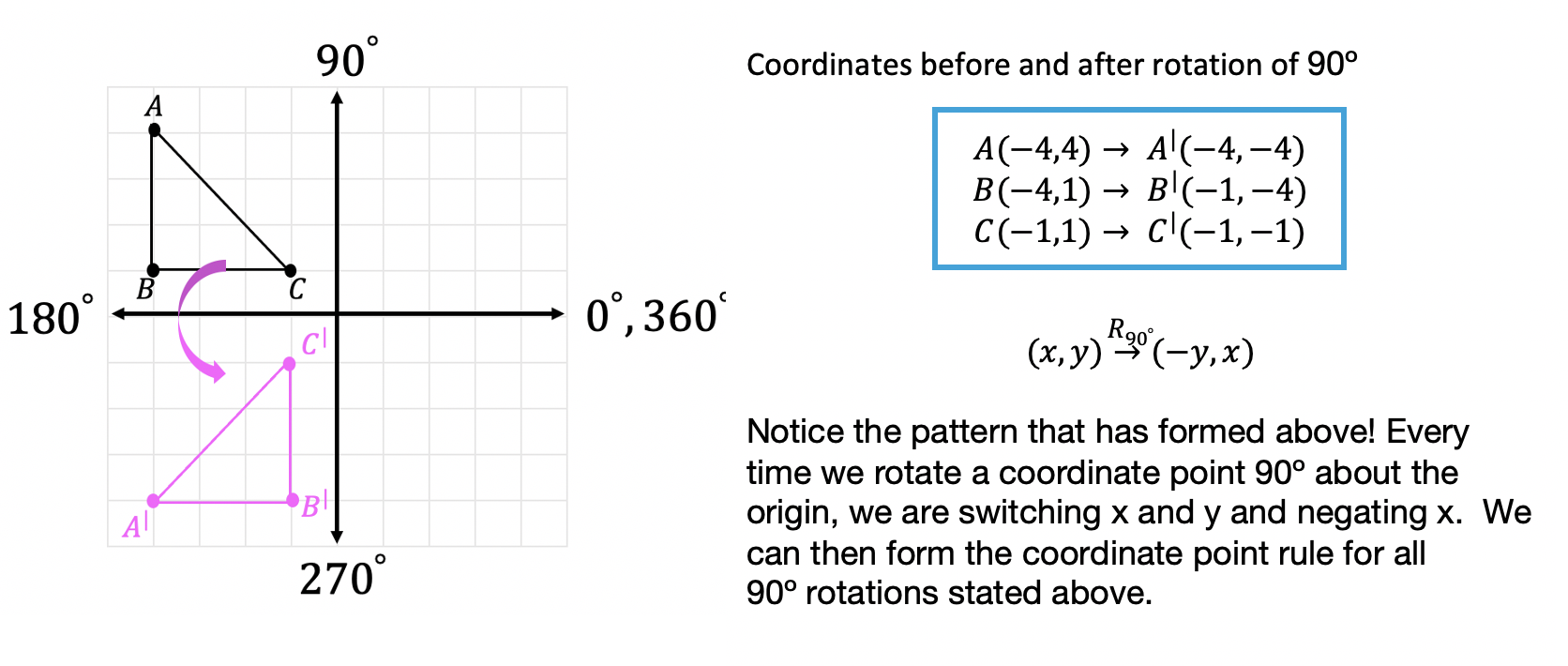
The rotation rules above only apply to those being rotated about the origin (the point (0,0)) on the coordinate plane. But points, lines, and shapes can be rotates by any point (not just the origin)! When that happens, we need to use our protractor and/or knowledge of rotations to help us find the answer. Let’s take a look at the Example below:
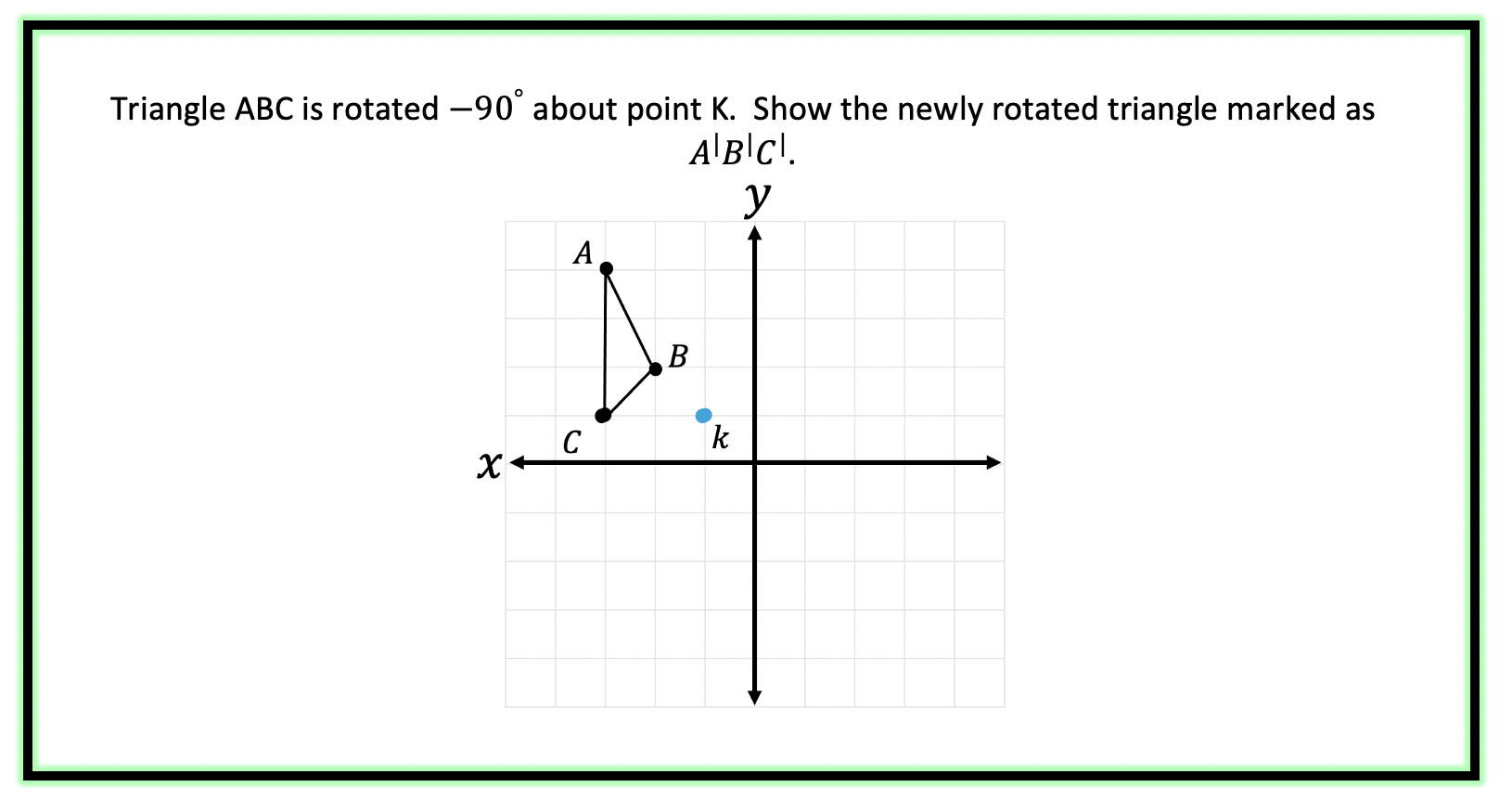
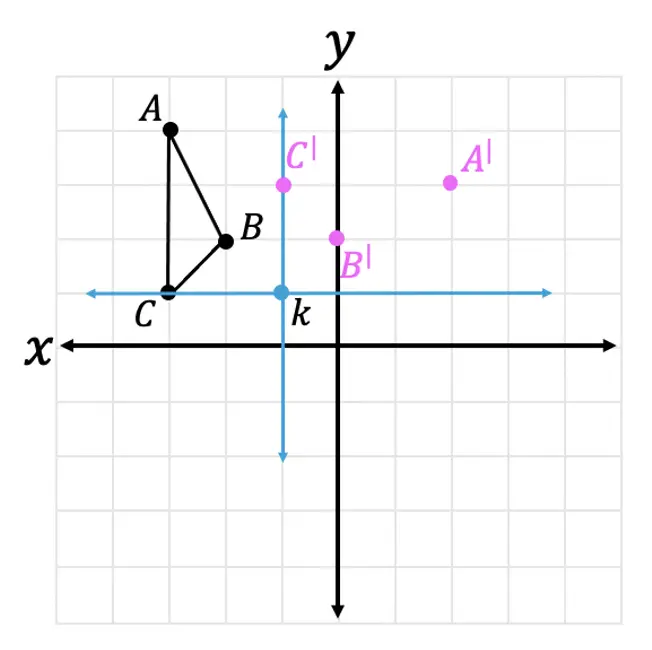
Step 1: First, let’s look at our point of rotation, notice it is not the origin we rotating about but point k! To understand where our triangle is in relation to point k, let’s draw an x and y axes starting at this point:
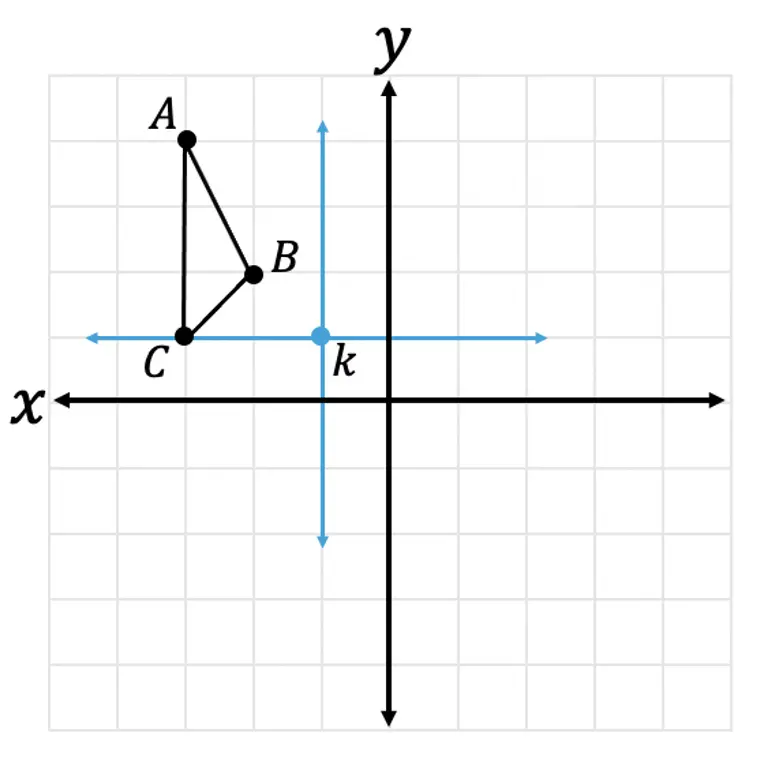
Step 2: Now let’s look at the coordinate point of our triangle, using our new axes that start at point k.
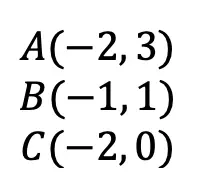
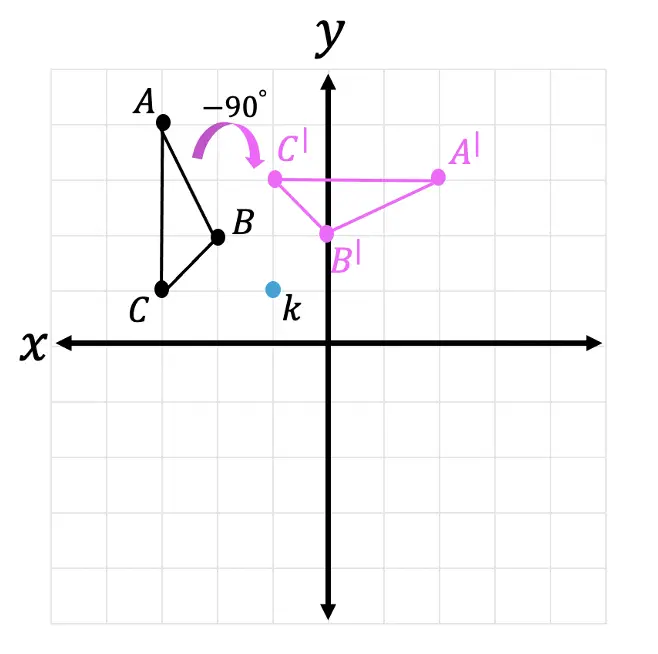
Step 2: Next, let’s take a look at our rule for rotating a coordinate -90º and apply it to our newly rotated triangles coordinates:
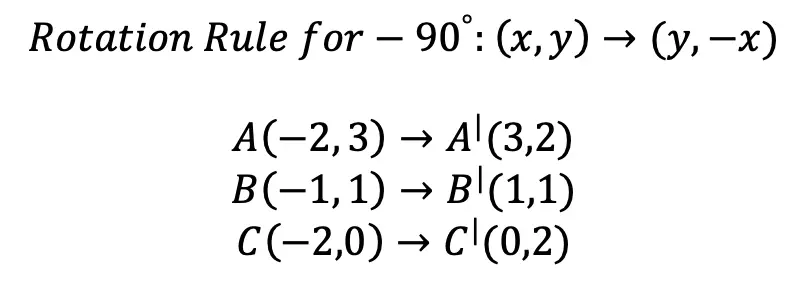
Step 3: Now let’s graph our newly found coordinate points for our new triangle .
Step 4: Finally let’s connect all our new coordinates to form our solution:
For more examples and practice questions, check out the video below and link here.
Dilations:
Dilations are a type of transformation in geometry where we take a point, line, or shape and make it bigger or smaller, depending on the Scale Factor.
We always multiply the value of the scale factor by the original shape’s length or coordinate point(s) to get the dilated image of the shape. A scale factor greater than one makes a shape bigger, and a scale factor less than one makes a shape smaller. Let’s take a look at how different values of scale factors affect the dilation below:
Scale Factor >1 Bigger
Scale Factor <1 Smaller
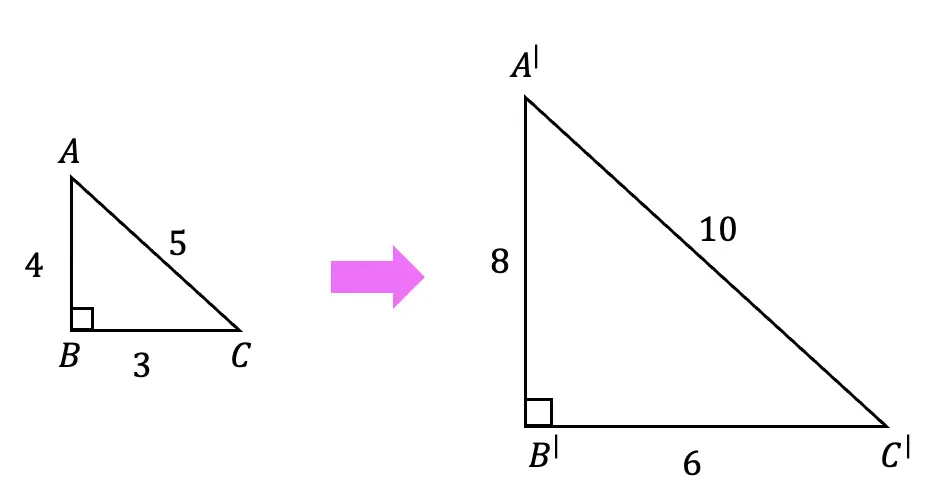
Scale Factor=2
In the below diagram the original triangle ABC gets dilated by a scale factor of 2. Notice that the triangle gets bigger, and that each length of the original triangle is multiplied by 2.
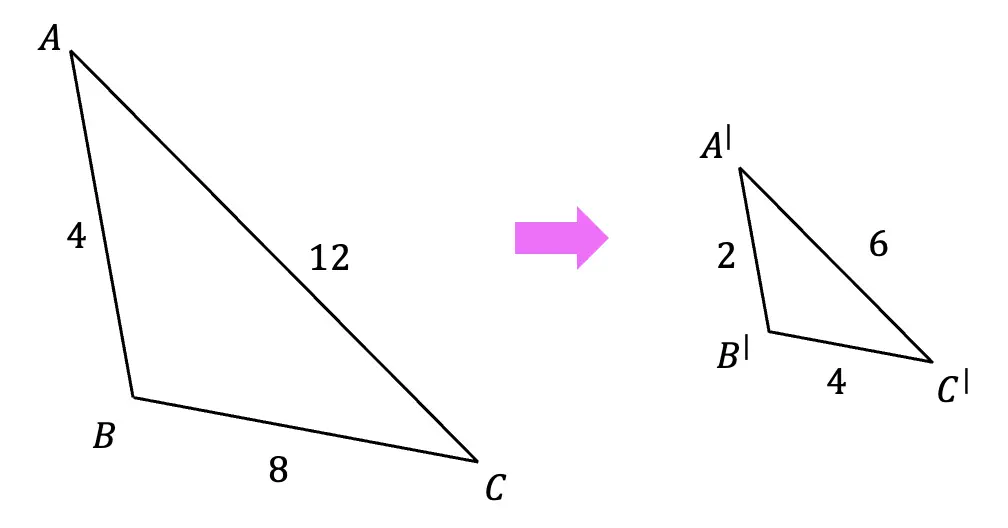
Scale Factor=1/2
Here, the original triangle ABC gets dilated by a scale factor of 1/2. Notice that the triangle gets smaller, and that each length of the original triangle is multiplied by 1/2 (or divided by 2).
Properties of Dilations:
There are few things that happen when a shape and/or line undergoes a dilation. Let’s take a look at each property of a dilation below:
1. Angle values remain the same.
2. Parallel and perpendicular lines remain the same.
3. Length, area, and perimeter do not remain the same.
*Notice Dilations are a non rigid transformation!
Now that we a bit more familiar with how dilations work, let’s look at some examples on the coordinate plane:
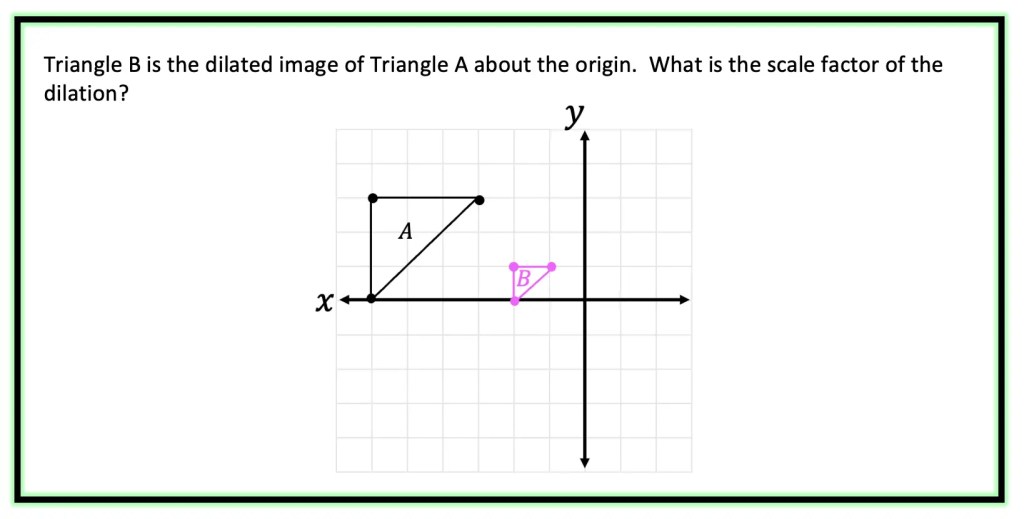
Step 1: First, let’s look at two corresponding sides of our triangle and measure their length.
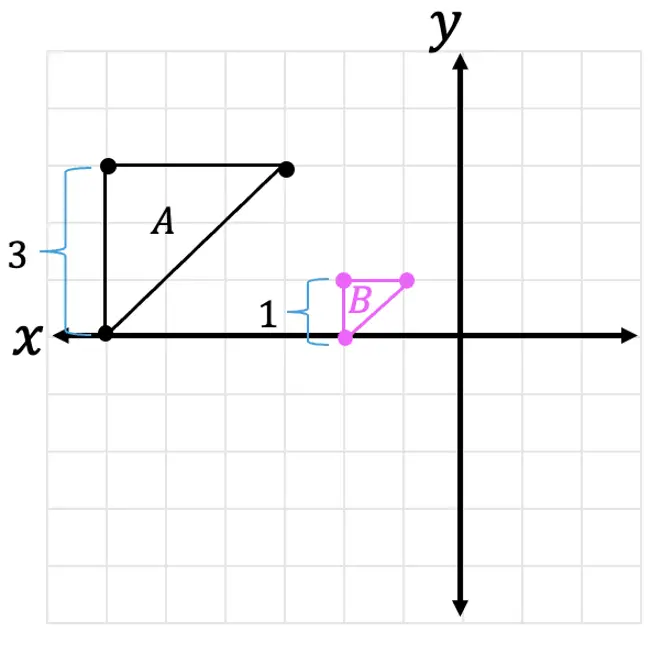
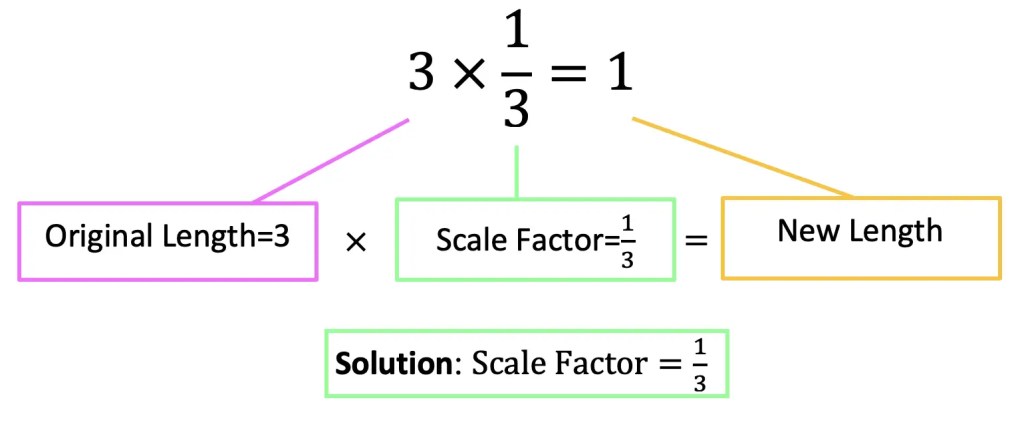
Step 2: Now, let’s look at the difference between the two lengths and ask ourselves, how did we go from 3 units to 1 unit?
Remember, we are always multiplying the scale factor by the original length values in order to dilate an image. Therefore, we know we must have multiplied the original length by 1/3 to get the new length of 1.
Dilating about a Point other than the Origin
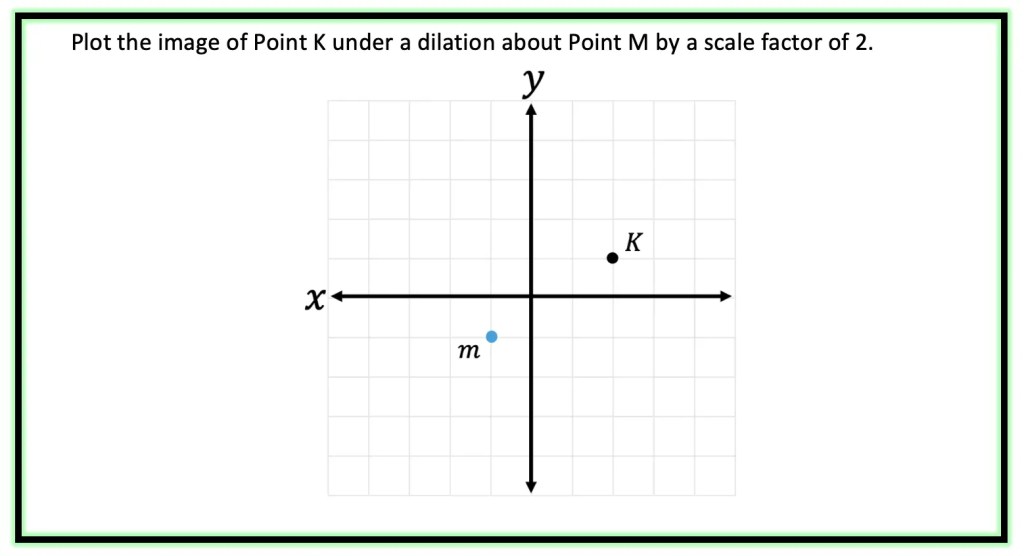
Step 1: First, let’s look at our point of dilation, notice it is not at the origin! In this question, we are dilating about point m! To understand where our triangle is in relation to point m, let’s draw a new x and y axes originating from this point in blue below.
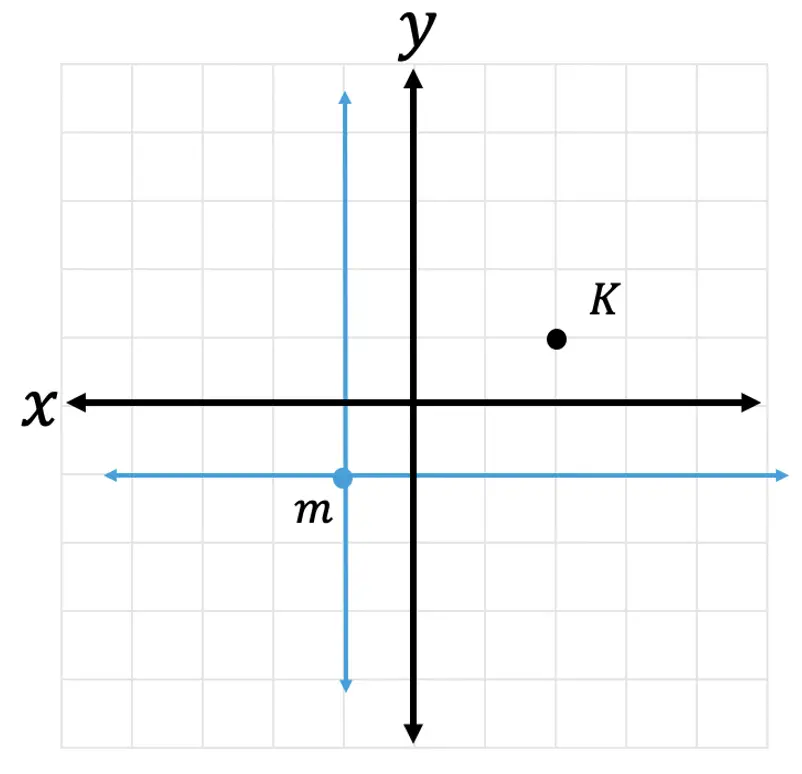
Step 2: Now, let’s look at coordinate point K, in relation to our new axes.
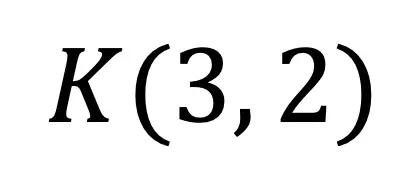
Step 3: Let’s use the scale factor of 2 and the transformation rule for dilation, to find the value of its new coordinate point. Remember, in order to perform a dilation, we multiply each coordinate point by the scale factor.
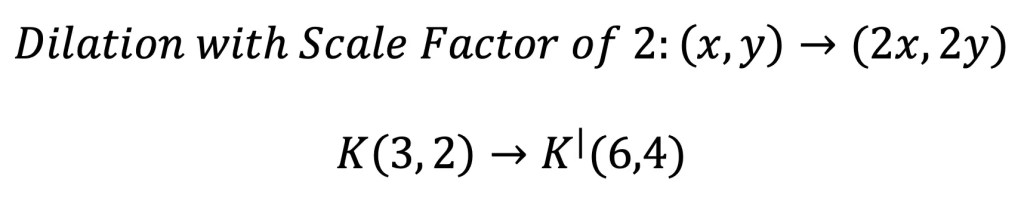
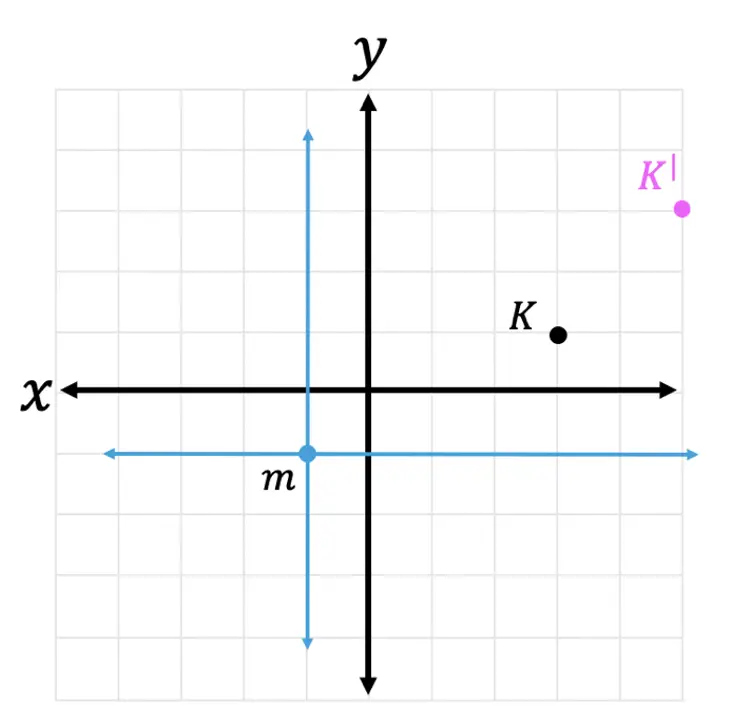
Step 4: Finally, let’s graph the dilated image of coordinate point K. Remember we are graphing the point (6,4) in relation to the x and y-axis that stems from point m.
If you’re looking for more on dilations, check out the video below and practice questions right here!
Transformations in the Real World?
If you think that you’ll never see real world use of transformations, think again! When playing the lovable game of Tetris, we are rotating shapes to clear lines, transforming each shape as we go.
Besides playing Tetris, Transformations in math can be found within the game itself, within its code. Game developers will need to be familiar with coordinate rules for how to flip and rotate a shape within their code for Tetris or any other game out there!
You can also think of real-life objects to transform (as opposed to just the digital ones mentioned above). This can be anything from parking a car to building a house, to landing an airplane. Can you think of transformations you use in your everyday life? Let us know in the comments!
Still got questions about math transformations? No problem! Don’t hesitate to comment with any questions below. Want more math transformations? Don’t forget to check out the videos and practice questions for each linked throughout this article. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube


