Hi there and welcome to MathSux! Today we are going to break down dilations; what they are, how to find the scale factor, and how to dilate about a point other than the origin. Dilations are a type of transformation that are a bit different when compared to other types of transformations out there (translations, rotations, reflections). Once a shape is dilated, the length, area, and perimeter of the shape change, keep on reading to see how! And if you’re looking for more transformations, check out these posts on reflections and rotations. Thanks so much for stopping by and happy calculating! 🙂
What are Dilations?
Dilations are a type of transformation in geometry where we take a point, line, or shape and make it bigger or smaller, depending on the Scale Factor.
We always multiply the value of the scale factor by the original shape’s length or coordinate point(s) to get the dilated image of the shape. A scale factor greater than one makes a shape bigger, and a scale factor less than one makes a shape smaller. Let’s take a look at how different values of scale factors affect the dilation below:
Scale Factor >1 Bigger
Scale Factor <1 Smaller
Scale Factor=2
In the below diagram the original triangle ABC gets dilated by a scale factor of 2. Notice that the triangle gets bigger, and that each length of the original triangle is multiplied by 2.
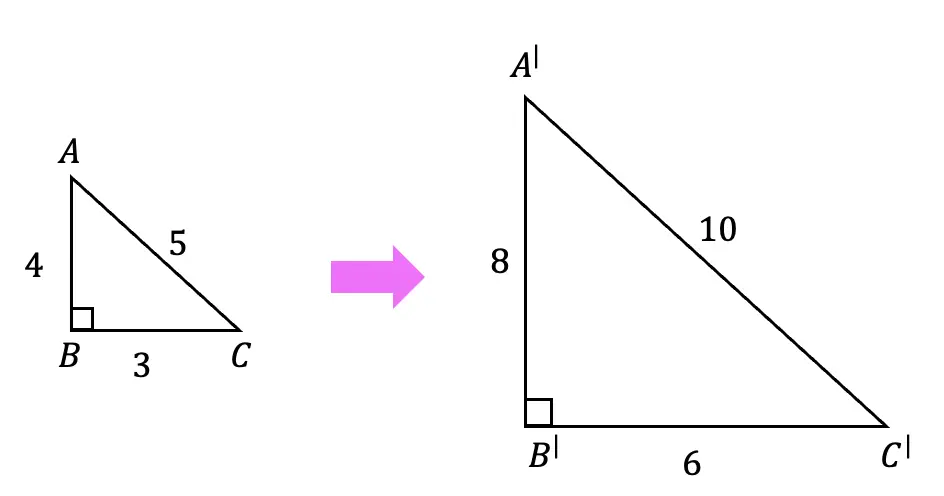
Scale Factor=1/2
Here, the original triangle ABC gets dilated by a scale factor of 1/2. Notice that the triangle gets smaller, and that each length of the original triangle is multiplied by 1/2 (or divided by 2).
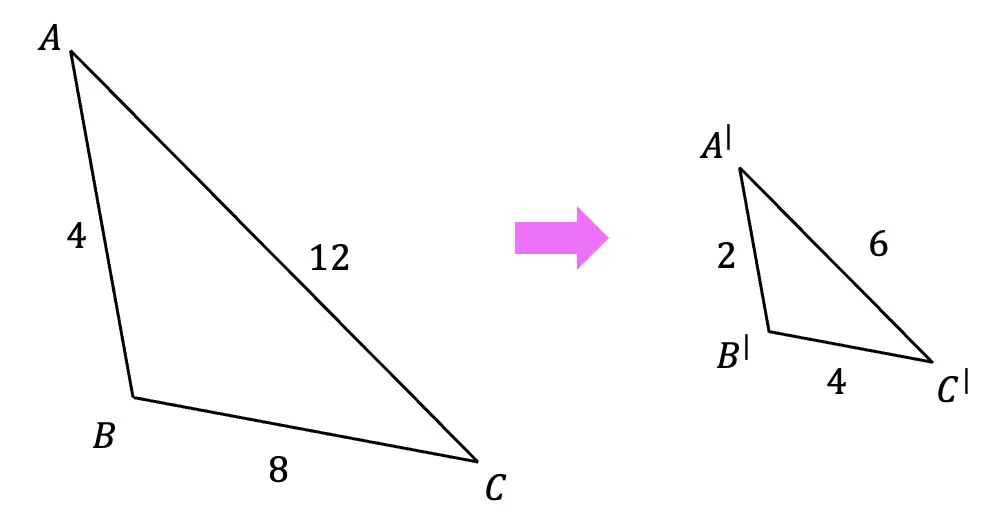
Properties of Dilations:
There are few things that happen when a shape and/or line undergoes a dilation. Let’s take a look at each property of a dilation below:
1. Angle values remain the same.
2. Parallel and perpendicular lines remain the same.
3. Length, area, and perimeter do not remain the same.
Now that we a bit more familiar with how dilations work, let’s look at some examples on the coordinate plane:
Example #1: Finding the Scale Factor
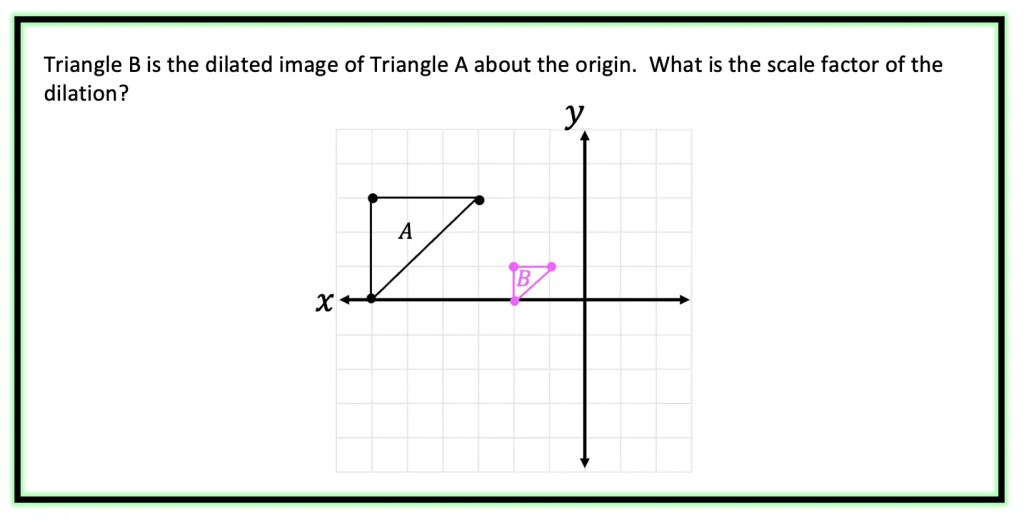
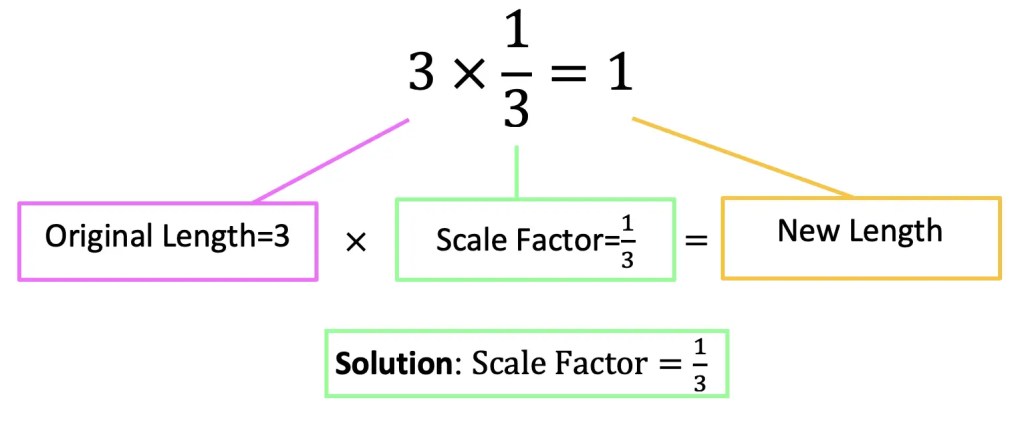
Step 1: First, let’s look at two corresponding sides of our triangle and measure their length.
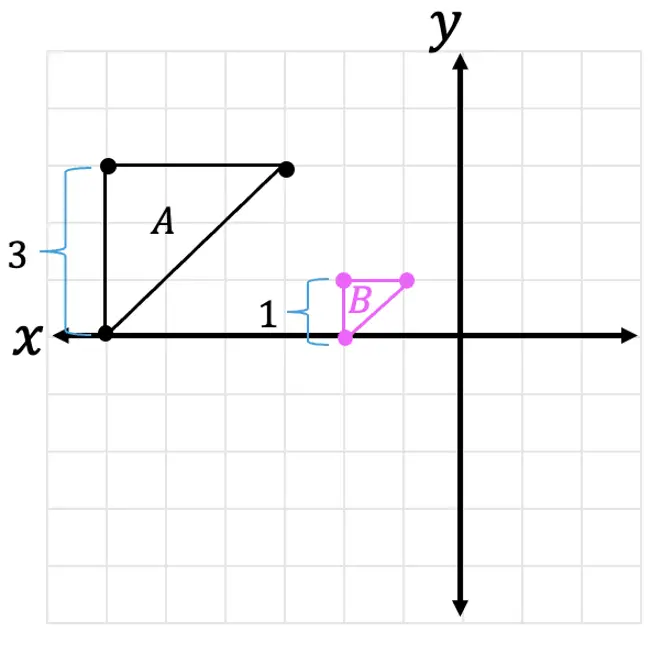
Step 2: Now, let’s look at the difference between the two lengths and ask ourselves, how did we go from 3 units to 1 unit?
Remember, we are always multiplying the scale factor by the original length values in order to dilate an image. Therefore, we know we must have multiplied the original length by 1/3 to get the new length of 1.
When it comes to dilations, there are different types of questions we may be faced with. In the last question, the triangle dilated was done so about the origin, but this won’t always be the case. Let’s see how to dilate a point about a point other than the origin with this next example.
Example #2: Dilating about a Point other than the Origin
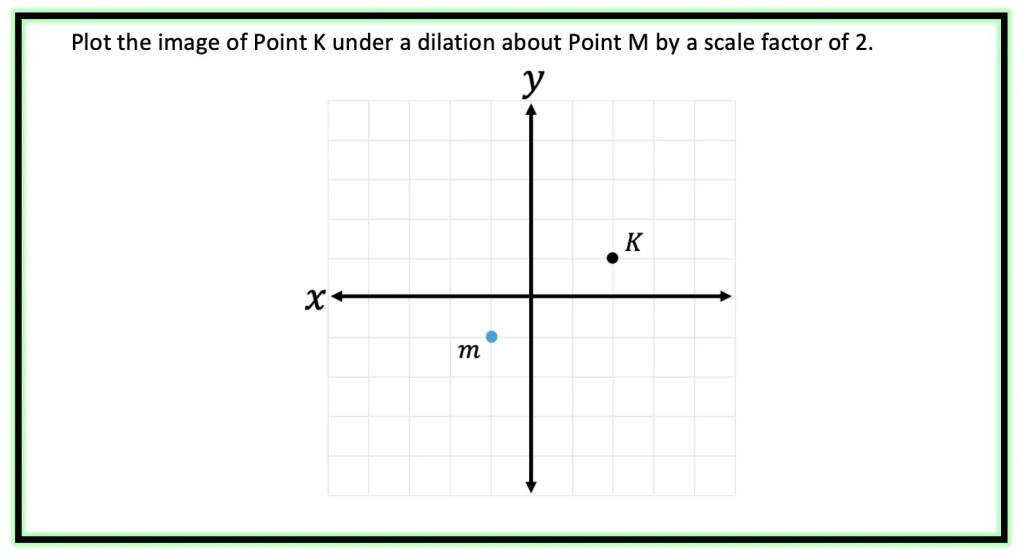
Step 1: First, let’s look at our point of dilation, notice it is not at the origin! In this question, we are dilating about point m! To understand where our triangle is in relation to point m, let’s draw a new x and y axes originating from this point in blue below.
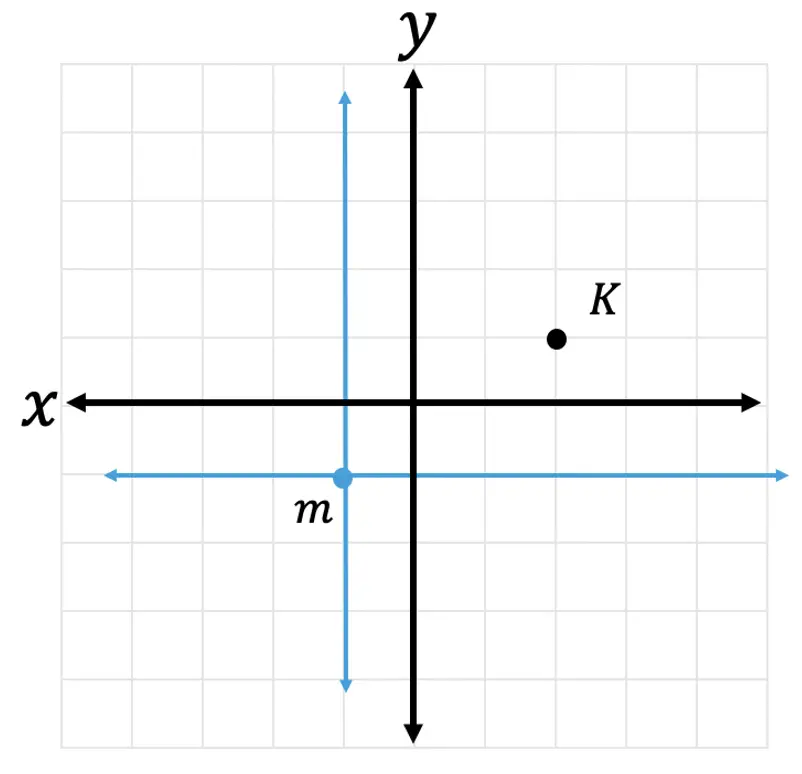
Step 2: Now, let’s look at coordinate point K, in relation to our new axes.
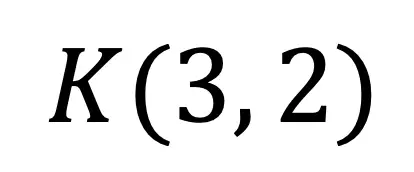
Step 3: Let’s use the scale factor of 2 and the transformation rule for dilation, to find the value of its new coordinate point. Remember, in order to perform a dilation, we multiply each coordinate point by the scale factor.
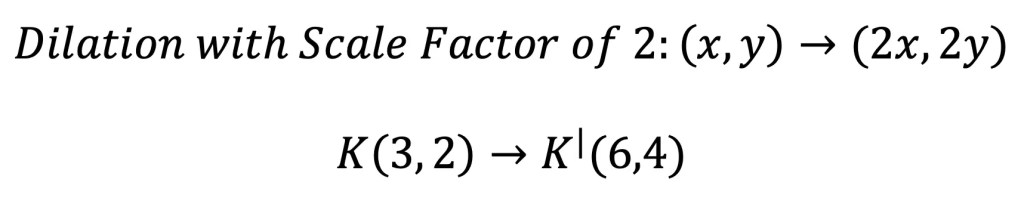
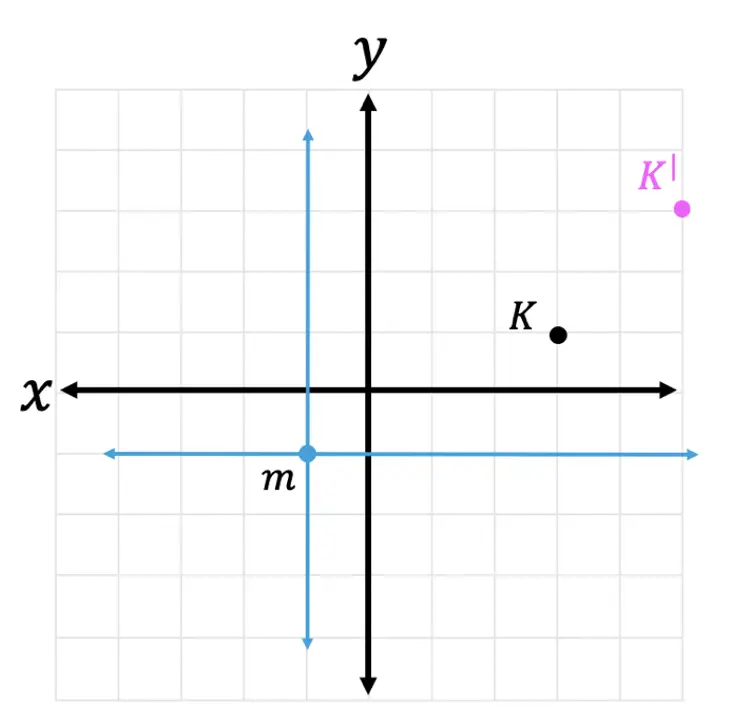
Step 4: Finally, let’s graph the dilated image of coordinate point K. Remember we are graphing the point (6,4) in relation to the x and y-axis that stems from point m.
Check out these dilation questions below!
Practice Questions:
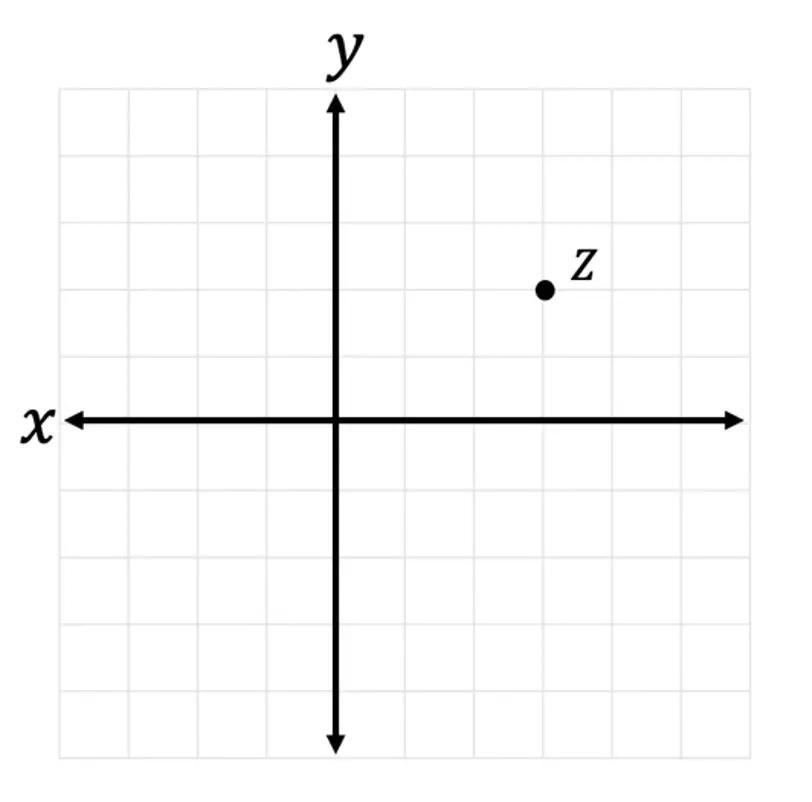
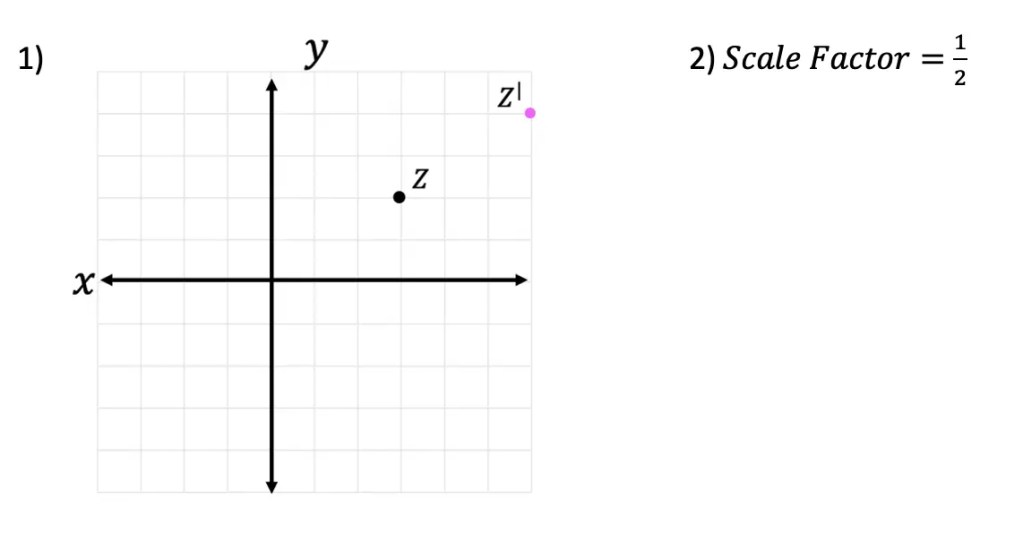
1) Plot the image of Point Z under a dilation about the origin by a scale factor of 2.
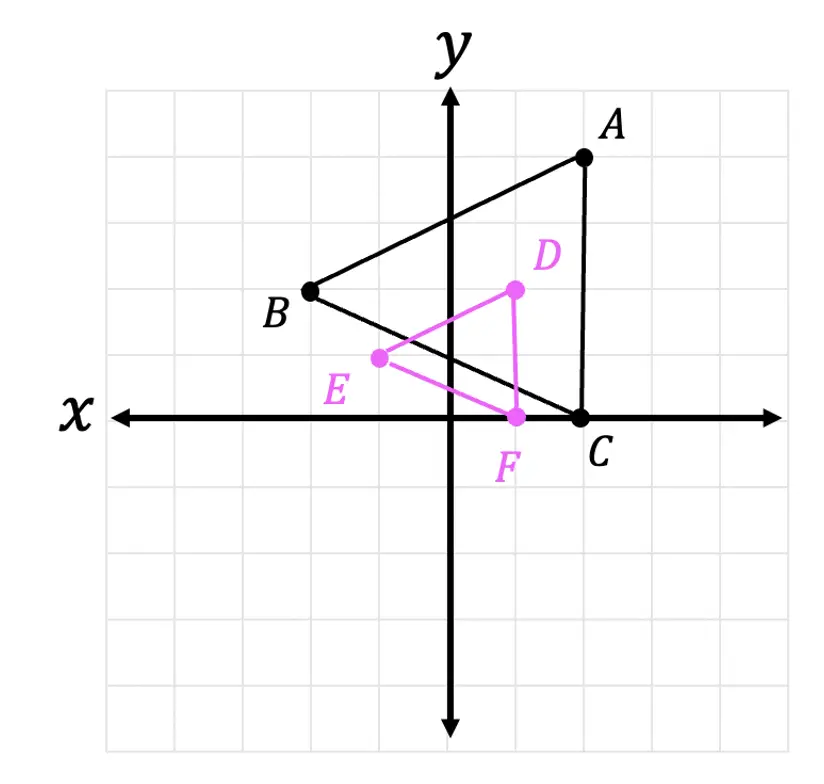
2) Triangle DEF is the image of triangle ABC after a dilation about the origin. What is the scale factor of the dilation?
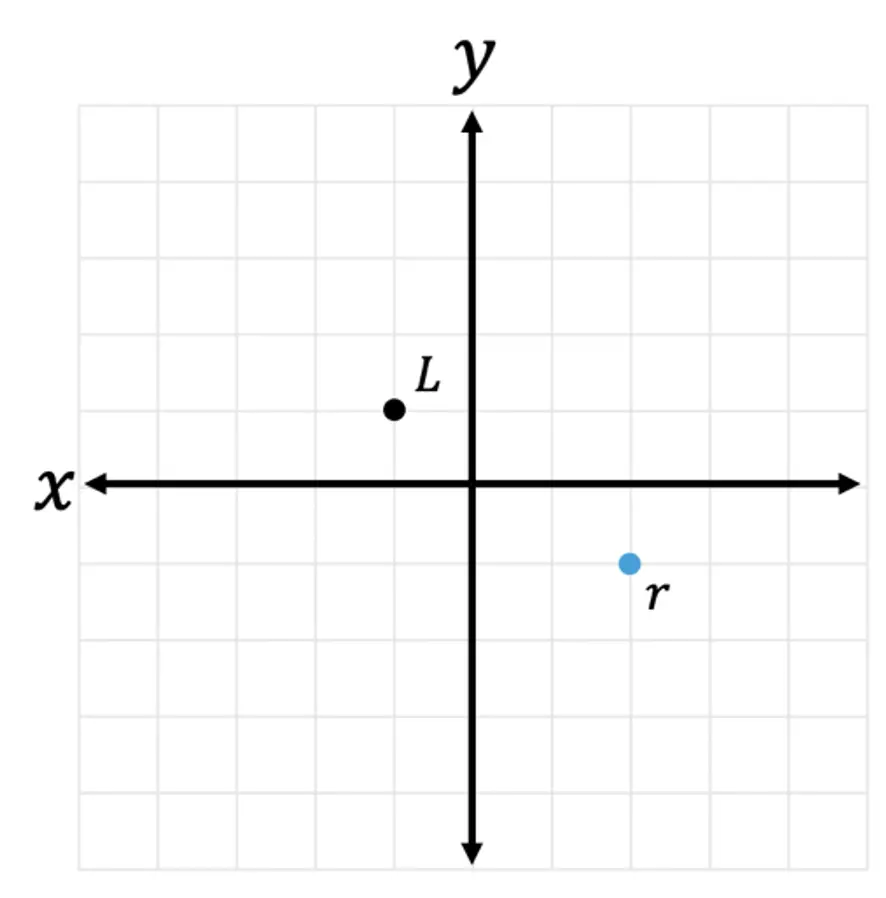
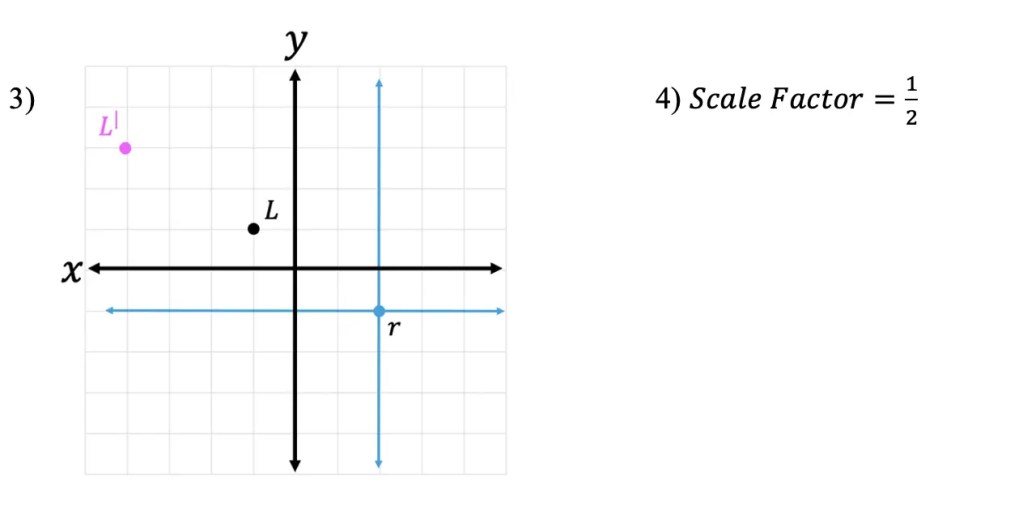
3) Point L is dilated by a scale factor of 2 about point r. Draw the dilated image of point L.
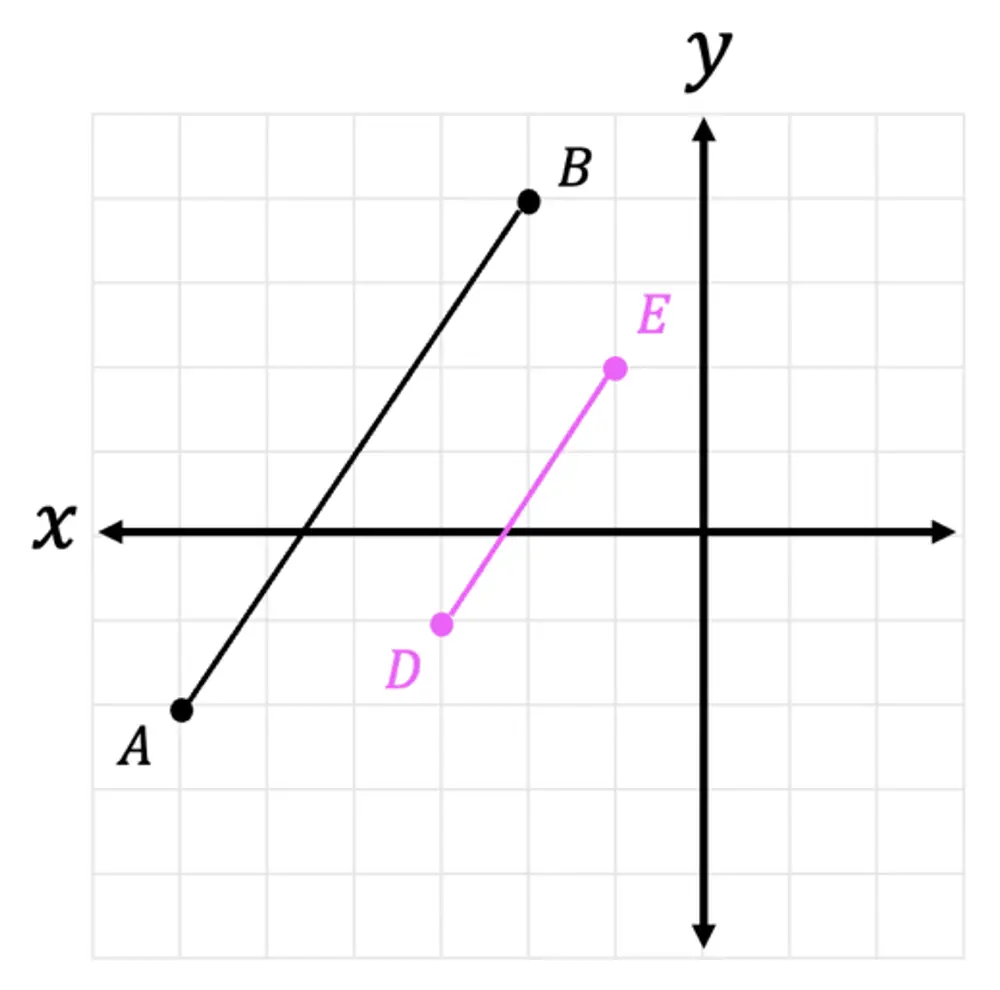
4) Line DE is the dilated image of line AB. What is the scale factor of the dilation?
Solutions:
Still got questions? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Looking for more Transformations? Check out the related posts below!

2 thoughts on “Dilations: Scale Factor & Points Other than Origin”