Greetings and welcome to MathSux! In today’s post we are going to go over everything you need to know about circles. We will start by going over the different parts of a circle including the centre of the circle, radius, chord, tangent, and secant. Then we will break down different formulas of a circle to know which include area, circumference, area of a sector, and several different circle theorems used to find missing angles and arcs.
Below is a cheat sheet that sums everything up in this post, but if you keep reading, we’ll get into more detail about how these theorems work with different examples and explanations. So keep scrolling, keep reading, stay positive, and happy calculating!
Free Downloadable Circle Theorem Cheat Sheet:
Parts of a Circle:
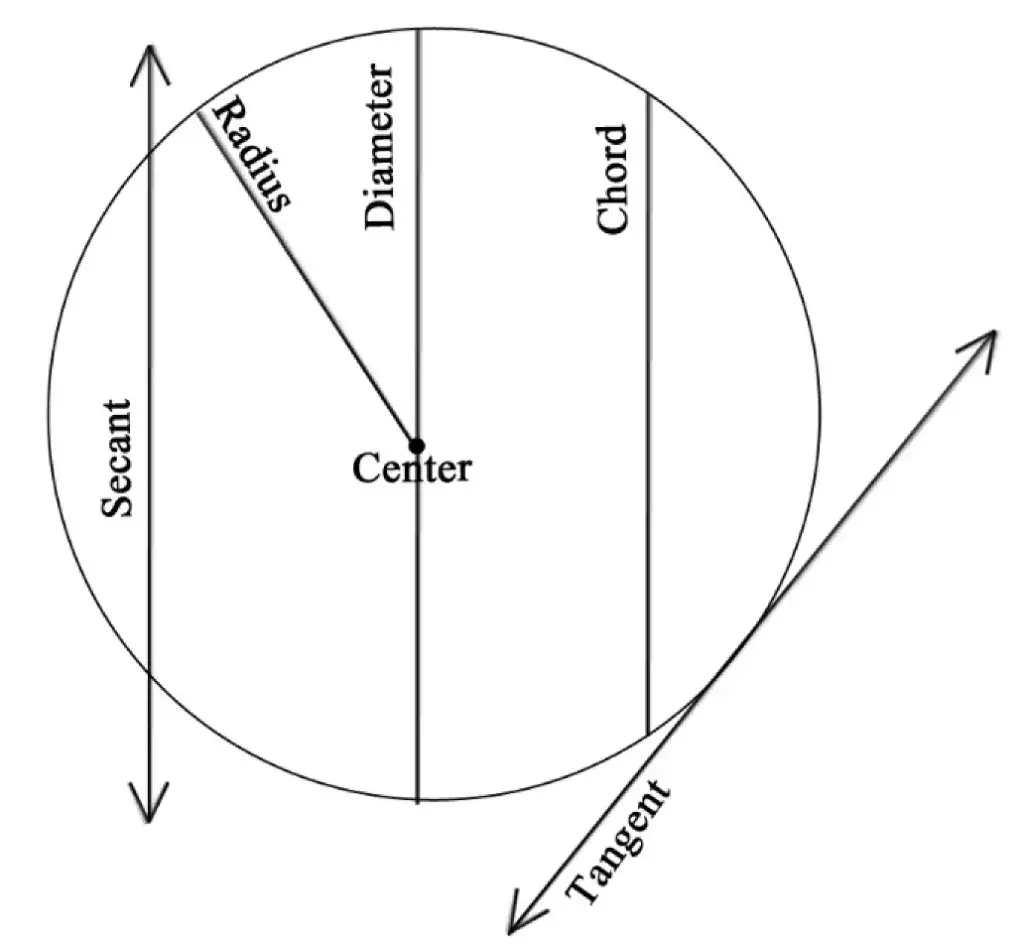
There are so many different parts to a circle! Let’s take a closer look at each part below with the following definitions:
- Diameter: A line that cuts a circle in half through its center.
- Radius: A line that goes from the center point to the edge of the circle. (Otherwise known as half the length of the diameter).
- Center: All points along the circle are equidistant from this point.
- Chord: A line segment that has endpoints along a circle but does not cross its center.
- Tangent: A continuous line that only touches the outer part of the circle.
- Secant: A line that cuts through a circle at two points.
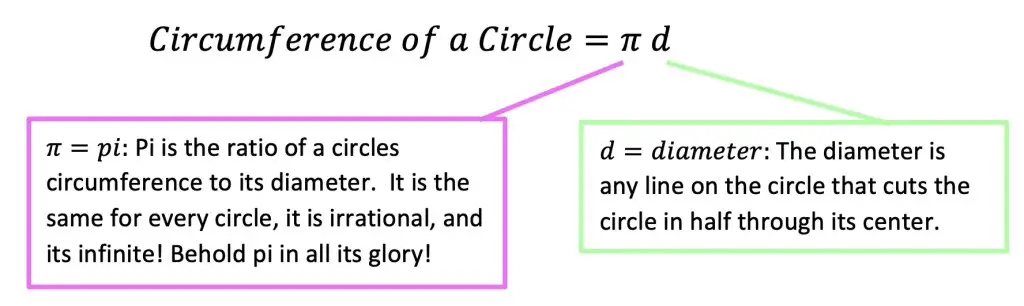
Circle’s Circumference:
A circle’s Circumference, measures the distance of length around the entire circle. It is like we are taking a walk around the circle and measuring how far we go along the way until we’re back where we started.
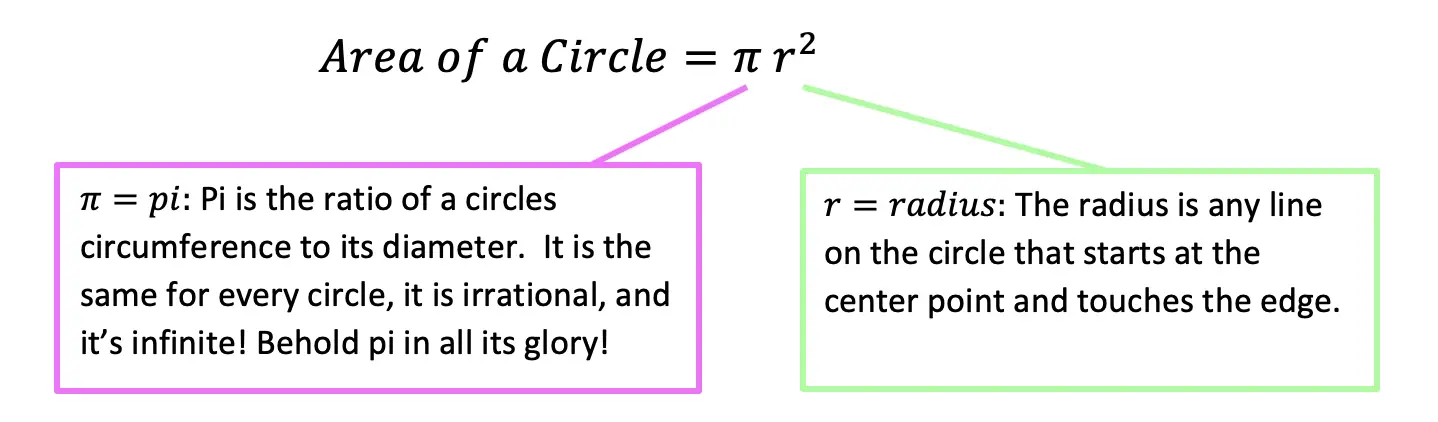
Area of a Circle:
The Area of a circle allows us to find the “area” or total value found within outline of a circle.
Area of a Sector:
We already know how to find the area of a circle, but what about the area of a sector? What does a sector even mean? A Sector is a piece of a circle, kind of like a piece of pie. Check out the example here for a clearer picture.
Arcs, Angles, & Measures of a Circle:
The Arc of a circle is a piece of the circle’s circumference. Think of an arc like the outline of a piece of the pie, yum!
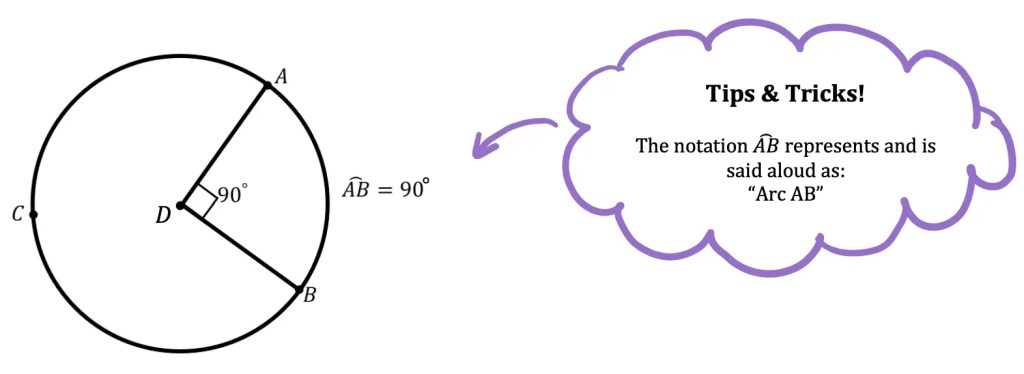
What’s with the degrees and arc AB notation ? Is there a difference?
An arc is measured in degrees by its central angle value (called an arc’s measure). An arc is also measured by length in units of measurement such as inches or centimeters. Let’s look at the difference between each below:
Measure: The measure of an arc is the degree size of its central angle. In the example below, we can see that the degree value of arc AB is 90º (hi-lighted in green)
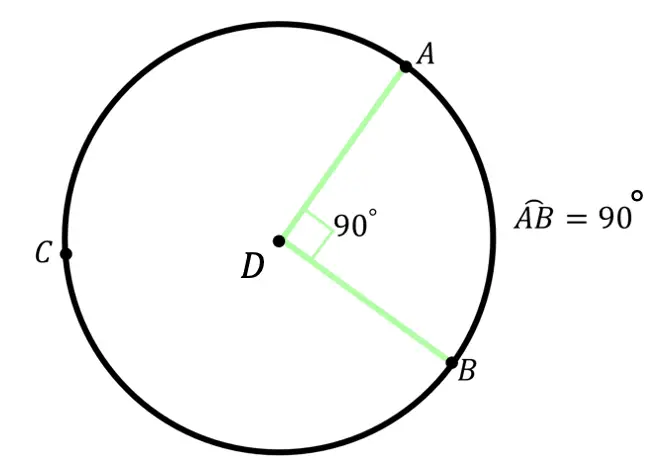
Length: The length of an arc is the length of the circle’s circumference and can be measured in units such as feet, inches, centimeters, etc. (hi-lighted in pink)
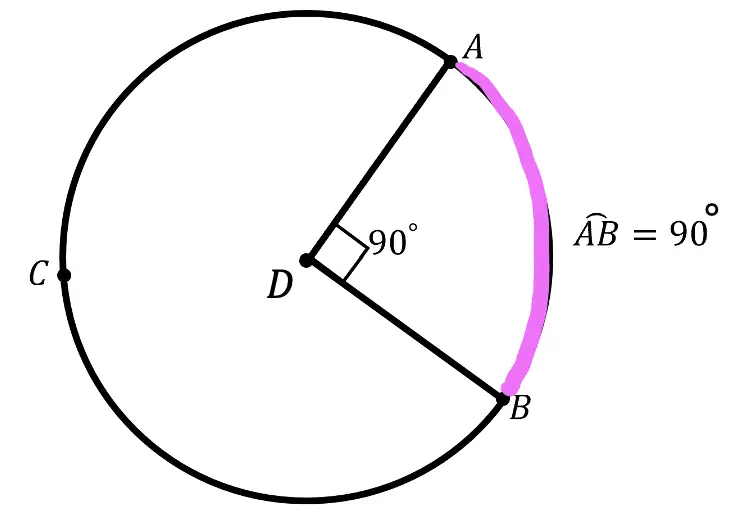
Are there different types of arcs?
There are two main different types of arcs: a major arc and a minor arc. As you may guess, one is bigger and one is smaller. Let’s look at an Example:
Major Arc: An arc with a measure value greater than 180º (greater than half the circle). In the Example below, we can see that the major arc can be represented by arc AB (hi-lighted in green).
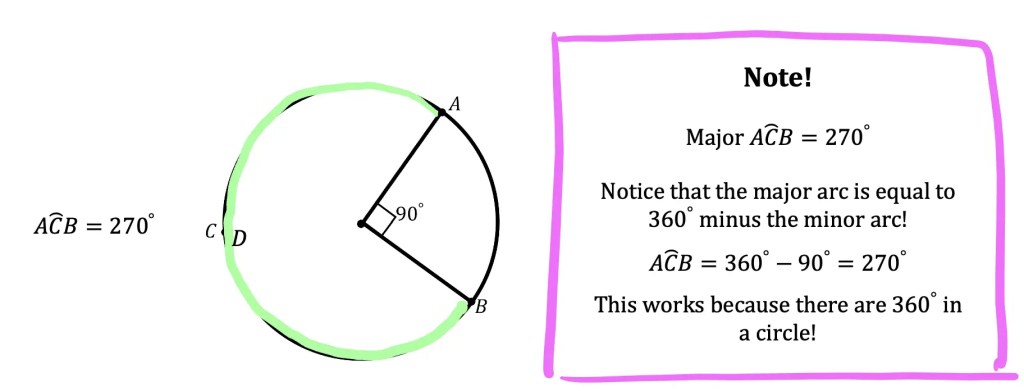
Minor Arc: An arc with a measure value less than 180º (less than half the circle). In the Example below, we can see that the minor arc can be represented by arc AB (hi-lighted in pink).
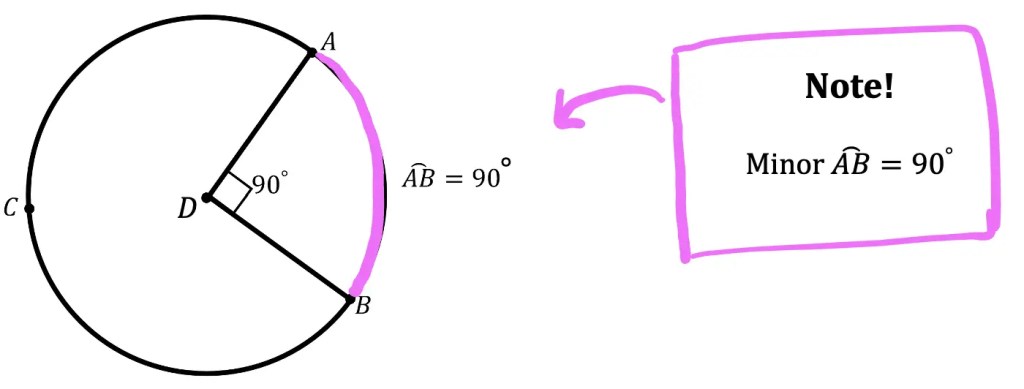

How do we calculate an arcs Length and Measure?
Finding Arc Length: To find the length of an arc, we only need one formula!

Finding Arc Measure: Calculating an arc’s measure varies depending on the presence of secants, tangents, chords, and radii. In fact, there are seven different potential situations for finding arcs measure! Surprising, I know, but let’s look at each type one at a time:
- Central Angle (Two radii): When two radii are drawn from the center point of a circle, they form a central angle. A central angle is equal to the length of the arc. In the Example below, we see that arc AB has a length of 90º and has an arc measure of 90º. They are equal!

For more on central angles, check out the post here for practice questions and the video below:
2. Inscribed Angle: When two chords come together to touch the outline of a circle, they create something called an inscribed angle. An inscribed angle is equal to half the value of the arc length.

For more on inscribed angles, check out the post and practice questions here, and video below!
3. Intersecting Chords: When two chords intersect, they create four arcs and two sets of vertical angles. Each set of vertical angles is congruent. To find the value of one vertical angle, add the two arc lengths together and divide by 2.
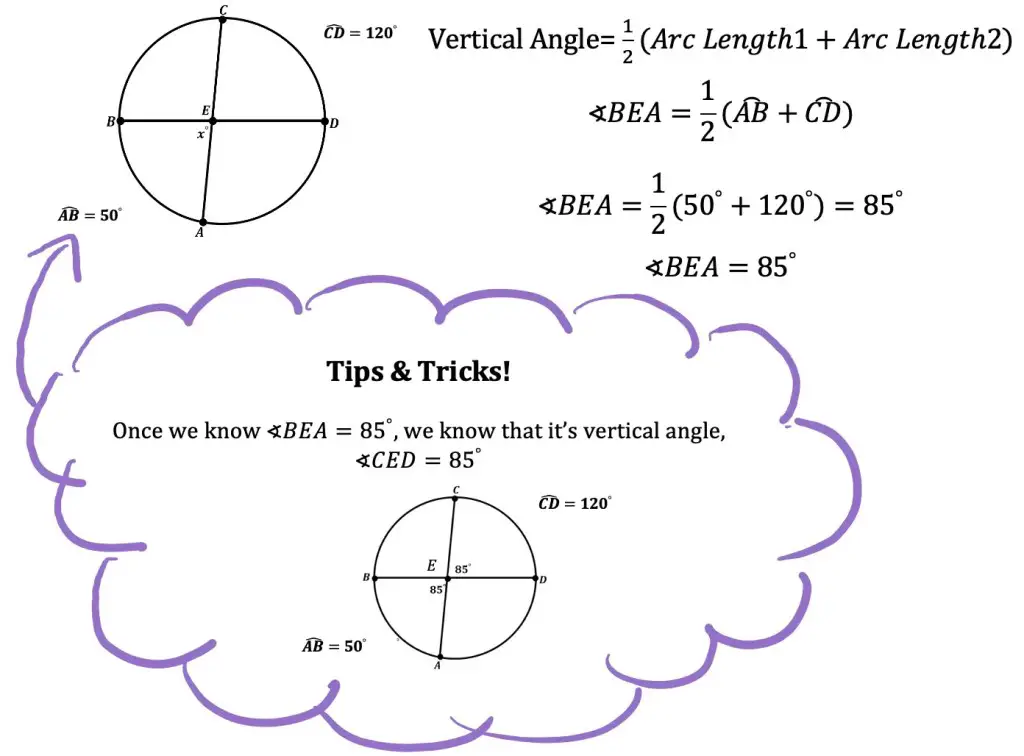
4. Tangent and Chord: When a tangent and chord connect, they create an angle that touches the outline of the circle. The angle formed is equal to half the arc length.
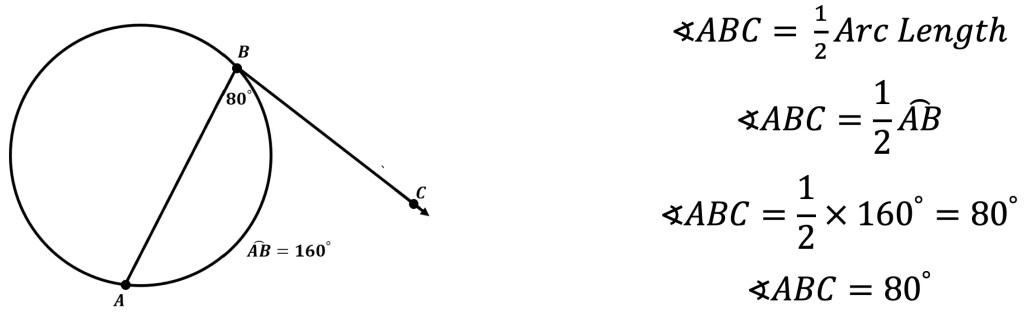
5. Two Tangents: When two tangents touch the outer edge of the circle, it creates an angle. The angle is equal to the difference between the intercepted arc lengths divided by two.
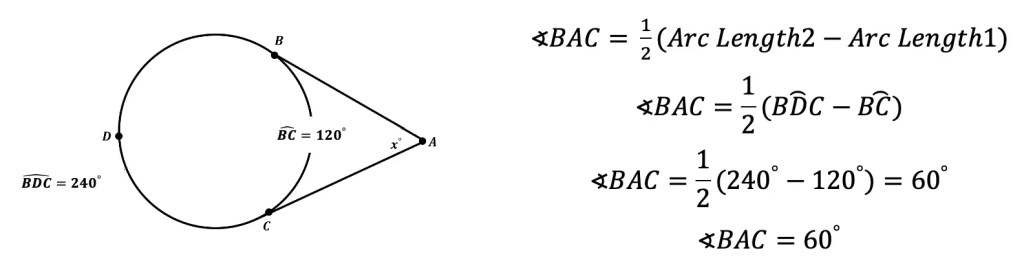
6. Two Secants: When two secants intersect outside the circle, it creates one angle and two intercepted arc lengths. The angle is equal to the difference between the intercepted arc lengths divided by two.
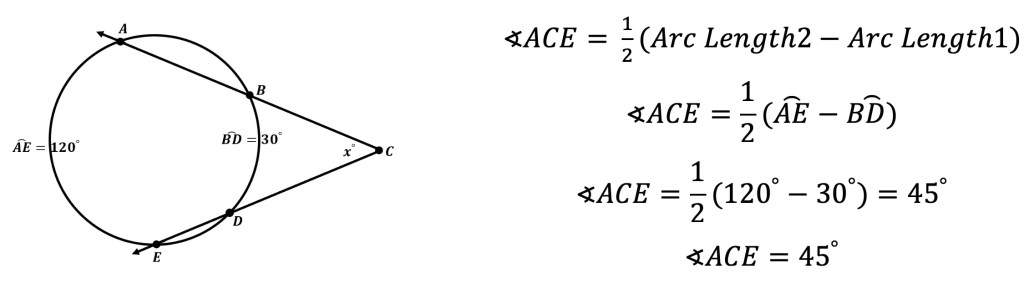
For more on Intersecting Secants, check out the video below and link here for practice questions!
7. Secant and Tangent: When an angle is formed by a secant and tangent it creates one angle and two intercepted arc lengths. The angle is equal to the difference between the intercepted arc lengths divided by two.
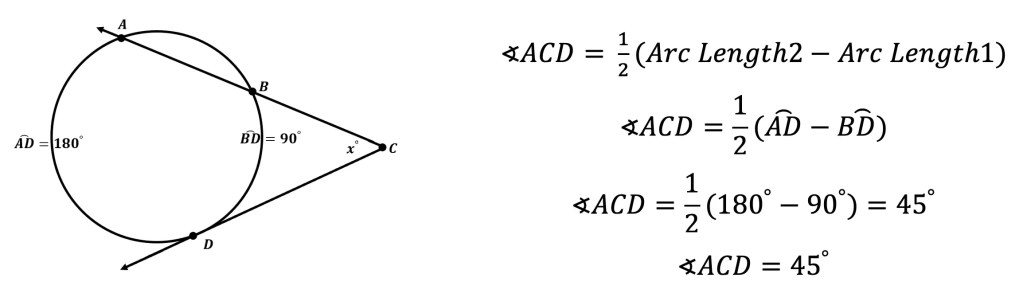
For more Secant & Tangent review, check out the video below!
Circle Theorems:
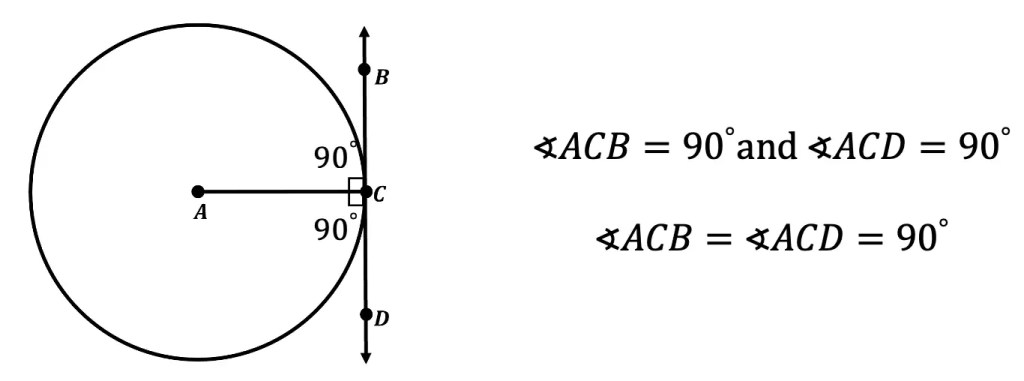
Theorem 1: In a circle, when an angle is formed by a tangent and radius it creates an angle. This happens always and every time!
Theorem 2: In a circles, inscribed angles that intercept the same arc, have equal angles. These types of overlapping arcs can also be known as “angles subtended by an arc.” In the example below, angle A and angle B are angles subtended by arc CD.
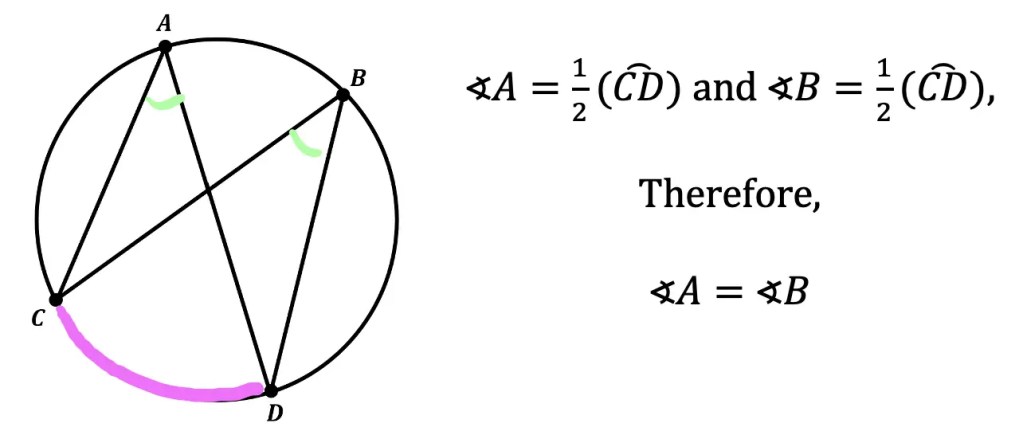
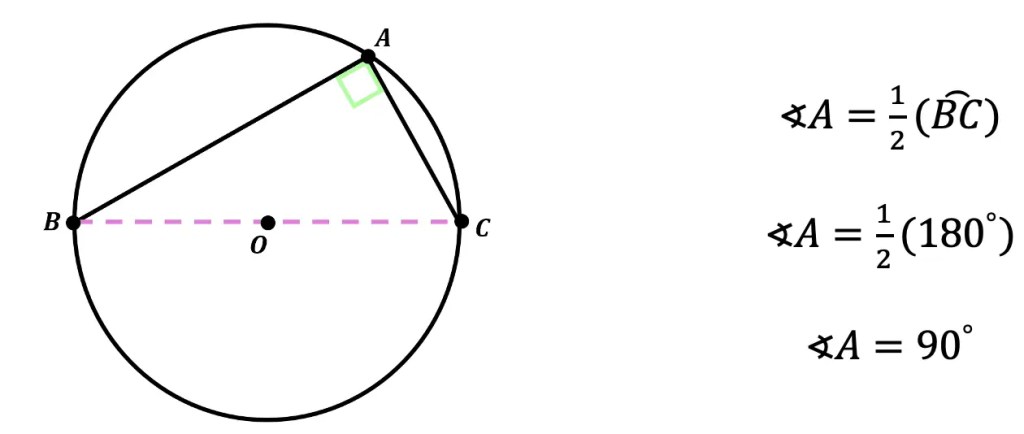
Theorem 3: An inscribed angles in a semi-circle is a right angle.
Theorem 4: When a quadrilateral is inscribed in a circle, opposite angles are supplementary (add to 180º). Notice below, opposite angles A and C are supplementary, adding to 180º.
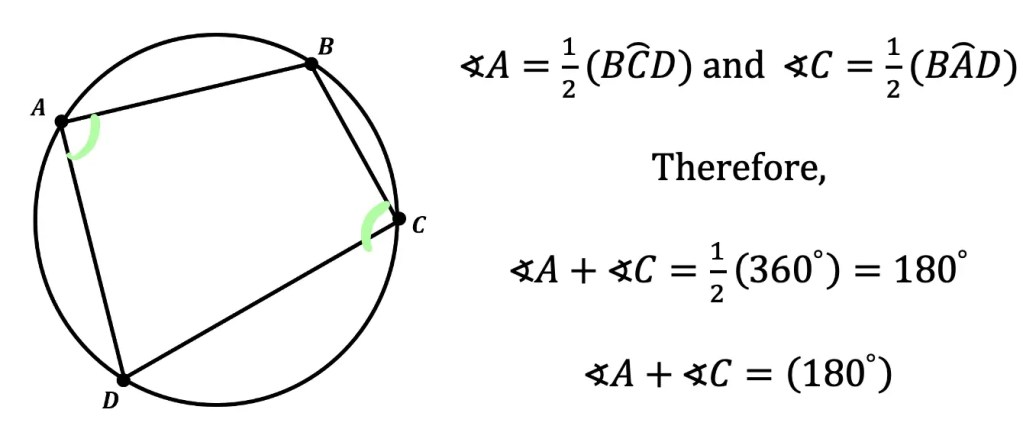
*Fun Fact! A quadrilateral inscribed in a circle is a called a Cyclic Quadrilateral!
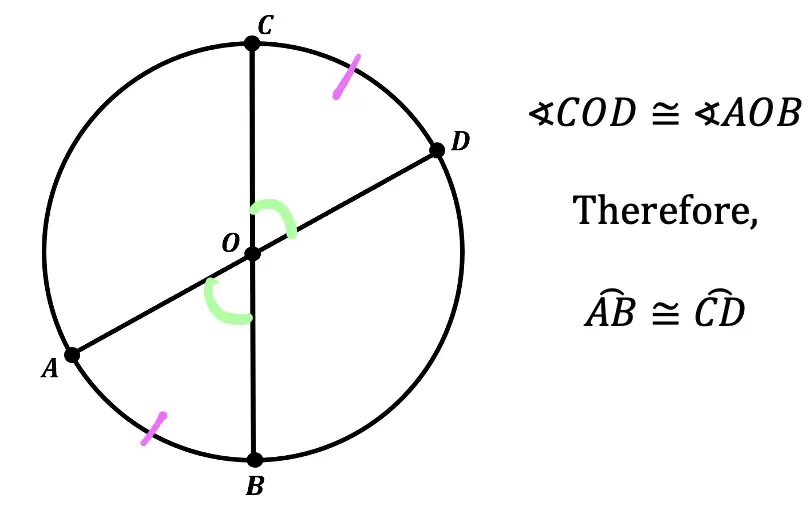
Theorem 5: In a circle, congruent central angles, also have congruent arcs (or vice versa).
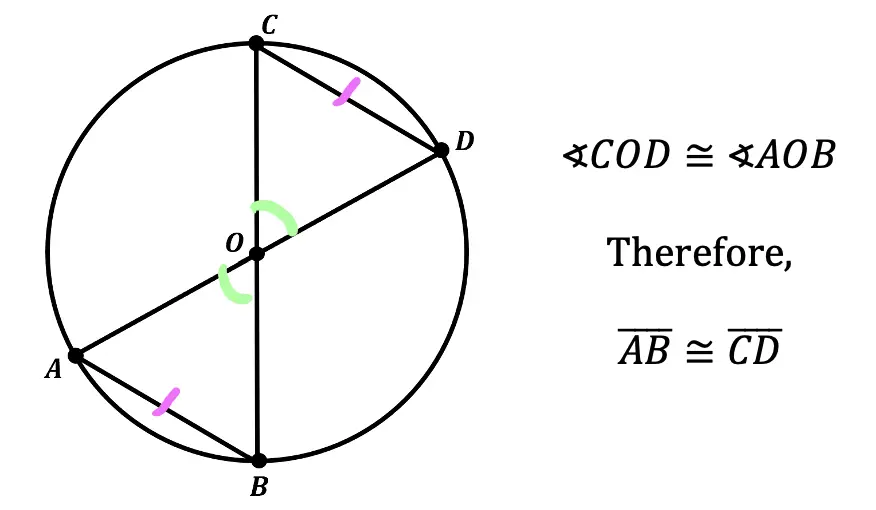
Theorem 6: In a circle, congruent central angles, also have congruent chords (or vice versa).
Now that wraps up all we need to know about circles, yay! Although we are done reviewing what we need to know, we must prepare for the questions that apply our new circle knowledge. One Example might go something like this:
Given circle R has arc BC=95º, two tangents AB and AC and two radii RB and RC, find the following angles and arcs.
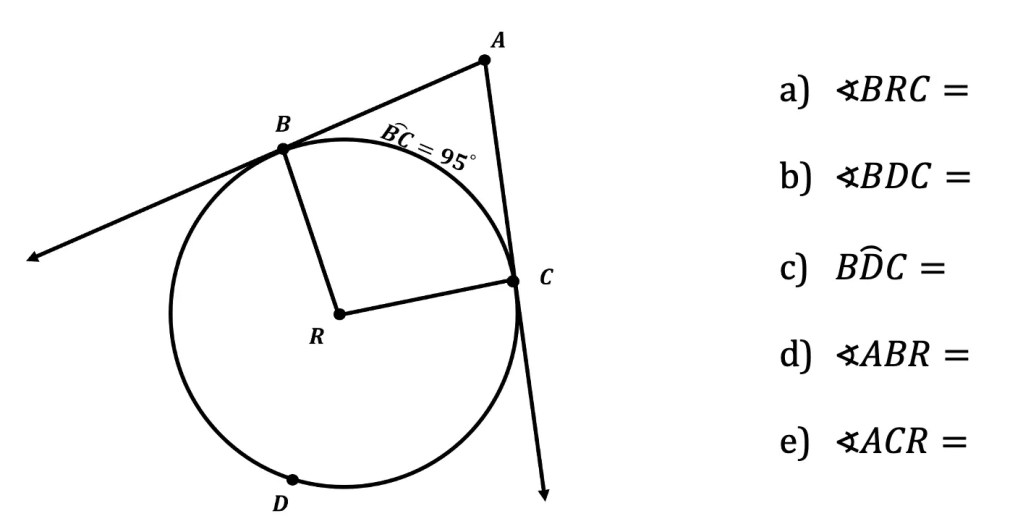
Before we just look at the solution, make sure to try this on your own! Remember all the answers to finding the arcs and angles of Circle R are based on the circle theorems and seven different ways of finding angles that we just went over in this post. So, go back if you need to, I know I needed to!
And now for that long-awaited Solution:
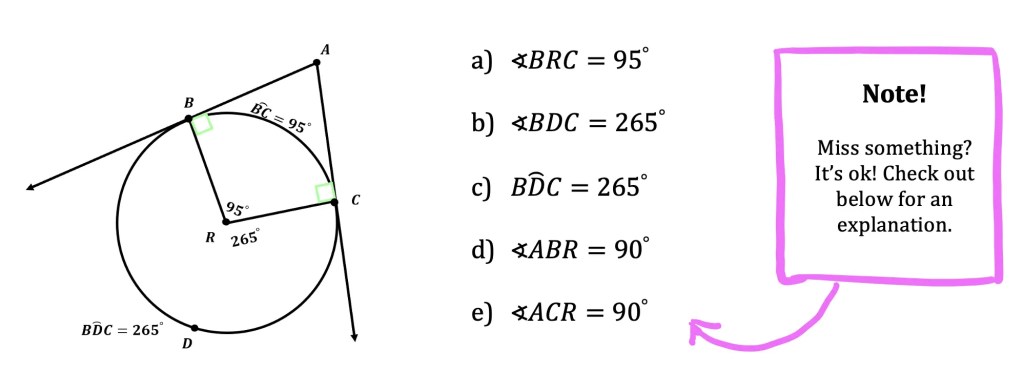
Explanation:

Still got questions? No problem! Check out the videos above or comment below for any questions and follow for the latest Free math lessons, videos, and practice questions! Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Tip! Also, don’t forget to check out the links found throughout this post for each related related lesson on central angles, inscribed angle theorems, intersecting secants theorem, and area of a sector, to dive even further into practice questions, videos, and more!
