Greeting math friends and welcome to MathSux! In today’s post, we are going to go over the Law of Sines! This is a great formula for finding missing angle and side information on a triangle that is NOT a right triangle, that is only if we are given ASA (Angle, Side, Angle) or AAS (Angle, Angle, Side) information of said triangle.
There is also something called the “ambiguous case” that happens when we have SSA (Side, Side, Angle) information of a triangle, and it is just as mysterious as it sounds. We can use the law of sine in the case of SSA to find missing angle and side information of a triangle as well, but there may be 0 triangles, 1 triangle, or even 2 triangles that exists in this case!
Sound confusing? Fear not, because we will cover everything in this post, including practice questions found throughout and at the bottom of this article. Happy calculating!
Law of Sines:
The law of sines tells us that in any triangle (non-right triangles included!), the ratio of a sin of an angle to the value of its corresponding side are the same for all three sides of a triangle. Check out the formula below:
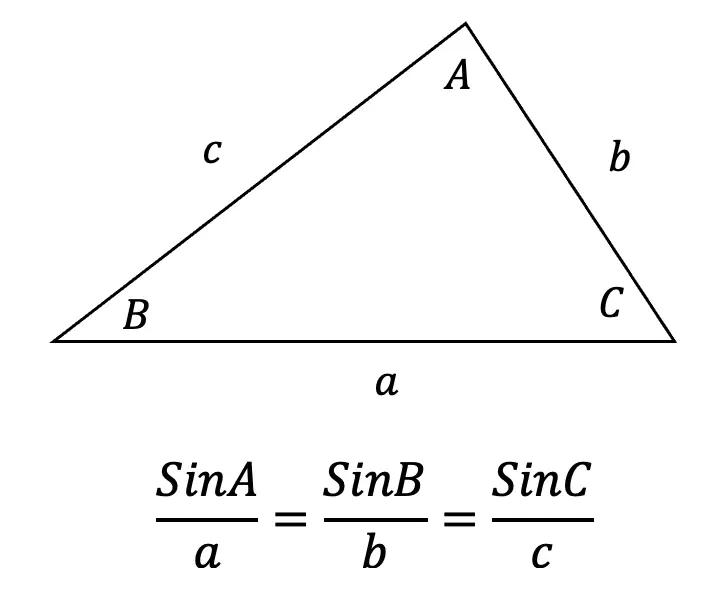
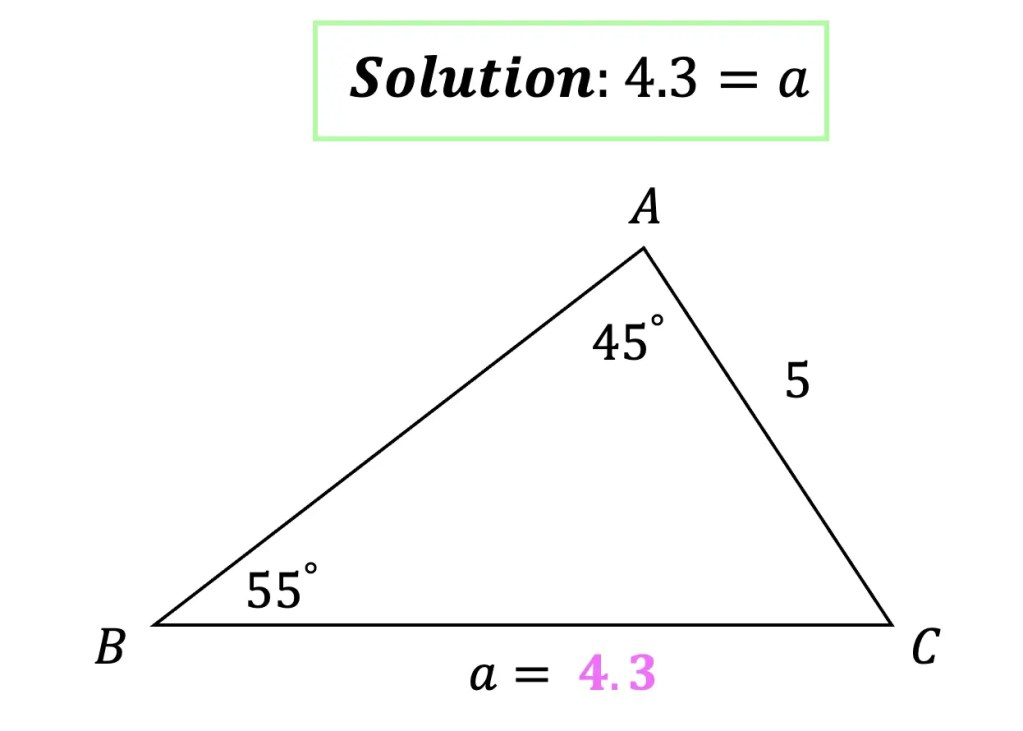
Example #1: AAS Find the value of the missing side
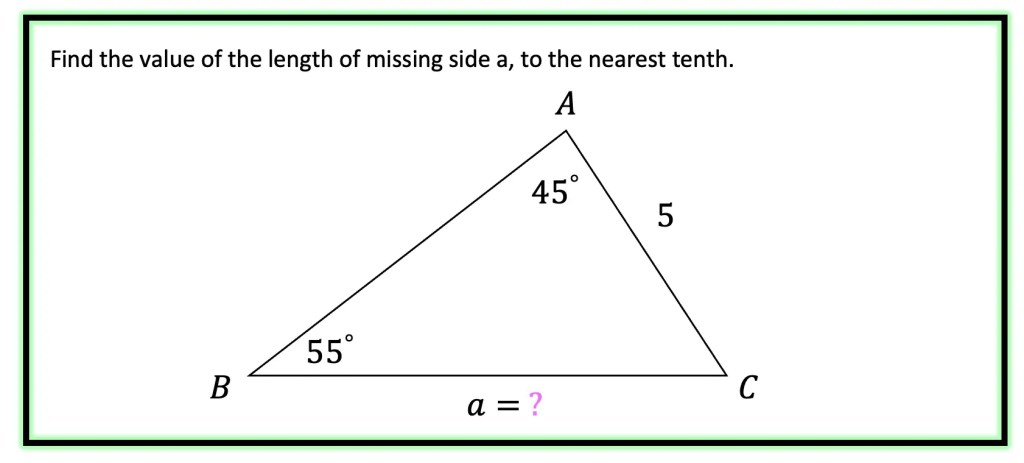
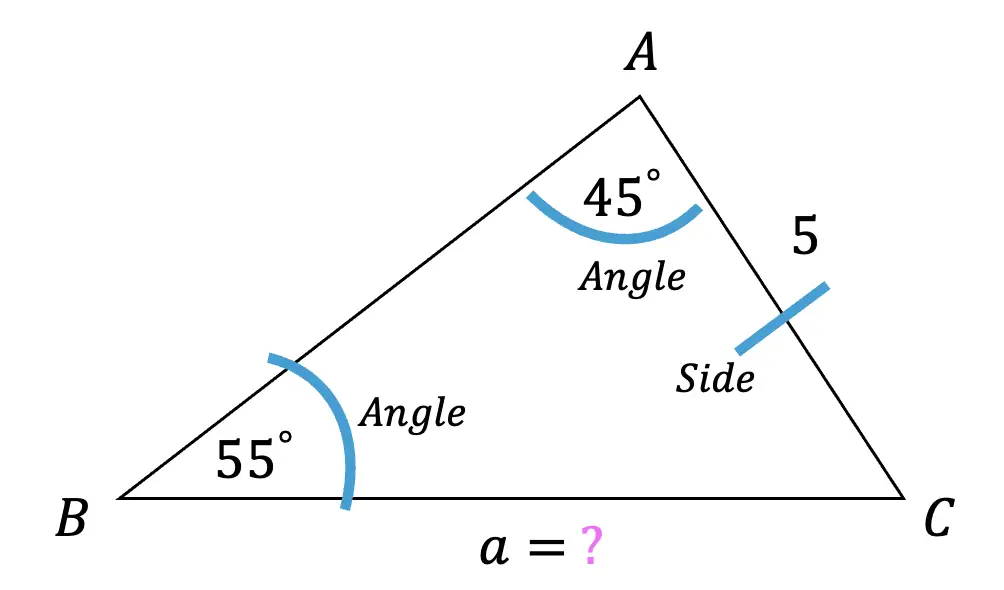
Step 1: First, let’s identify what type of information our triangle is providing us with. Notice that we are given angle A , angle B, and side b for AAS. Since our triangle contains AAS, we know we can apply the law of sine to find the missing side.
Step 2: Next, let’s write our law of sine formula and then plug in our given information. Notice we set up our formula where each side (a and b) and the sine of its opposite angle (Sin A and Sin B) represent the denominator and numerator respectively.
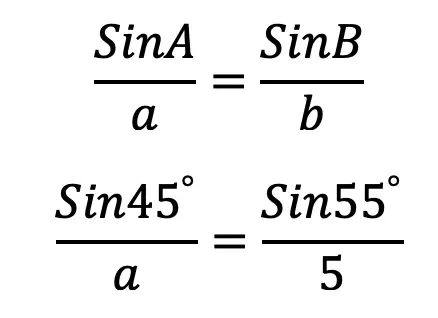
Step 3: Time to use some of our basic algebra and trigonometry skills and solve for unknown side length a by cross multiplying.
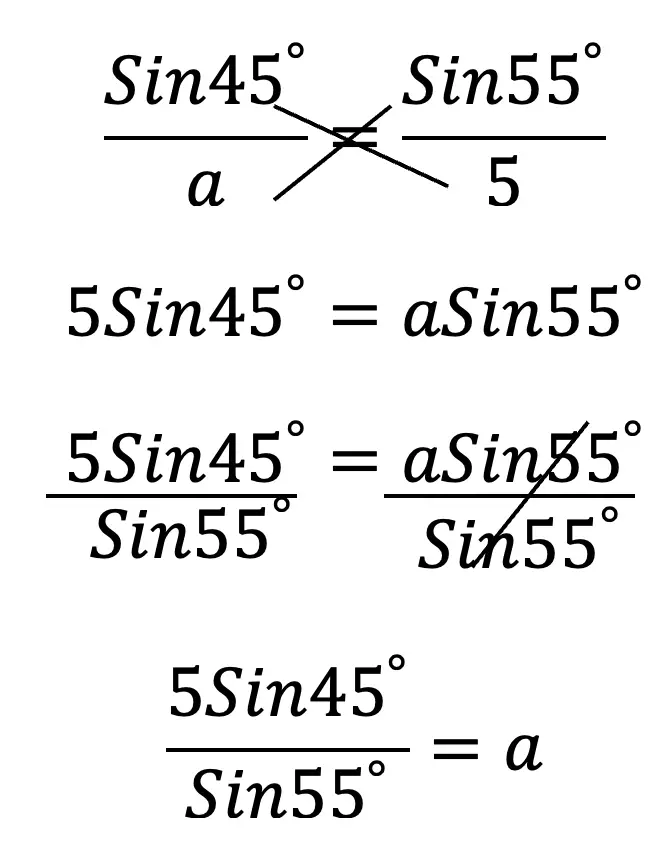
* Tip! Remember when plugging sin, sin-1, and all other trigonometric functions into your calculator, to be sure that you are in degree mode!
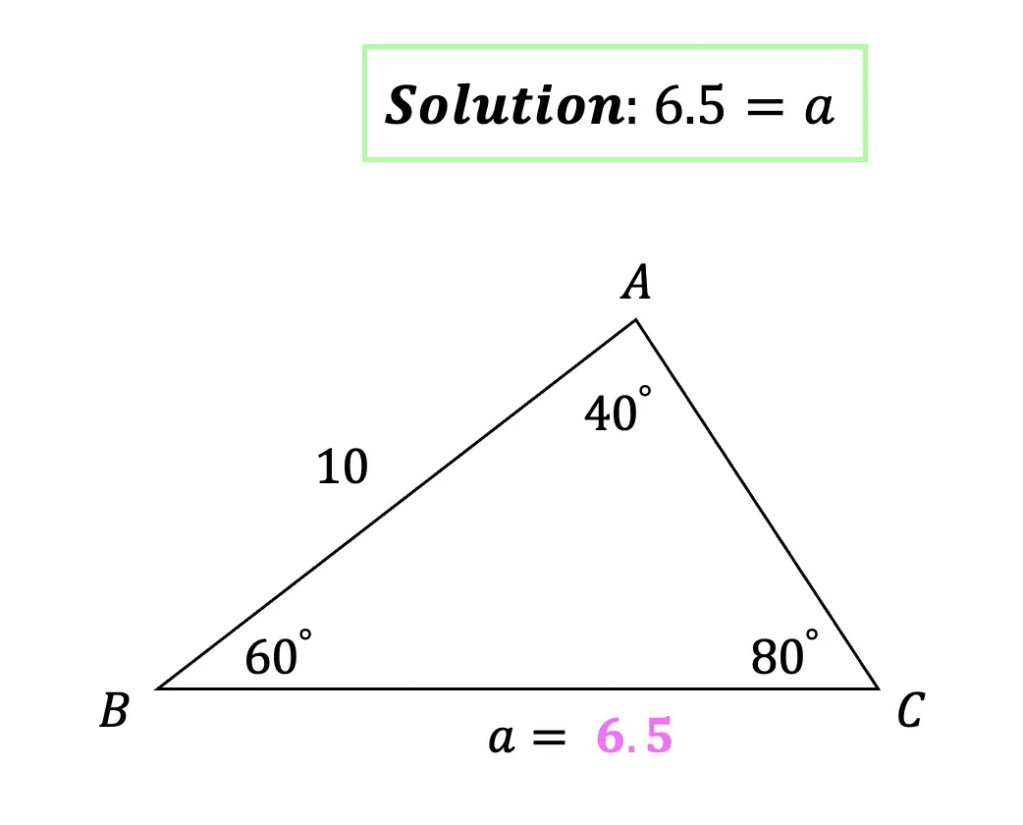
Example #2: ASA Find the value of the missing side

Step 1: First, let’s identify what type of information our triangle is providing us with. Notice that we are given an angle A, side c , and an angle B for ASA. Since our triangle contains ASA, we know we can apply the law of sine to find the missing side.
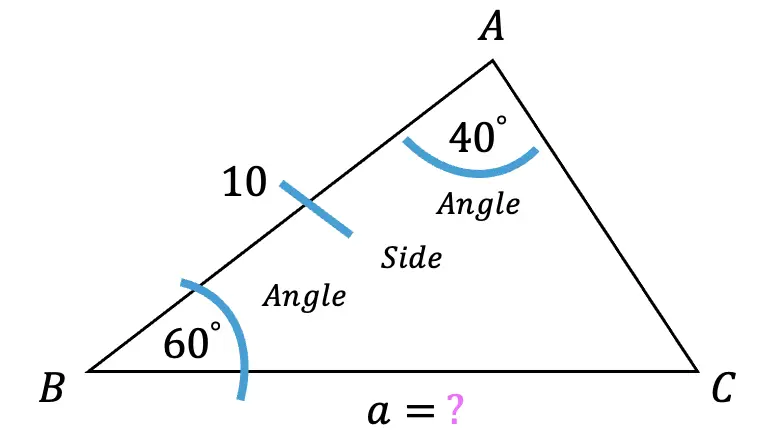
Step 2: Taking a look at the angles of our triangle, notice how side a is in between angle B and angle C. We have angle B, but notice the value of angle C is missing! So we first will need to find angle C. We can find the value of angle C, knowing that the interior angles of a triangle always add to 180º.
Angle C: 180º – (40º +60º) = 80º
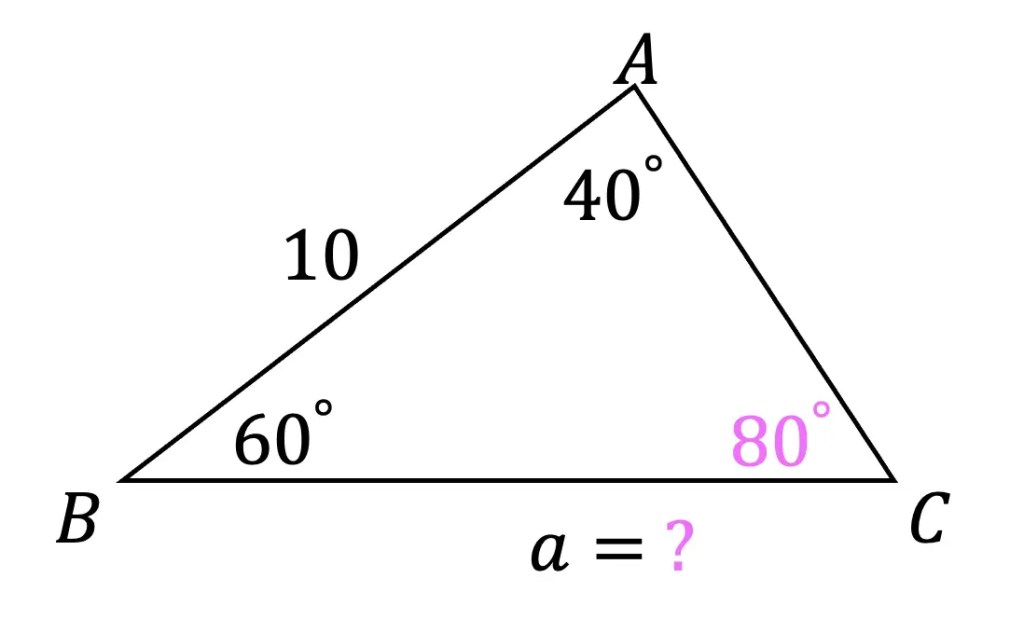
Step 3: Now that we have that missing angle value, we can find the length of side a. Let’s write our law of sines formula and then plug in our given information. Then we can cross multiply and use our knowledge of algebra and trigonometry to find the correct answer.
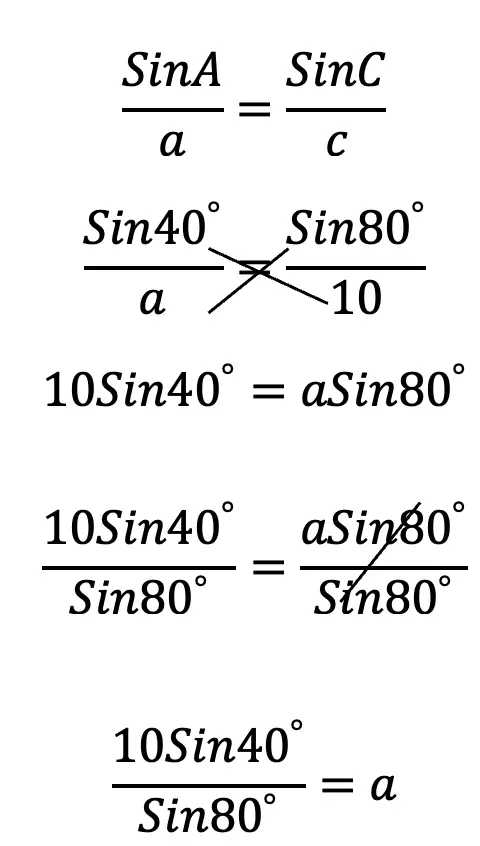
* Tip! Remember when plugging sin, sin-1, and all other trigonometric functions into your calculator, to be sure that you are in degree mode!
Think you are ready to master the law of sines on your own for AAS and ASA triangles? Try the following practice questions on your own to test your law of sines knowledge!
Practice Questions:
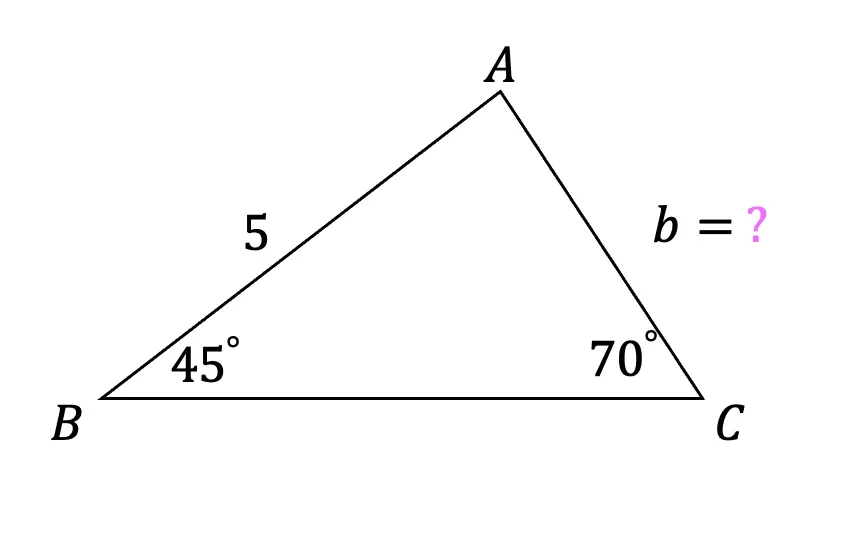
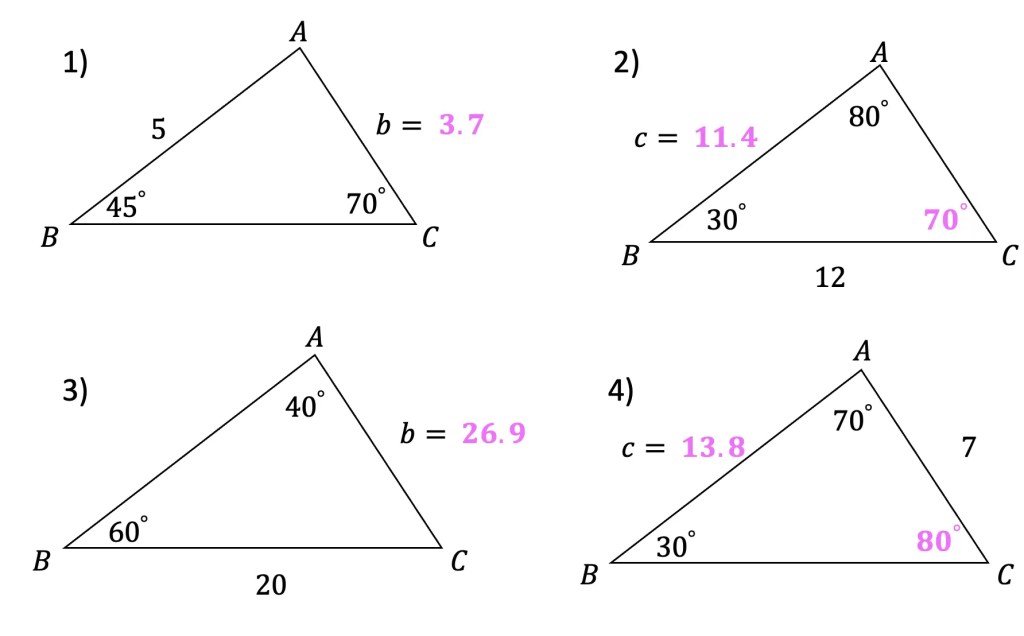
1) Find the value of missing side, b, to the nearest tenth.
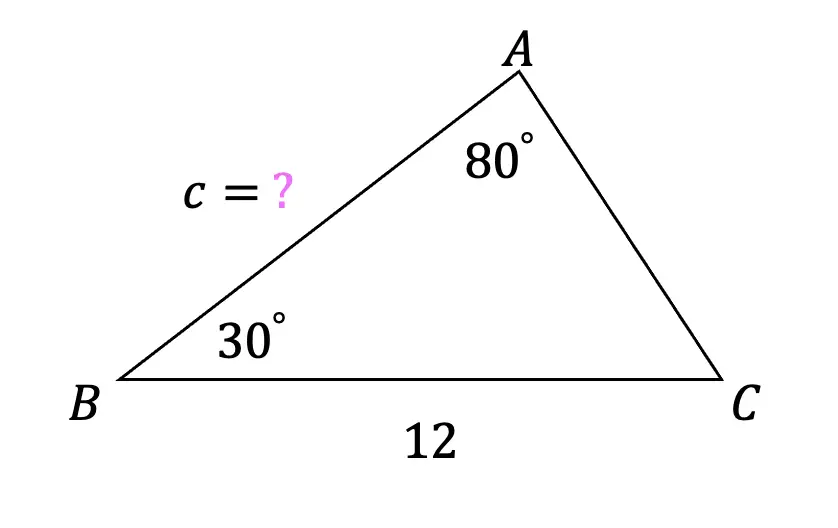
2) Find the value of missing side, c, to the nearest tenth.
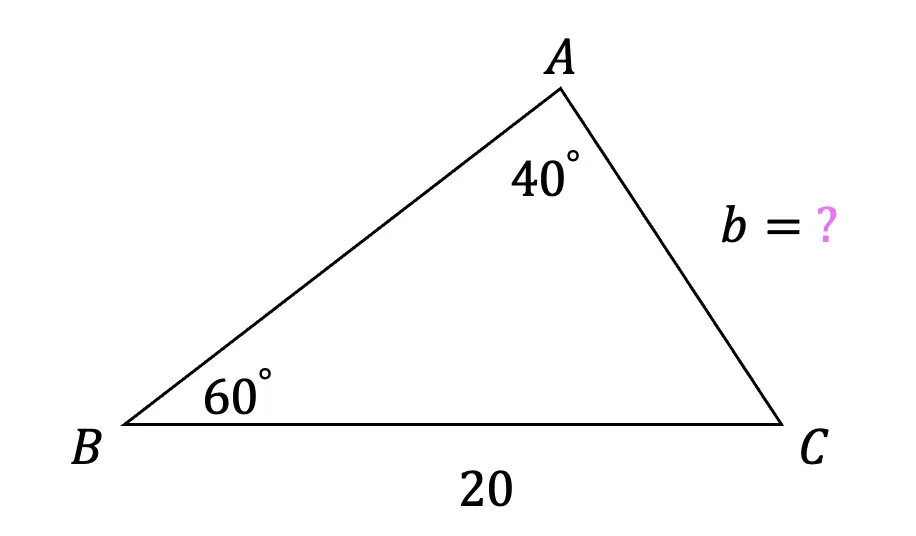
3) Find the value of missing side, b, to the nearest tenth.
4) Find the value of missing side, c, to the nearest tenth.
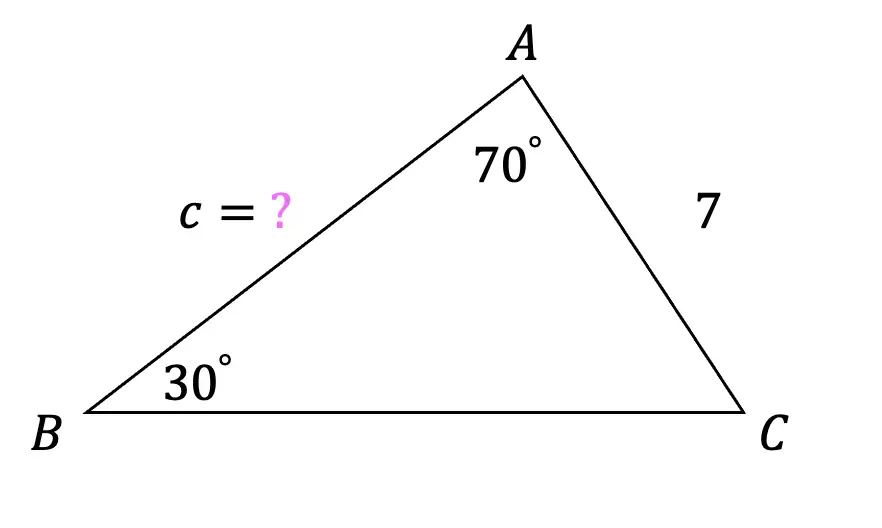
Solutions:
The Ambiguous Case – SSA and Law of Sines
So far, we’ve seen how to find a missing side using the law of sine when given ASA or AAS of a triangle. But now, we will see a special case scenario, otherwise known as the Ambiguous Case, where we are given SSA (Side, Side, Angle) of a triangle and must use the law of sines to see if there are potentially 0, 1, or 2 triangles that can potentially exist..
The Ambiguous case, is “ambiguous” because SSA is not enough information to find unknown angles and sides, as there can be more than one possible triangle with different angle measures. Although there is not enough information, SSA does tell us enough to infer all potential triangles (0,1 or 2) by figuring out what potential angles may or may not exist.
There are a lot of rules and visualizations associated with the ambiguous case that I will not be getting into here. If you would like to see more information and visualizations of the ambiguous case, please let me know in the comments. Let’s see how it works with the next example:
Ambiguous Case Example

Step 1: First, let us draw a triangle and fill in the information that has been provided to us, knowing angle A is 30º, side a is 10 and side b has a length of 15.
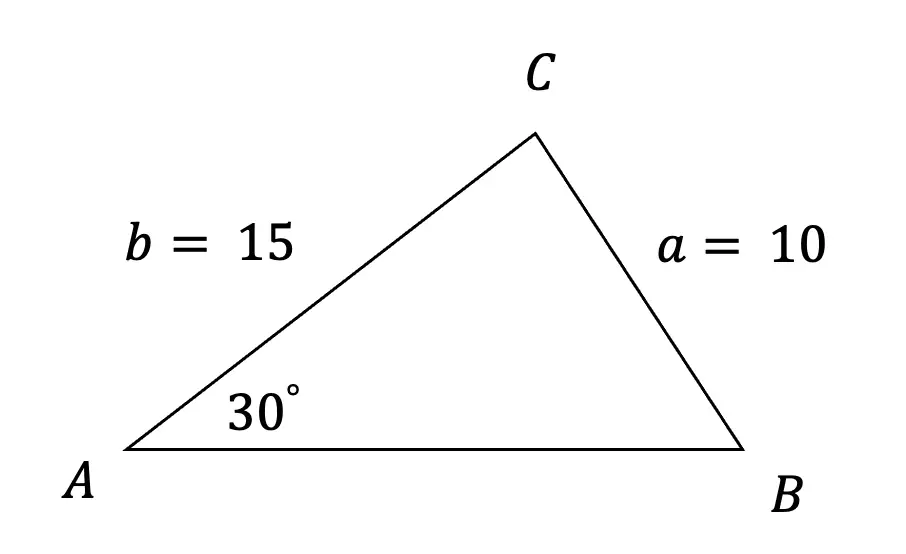
Step 2: Next, let’s identify what type of information our triangle is providing us with. Notice that we are given a side, side, and an angle for SSA. Since our triangle contains SSA, we know we can apply the law of sines and that this is going to be an ambiguous case, meaning there can be zero, one, or two potential triangles.
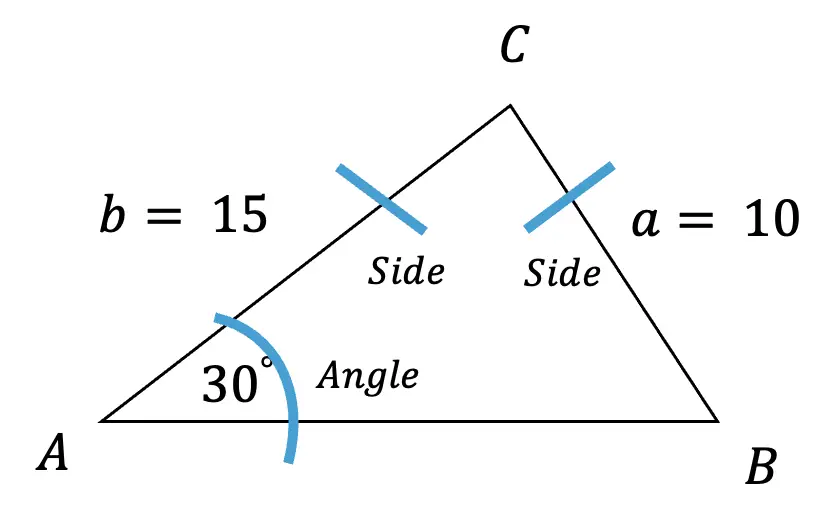
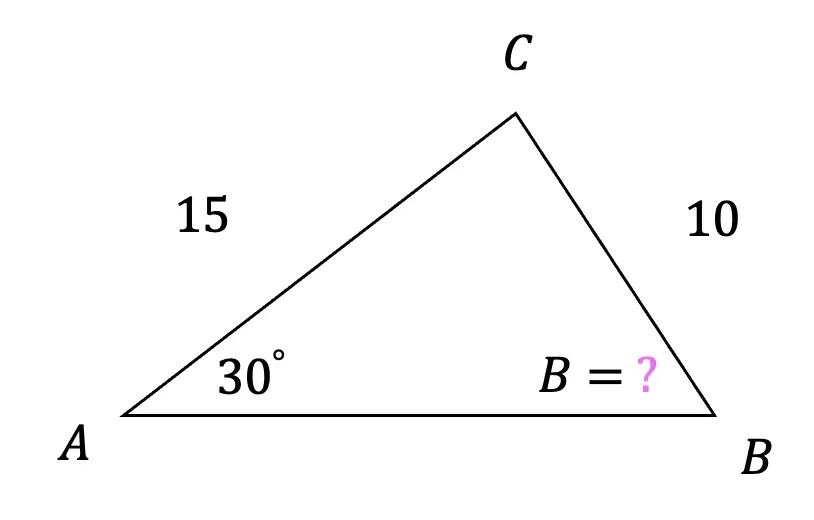
Step 3: Now, we can start off by using the law of sine to find the value of angle b. We want to find angle B because we already have the value of side length b, opposite our unknown angle B.
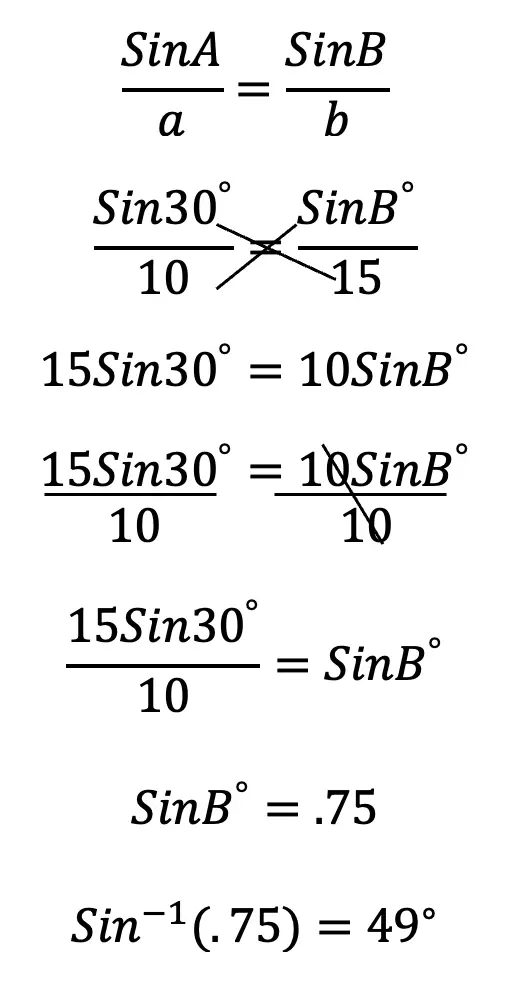
* Tip! Remember when plugging sin, sin-1, and all other trigonometric functions into your calculator, to be sure that you are in degree mode!
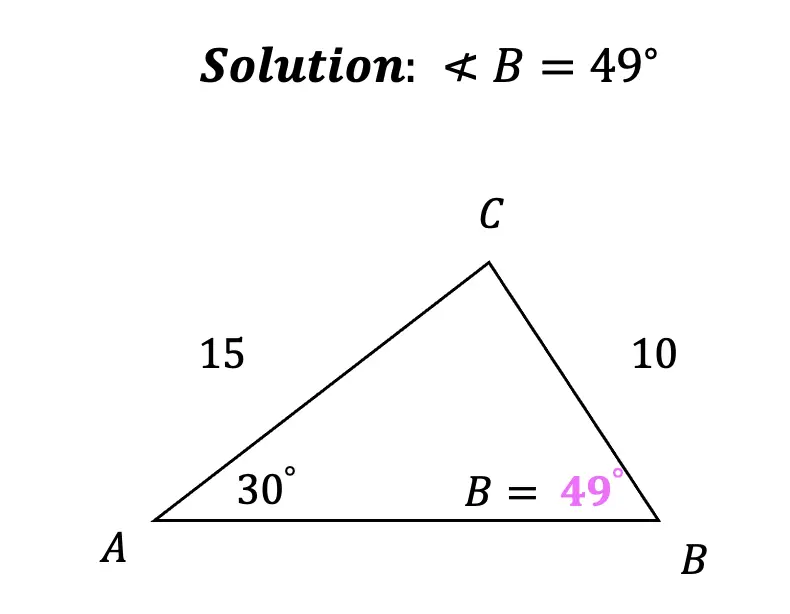
Step 4: But wait! We have found what appears to be value of unknown angle B, but since this is a SSA, ambiguous case, we are not 100% sure of our angle measure because of too many unknowns!
Why can there be more than one value for angle b?
Since we are given SSA of our triangle, that leaves too many unknown values not just for angle B, but also for unknown values angle C, and the length of AB. This leads us to having more than one possible angle value for angle B.
Does one triangle exist? Yes!
We can see that one triangle exists using our found angle, angle b=49º. Based on this, we can infer what angle C would be, knowing that the interior angles of a triangle add to 180º.
Angle C= 180º – (49º+30º) = 101º
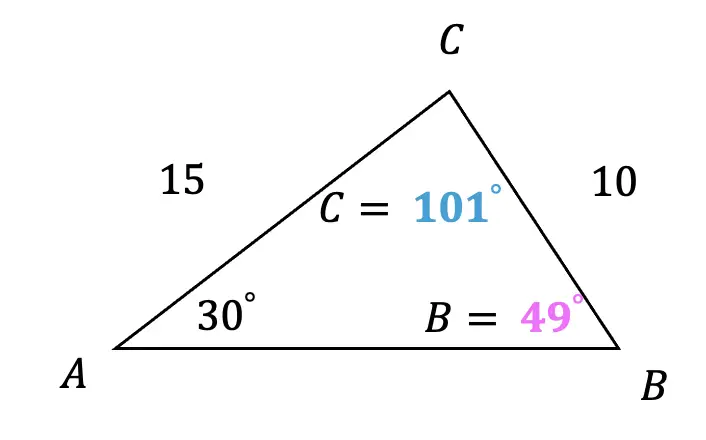
Do two Triangles exist? Yes!
Since our angle B technically can have two values, we can once again look to the unit circle and remember that sin is positive in quadrant 2 (sin must be positive since we are dealing with the law of sines and triangles). Knowing this we can use our reference angle 180º – θ, to find the potential bonus value for angle b, plugging in the angle value we found previously for angle B= 49º for θ.
Alternate value for angle B = 180º – θ = 180º – 49º = 131º
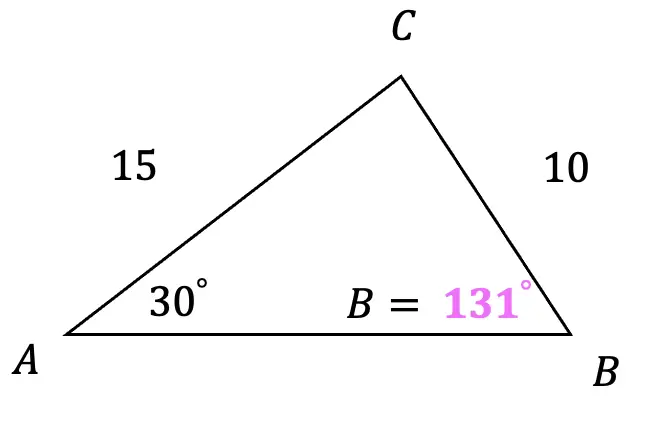
Based on this, we can infer what angle c would be, knowing that the interior angles of a triangle add to 180º.
Alternate value for angle C = 180º – (30º + 131º) = 19º
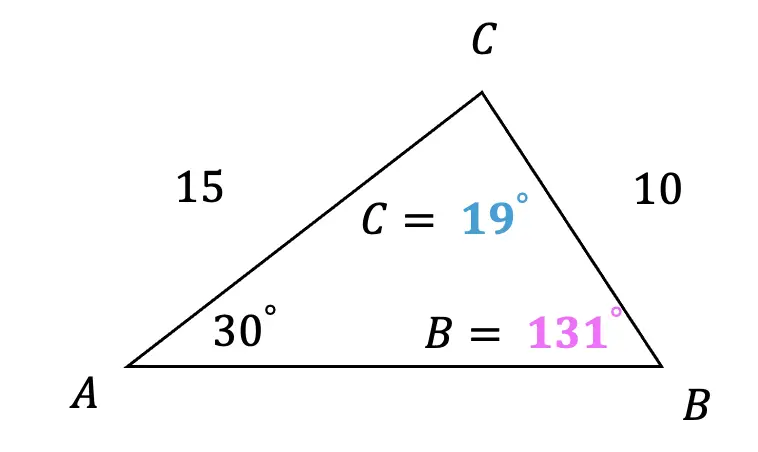

Note! In this case there are two triangles, but please note that that will not always be the case and the way to know that is to make sure all the angles of your second triangle add up to 180º and nothing over!
Think you are ready to give the ambiguous case and the sine rule a spin? Try the following practice questions on your own!
Practice Questions:
How many triangles can be constructed with the given measures?

Solutions:
- 2 Triangles
- 1 Triangle
- 2 Triangles
- 1 Triangle
Still got questions on the law of sine? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! If you want to check answers on your homework, check out the law of sines calculator here! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube

Good one
Thank you!