Law of Cosines

Greeting math friends and welcome to MathSux! In today’s post, we are going to cover the Law of Cosines! Otherwise known as the cosine rule, this is a great formula for finding missing angle and side information on a triangle that is NOT a right triangle when we have SAS or SSS information about the triangle in question. This formula is much more straight forward when compared to the law of sines, so if you have already mastered that formula, the law of cosines should be a breeze! Also, don’t forget to check out the practice questions at the end of this post to test your knowledge of the law of cosines. Happy calculating!

Law of Cosines:

The law of cosines allows us to find missing sides and angles of any non-right triangle (a.k.a an oblique triangle) where we are given SAS or SSS information about the triangle in question.

If you take a peak below at the law of cosines, notice that it can be derived from the Pythagorean theorem, as it is reminiscent of the classic formula we all know and love, a² + b² = c².

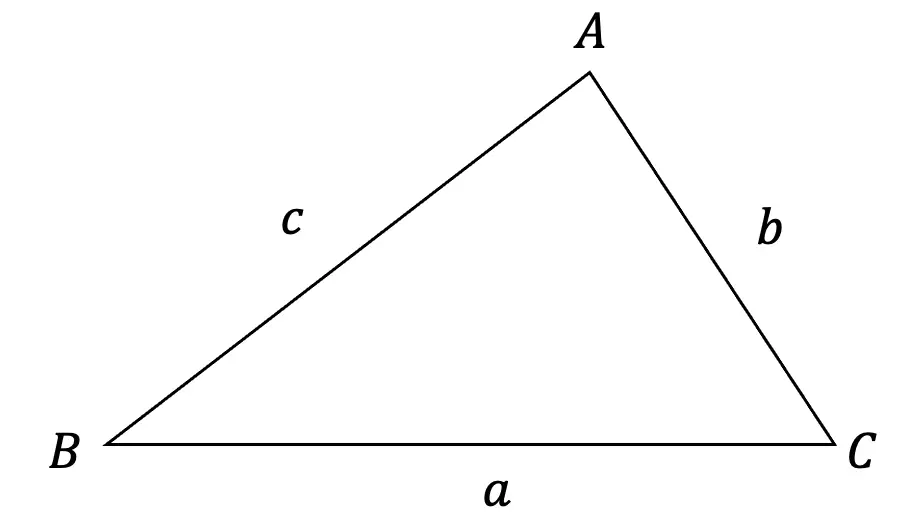
Also, notice each angle is across its opposite side (Angle A is opposite side a, Angle B is opposite to side b, and Angle C is opposite to side C).

a² = b² + c² -2bcCosA

b² = a² + c² -2acCosB

c² = a² + b² -2abCosC

To find Angles we can also derive and use the following formulas based on the law of cosines from above:

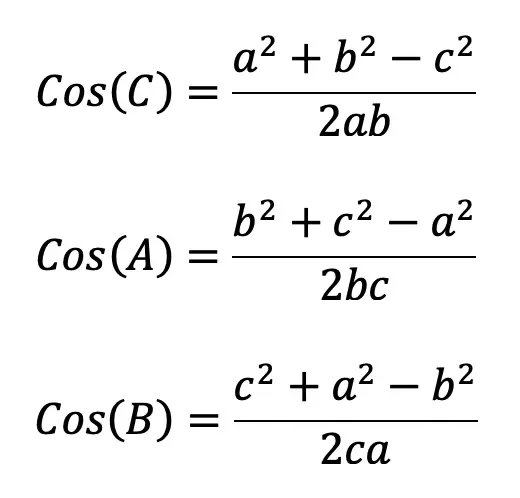
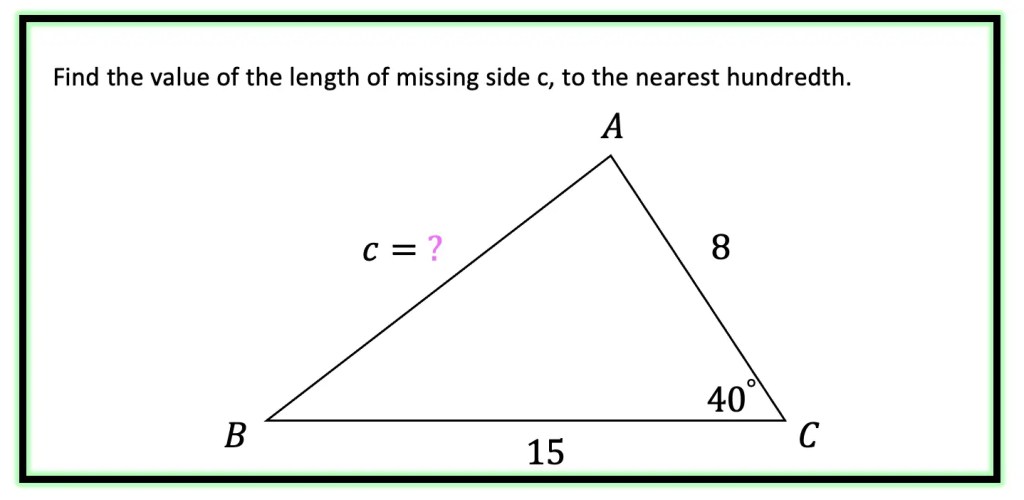
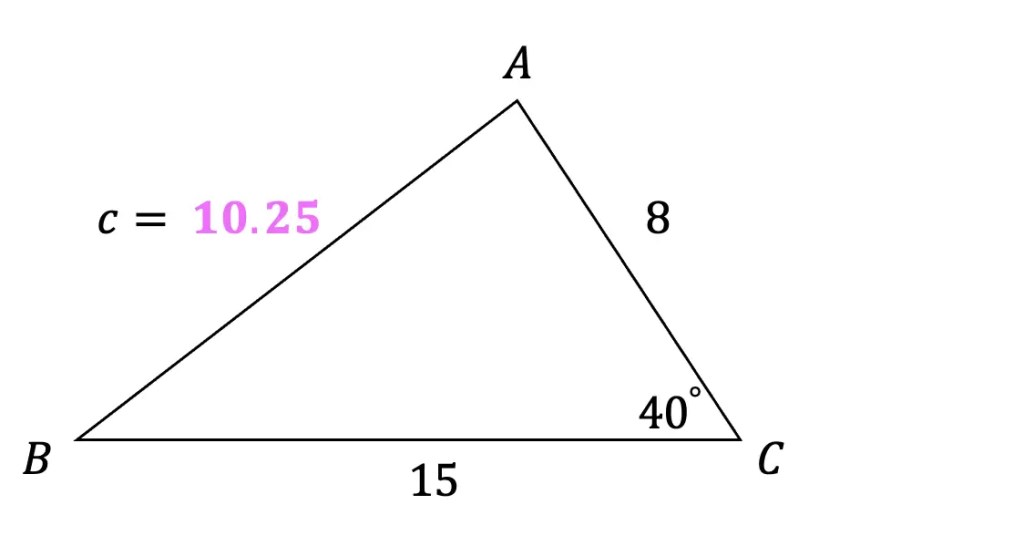
Example #1: SAS Find the value of the missing side.

We can use the law of cosines to find missing sides when we are given an oblique triangle that has a side, angle, and side (SAS) information.

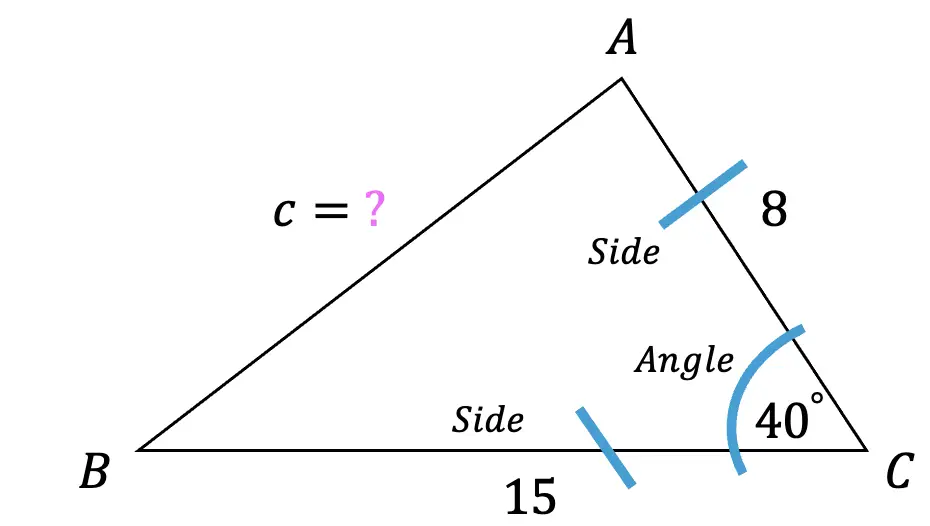
Step 1: First, let’s identify what type of information our triangle is providing us with. Notice that we are given a side, an angle, and a side for SAS. Since our triangle contains SAS, we know we can apply the cosine rule to find the value of unknown side c.

SAS

Step2: Next, let’s write out our law of cosines formula to find the value of length c and plug in our given information to solve for c. In this case we can plug in for side a=10, side b=8, and opposite side c we have angle c=40º.

Remember to take the square root of both sides of the equation to get our solution for unknown side c!

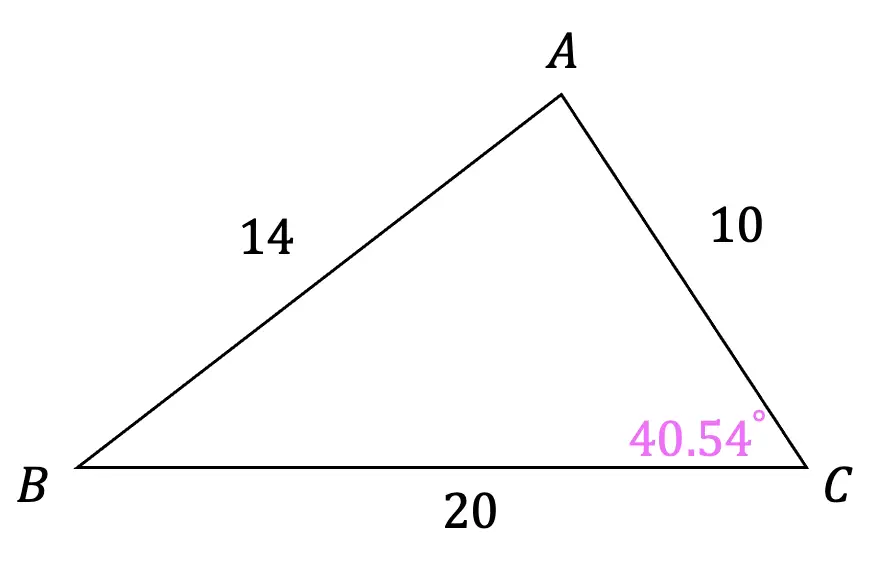
Example #2: SSS Find the value of the missing angle.

When we want to find the value of a missing angle and are given SSS information of a triangle, we can either use the original law of cosines formula and use our knowledge of algebra and trigonometry to solve for the unknown angle, or, we can also a different version of the cosine rule shown below. Either method works and will give you the correct answer, the choice is up to you!

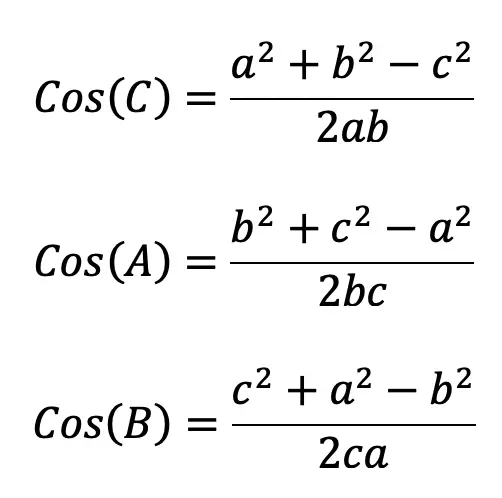
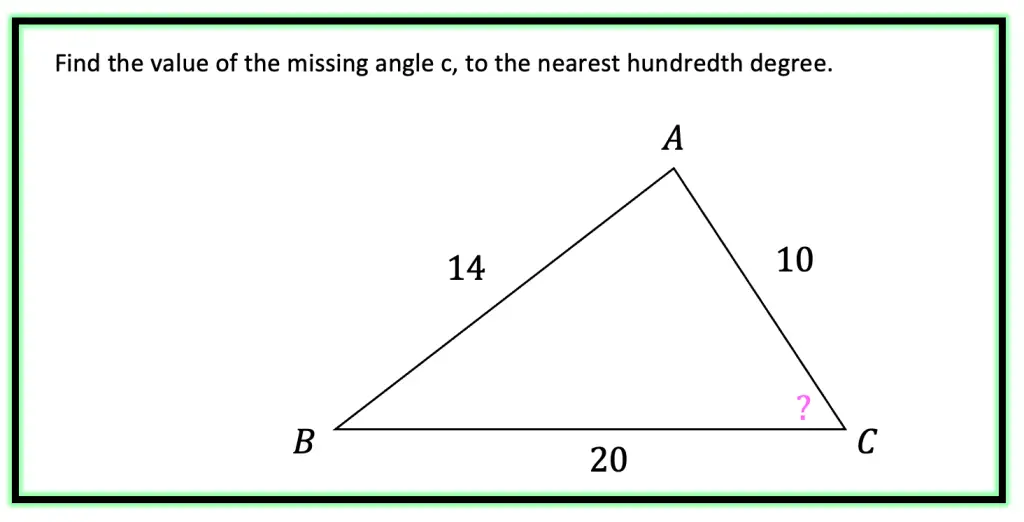
Step 1: First, let’s identify what type of information our triangle is providing us with. Notice that we are given a side, side, and another side for SSS. Since our triangle contains SSS, we know we can apply the cosine rule to find the value missing angle C.

SSS

Step 2: Next, let’s write our law of cosines formula and then plug in our given information. In this example, I will be using the original formula and then using algebra and trigonometry to find the correct answer, but feel free to apply one of the angle formulas above and see if you get the same answer!

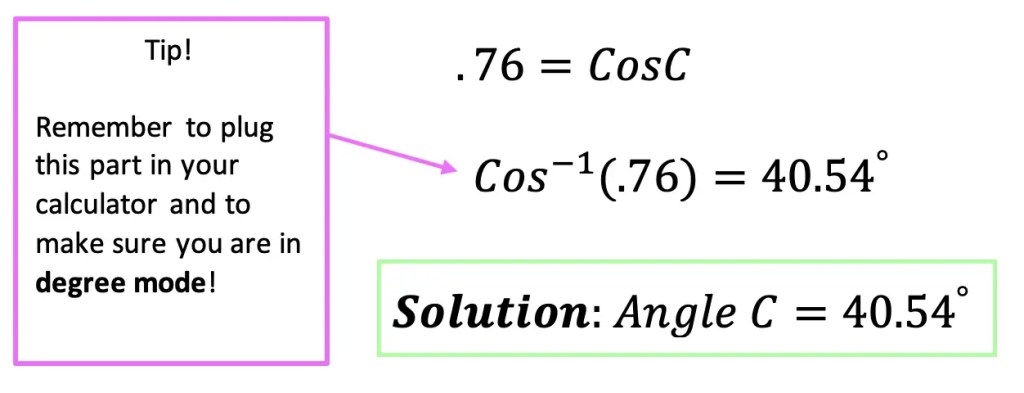
Since we want to find the value of angle C, we will be using the formula that is set equal to C²:

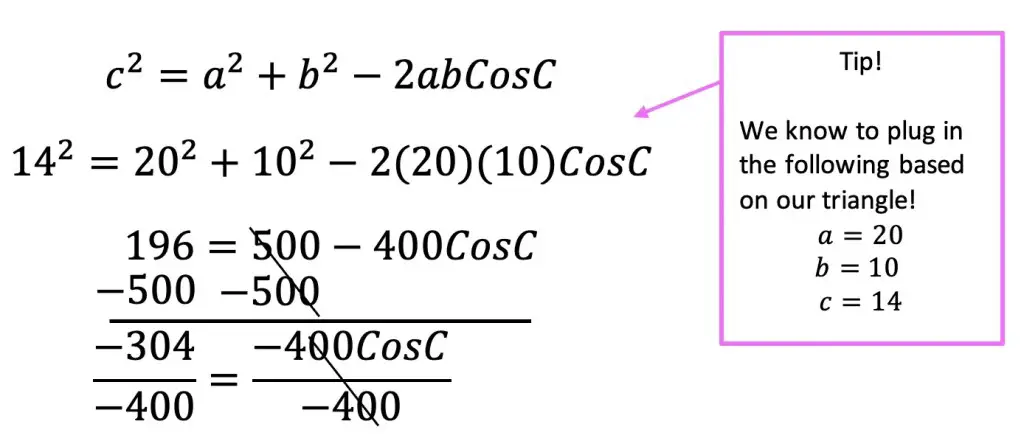
Think you are ready for more!? Try answering the following practice questions on the cosine rule on your own to truly master this formula! Then check your answers with the solutions below.

Practice Questions:

1) Find the value of missing side c, to the nearest hundredth.

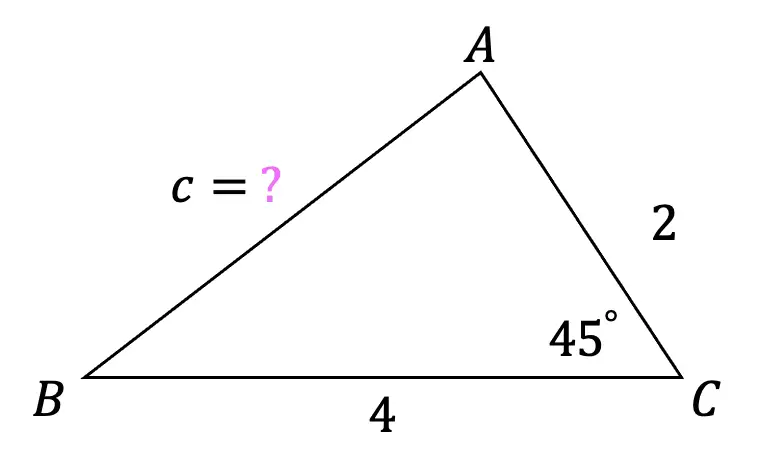
2) Find the value of missing side a, to the nearest hundredth using the cosine formula.

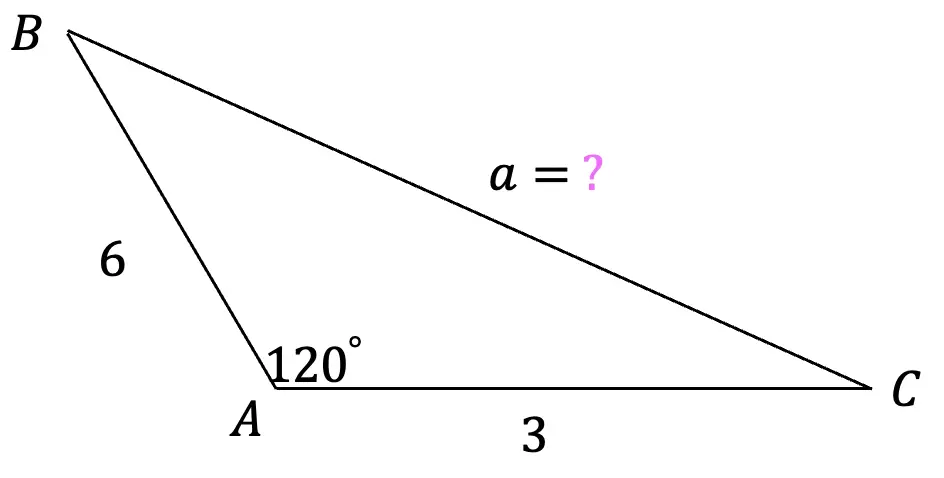
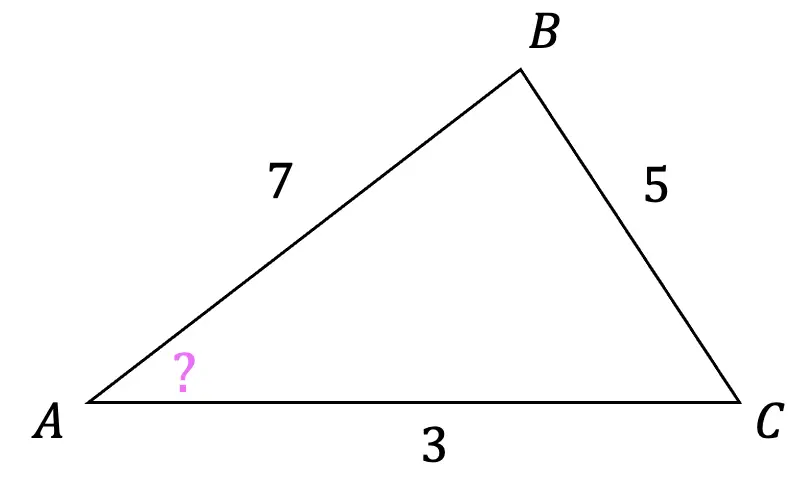
3) Find the angle measure of unknown angle A, to the nearest degree using the cosine rule.

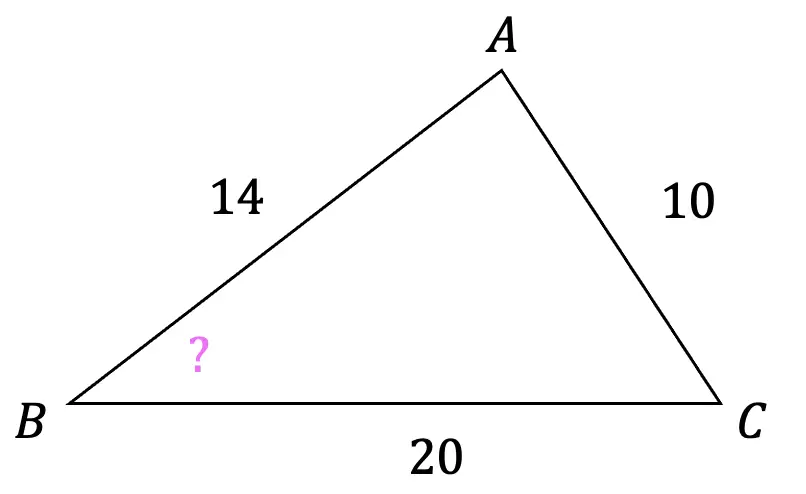
4) Find the value of missing angle B, to the nearest hundredth using the cosine rule.

Solution:

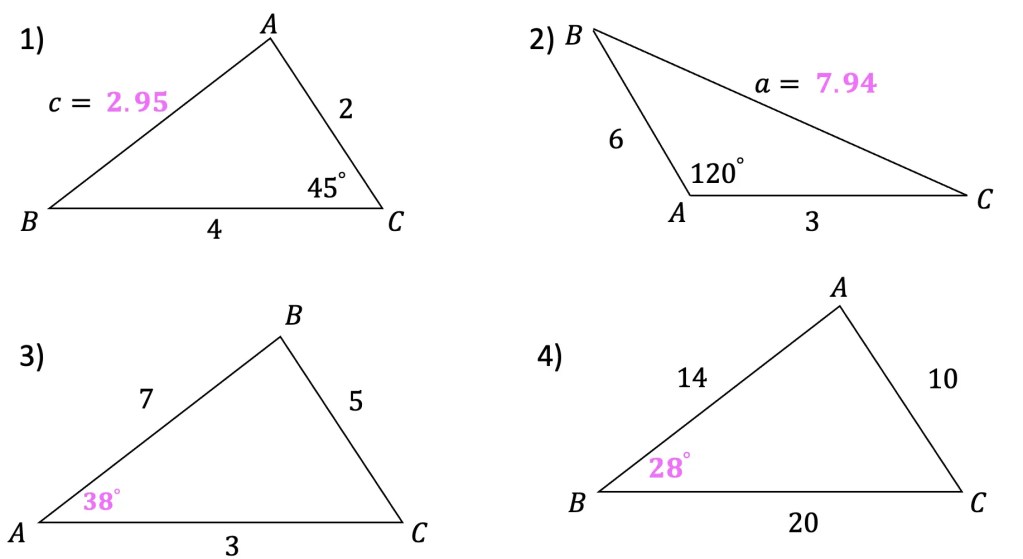
Still got questions on the law of cosines? Would you like to see how the cosine rule can be derived from the pythagorean theorem? Don’t hesitate to comment with any questions! If you want to check answers on your homework, you can also check out the law of cosines calculator here! And if you’re looking for more on trigonometry check out the related posts below.Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube