Greetings math folks! For anyone familiar with trigonometry and SOH CAH TOA trigonometric ratio you should know that there is something special about right triangles. We are about to learn more about right triangles, as there are two distinct types of special right triangles in this world that we need to know, this includes the 45 45 90 triangle and the 30 60 90 triangle. In this post, we are going to go over the 45 45 90 special right triangle! If you are looking for the other very famous special triangle, (30 60 90), check out this post here.
With the help of this special triangle, we are going to see how to find the missing sides of a right triangle when given only one of its lengths (and the angles of the right triangle given are 45 45 90). For even more examples, check out the video and practice questions below and at the end of this post. Happy calculating! 🙂
45 45 90 Right Triangle Ratio:
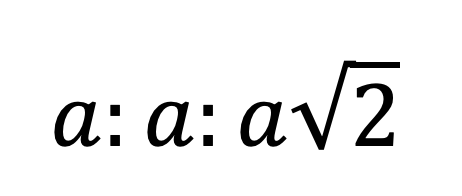
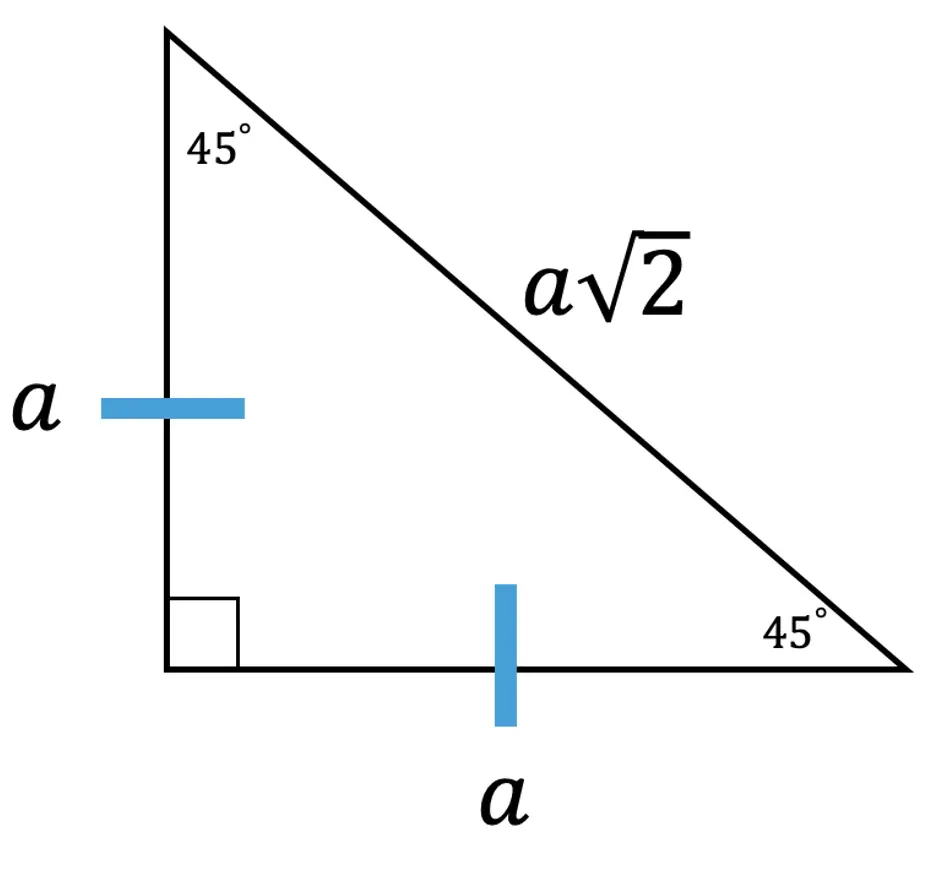
Looking above at our 45 45 90 special triangle, notice it contains one right angle and 2 equal angles of 45 degrees. Based on these angle proportions, we are able to infer information about each sides length, thats where our ratio comes in!
45 45 90 Triangle – Why is it special? Where did come from?
45 45 90 special right triangles are “special” because they are a type of Isosceles Right Triangle, meaning they have two equal sides (marked in blue below). If we know that the isosceles triangle has two equal lengths, we can find the value of the length of the hypotenuse by using the Pythagorean Theorem based on the other two equal sides. Check out how we derive the 45 45 90 ratio below!
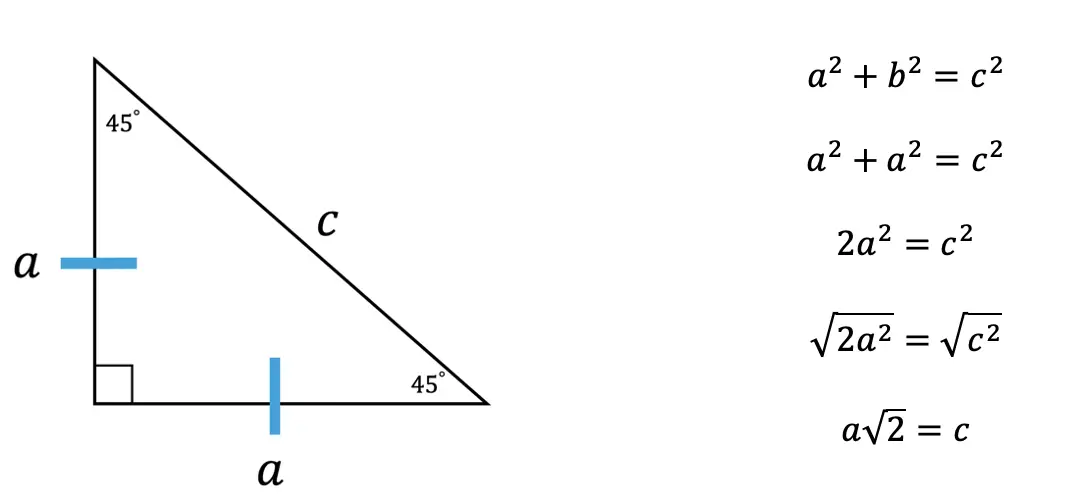
Notice, we started with the Pythagorean Theorem, then filled in our variables based on each given sides length. Next, we combined like terms and then took the square root of each side of the equation. Lastly, we found the value of hypotenuse, c, based on the other two legs, which is equal to the length of a times radical 2.
Now that we know the length of the hypotenuse in terms of each sides length a, we can re-label our triangle. Since we found the length of the hypotenuse in relation to the two equal legs, notice that this creates a ratio that applies to each and every triangle out there!
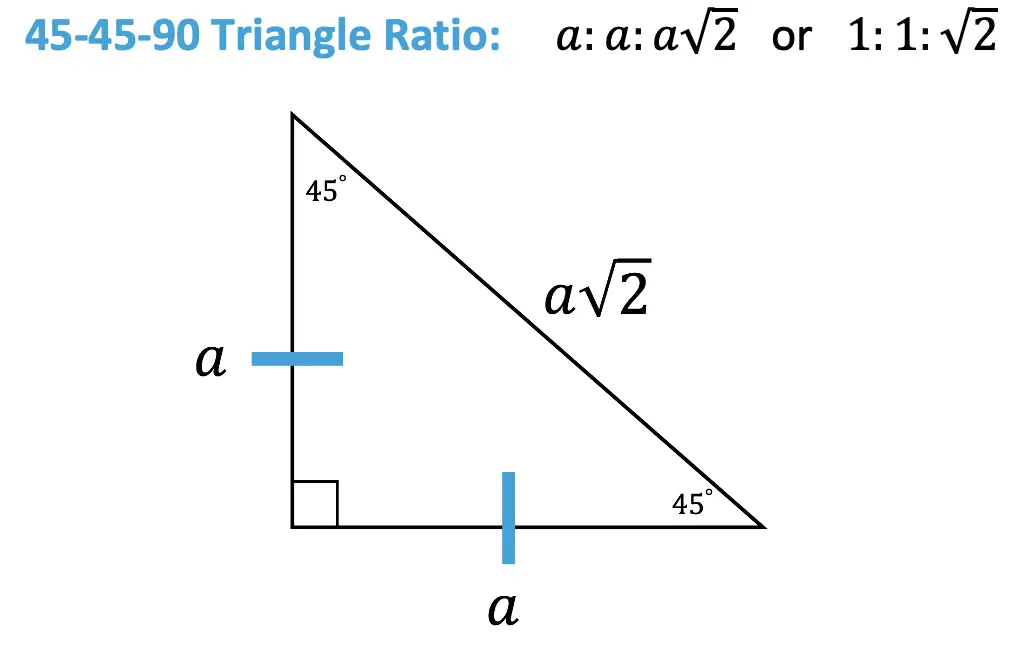
How do I use this ratio?
Ok, great we have derived the 45 45 90 ratio, but what do I do with this thing and how do I use it?
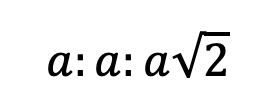
Knowing the above ratio, allows us to find the length of any missing side of a 45 45 90 special triangle (when given the value of one of its sides).
Let’s now try some 45 45 90 right triangle examples with missing sides below:
Example #1:
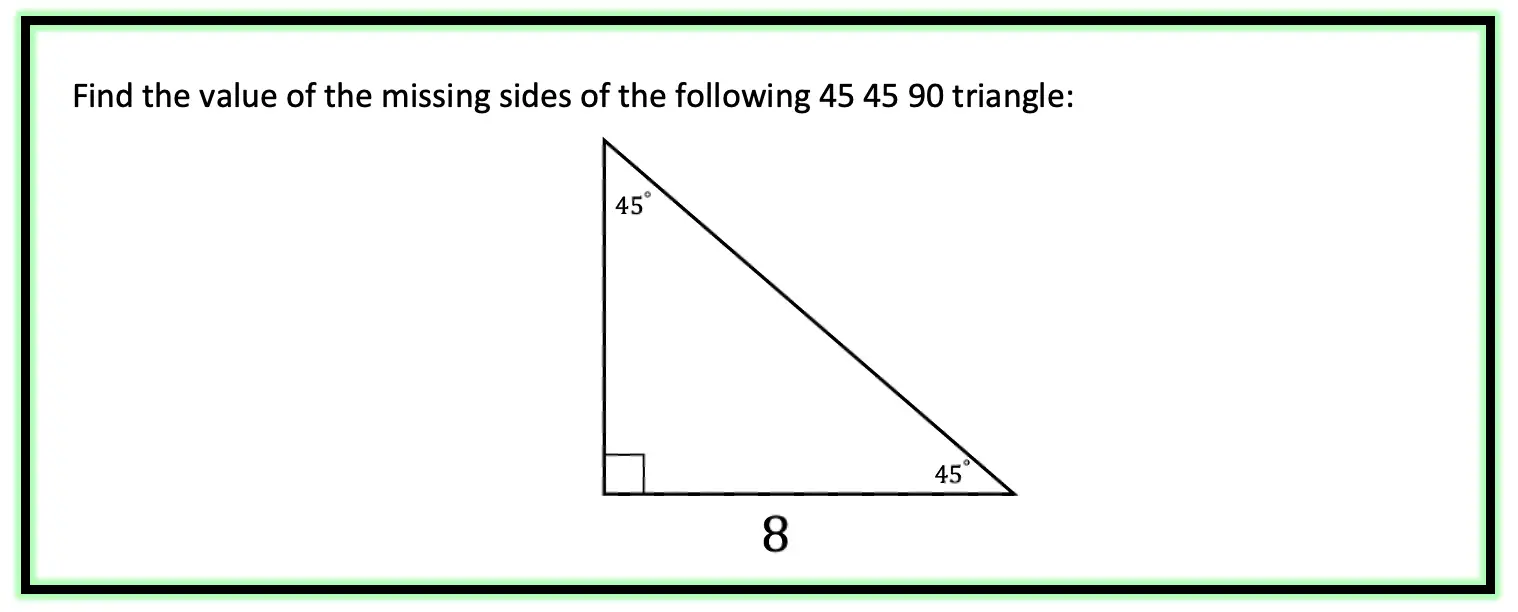
Step 1: First, let’s look at our ratio and compare it to our given right triangle.
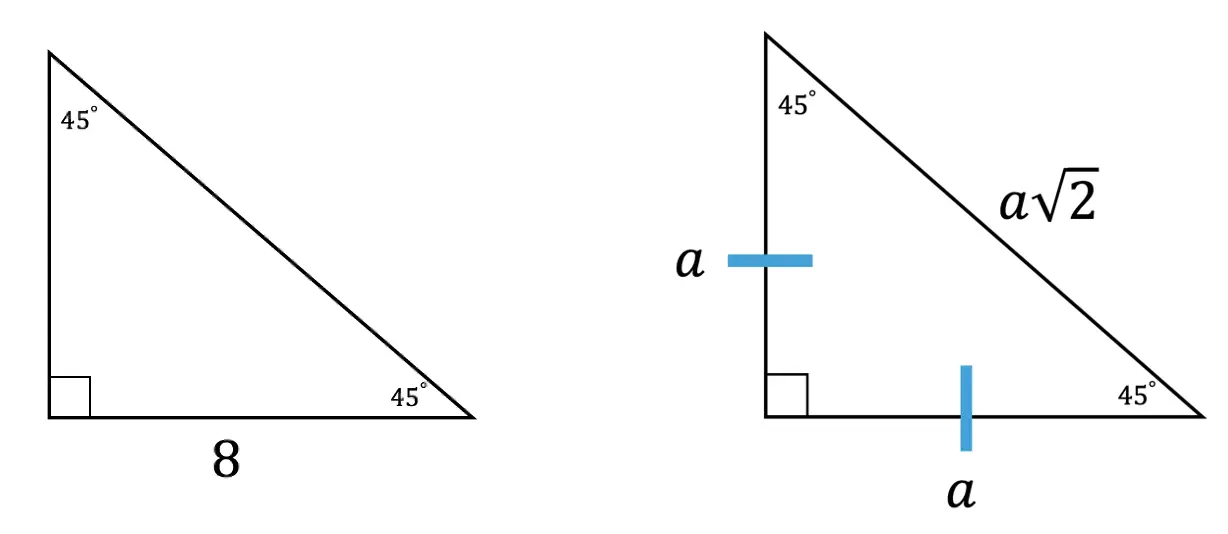
Step 2: Notice we are given the value of the bottom leg, a=8. Knowing this we can fill in each length of our right triangle based on the ratio of a 45 45 90 special triangle shown below:
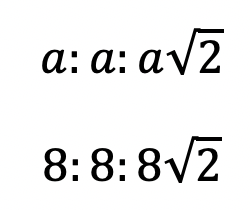
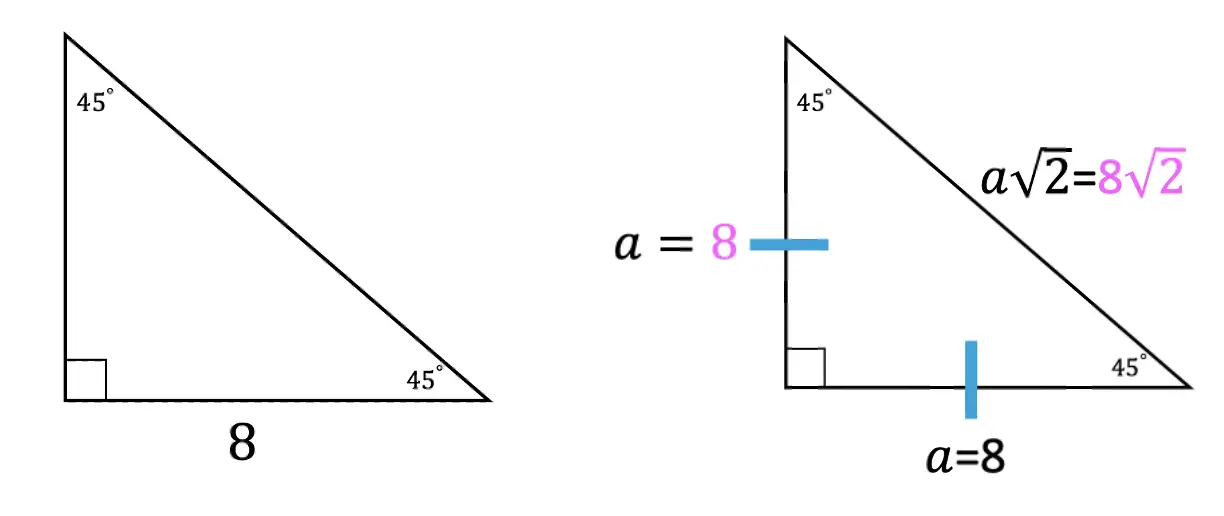
Now let’s look at an example where we are given the length of the hypotenuse and need to find the values of the other two missing sides of a 45 45 90 right triangle.
Example #2:
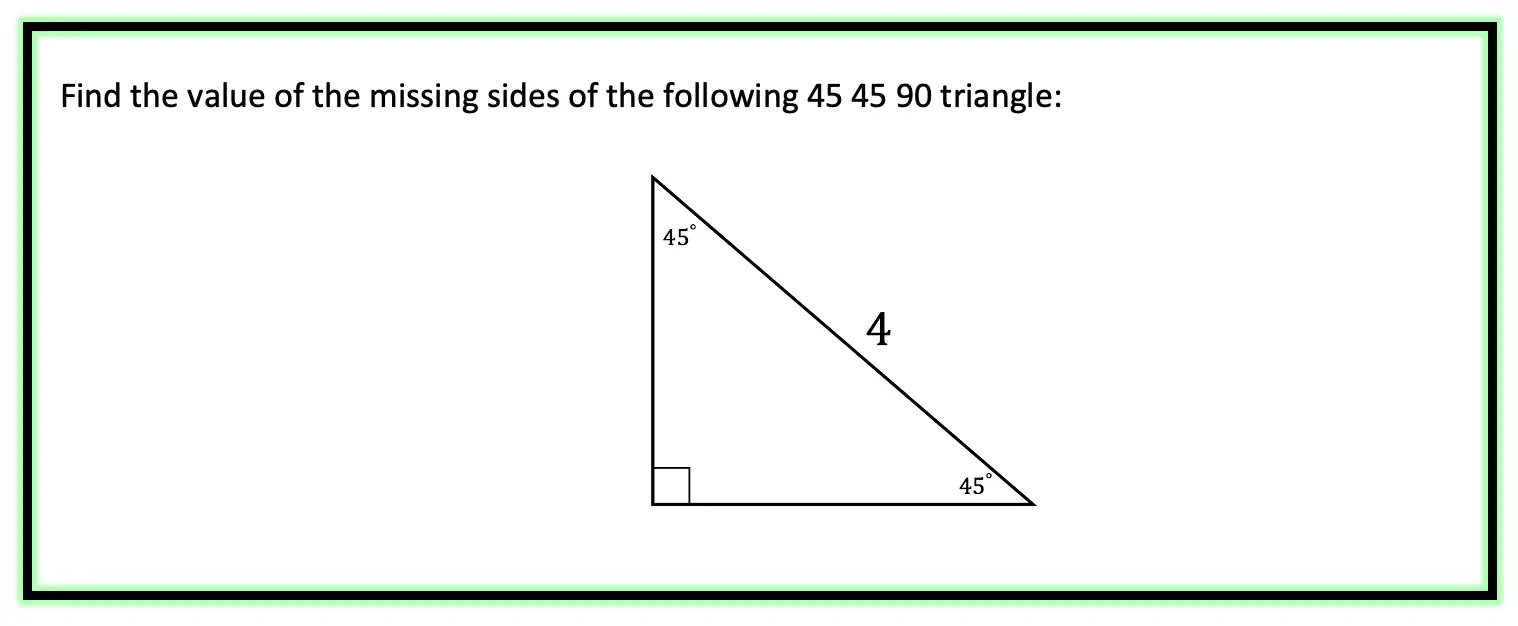
Step 1: First, let’s look at our ratio and compare it to our given right triangle.
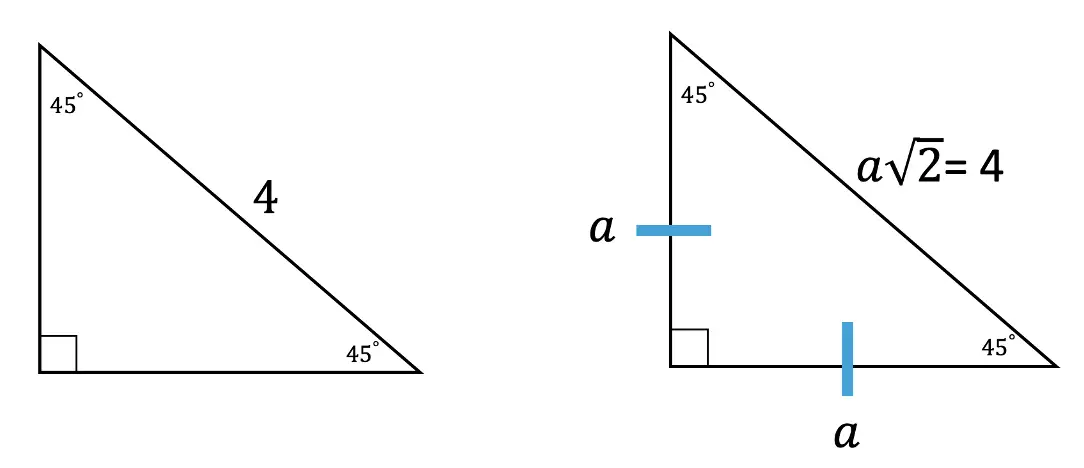
Step 2: In this case, we need to do a little math to find the value of a, based on the Pythagorean Theorem. See how we use the Pythagorean Theorem step by step below to find the value of missing sides represented by a.
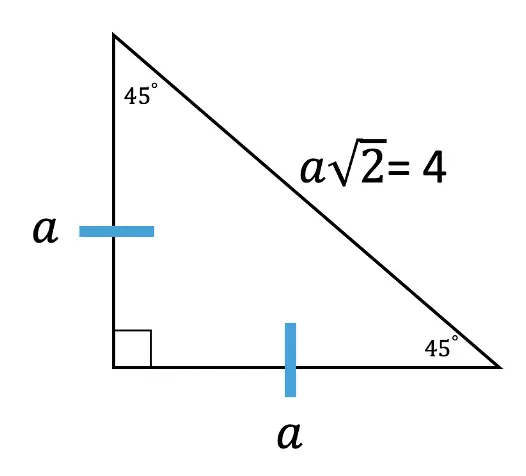

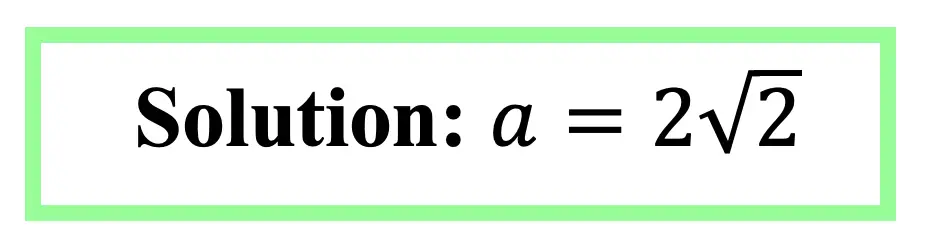
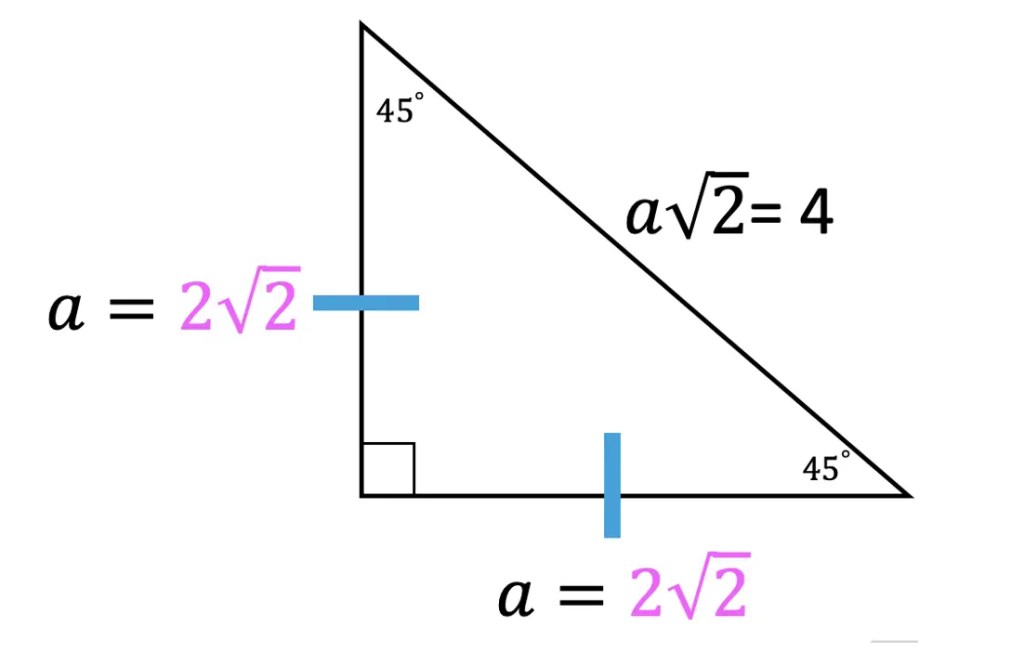
Now try mastering the art of the 45 45 90 special triangle on your own with the practice problems below!
Practice Questions:
Find the value of each missing side length of each 45 45 90 right triangle.
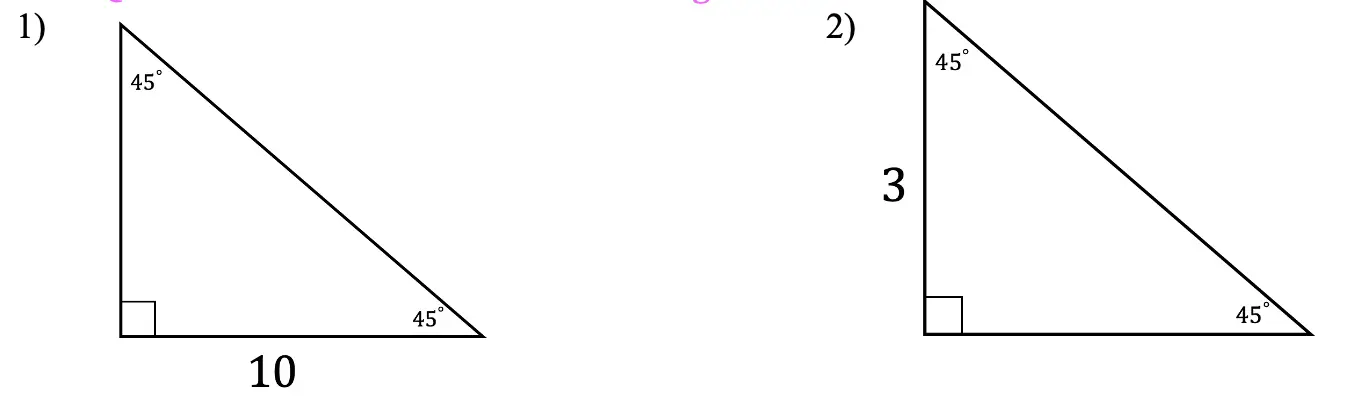
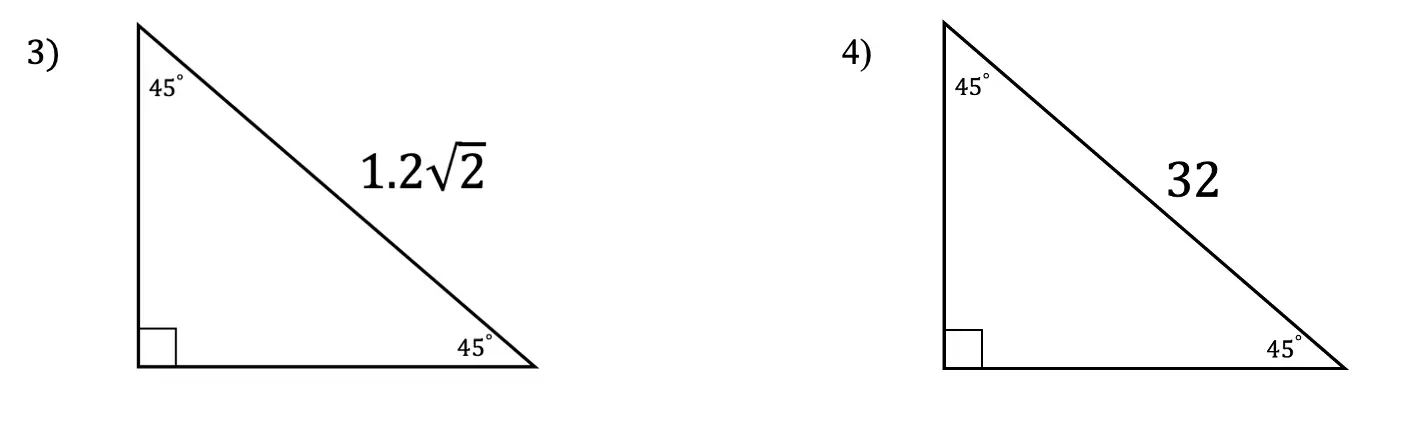
Solutions:
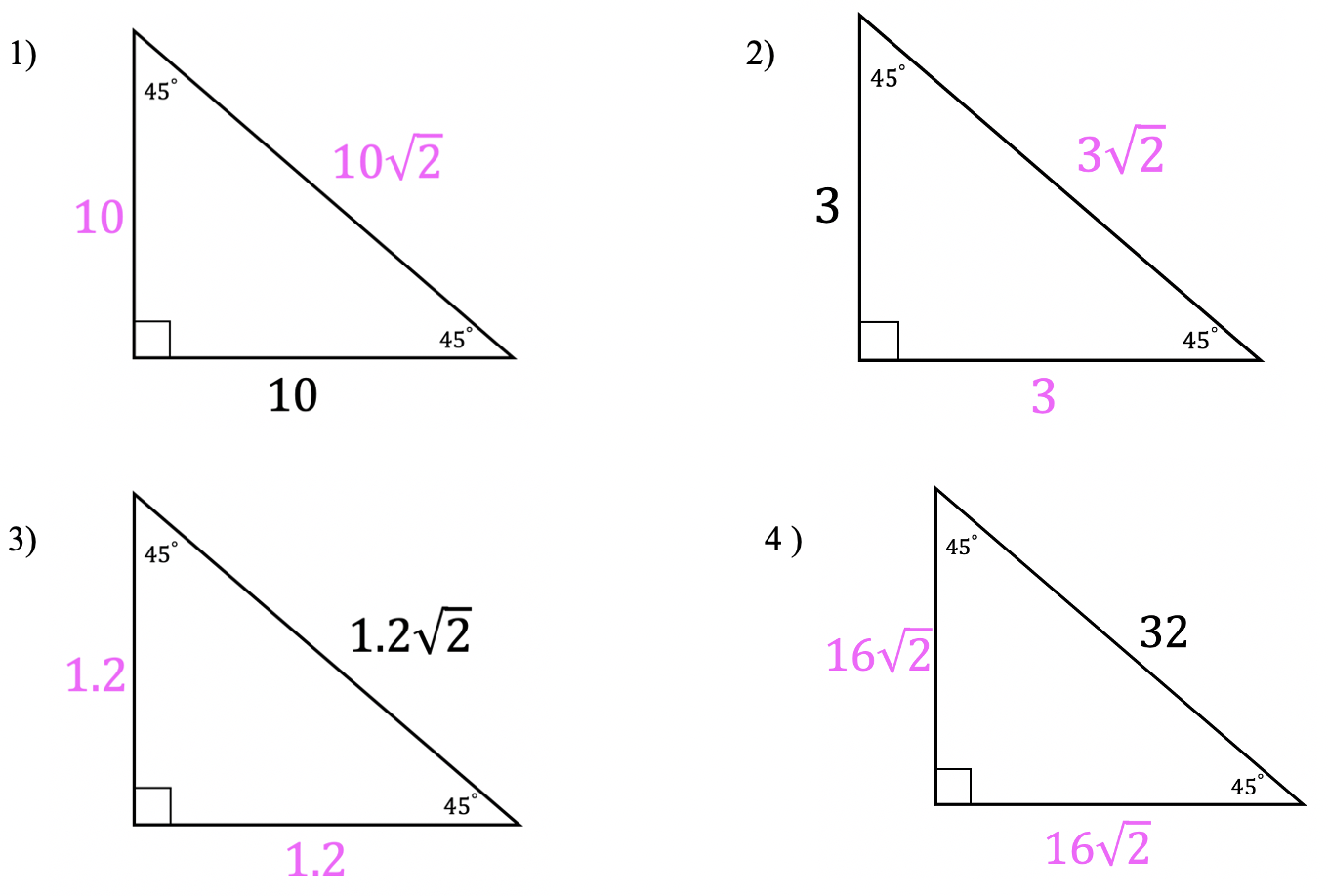
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Related Trigonometry Posts:
Basic Right Triangle Trigonometric Ratios (SOH CAH TOA)
Graphing Trigonometric Functions

6 thoughts on “45 45 90 Triangle”