Geometric Sequence Formula:
an=a1r(n-1)
a1 = First Term
r=Common Ratio (Number Multiplied/Divided by each successive term in sequence)
n= Term Number in Sequence
Hi everyone and welcome to Mathsux! In this post, we are going to answer the question, what is a geometric sequence (otherwise known as a geometric progression)? We will accomplish this by learning how to identify a geometric sequence, then we will break down the geometric sequence formula an=a1r(n-1), and solve two different types of examples. As always if you want more questions, check out the video below and the practice problems at the end of this post. Happy calculating! 🙂
What are Geometric Sequences?
Geometric sequences are a sequence of numbers that form a pattern when the same number is either multiplied or divided to each subsequent term. Take a look at the example of a geometric sequence below:
Example:
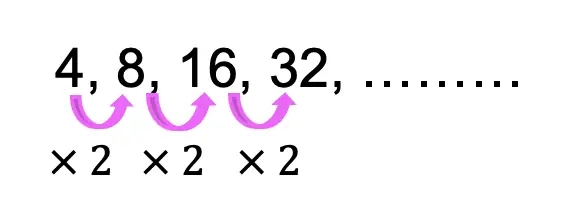
Notice we are multiplying 2 by each term in the sequence above. If the pattern were to continue, the next term of the sequence above would be 64. This is a geometric sequence!
In this geometric sequence, it is easy for us to see what the next term is, but what if we wanted to know the 15th term? Instead of writing out and multiplying our terms 15 times, we can use a shortcut, and that’s where the Geometric Sequence formula comes in handy!
Geometric Sequence Formula:
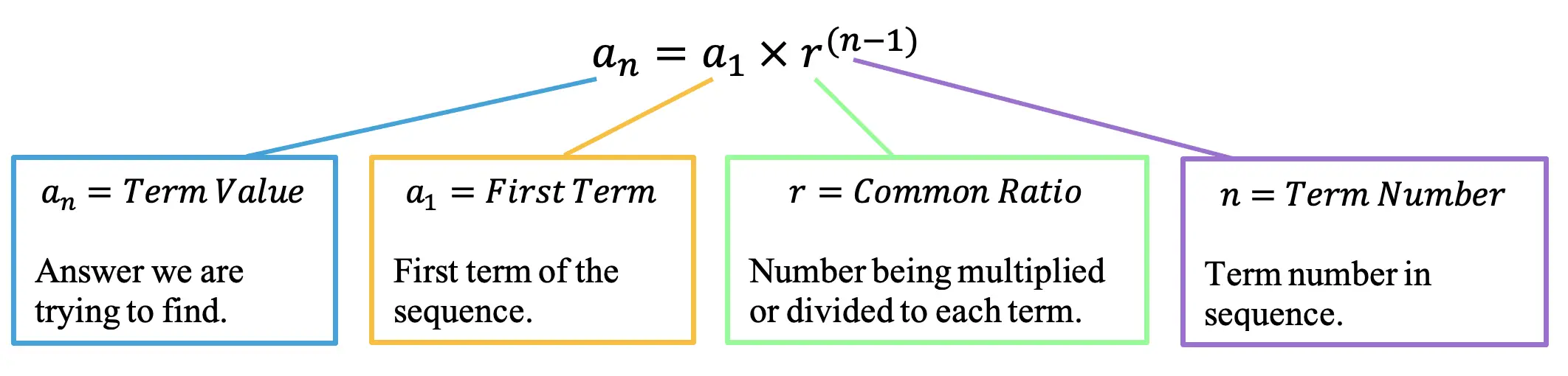
Take a look at the geometric sequence formula below, where each piece of our formula is identified with a purpose.
an=a1r(n-1)
a1 = The first term is always going to be that initial term that starts our geometric sequence. In this case, our sequence is 4,8,16,32, …… so our first term is the number 4.
r= One key thing to notice about the formula below that is unique to geometric sequences is something called the Common Ratio. The common ratio is the number that is multiplied or divided to each consecutive term within the sequence.
n= Another interesting piece of our formula is the letter n, this always stands for the term number we are trying to find. A great way to remember this is by thinking of the term we are trying to find as the nth term, which is unknown.
Now that we broke down our geometric sequence formula, let’s try to answer our original question below:
Example #1: Common ratio r>1

Step 1: First let’s identify the common ratio between each previous and subsequent term of the sequence. Notice each term in the sequence is multiplied by 2 (as we identified earlier in this post). Therefore, our common ratio for this sequence is 2.
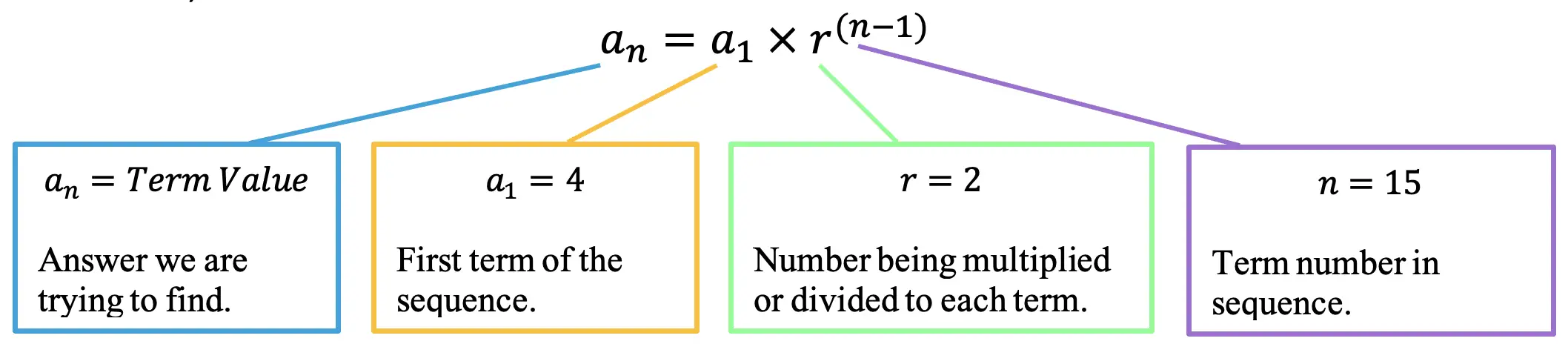
Step 2: Next, let’s write the geometric sequence formula and identify each part of our formula (First Term=4, Term number=15, common ratio=2).
Step 3: Now let’s fill in our formula and solve with the given values.

Let’s look at another example where, the common ratio is a bit different, and instead of multiplying a number, this time we are going to be dividing the same number from each subsequent term, (this can also be thought of as multiplying by a common ratio that is a fraction):
Example #2: Common ratio 0<r<1

Step 1: First let’s identify the common ratio between each number in the sequence. Notice each term in the sequence is divided by 2 (or multiplied by 1/2 that way it is shown below).
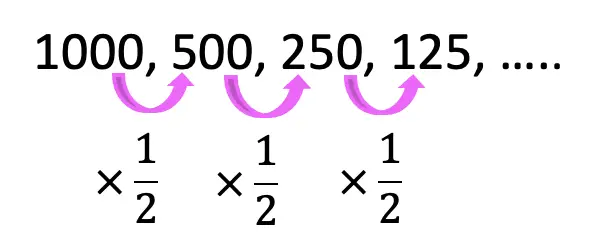
Step 2: Next, let’s write the geometric sequence formula and identify each part of our formula (First Term=1000, Term number=10, common ratio=1/2).
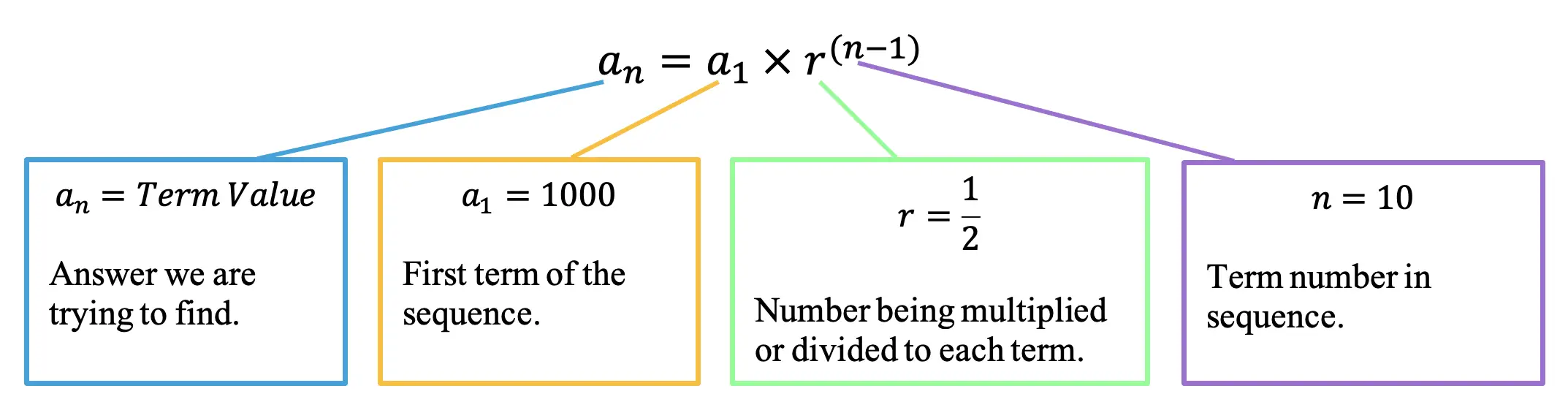
Step 3: Next let’s fill in our formula and solve with the given values.
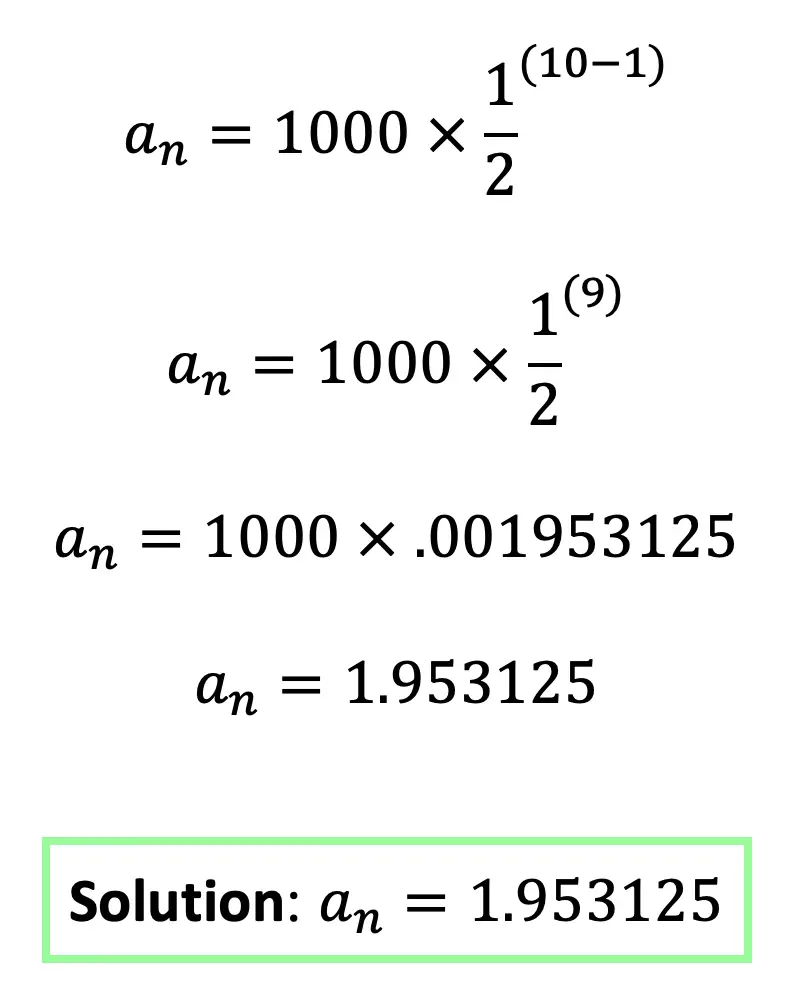
Think you are ready to practice solving geometric sequences on your own? Try the following practice questions with solutions below:
Practice Questions:
- Find the 12th term given the following sequence: 1250, 625, 312.5, 156.25, 78.125, ….
- Find the 17th term given the following sequence: 3, 9, 27, 81, 243,…..
- Find the 10th term given the geometric sequence: 5000, 1250, 312.5, 78.125 …..
- Shirley has $100 that she deposits in the bank. She continues to deposit twice the amount of money every month. How much money will she deposit in the twelfth month at the end of the year?
Solutions:
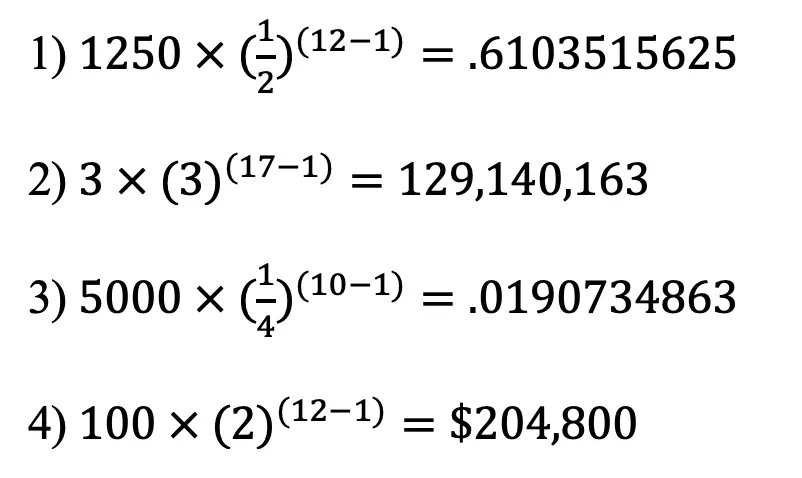
Fun Fact!
Did you know that the geometric sequence formula can be considered an explicit formula? An explicit formula means that even though we do not know the other terms of a sequence, we can still find the unknown value of any term within the given sequence. For example, in the first example we did in this post (example #1), we wanted to find the value of the 15th term of the sequence. We were able to do this by using the explicit geometric sequence formula, and most importantly, we were able to do this without finding the first 14 previous terms one by one…life is so much easier when there is an explicit geometric sequence formula in your life!
Other examples of explicit formulas can be found within the arithmetic sequence formula and the harmonic series.
Related Posts:
Looking to learn more about sequences? You’ve come to the right place! Check out these sequence resources and posts below. Personally, I recommend looking at the finite geometric sequence or infinite geometric series posts next!
Golden Ratio in the Real World
Still, got questions? No problem! Don’t hesitate to comment below or reach out via email. And if you would like to see more MathSux content, please help support us by following ad subscribing to one of our platforms. Thanks so much for stopping by and happy calculating!
Facebook ~ Twitter ~ TikTok ~ Youtube
