Hey math friends! In today’s post, we are going to go over the Intersecting Secants Theorem, specifically using it to find the piece of a missing length on a secant line. We are also going to see proof as to why this theorem works in the first place!
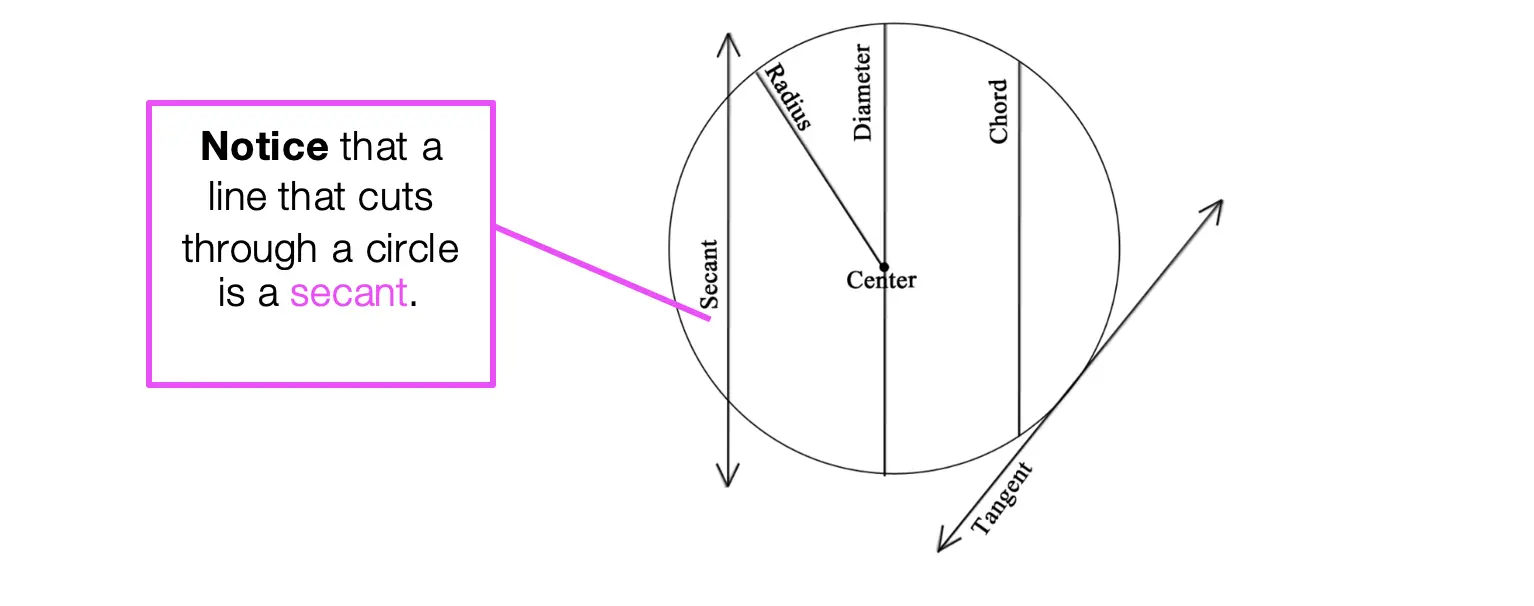
Just a warning: this blog post contains circles. This usually non-threatening shape can get intimidating when secants, chords, and tangents are involved. Luckily, this question is not too complicated and was also spotted on the NYS Regents. Before looking at the questions below, here is a review on different parts of a circle. Pay close attention to what a secant is, which is what we’ll be focusing on today:
Think you are ready? Let’s look at that next question!
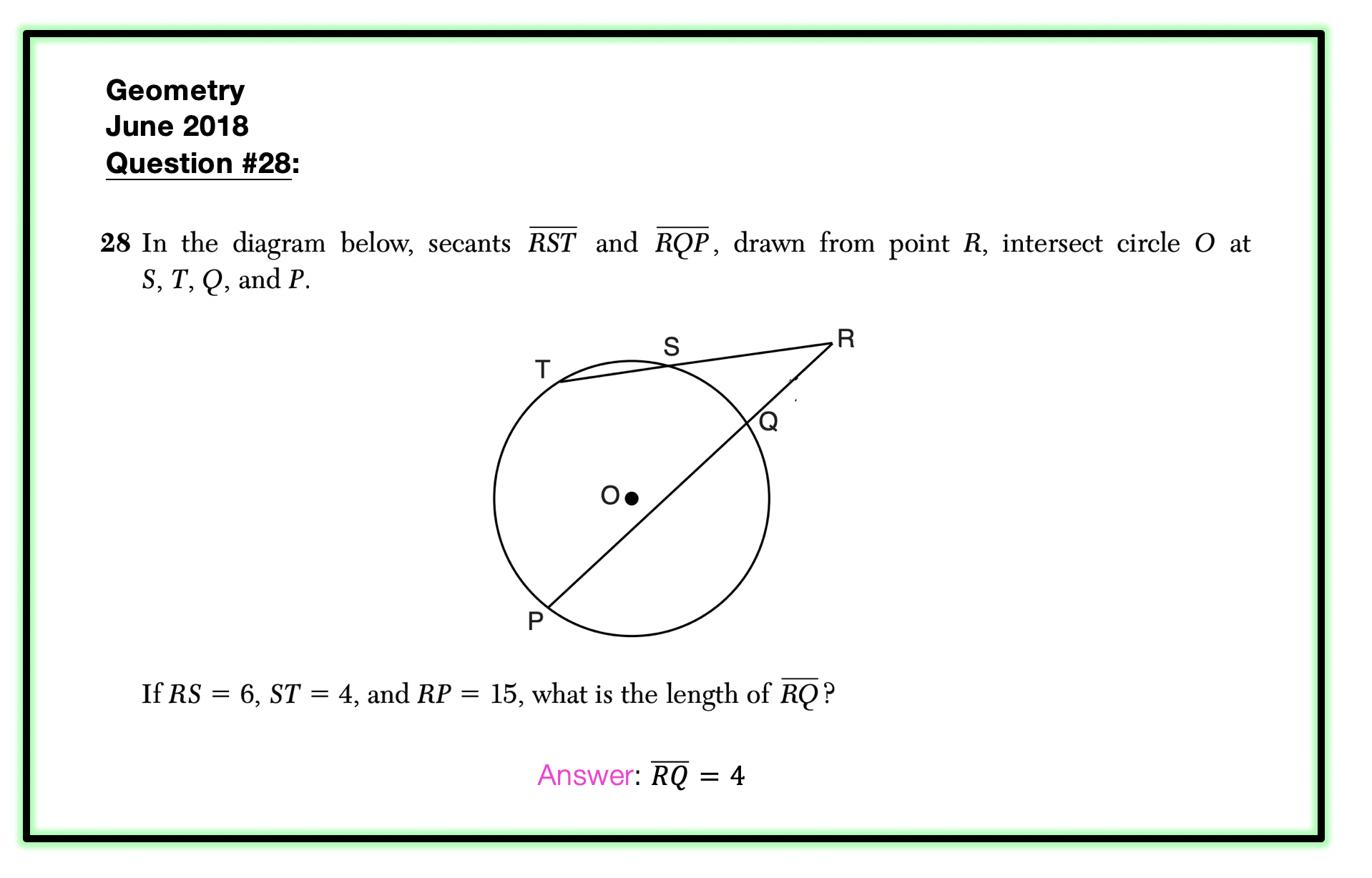
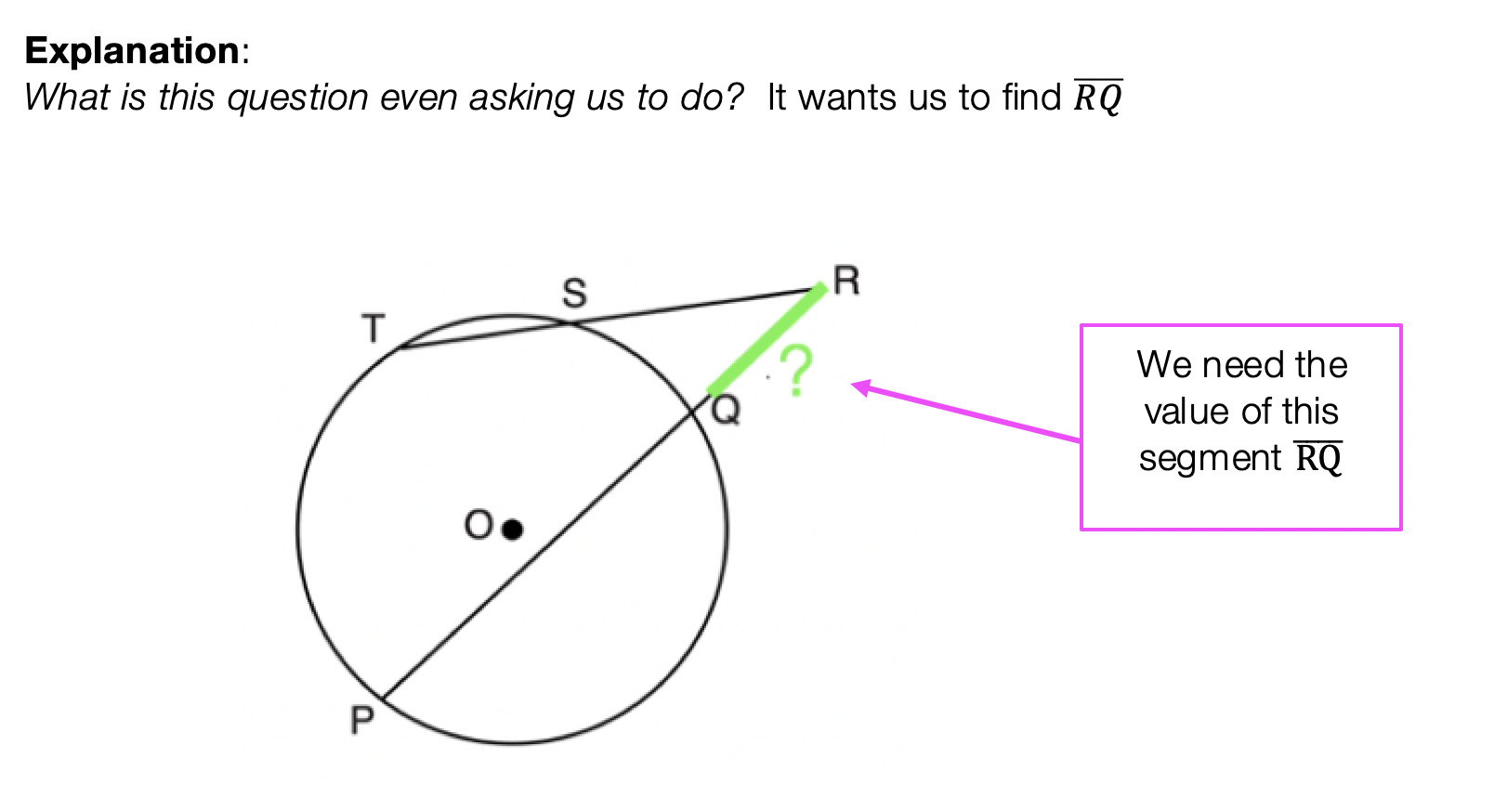
What information do we already have? Based on the question we know:
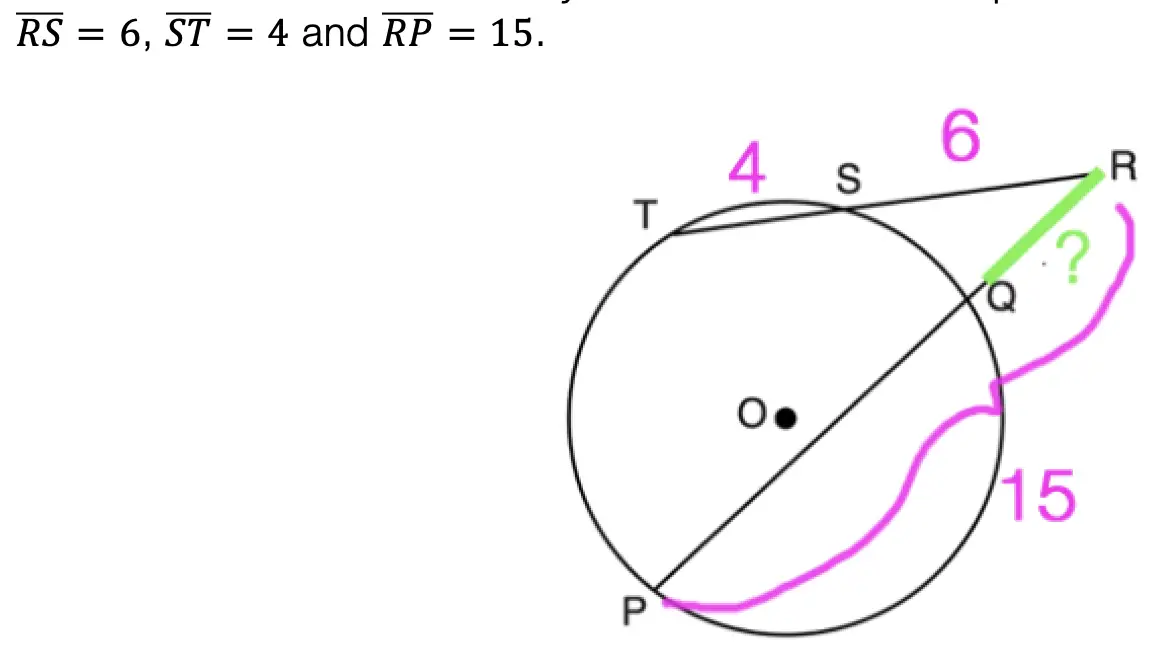
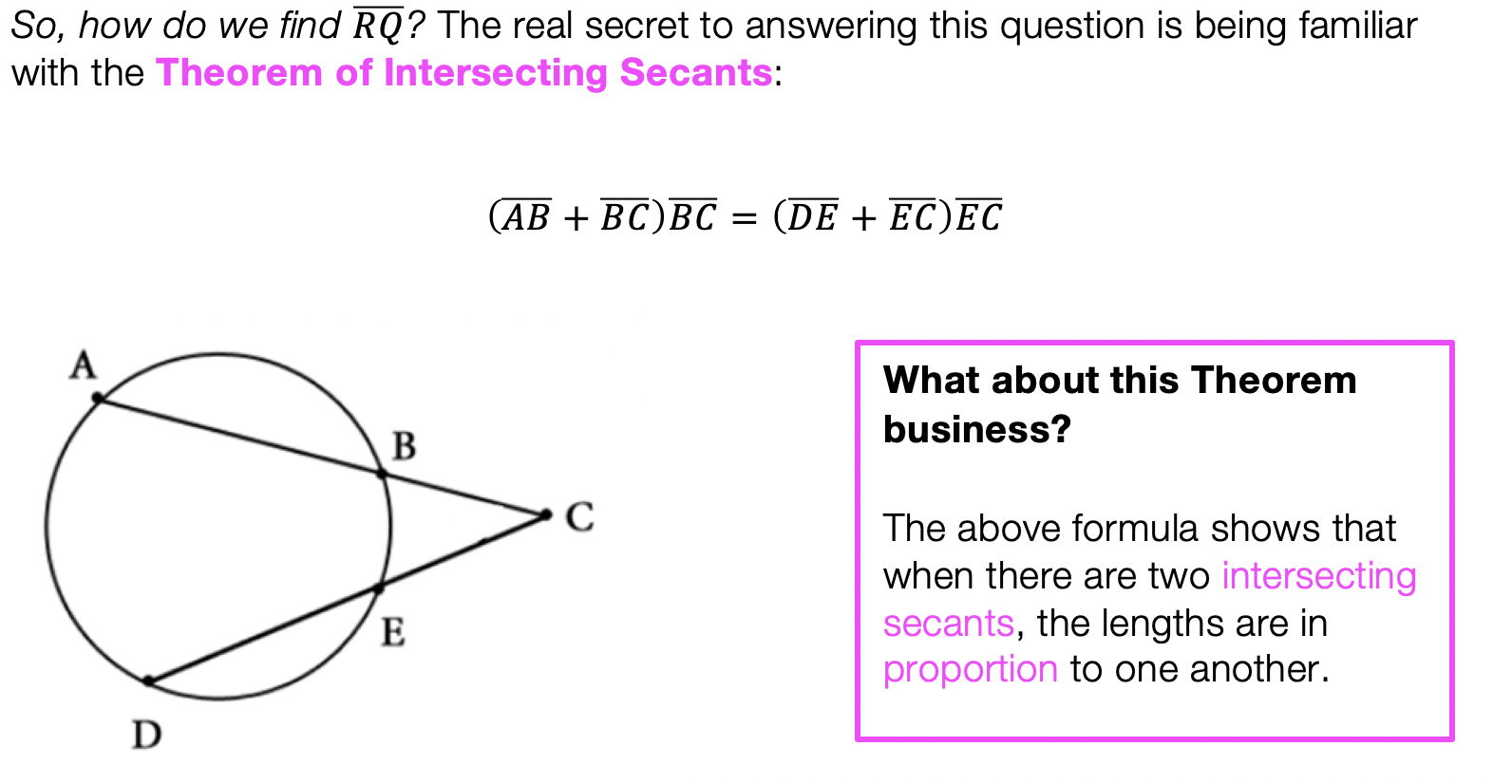
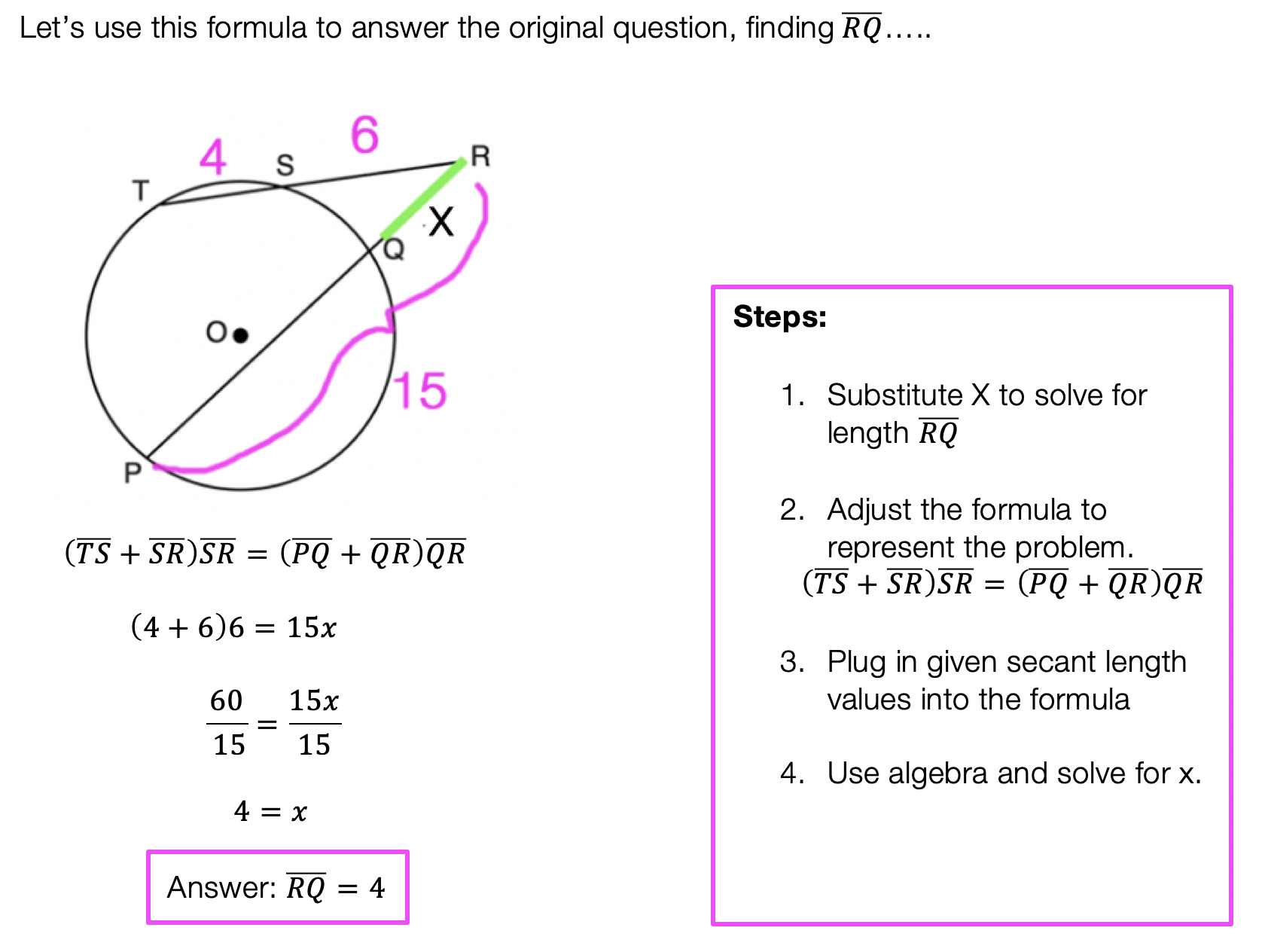
*Extra Tip! Why does this formula work in the first place!?? If we draw lines creating and proving triangle RTQ and triangle RPS are similar by AA, this leads us to know that the two triangles have proportionate sides and can follow our formula! ___________________________________________________________________________________
Still got questions? Let me know in the comments and remember having questions is a good thing!
If you’re looking for more on intersecting secants, check out this post here for practice questions and more!

One thought on “Intersecting Secants: Geometry”