an=a1+(n-1)d
a1=First Term
n=Term Number in Sequence
d=Common Difference (Number Added/Subtracted to each Term in Sequence)
Hi everyone and welcome to Mathsux! In this post, we’re going to go over arithmetic sequences (otherwise known as arithmetic progression). We’ll identify what arithmetic sequences are, break down each part of the arithmetic sequence formula an=a1+(n-1)d, and solve two different types of examples. As always if you want more questions, check out the video below and the practice problems at the end of this post. Happy calculating! 🙂
What are Arithmetic Sequences?
Arithmetic sequences are a sequence of numbers that form a pattern when the same number is either added or subtracted to each successive term. Take a look at the example of an arithmetic sequence below:
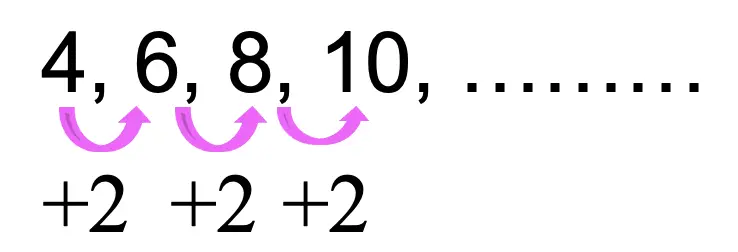
Notice the pattern? We are adding the number 2 to each term in the sequence above. If the pattern were to continue, the next term of the sequence above would be 10+2 which gives us 12. This is an arithmetic sequence!
In the above sequence, it’s easy for us to identify what the next term in the sequence would be, but what happens if we were asked to find the 123rd term of an arithmetic sequence? That’s where the Arithmetic Sequence Formula would come in handy!
Arithmetic Sequence Formula:
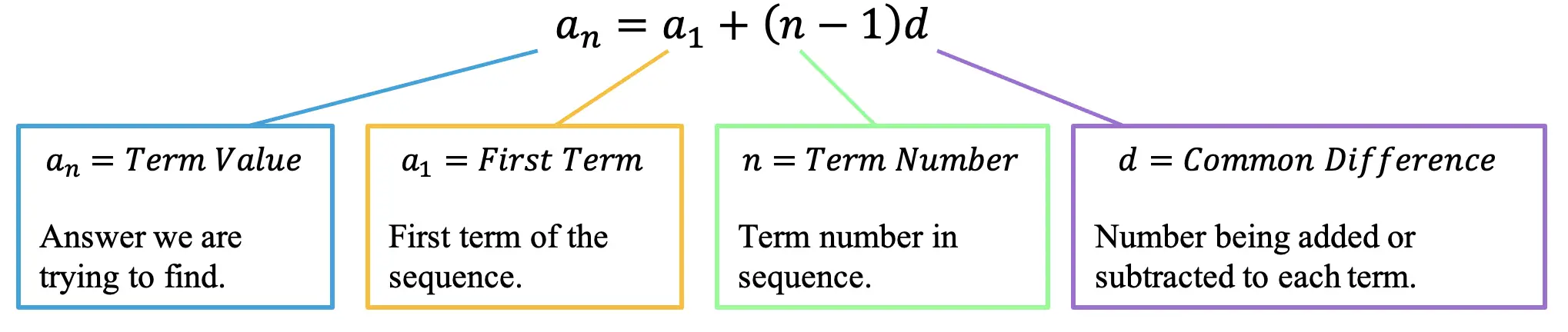
Take a look at the arithmetic sequence formula below, where each piece of our formula is identified with a purpose.
an=a1+(n-1)d
a1= The first term is always going to be that initial term that starts our arithmetic sequence. In this case, our sequence is 4,6,8,10, …… so our first term is the number 4.
n= Another interesting piece of our formula is the letter n, this always stands for the term number we are trying to find. A great way to remember this is by thinking of the term we are trying to find as the nth term, which is unknown.
d = One key thing to notice about the formula below that is unique to arithmetic sequences is something called the Common Difference. The common difference is the number that is added or subtracted to each consecutive term within the sequence.
Now that we know the arithmetic sequence formula, let’s try to answer our original question below:

Step 1: First let’s identify the common difference between each previous and subsequent term of the sequence. Notice each term in the sequence is being added by 2 (like we identified earlier in this post). Therefore, our common difference for this sequence is 2.
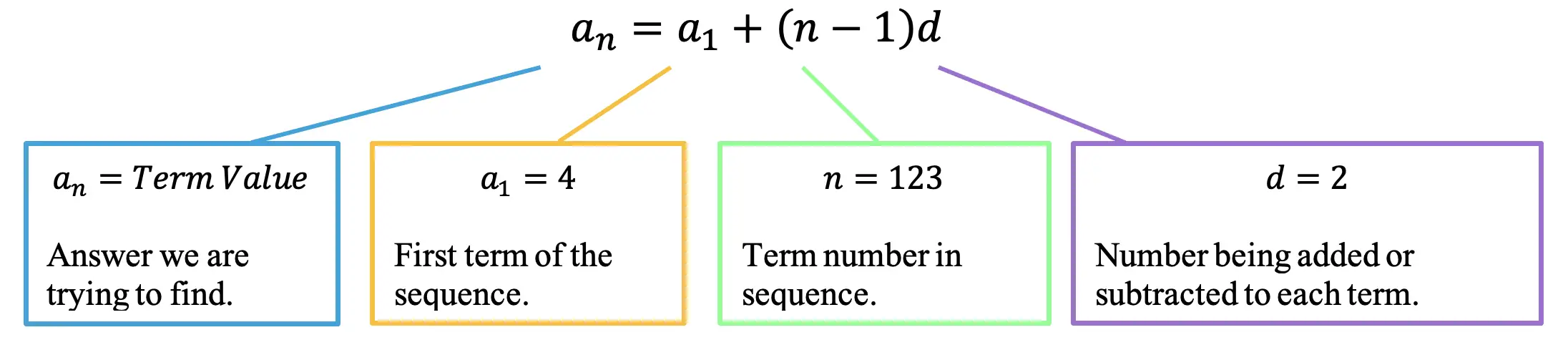
Step 2: Next, let’s write the arithmetic sequence formula and identify each part of our formula (First Term=4, Term number=123, common difference=2).
Step 3: Fill in our formula and solve with the given values.

Now let’s look at another example where we subtract the same number from each term in the sequence, making the common difference negative.

Step 1: First let’s identify the common difference between each previous term and each subsequent term of the sequence. Notice each term in the sequence is being subtracted by 3. Therefore, our common difference for this sequence is -3, negative, because we are subtracting.
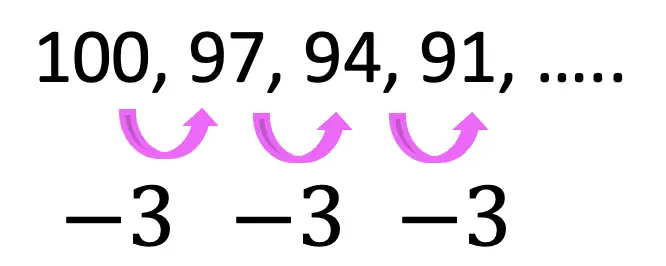
Step 2: Next, let’s write the arithmetic sequence formula and identify each part of our formula (First Term=100, Term number=12, common difference=-3).
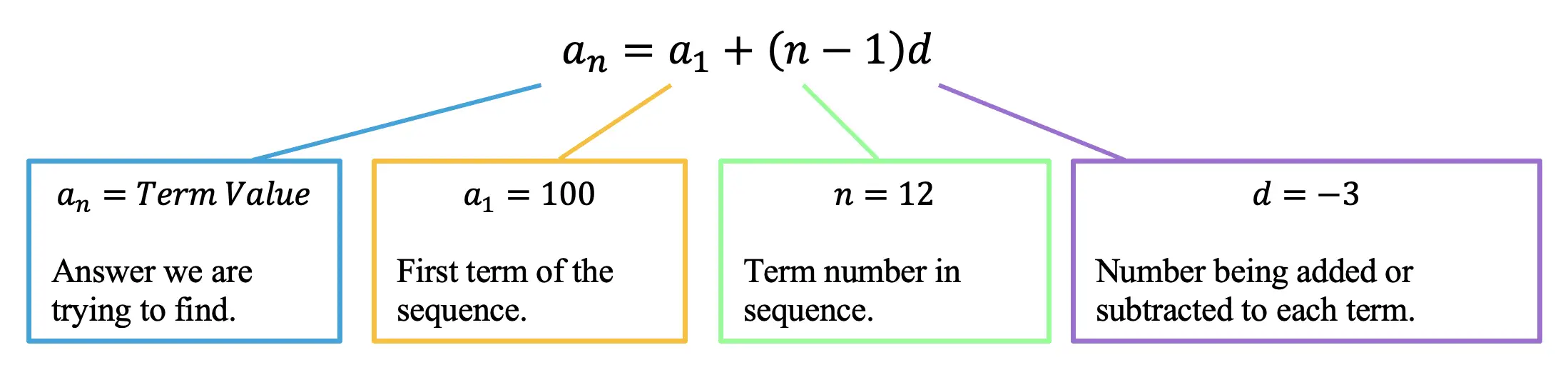
Step 3: Finally, let’s fill in our formula and solve with the given values.

Think you are ready to practice solving arithmetic sequences on your own? Try the following practice questions with solutions below:
Practice Questions:
- Find the 123rd term given the following sequence: 8, 12, 16, 20, 24, ….
- Find the 117th term given the following sequence: 2, 2.5, 3, 3.5, …..
- Find the 52nd term given arithmetic sequence: 302, 300, 298, …..
- A software engineer charges $100 for the first hour of consulting and $50 for each additional hour. How much would 500 hours of the consultation cost?
Solutions:
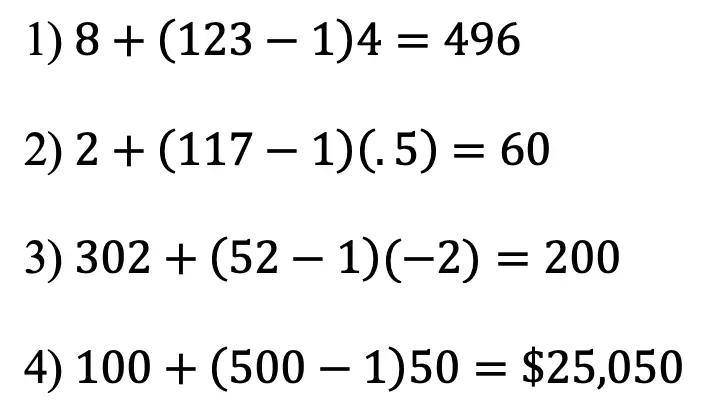
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂
Fun Fact!
Did you know that the arithmetic sequence formula can be considered an explicit formula? An explicit formula means that even though we do not know the other terms of a sequence, we can still find the unknown value of any term within the given sequence. For example, in the first example we did in this post (example #1), we wanted to find the value of the 123rd term of the sequence. We were able to do this by using the explicit arithmetic sequence formula, and most importantly, we were able to do this without finding the first 122 previous terms one by one…life is so much easier when there is an explicit arithmetic sequence formula in your life!
Other examples of explicit formulas can be found within the geometric sequence formula and the harmonic series.
Related Posts:
Looking to learn more about sequences? You’ve come to the right place! Check out these sequence resources and posts below. Personally, I recommend looking at the geometric sequence or finite arithmetic series posts next!
Golden Ratio in the Real World
Still, got questions? No problem! Don’t hesitate to comment below or reach out via email. And if you would like to see more MathSux content, please help support us by following ad subscribing to one of our platforms. Thanks so much for stopping by and happy calculating!

10 thoughts on “Arithmetic Sequence Formula:”