Welcome to Mathsux! This post is going to show you everything you need to know about how to use a Recursive Formula by looking at three different examples of a recursive rule. Check out the video below for more of an explanation and test your skills with the practice questions at the bottom of this page. Please let me know if you have any questions in the comments section below and happy calculating! 🙂
What is a Recursive Formula or a Recursive Rule?
A Recursive Formula is a type of formula that forms a sequence based on the previous term value. The recursive rules for each formula vary, but we are always given the first term and a formula to find the consecutive terms in the recursive sequence.
Recursive formula can be written as an arithmetic sequence (a sequence where the same number is either added or subtracted to each subsequent term to form a pattern) and recursive formulas can also be written as arithmetic sequences (a sequence where the same number is either multiplied or divided to each subsequent term to form a pattern). We’ll go over an example of each but both types of recursive rules are treated the same exact way!
What does all of this mean? Check out the example below for a clearer picture.
Example #1: Arithmetic Recursive Sequence
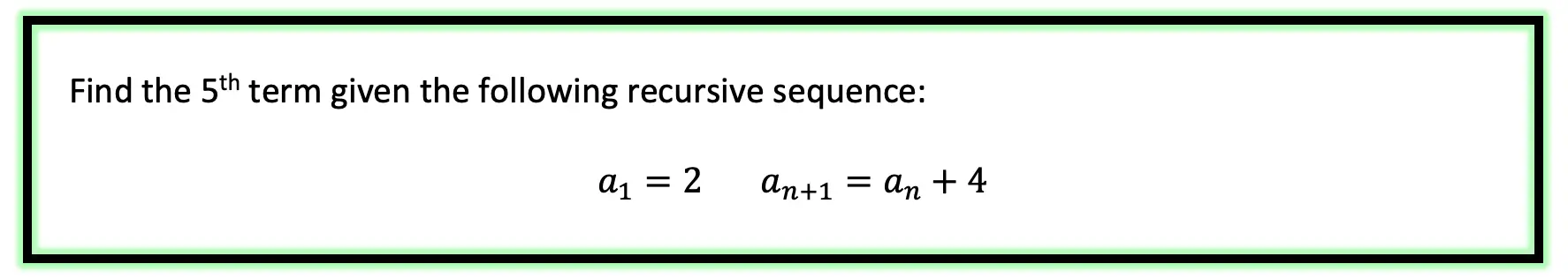
Step 1: First, let’s decode what these formulas are saying.
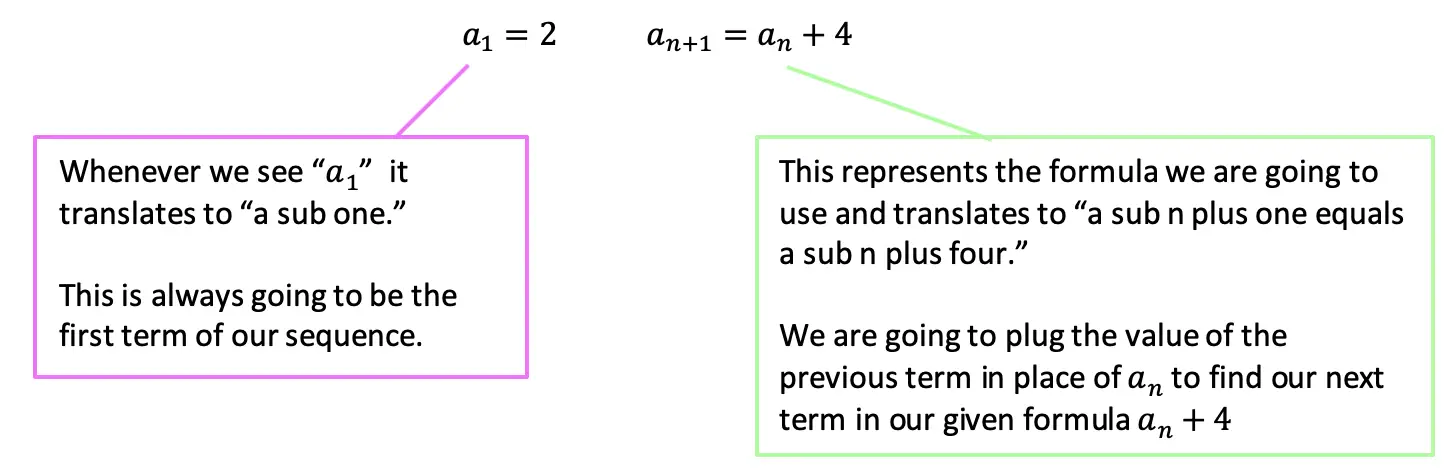
Step 2: The first term, represented by a1, is and will always be given to us. In this case, our first term has the value a1=2 and represents the first term of our recursive sequence.
a1= First Term=2
Step 3: We then plug in the value of our first term, which is a1=2 into our formula an+4 to get 2+4=6. The number 6 now has the value of our second term in the recursive sequence.
a1= 2 First Term
a2= (2)+4=6 Second Term
Step 4: Now we are going to continue the pattern, plugging in the value of each previous term to find the next consecutive terms in our recursive sequence.
The pattern can be more easily seen below. Notice we are able to find the value of all 5 terms of the recursive sequence for the solution only given the first term and recursive formula at the beginning of our question.
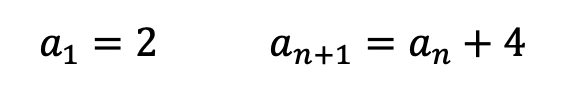

Step 5: We found the recursive sequence we were looking for: 2, 6, 10, 14, 18. Since the question was originally only asking for the value of the fifth term we know our solution only needs to be the value of the fifth term which is 18.

Example #2: Geometric Recursive Sequence
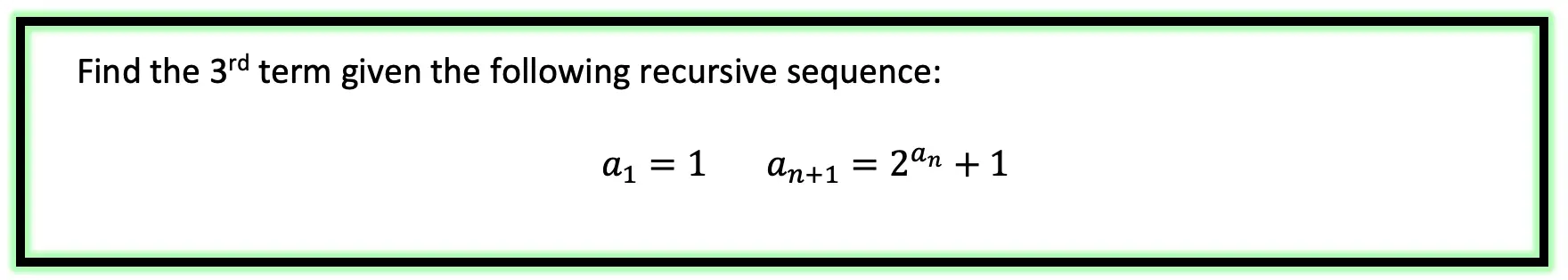
Step 1: First, let’s decode what these formulas are saying.
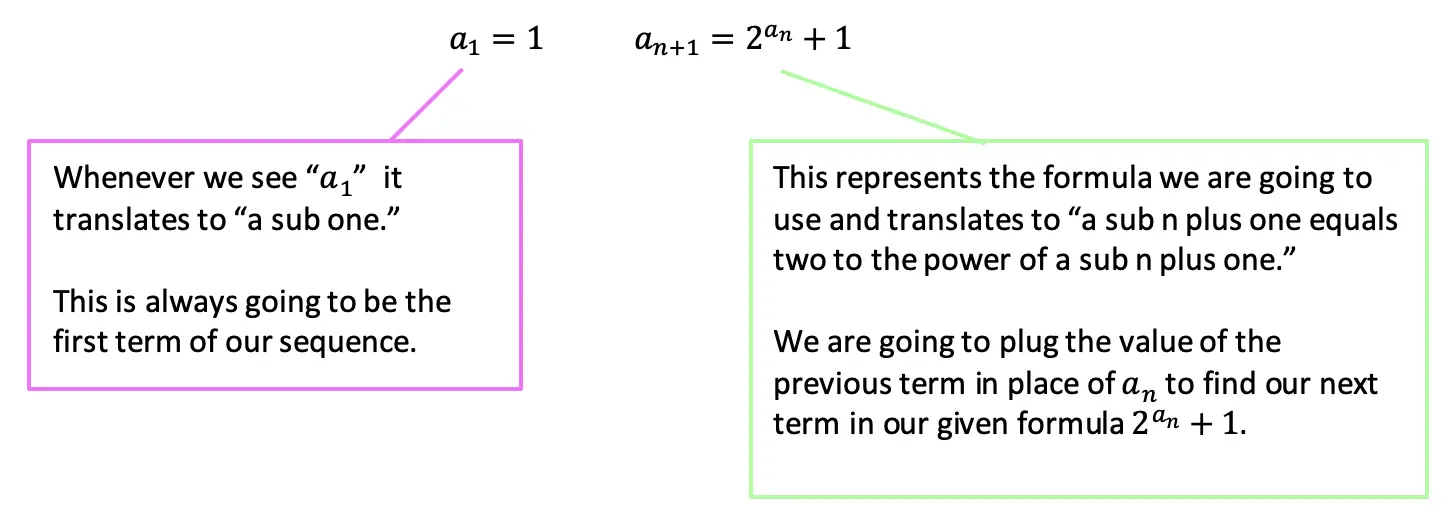
Step 2: The first term, represented by a1, is and will always be given to us. In this case, our first term has the value a1=1 and represents the first term of our recursive sequence.
a1= First Term=1
Step 3: We then plug in the value of our first term, which is a1=1 into our formula 2an+1 to get 21+1=3. The number 3 now has the value of our second term in the recursive sequence.
a1= 1 First Term
a2= 2(1)+1=3 Second Term
Step 4: Now we are going to continue the pattern, plugging in the value of each previous term to find the next term in our recursive sequence.
The pattern can be more easily seen below. Notice we are able to find the value of all 3 terms of the recursive sequence for the solution only given the first term and recursive formula at the beginning of our question.
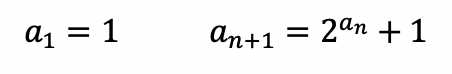

***Note this was written in a different notation but is solved in the exact same way! This recursive formula is a geometric sequence.
Step 5: We found the recursive sequence we were looking for: 1,3,9. Since the question was originally only asking for the value of the third term we know our solution only needs to be the value of the third term which is 9.

Example #3:
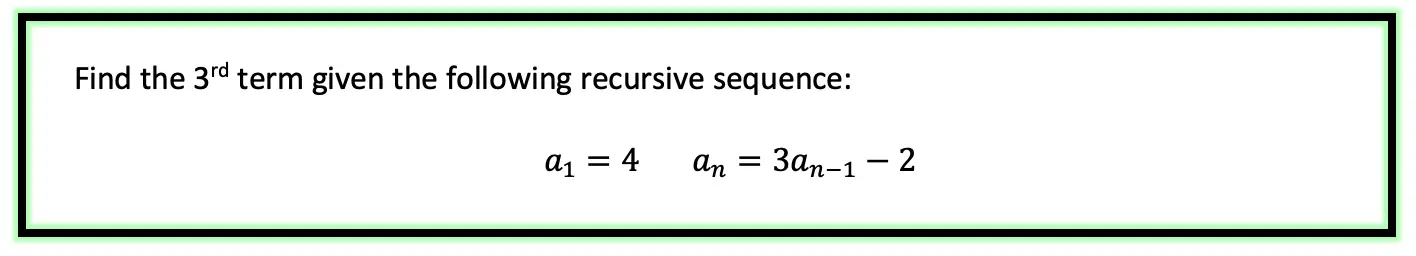
Step 1: First, let’s decode what these formulas are saying.

Step 2: The first term, represented by a1, is and will always be given to us. In this case, our first term has the value a1=4 and represents the first term of our recursive sequence.
a1= First Term=4
Step 3: We then plug in the value of our first term, which is a1=4 into our formula 3an-1-2 to get 3(2)-1=5. The number 5 now has the value of our second term in the recursive sequence.
a1= 4 First Term
a2= 3(2)-1=5 Second Term
Step 4: Now we are going to continue the pattern, plugging in the value of each previous term to find the next term in our recursive sequence.
The pattern can be more easily seen below. Notice we are able to find the value of all 3 terms of the recursive sequence for the solution only given the first term and recursive formula at the beginning of our question.

Step 5: We found the recursive sequence we were looking for: 4,10,28. Since the question was originally only asking for the value of the third term we know our solution only needs to be the value of the third term which is 28.

Think you are ready to solve a recursive equation on your own?! Try finding the specific term in each given recursive function below:
Practice Questions:

Solutions:
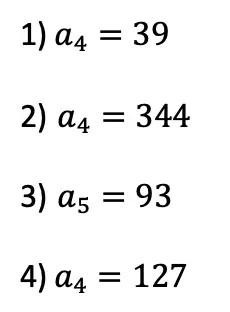
Related Posts:
Looking to learn more about sequences? You’ve come to the right place! Check out these sequence resources and posts below. Personally, I recommend looking at the arithmetic sequence or geometric sequence posts next!
Golden Ratio in the Real World
Still, got questions? No problem! Don’t hesitate to comment below or reach out via email. And if you would like to see more MathSux content, please help support us by following ad subscribing to one of our platforms. Thanks so much for stopping by and happy calculating!
Facebook ~ Twitter ~ TikTok ~ Youtube
***Bonus! Want to test yourself with a similar NYS Regents question on Recursive Formulas? Click here! And if you want to learn about even more sequences, check out the link here!

3 thoughts on “Recursive Rule”