Happy Wednesday math friends! Today, we’re going to go over how to solve absolute value equations. Solving for absolute value equations supplies us with the magic of two potential answers since absolute value is measured by the distance from zero. And if this sounds confusing, fear not, because everything is explained below!
Also, if you have any questions about anything here, don’t hesitate to comment. Happy calculating! 🙂
Absolute Value measures the “absolute value” or absolute distance from zero. For example, the absolute value of 4 is 4 and the absolute value of -4 is also 4. Take a look at the number line below for a clearer picture:
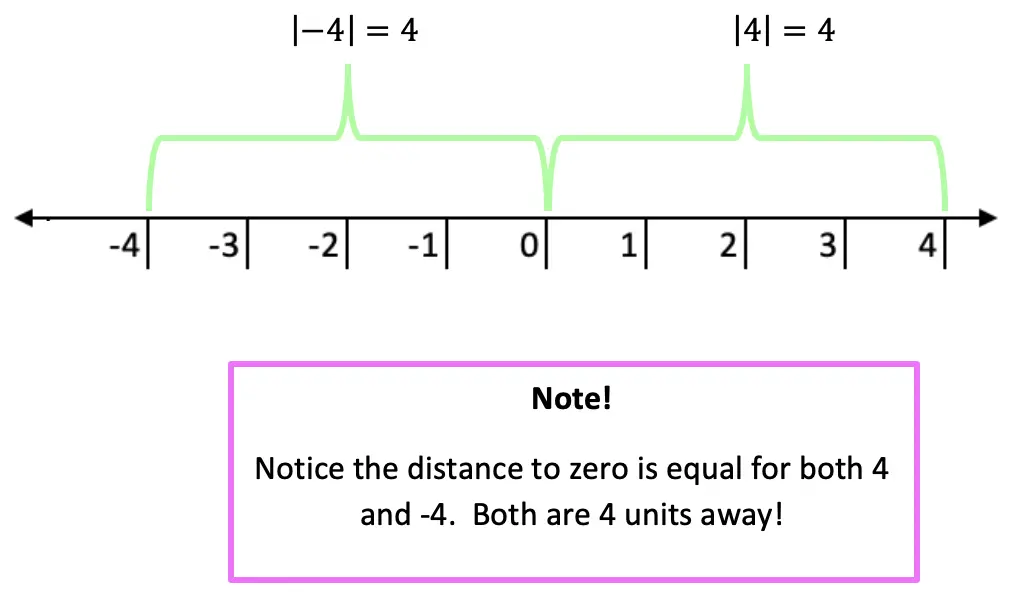
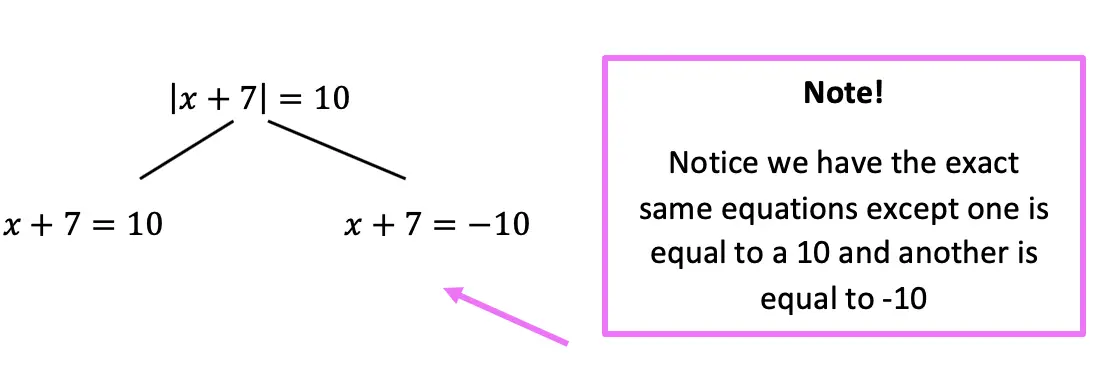
Now let’s see how we can apply our knowledge of absolute value equations when there is a missing variable!
![]()
![]()

![]()
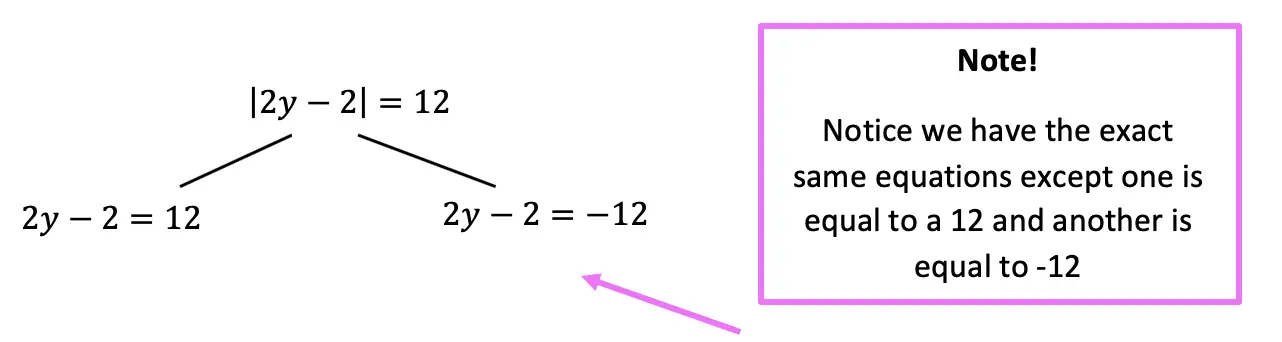
 Now let’s look at a slightly different example:
Now let’s look at a slightly different example:
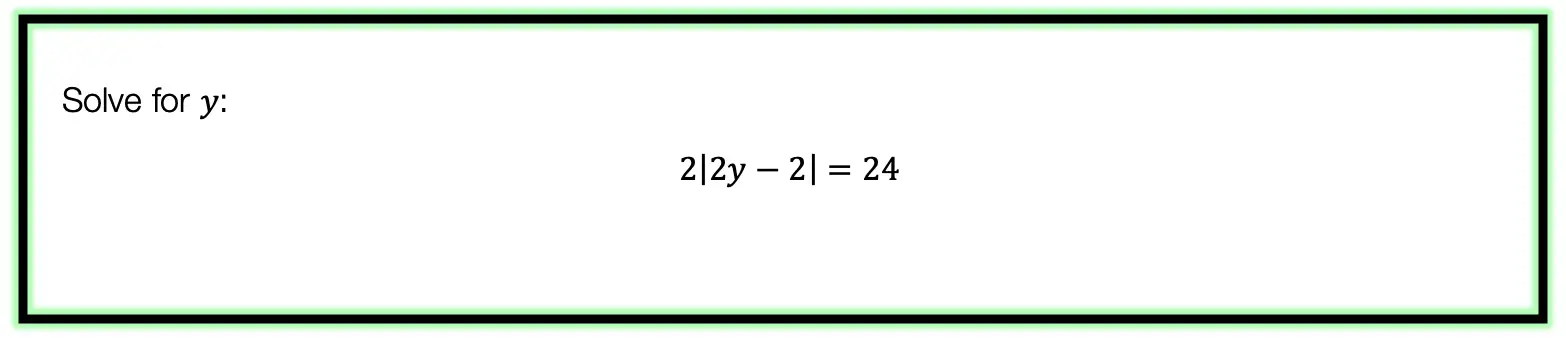


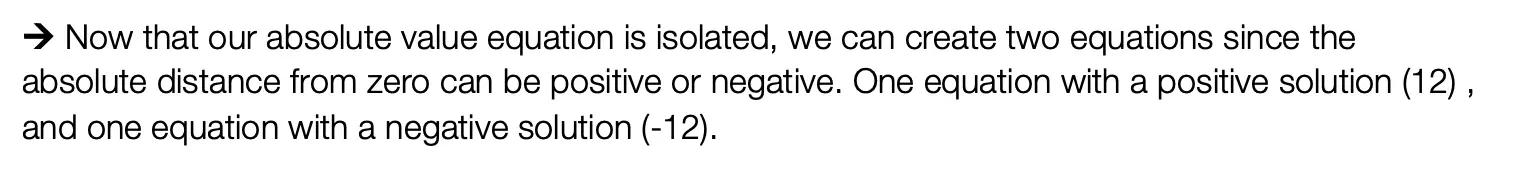
![]()
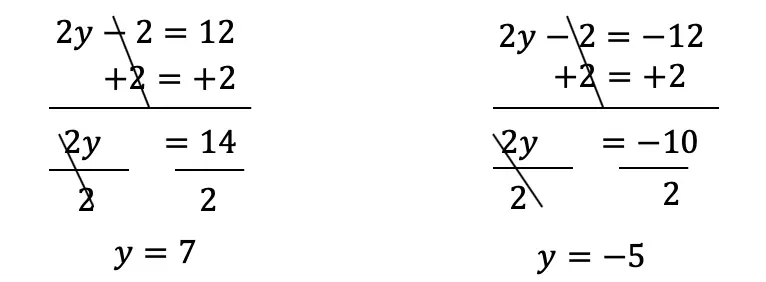
![]()
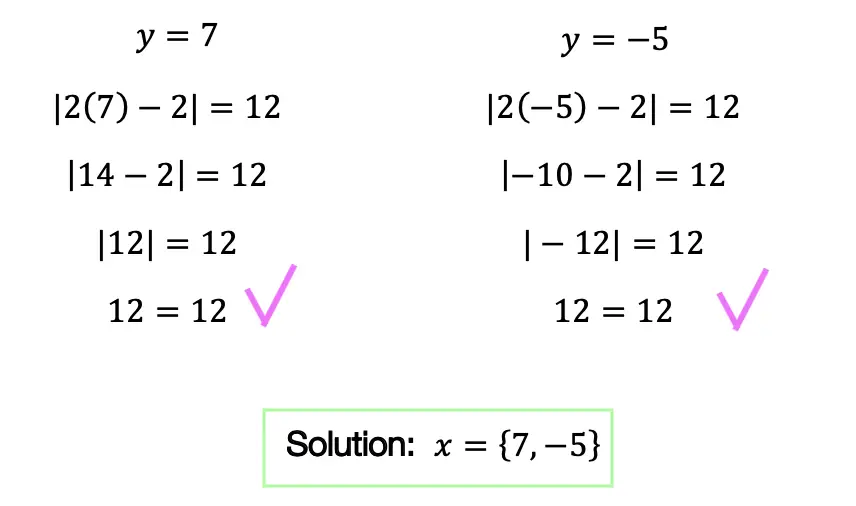
Practice Questions: Given the following right triangles, find the missing lengths and side angles rounding to the nearest whole number.
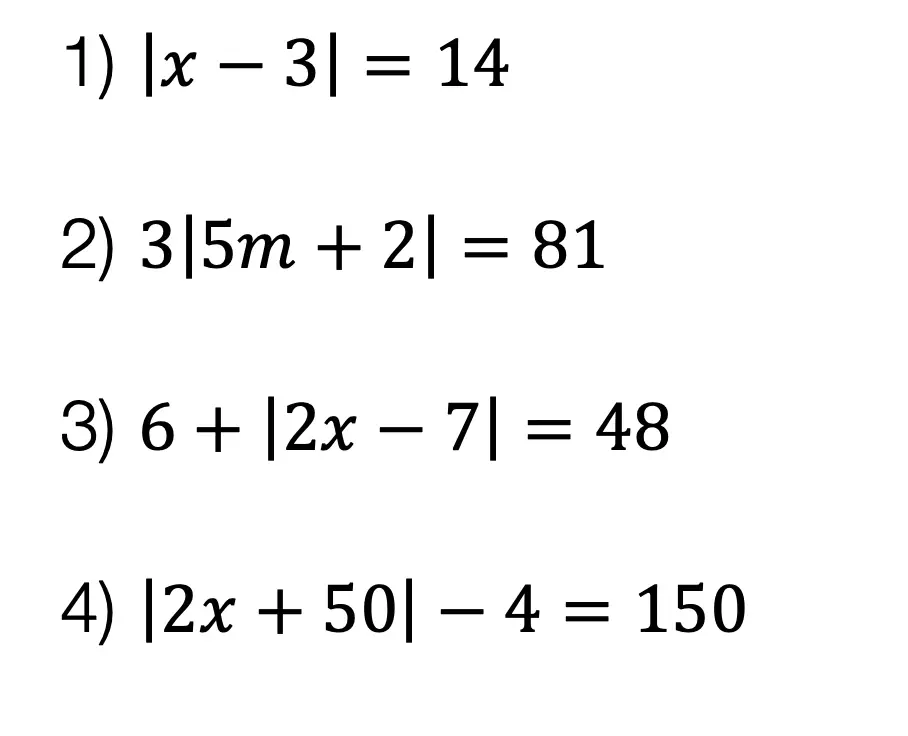
Solutions:
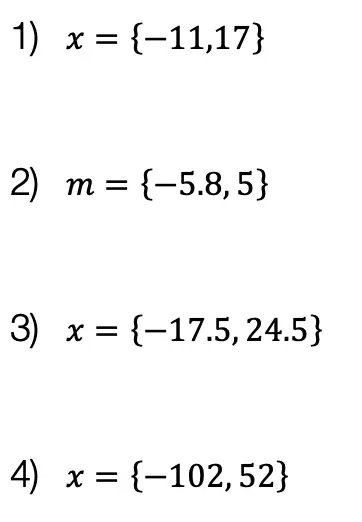
Still got questions? No problem! Check out the video the same examples outlined above. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Also, if you’re looking for a review on combining like terms and the distributive property, check out this post here.

One thought on “Absolute Value Equations: Algebra”