Happy Wednesday math friends! In this post we’re going to dive into rotations about a point! In this post we will be rotating points, segments, and shapes, learn the difference between clockwise and counterclockwise rotations, derive rotation rules, and even use a protractor and ruler to find rotated points. The fun doesn’t end there though, check out the video and practice questions below for even more! And as always happy calculating! 🙂
What are Rotations?
Rotations are a type of transformation in geometry where we take a point, line, or shape and rotate it clockwise or counterclockwise, usually by 90º,180º, 270º, -90º, -180º, or -270º.
A positive degree rotation runs counter clockwise and a negative degree rotation runs clockwise. Let’s take a look at the difference in rotation types below and notice the different directions each rotation goes:
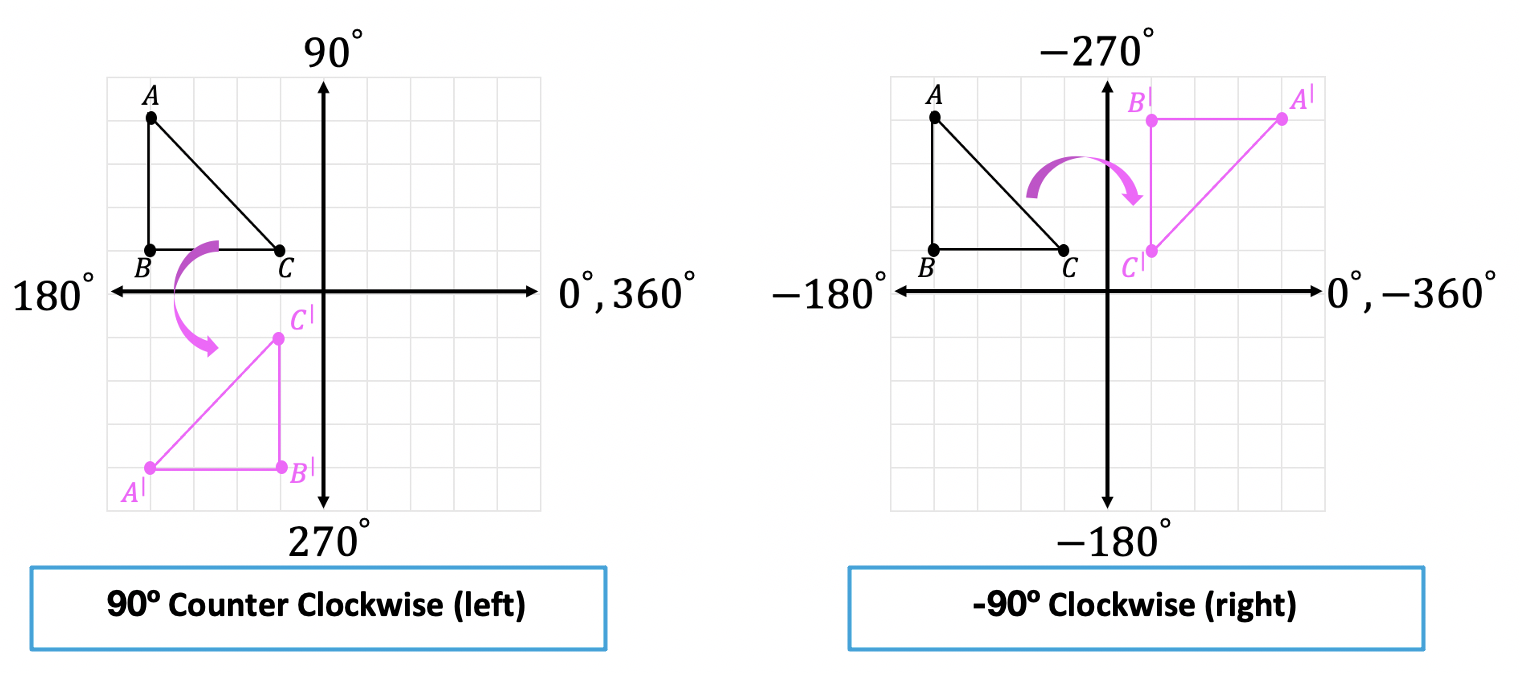
How do we rotate a shape?
There are a couple of ways to do this take a look at our choices below:
- We can visualize the rotation or use tracing paper to map it out and rotate by hand.
- Use a protractor and measure out the needed rotation.
- Know the rotation rules mapped out below. Yes, it’s memorizing but if you need more options check out numbers 1 and 2 above!
Rotation Rules:

Where did these rules come from?
To derive our rotation rules, we can take a look at our first example, when we rotated triangle ABC 90º counterclockwise about the origin. If we compare our coordinate point for triangle ABC before and after the rotation we can see a pattern, check it out below:
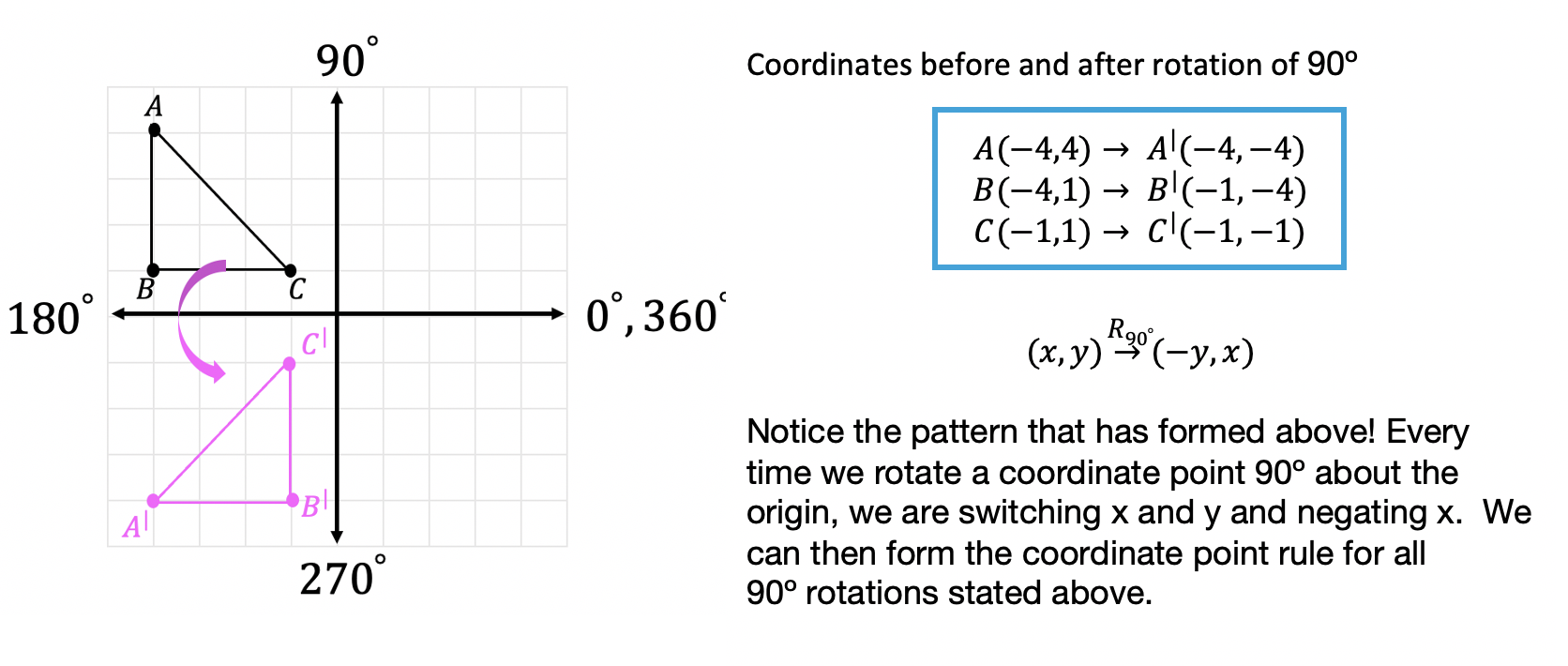
The rotation rules above only apply to those being rotated about the origin (the point (0,0)) on the coordinate plane. But points, lines, and shapes can be rotates by any point (not just the origin)! When that happens, we need to use our protractor and/or knowledge of rotations to help us find the answer. Let’s take a look at the Examples below:
Example #1:
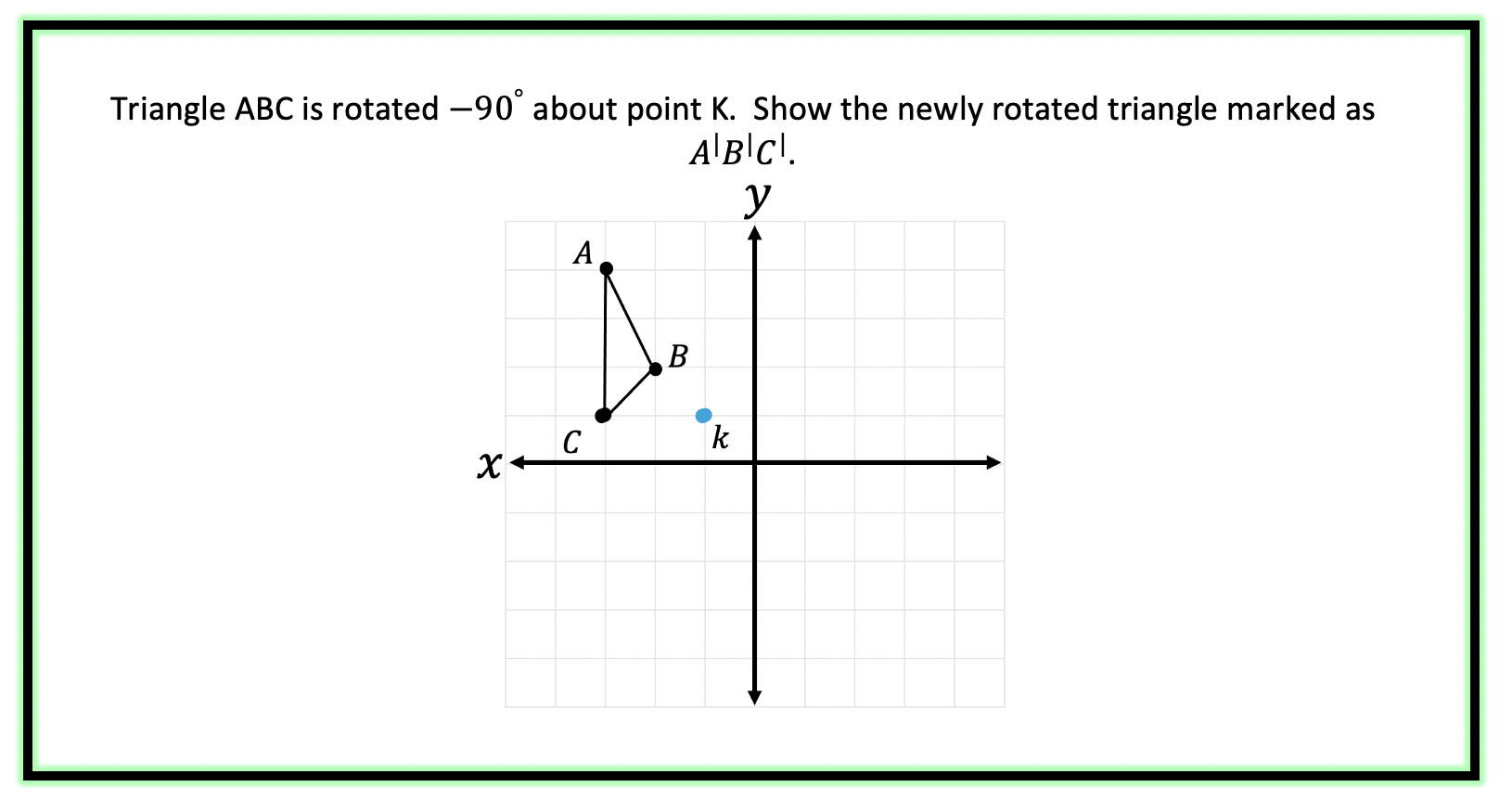
Step 1: First, let’s look at our point of rotation, notice it is not the origin we rotating about but point k! To understand where our triangle is in relation to point k, let’s draw an x and y axes starting at this point:
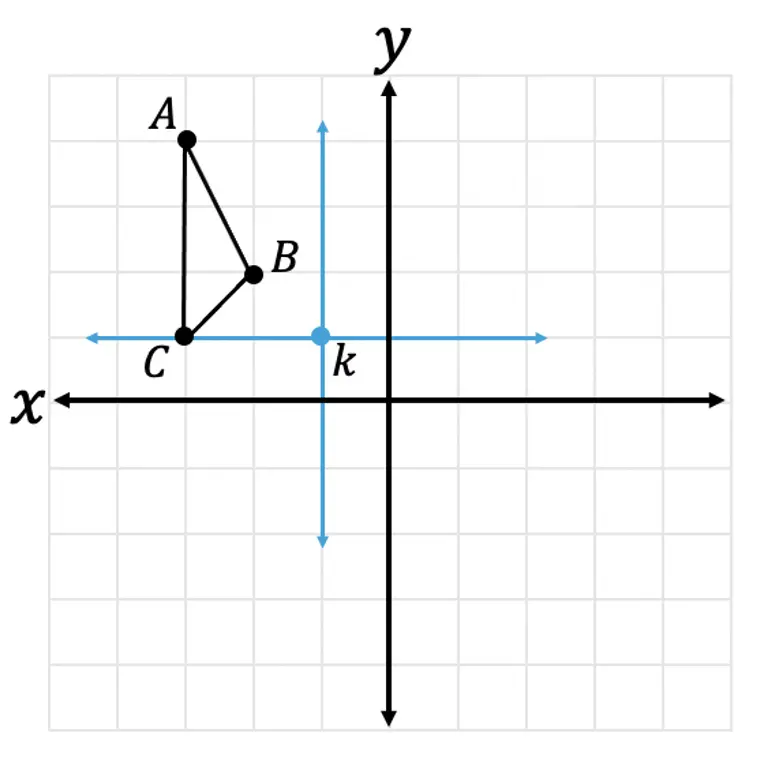
Step 2: Now let’s look at the coordinate point of our triangle, using our new axes that start at point k.
Step 2: Next, let’s take a look at our rule for rotating a coordinate -90º and apply it to our newly rotated triangles coordinates:
Step 3: Now let’s graph our newly found coordinate points for our new triangle .
Step 4: Finally let’s connect all our new coordinates to form our solution:
Another type of question with rotations, may not involve the coordinate plane at all! Let’s look at the next example:
Example #2:
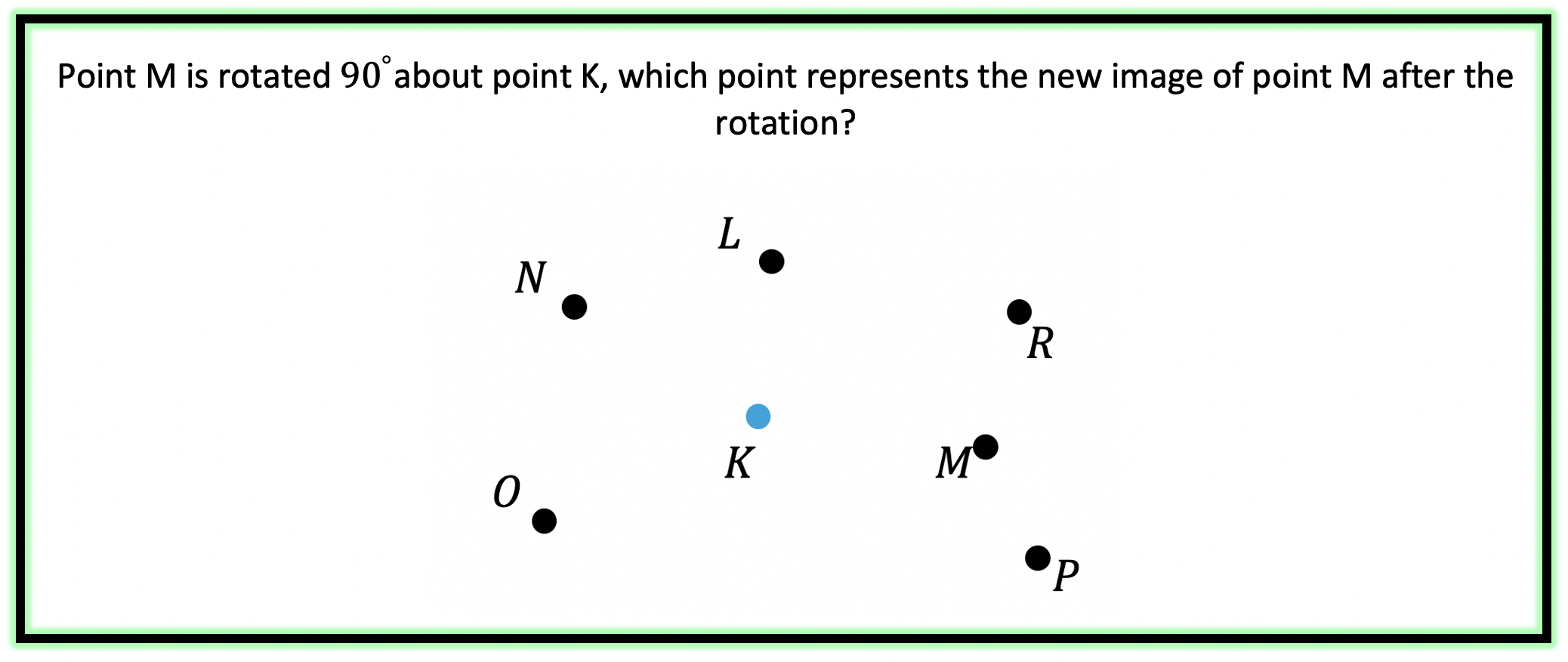
Step 1: First, let’s identify the point we are rotating (Point M) and the point we are rotating about (Point K).
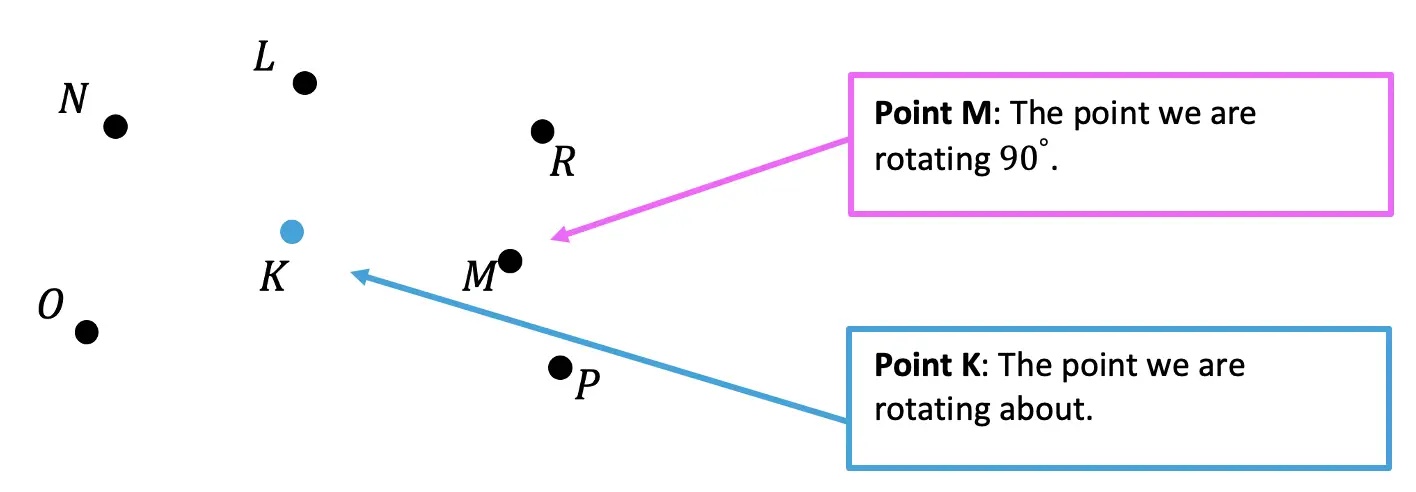
Step 2: Next we need to identify the direction of rotation. Since we are rotating Point M 90º, we know we are going to be rotating this point to the left in the clockwise direction.
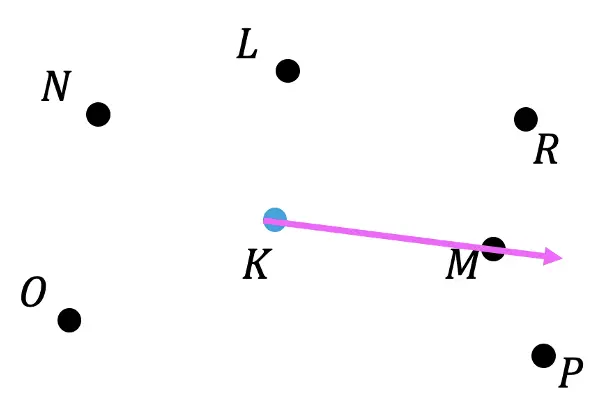
Step 3: Now we can draw a line from the point of origin, Point K, to Point M.
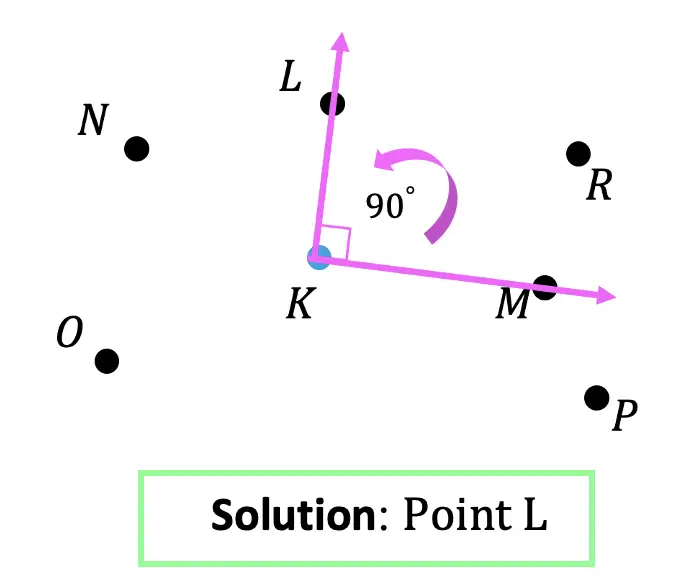
Step 4: Now, using a protractor and ruler, measure out 90º, draw a line, and notice that point L lands on our 90º line. This is our solution! (Note: For help on how to use a protractor, check out the video above).
Ready for more? Check out the practice questions below to master your rotation skills!
Practice Questions:
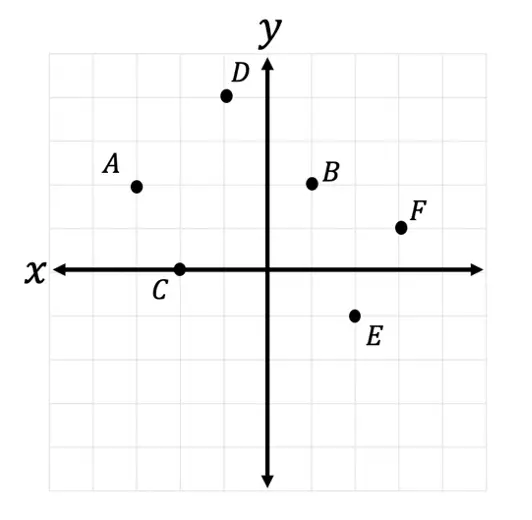
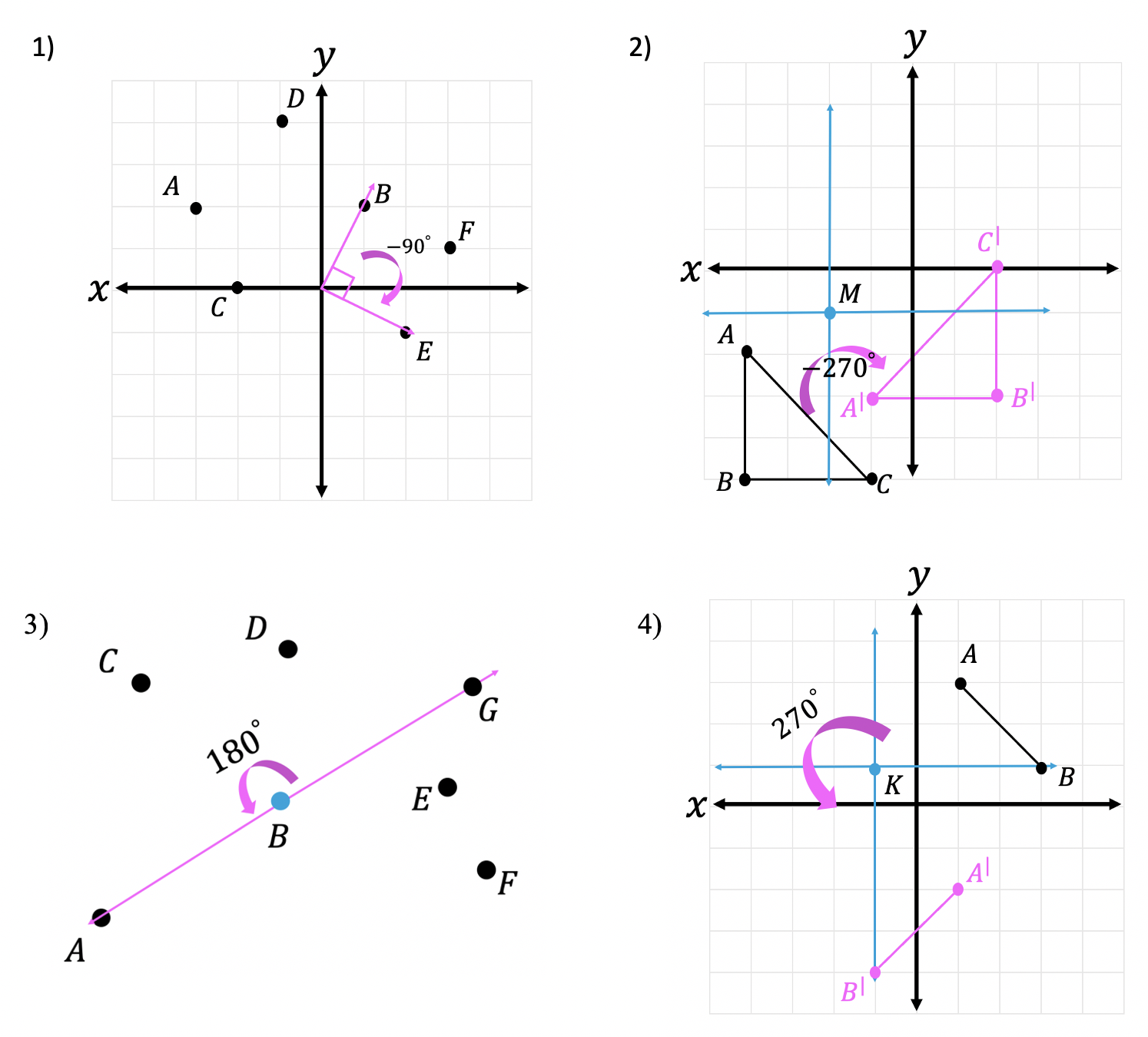
- Point B is rotated -90º about the origin. Which point represents newly rotated point B?
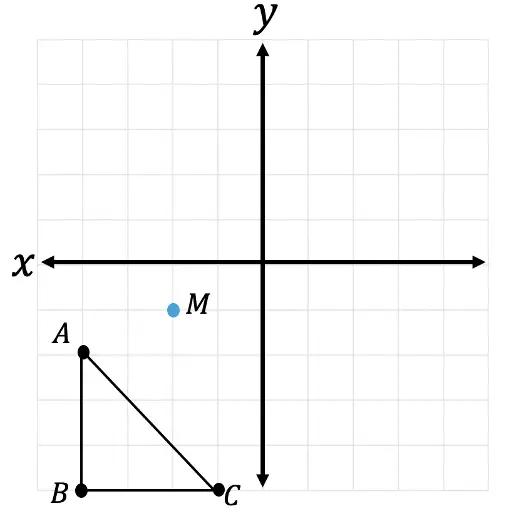
2. Triangle ABC is rotated -270º about point M. Show newly rotated triangle ABC as A prime B prime C prime.
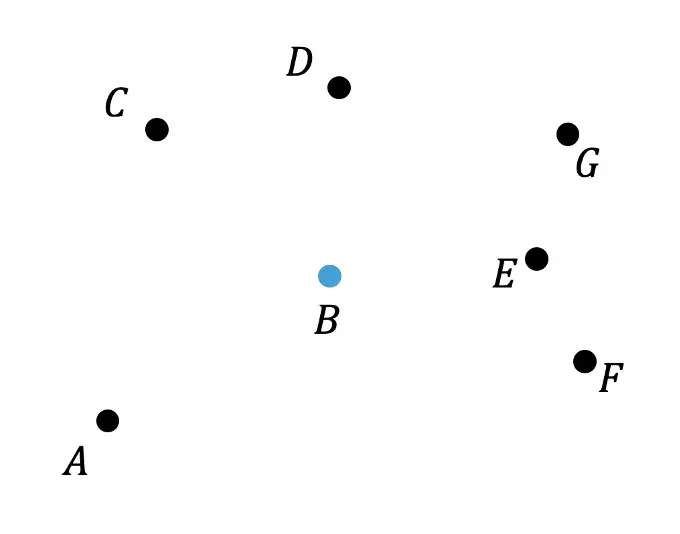
3. Point G is rotated about point B by 180º. Which point represents newly rotated point B?
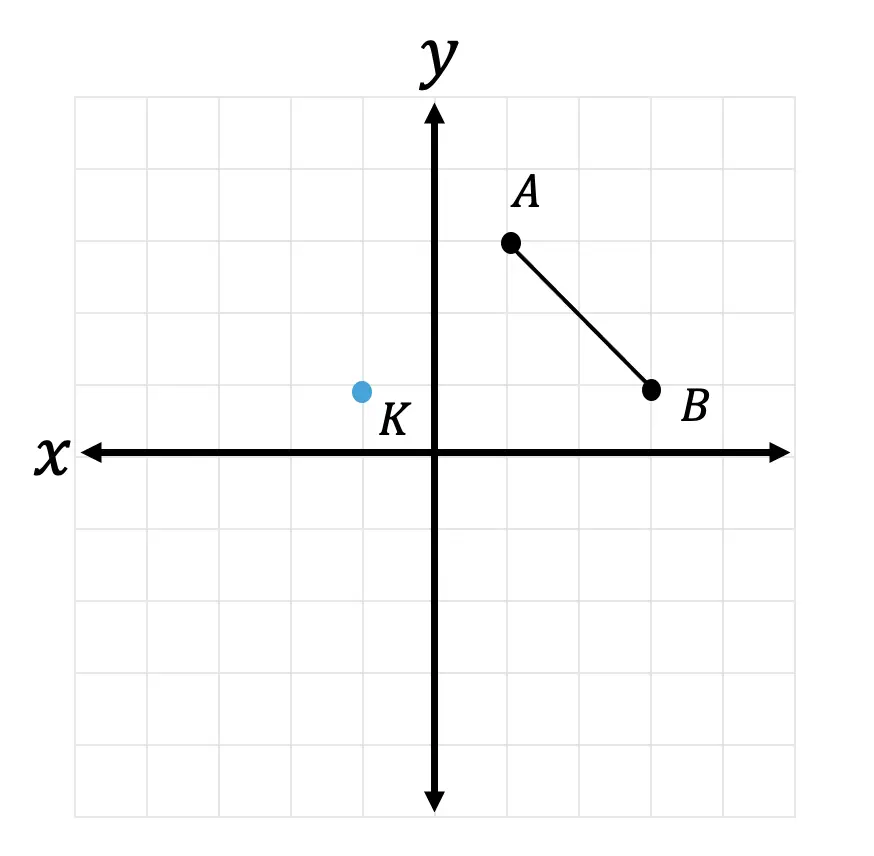
4. Segment AB is rotated 270º about point K. Show newly rotated segment AB.
Solutions:
Still got questions on how to rotations about a point? No problem! Don’t hesitate to comment with any questions or check out the video above for even more examples. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Looking for more Transformations? Check out the related posts below!
