Happy Wednesday math peeps! This post introduces constructions by showing us how to construct an equilateral triangle by using a compass and straightedge (or ruler). For anyone new to constructions in geometry, this is the perfect topic for art aficionados since there is more drawing here than there is actual math!
What is an Equilateral Triangle?
Equilateral Triangle: An equilateral triangle is a triangle with three equal sides. Not an easy one to forget, the equilateral triangle is super easy to construct given the right tools (compass+ straightedge). Take a look below:

Construct an Equilateral Triangle Example:

Check out the GIF below to see how to construct an equilateral triangle step by step using a compass and straightedge with pictures and explanations below!
Solution:
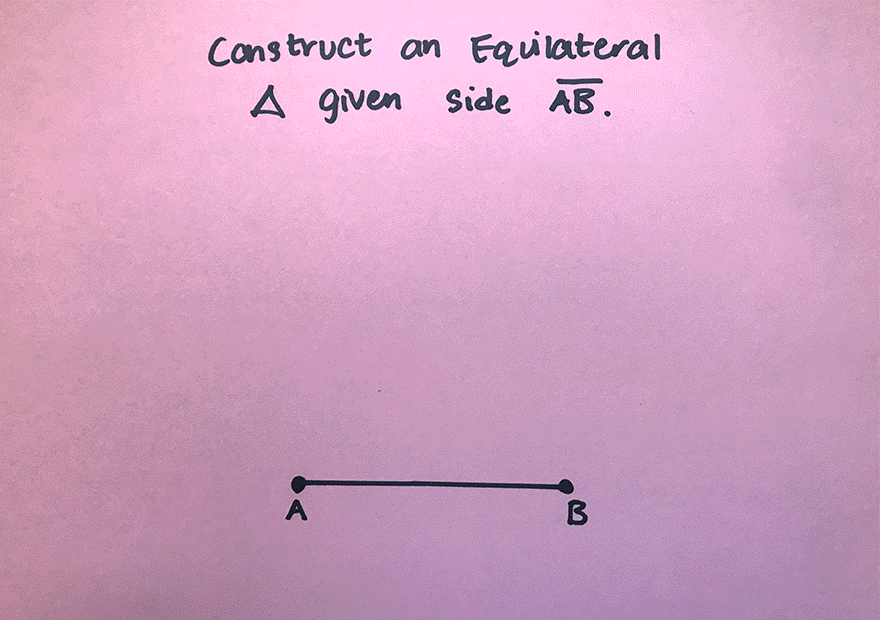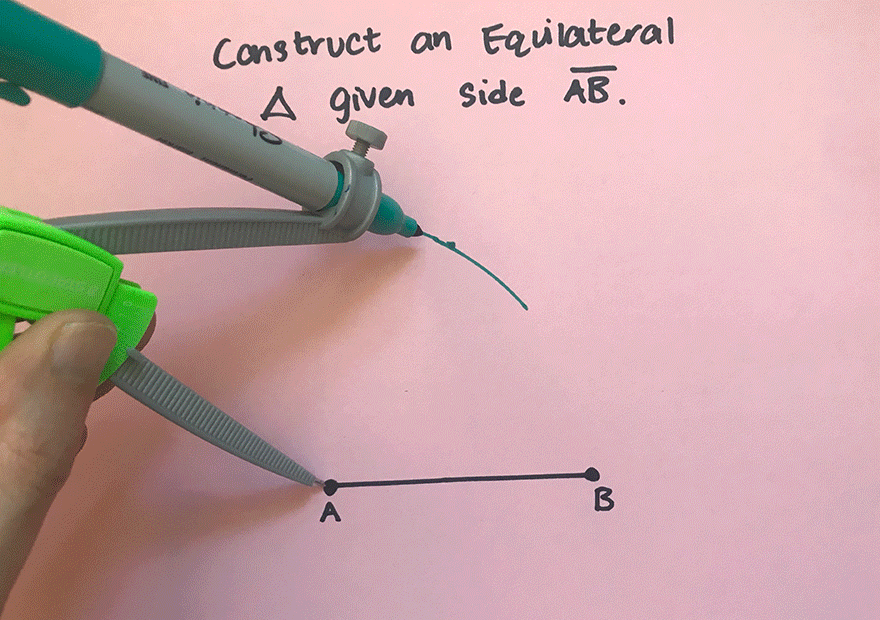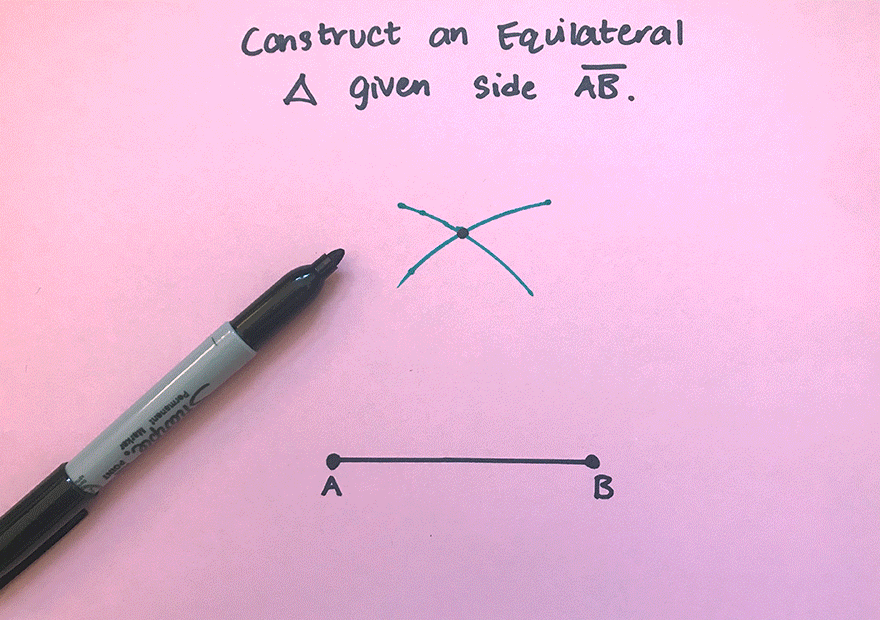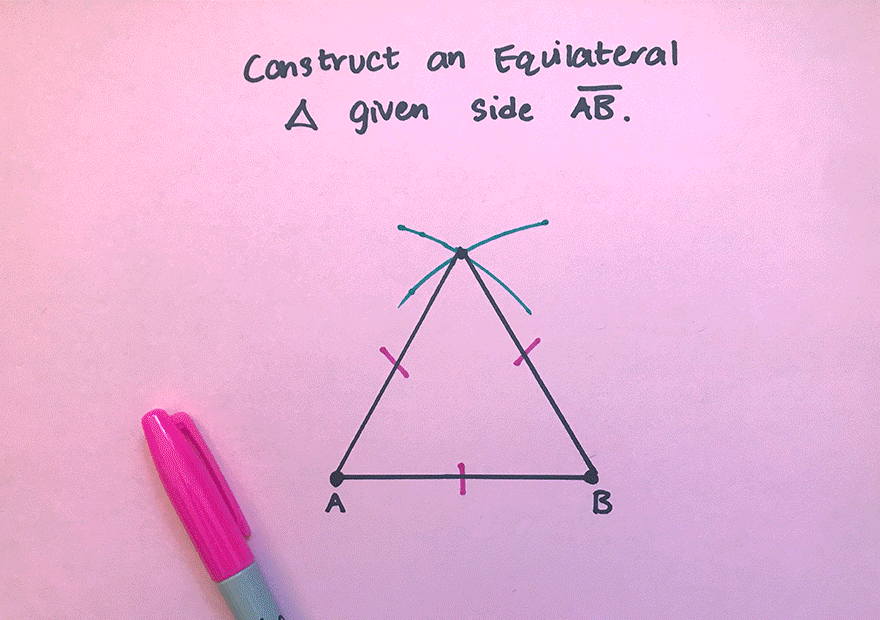
What’s Happening in this GIF?
1. Using a compass, we measure the distance of line segment ![]() .
.
2. With the compass point remaining on point A, we then draw an arc that has the same distance as line segment ![]() .
.
3. With the compass now placed on point B, draw an arc that has the same distance as line segment ![]() .
.
4. Notice where the arcs intersect? Using a ruler, connect points A and B to the new intersection point. This will create two new equal sides of our triangle!
5. We have now officially constructed a triangle with all equal side lengths!
Constructions and Related Posts:
Looking to construct more than just an equilateral triangle? Check out these related posts on geometry constructions!
Construct a Perpendicular Bisector
Perpendicular Line through a Point
Altitudes of a Triangle (Acute, Obtuse, Right)
Construct a Square inscribed in a Circle
Best Geometry Tools!
Looking to get the best construction tools? Any compass and straight-edge will do the trick, but personally, I prefer to use my favorite mini math toolbox from Staedler. Stadler has a geometry math set that comes with a mini ruler, compass, protractor, and eraser in a nice travel-sized pack that is perfect for students on the go and for keeping everything organized….did I mention it’s only $7.99 on Amazon?! This is the same set I use for every construction video in this post. Check out the link below and let me know what you think!
Still got questions? No problem! Don’t hesitate to comment with any questions. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Looking to learn more about triangles? Check out this post on right triangle trigonometry here! And if you’re looking for even more geometry constructions, check out the link here!