Greetings math friends! In this post, we arere going to go over the formulas for Variance and Standard Deviation. We will take this step by step by explaining the significance of the variance and standard deviation formulas in relation to a set of data. Get your calculators ready because this step by step although not hard, will take some serious number crunching! Also, don’t forget to check out the video on standard deviation and variance below to see how to check your work using a calculator. Happy calculating! 🙂
If you’re looking for related formulas, Mean Absolute Deviation (MAD) and Expected Value, scroll to the bottom of this post! And if you’re interested we’ll also touch upon the difference between population variance and sample variance later in this post.
What is the Variance?
The variance represents the spread of data or the distance each data point is from the mean. When we have multiple observations in our data, we want to know how far each unit of data is from the mean. Are all the data points close together or spread far apart? What is the probability distribution? This is what the variance will help tell us!
Don’t freak out but here’s the formula for variance, notated as using the greek letter, sigma squared, σ2:
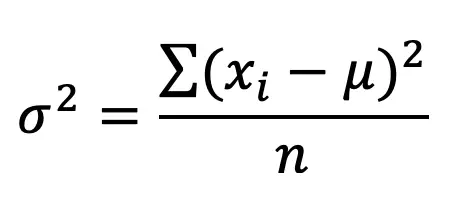
where…
xi= Value of Data Point
μ= mean
n=Total Number of Data Points]
(xi-μ)=Distance each data point is to the mean
In plain English, this translates to:
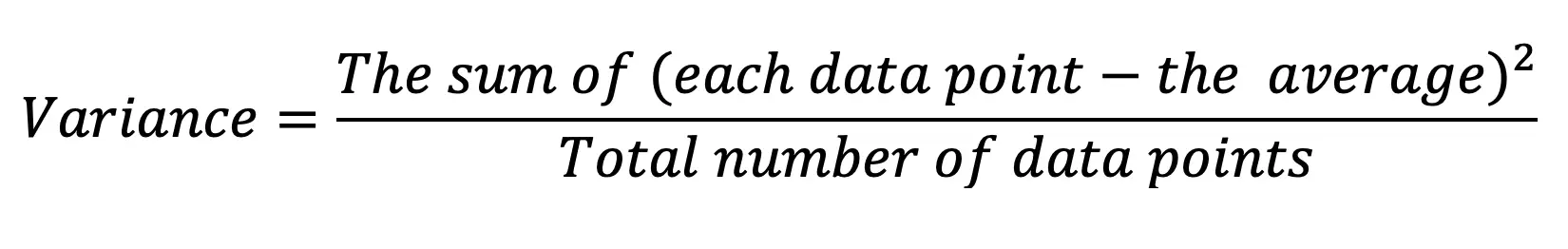
Let’s try an example to find the standard deviation and variance of the data set below.

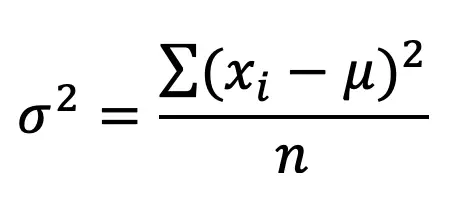
Step 1: First, let’s find the mean, μ.
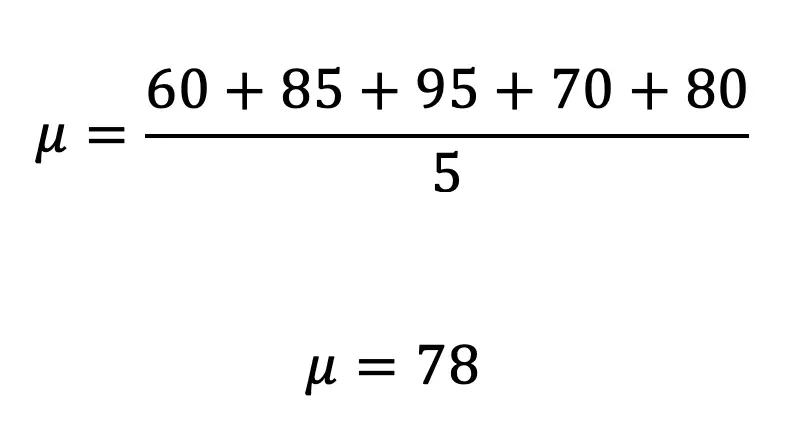
Step 2: Now that we have the mean, we are going to do each part of our formula one step at a time in the table below.
Notice we subtract each test score from the mean, μ=78. Then we square the result of each subtracted test score to get the squared deviation of each data value, then finally sum all the squared results together.
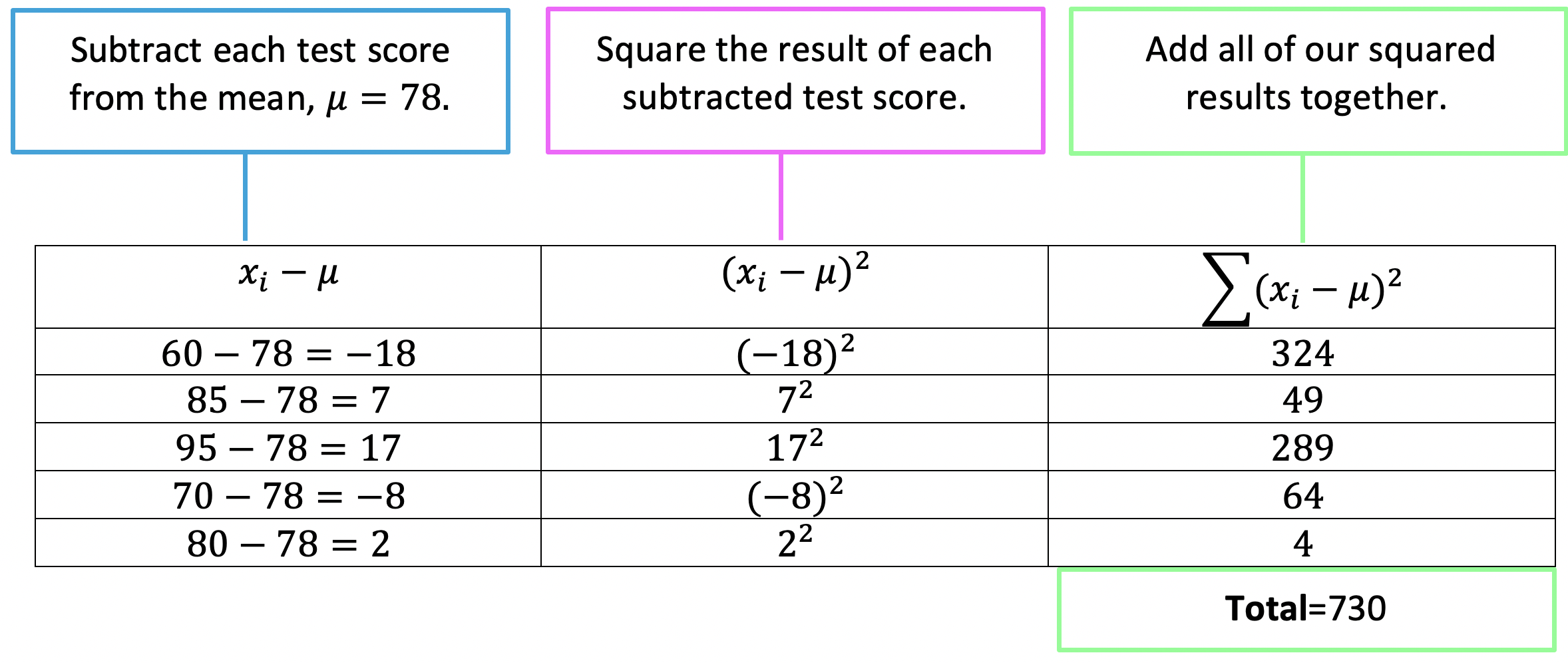
Step 3: Now that we summed all of our squared deviations, to get 730, we can fill this in as our numerator in the variance formula. We also know our denominator is equal to 5 because that is the total number of test scores in our data set.


What is Standard Deviation?
Standard deviation is a unit of measurement that is unique to each data set and is used to measure the spread of data. The standard deviation formula happens to be very similar to the variance formula!
Below is the formula for standard deviation, notated as sigma, the greek letter, σ:

Since this is the same exact formula as variance with a square root, all we need to do is take the square root of the variance to find standard deviation:

Sample VS. Population
What is the difference between a sample vs. a population?
A population in statistics refers to an entire data set that at times can be humanly incapable of reaching.
For example: If we wanted to know the average income of everyone who lives in New York State, it would be almost impossible to reach every working person and ask them how much they make for a living.
To make up for the impossibility of data collection, we usually only survey a sample of the entire population to get income levels of let’s say 10,000 people across New York State, a much more reasonable in terms of data collecting!
And taking this sample size from the entire working population of New York State provides us with a sample mean, a sample variance, and a sample standard deviation.
On the other hand, if we were able to ask every student in a school what their grade point average was and get an answer, this would be an example of a whole population. Using this information, we would be able to find the population mean, population variance, and population standard deviation.
Sample notation also differs from population notation, but don’t worry about these too much, because the formulas and meanings remain the same. For example, the population mean is represented by the greek letter, μ, but the sample mean is represented by x bar.
Now try calculating the standard deviation of each data set below on your own with the following practice problems!
Practice Questions:

Solutions:
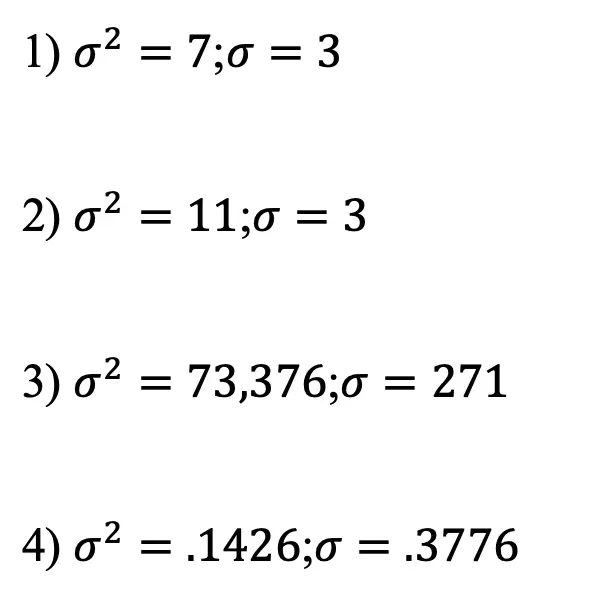
Other Related Formulas
Mean Absolute Deviation (MAD):
The Mean Absolute Deviation otherwise known as MAD is another formula related to variance and standard deviation. In the MAD formula above, notice we are doing very similar steps, by finding the distance to the mean of each data point, only this time we are taking the aboslute value of the ditsance to the mean. Then we sum all the absolute value distances together and divide by the total number of data points.
Why do we use aboslute value in this formula? We take the absolut value, because if didn’t the distance to the means summed togther would cancel eachother out to get zero!
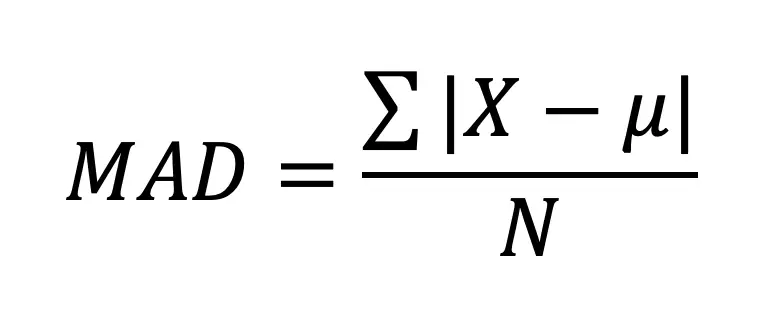
Where…
X = Data point value
μ = mean
N=Total number of data points
|X-μ|=absolute deviation
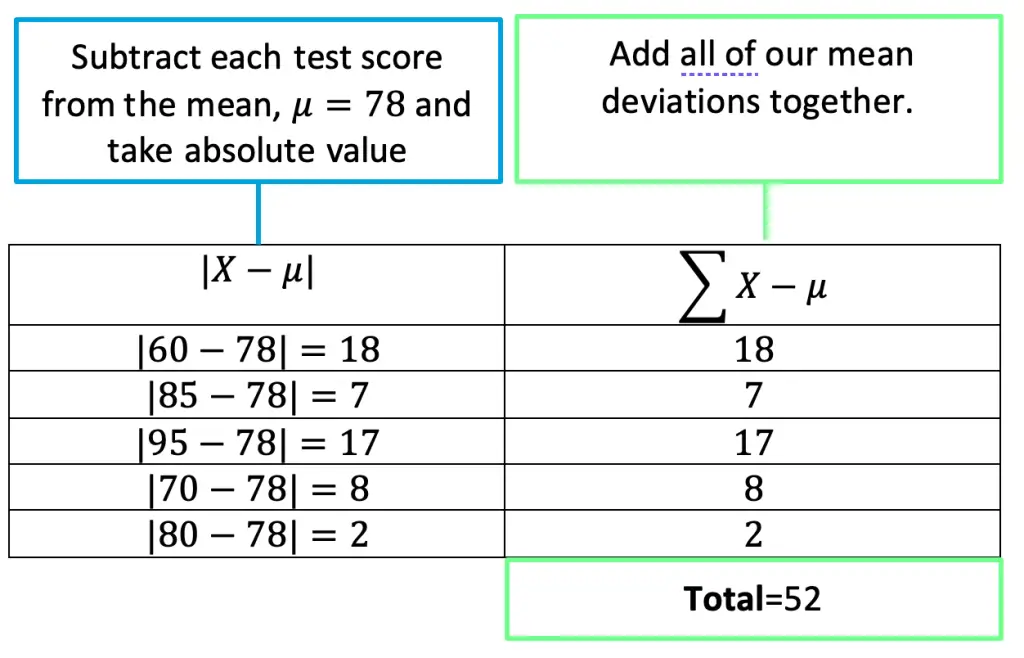
If we were to take the sample from our example earlier,60, 85, 95, 70, 80, in this post and find the MAD it would go something like this:

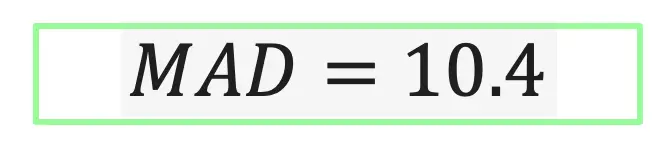
Expected Value:
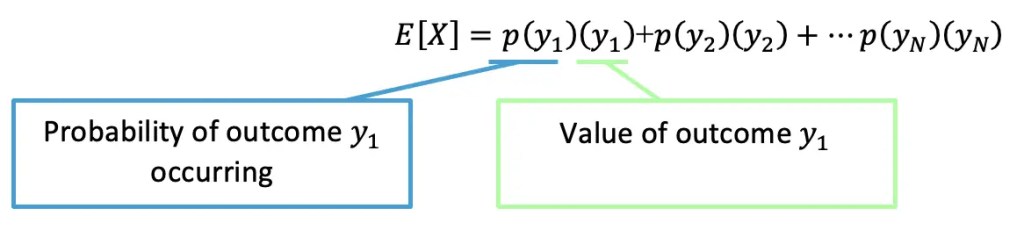
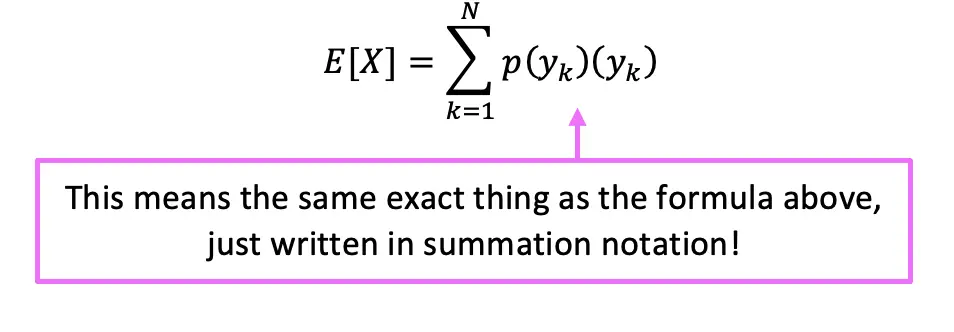
Expected Value is the weighted average of all possible outcomes of one “game” or “gamble” based on the respective probabilities of each potential outcome for a discrete random variable. A “gamble” is defined by the following rules: 1) All possible outcomes are known 2) An outcome cannot be predicted 3) All possible outcomes are of numeric value and 4) The Game can be repeated multiple times under the same conditions.
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Also! If you’re looking for more statistics, check out this post on how to create and analyze box and whisker plots here!

2 thoughts on “Variance and Standard Deviation: Statistics”