Hi everyone and welcome to MathSux! In this post, we are going to break down 30 60 90 degree special right triangles. What is it? Where did it come from? What are the ratios of its side lengths and how do we use them? You will find all of the answers to these questions about this right angled triangle in this post. Also, don’t forget to check out the video below and practice questions at the end of this post to truly become a 30 60 90 special right triangle master! Happy calculating! 🙂
If you want to learn about the other special triangle, 45 45 90 triangle, check out this post here. And if you’re looking to make math suck just a little bit less? Subscribe to our Youtube channel for free math videos every week! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
30 60 90 Triangle Ratio:
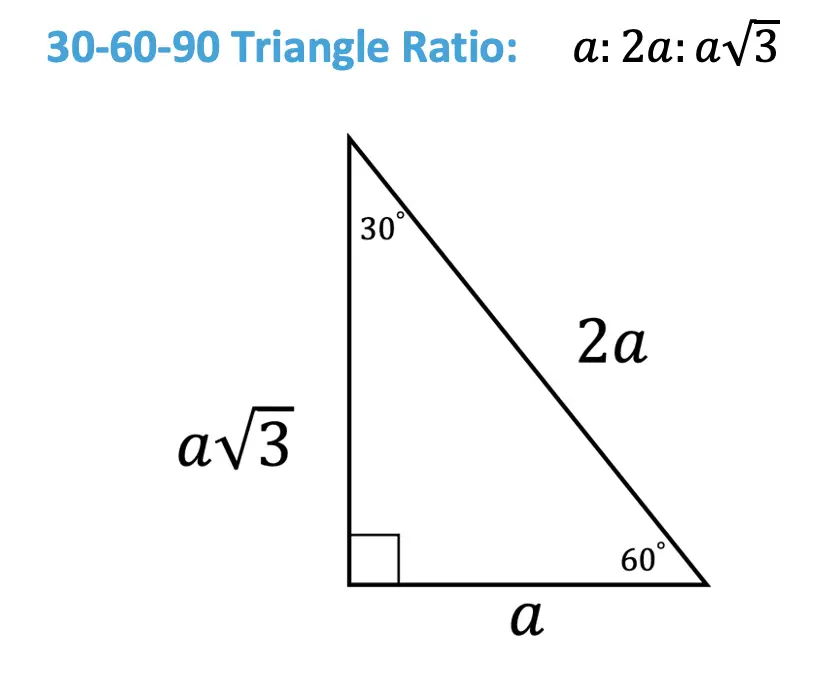
Notice that the 30 60 90 triangle is made up of one right angle across from the hypotenuse (which is always going to be the longest side), a 60 degree angle with a longer leg on the opposite side, and a 30 degree angle measure across from the shorter leg.
What is a 30 60 90 Triangle and why is it “Special”?
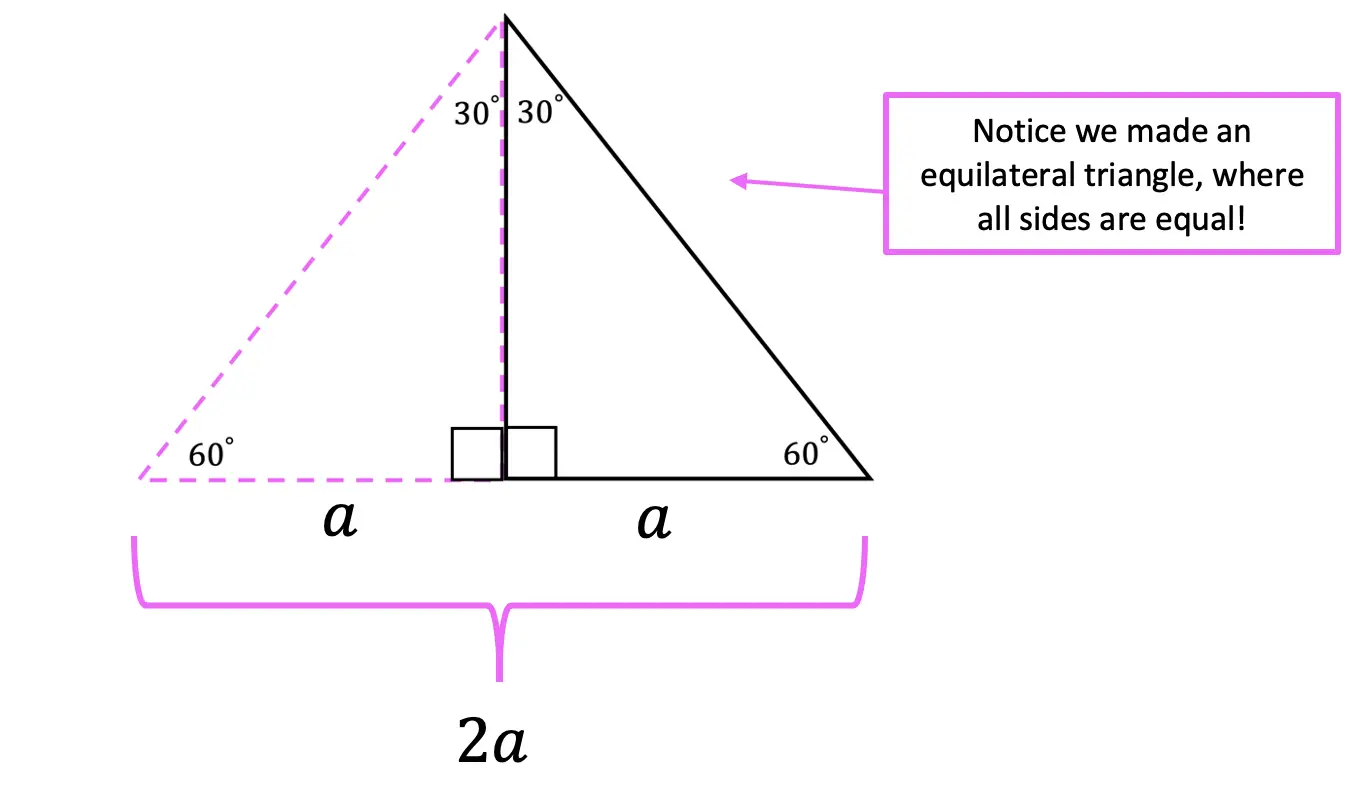
The 30 60 90 triangle is a special right triangle because it forms an equilateral triangle when a mirror image of itself is drawn. This means that all sides are equal when a mirror image of the triangle is drawn which allows us to find the ratio between each of the sides of the triangle by using the Pythagorean Theorem. Check it out below!
Now let’s draw a mirror image of our triangle to create an equilateral triangle. Next, we can label the length of the new side opposite 30 degrees (the shorter leg) “a,” and add this new mirror image length with the original we had to get, a total of a+a=2a.
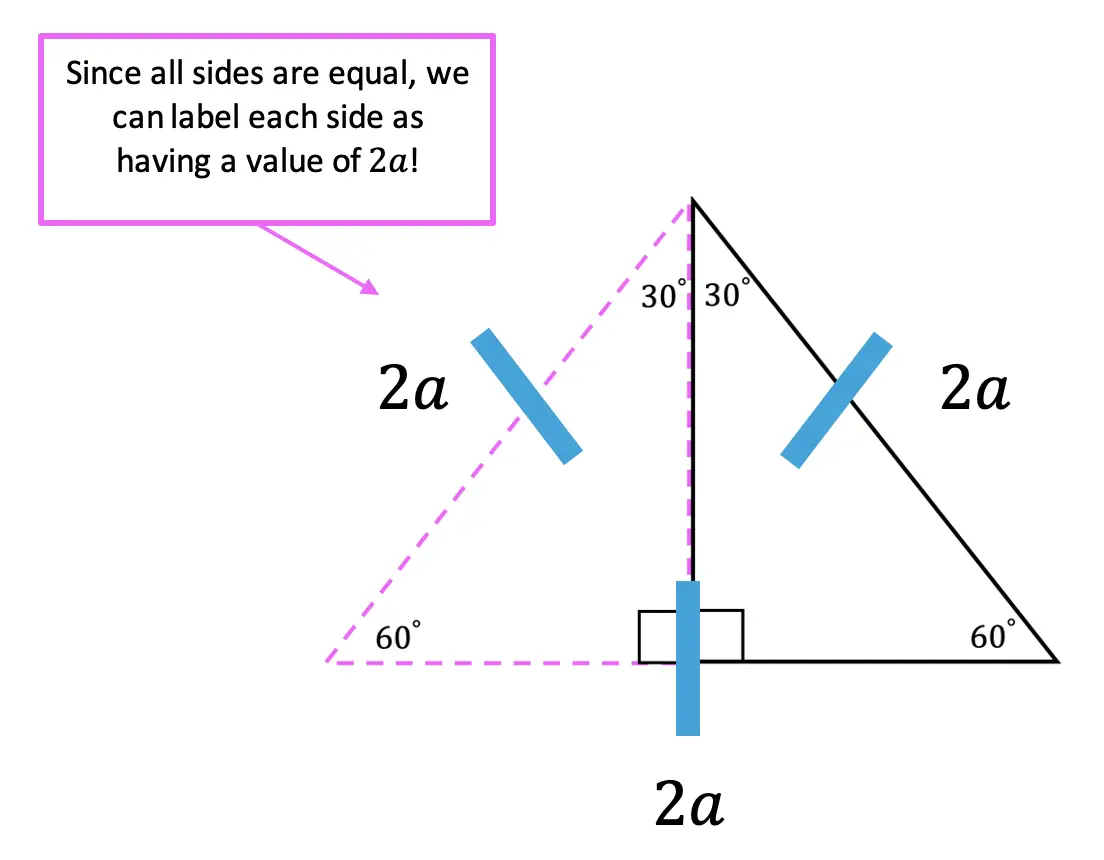
If we look at our original 30 60 90 triangle, we now have the following values for each side based on our equilateral triangle. Notice we still need to find the length value of the longer leg, opposite angle 60 degrees.
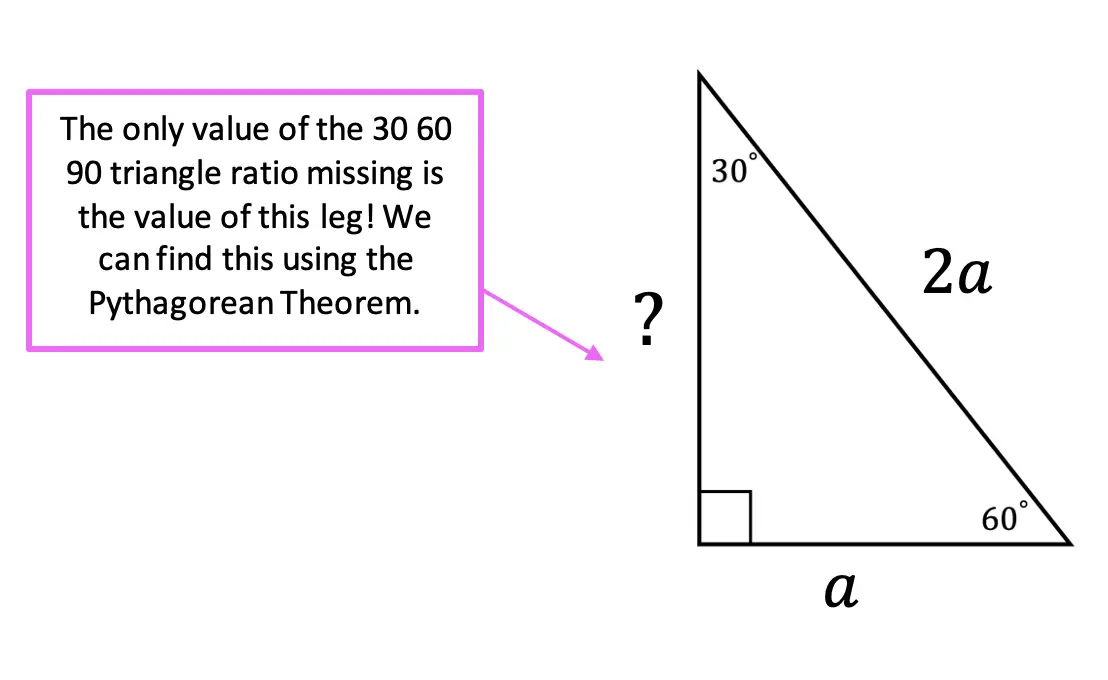

To sum up, we have applied the Pythagorean Theorem formula, filled in values found in our triangle for each length, distributed the exponent and subtracted a2 from both sides, took the square root, and finally found our solution for our ratio for the longer leg opposite 60 degrees.
Now we can re-label our triangle, knowing the length of the hypotenuse in relation to the two legs. This creates a ratio that applies to all 30 60 90 triangles!

How do I use this ratio?
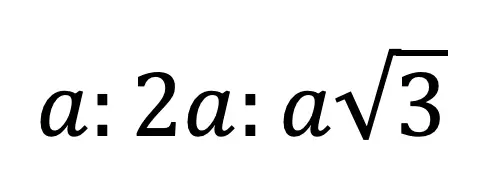
Knowing the above ratio, allows us to find any length of any and every 30 60 90 triangle, when given the value of one of its sides. Let’s tsee how this ratio works with some examples.
Example #1:
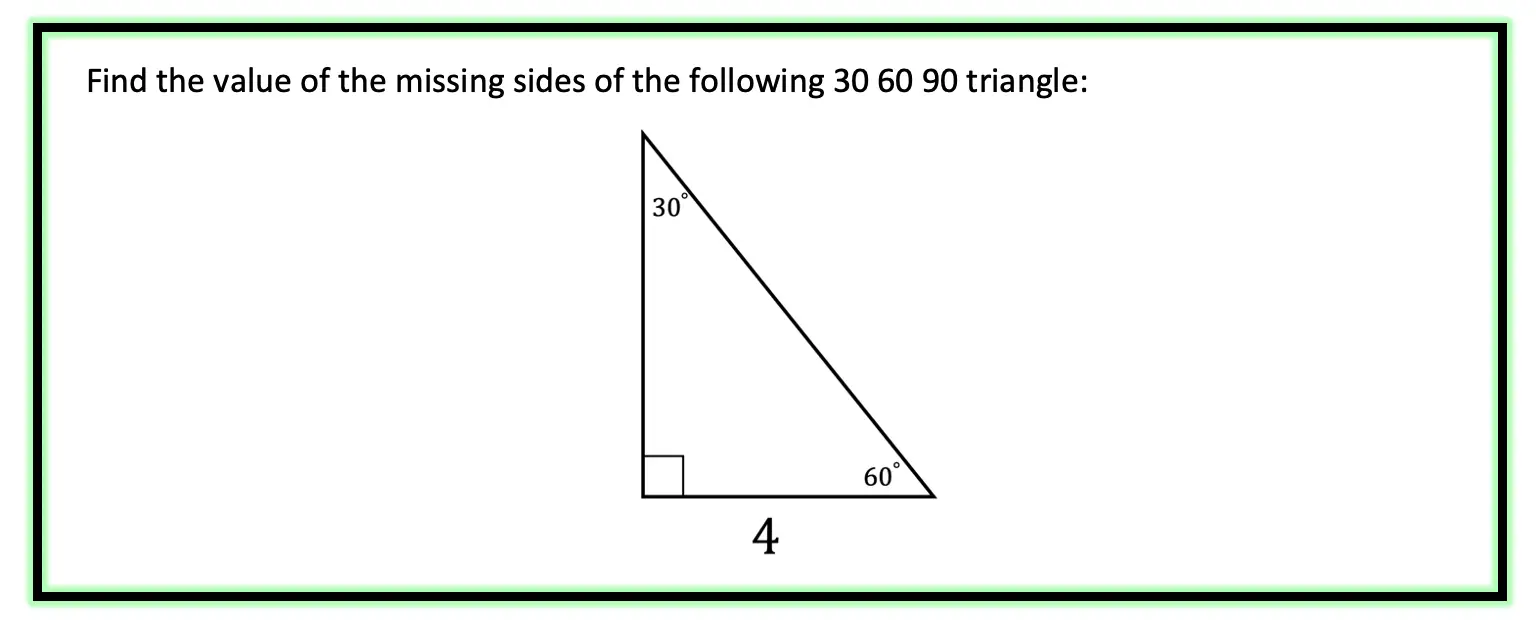
Step 1: First let’s look at our ratio and compare it to our given triangle.
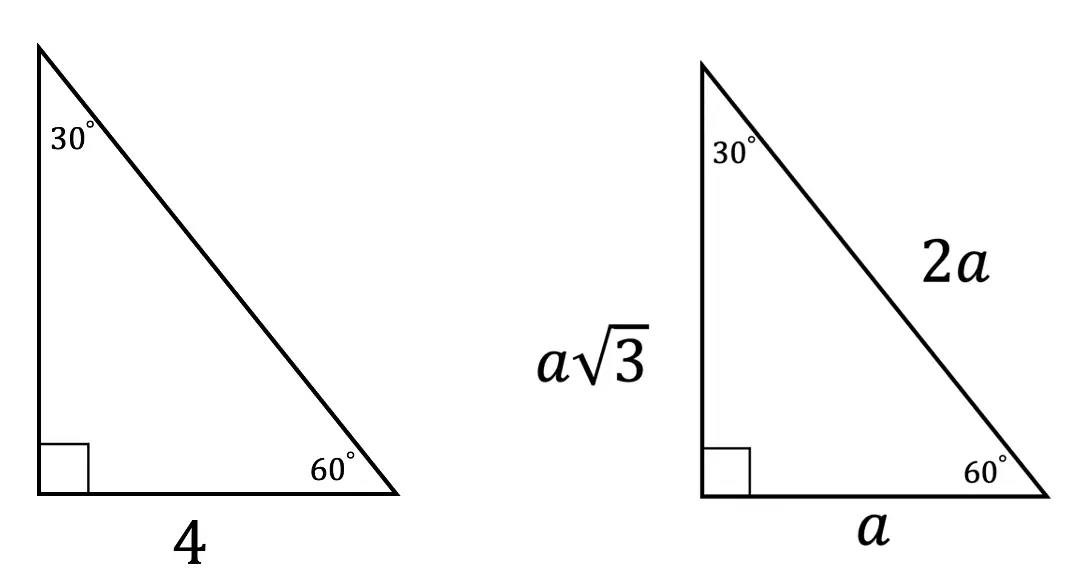
Step 2: Notice we are given the value of a, which is equal to 4, knowing this we can now fill in each length of our triangle based on the ratio of a 30 60 90 triangle.
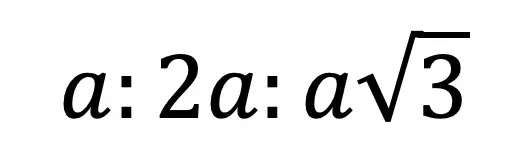
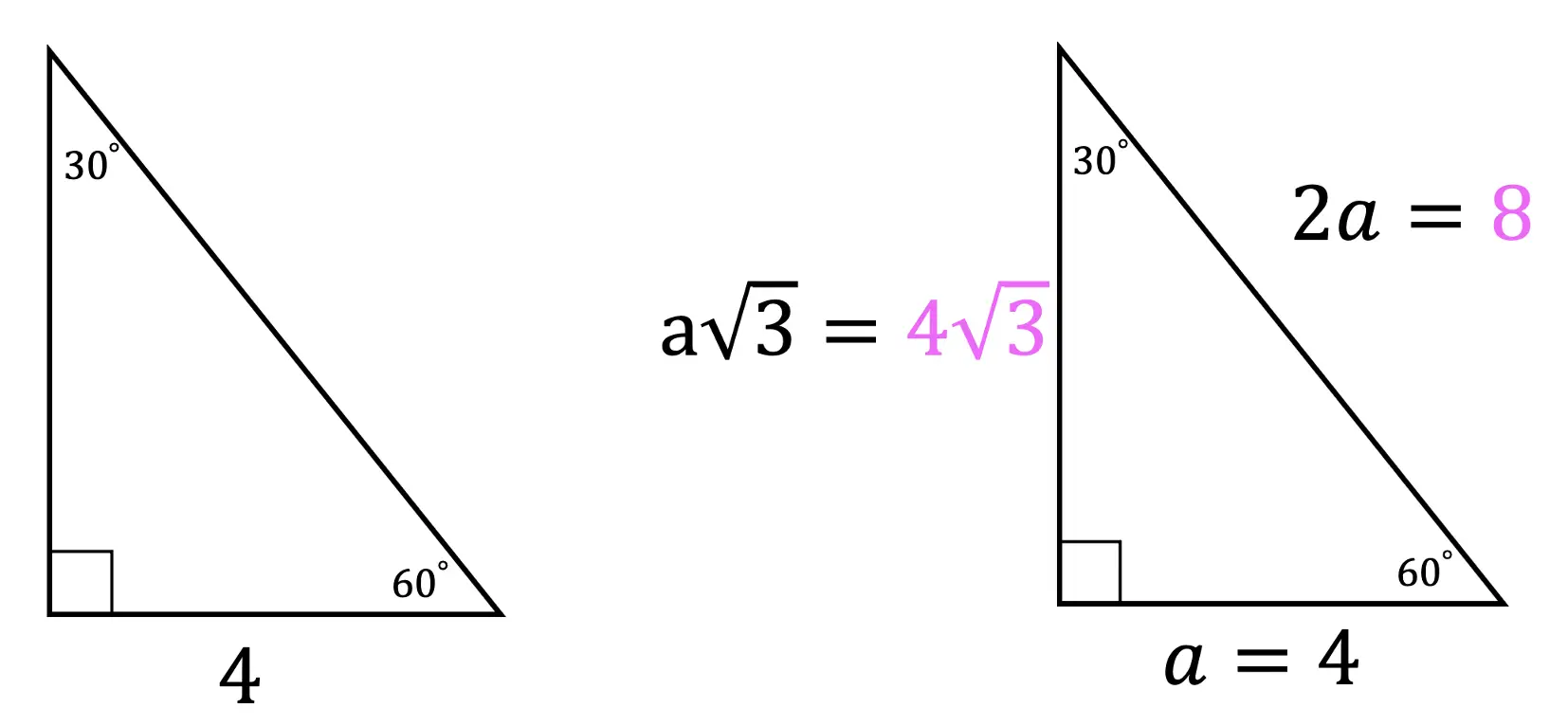
Now let’s look at another Example where we are given the length of the hypotenuse and need to find the values of the other two missing sides.
Example #2:
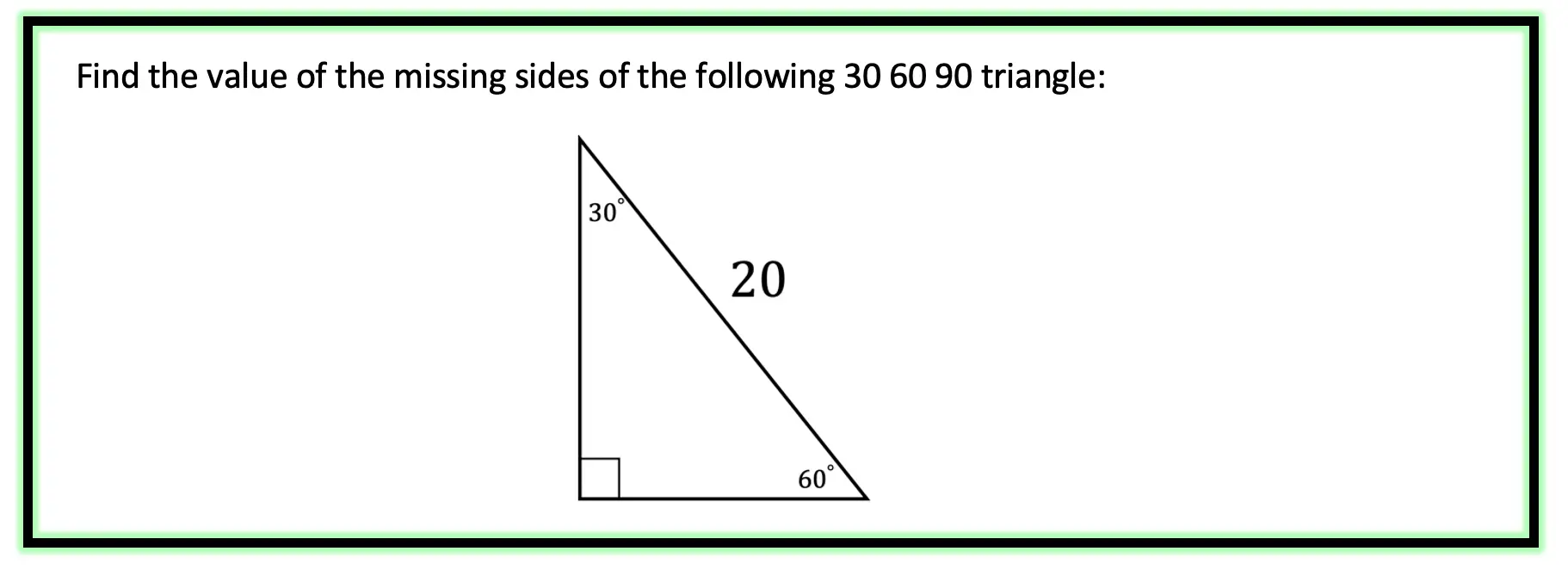
Step 1: First let’s look at our ratio and compare it to our given triangle.
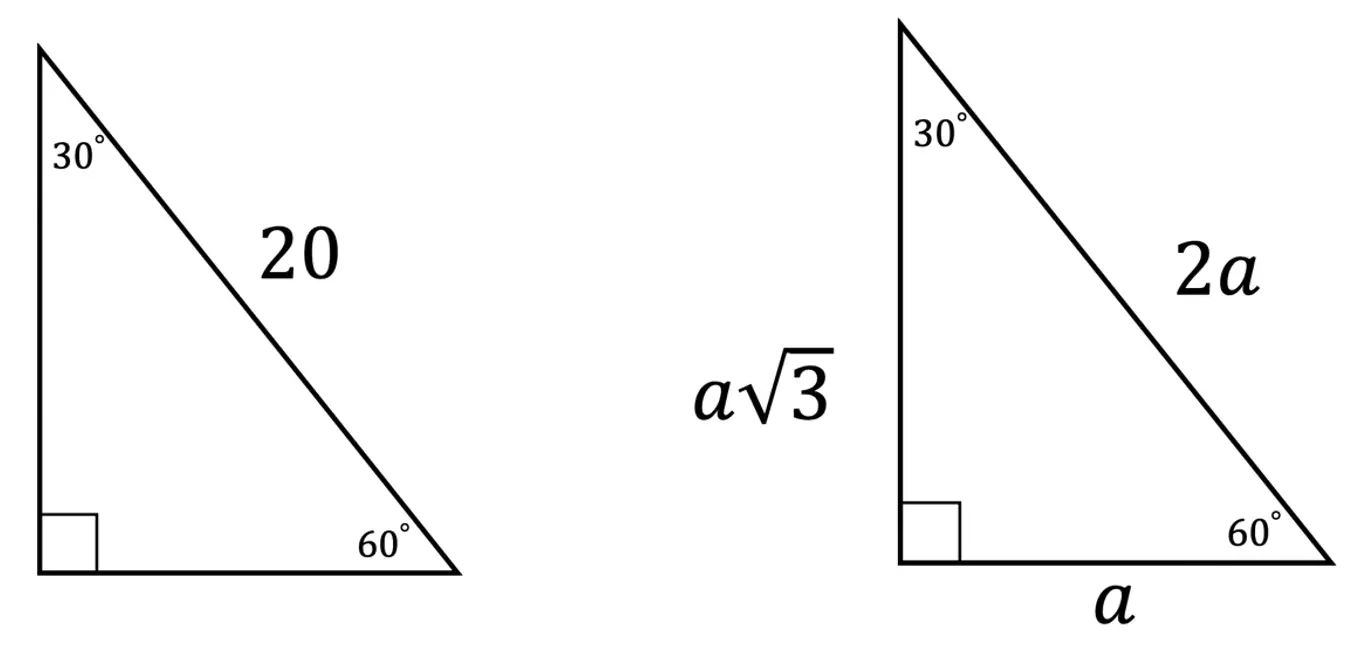
Step 2: Notice we are given the value of the hypotenuse, 2a=20. Knowing this we can find the value of a by dividing 20 by 2 to get a=10. Once we have the value of a=10, we can easily find the length of the last, longer leg based on the 30 60 90 ratio:
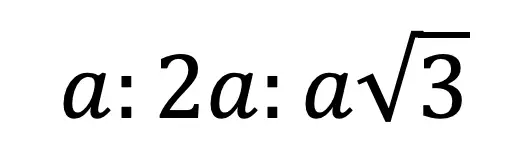
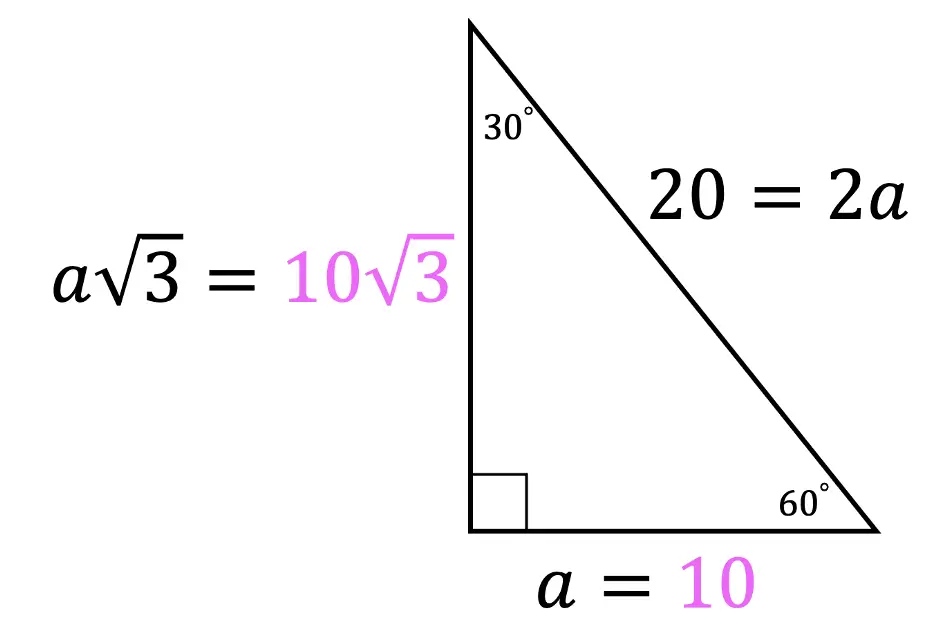
Now for our last Example, we will see how to find the value of the shorter leg and hypotenuse, when we are given the side length of the longer leg across from 60º and need to find the other two missing sides.
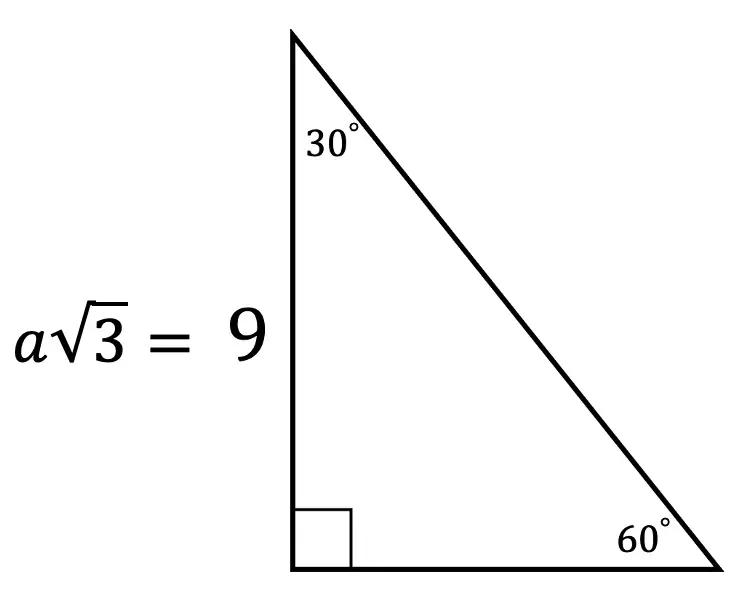
Example #3:
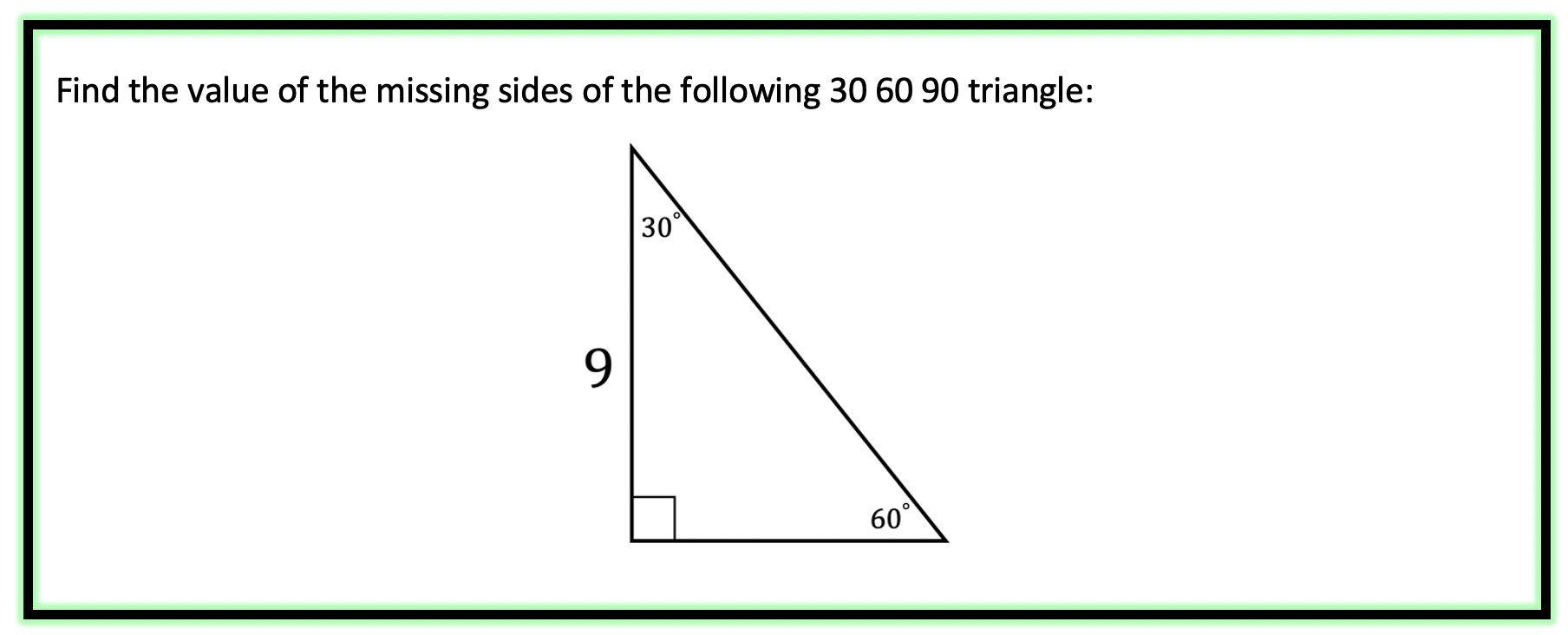
Step 1: First let’s look at our ratio and compare it to our given triangle.
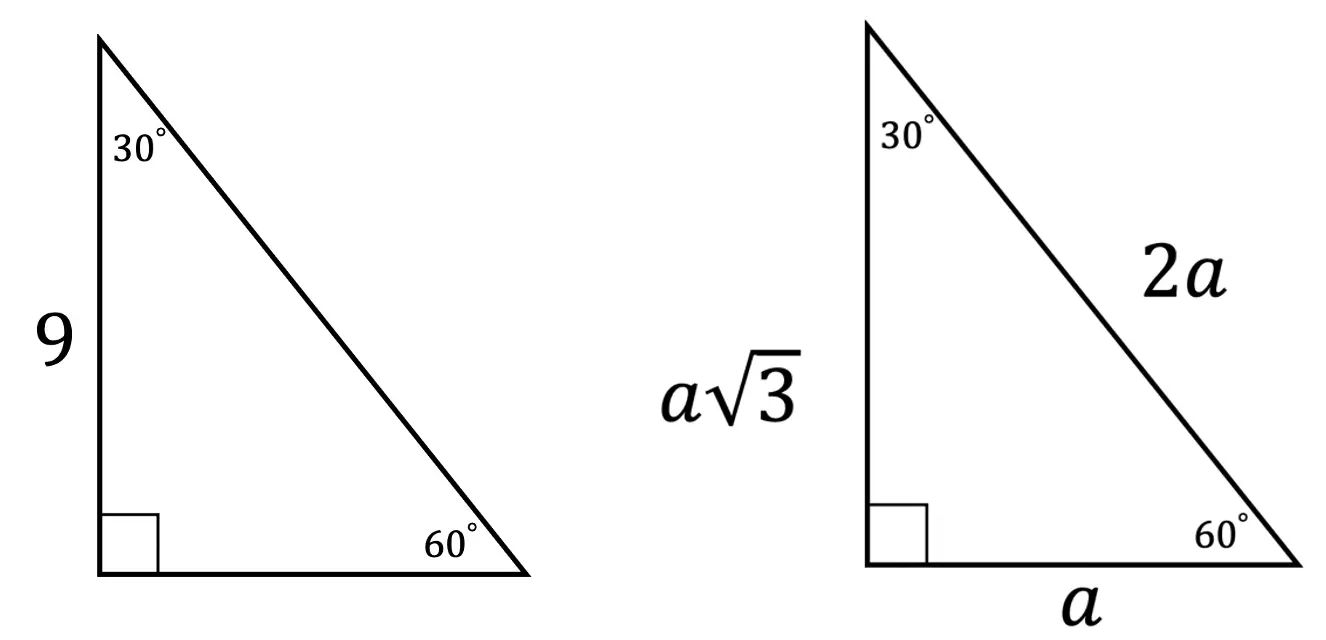
Step 2: In this case, we need to use little algebra to find the value of a, using the ratio for 30 60 90 triangles.
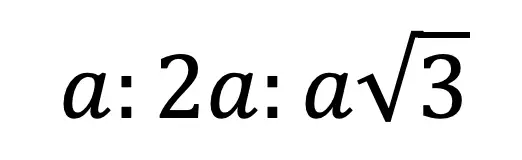

Now that we have one piece of the puzzle, the value of a, let’s fill in the value of the shorter leg of our triangle below:
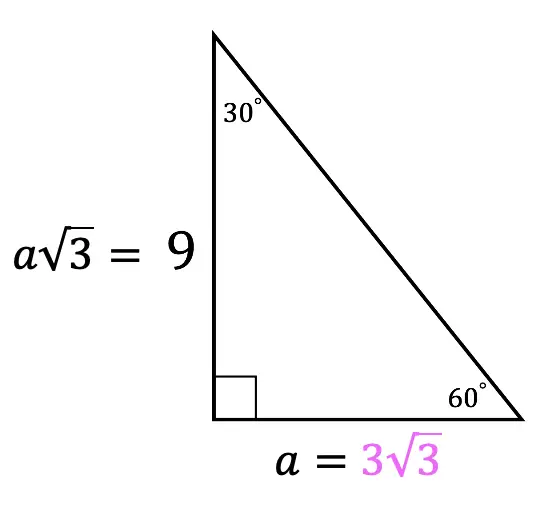
Finally, let’s find the value of the length of the hypotenuse, which is equal to 2a in our ratio. Knowing the length of all sides, we can fill in the lengths of each side of our triangle for our solution.
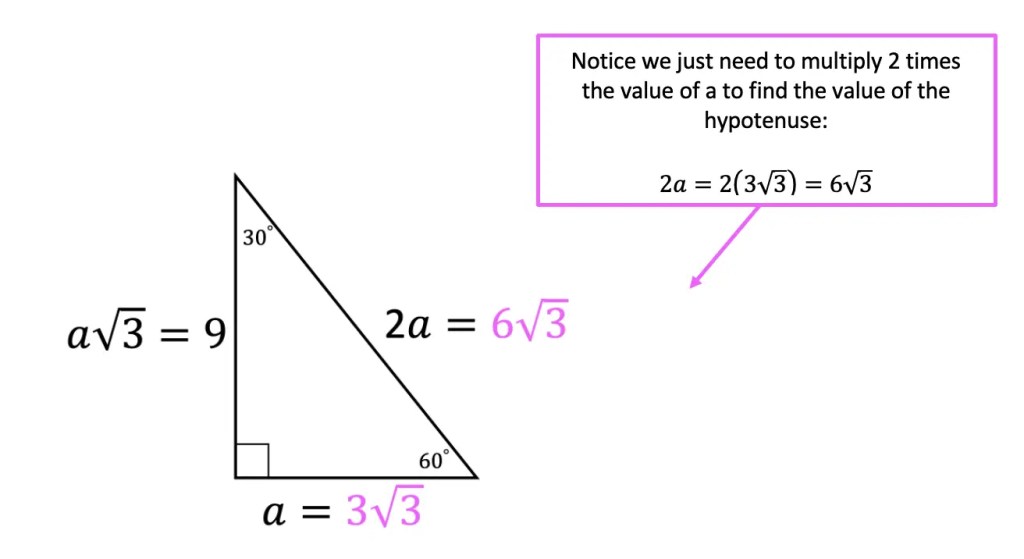
Think you are ready to master these types of questions on your own? Try the practice problems below!
Practice Questions:
Find the value of the missing sides of each 30 60 90 degree triangle.
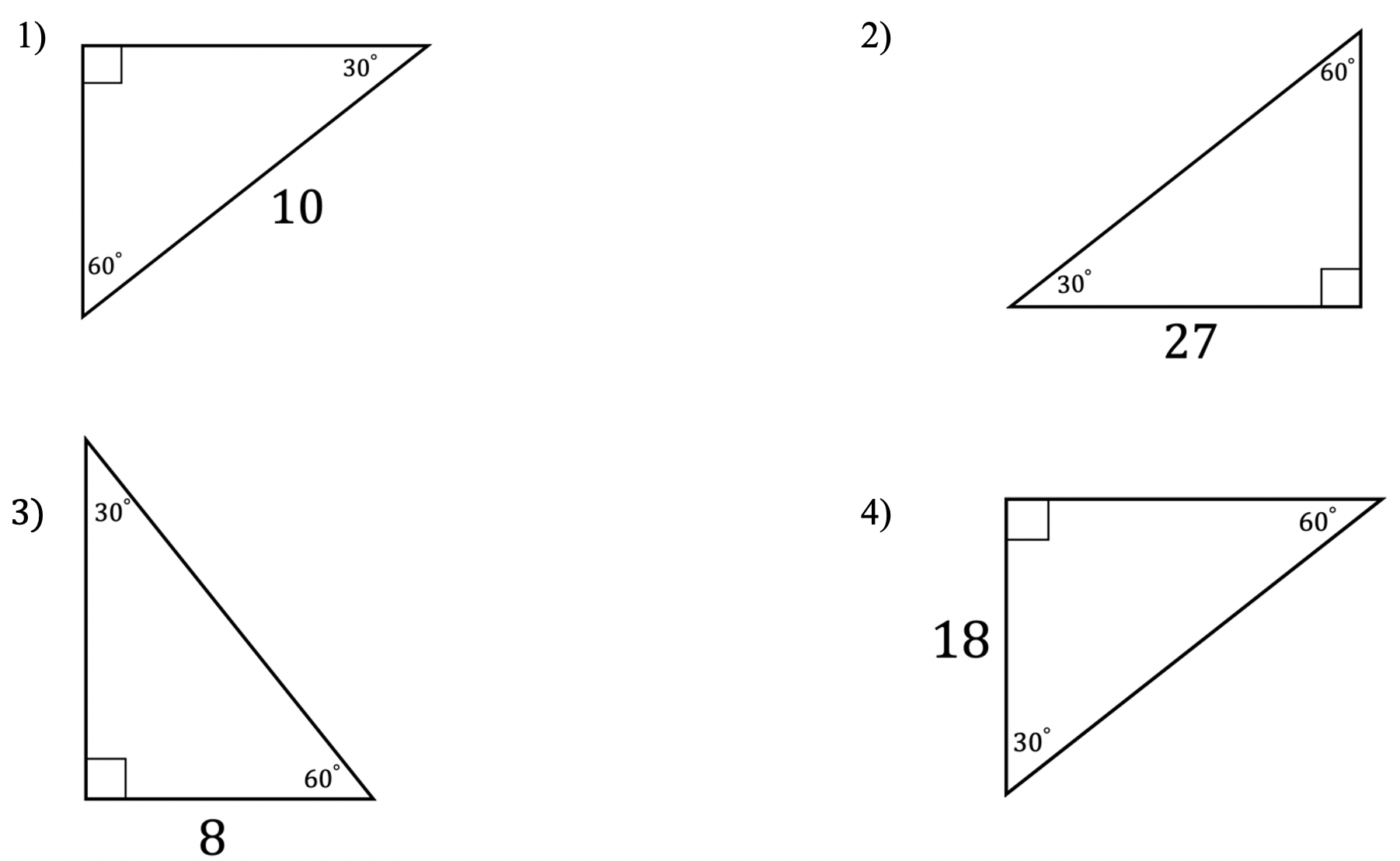
Solutions:
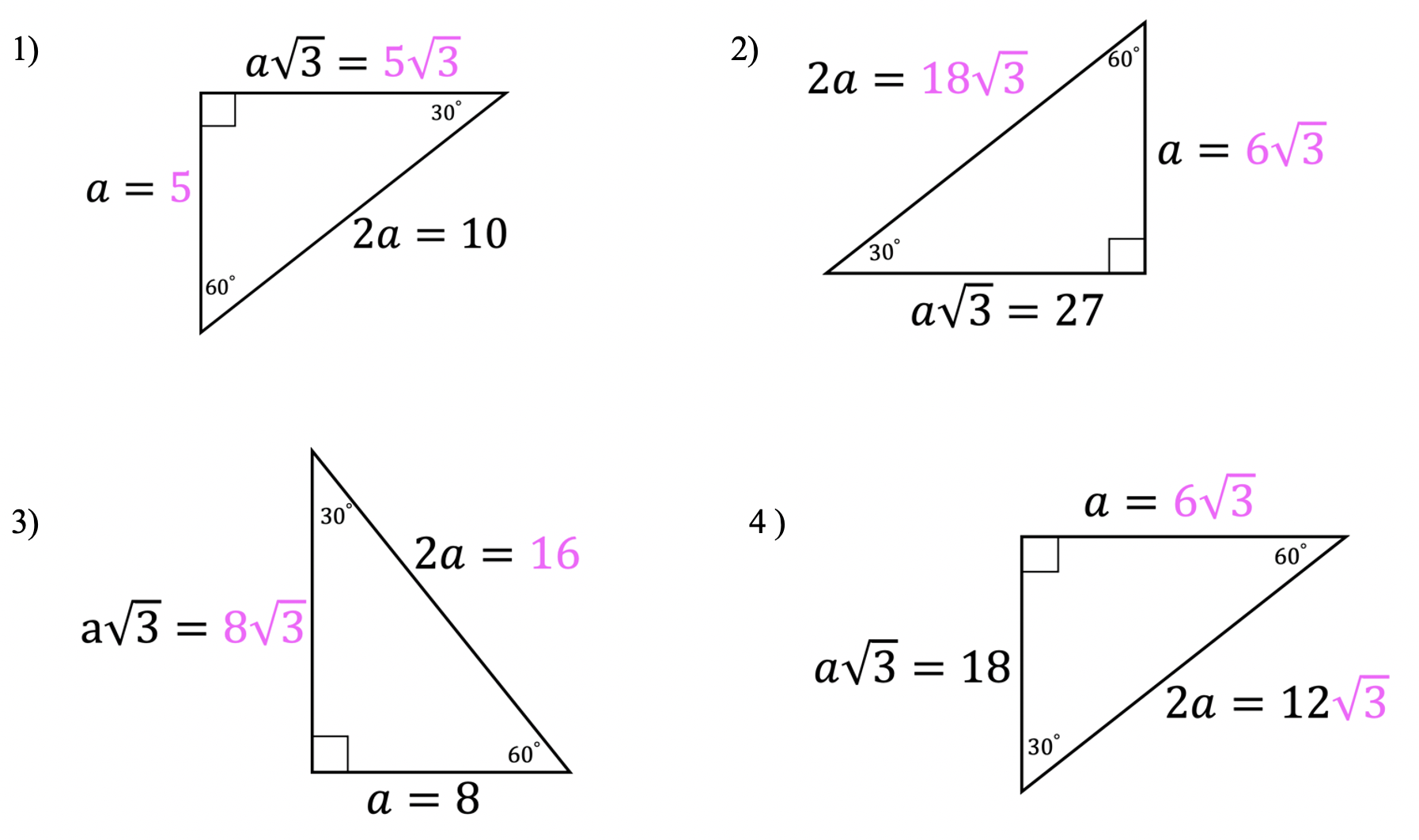
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Related Trigonometry Posts:
Basic Right Triangle Trigonometric Ratios (SOH CAH TOA)
Factoring Trigonometric Functions
