Greetings math friends! In today’s post we’re going to go over some unit circle basics. We will find the value of trigonometric functions by using the unit circle and our knowledge of special triangles. For even more practice questions and detailed info., don’t forget to check out the video and examples at the end of this post. Keep learning and happy calculating! 🙂
What is the Unit Circle?
The Unit Circle is a circle where each point is 1 unit away from the origin (0,0). We use it as a reference to help us find the value of trigonometric functions.
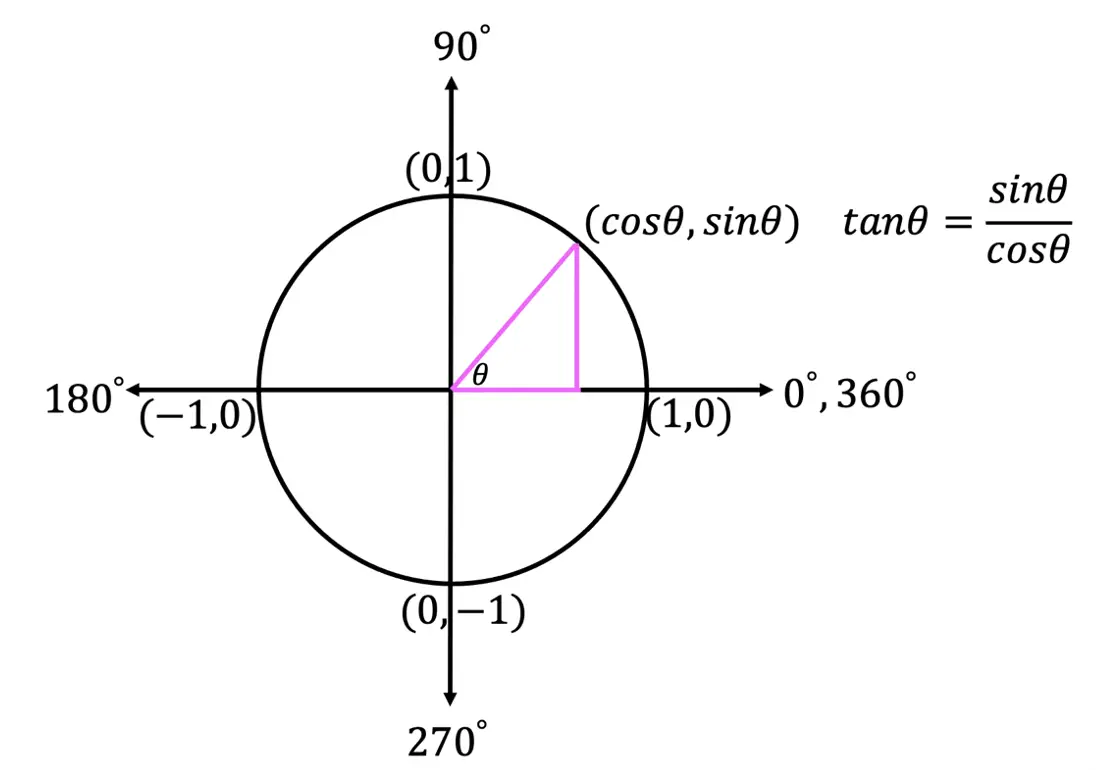
Notice the following things about the unit circle above:
- Degrees follow a counter-clockwise pattern from 0 to 360 degrees.
- Values of cosine are represented by x-coordinates.
- Values of sine are represented by y-coordinates.
- Using the unit circle we can find the degree and radian value of trigonometric functions (SOH CAH TOA). Check out the example below!
What’s the big deal with Quadrants?
Within a coordinate plane there are 4 quadrants numbered I, II, III, and IV used throughout all of mathematics. Within these quadrants there are different trigonometric functions that are positive to each unique quadrant. This will be important when solving questions with reference angles later in this post. Check out which trig functions are positive in each quadrant below:

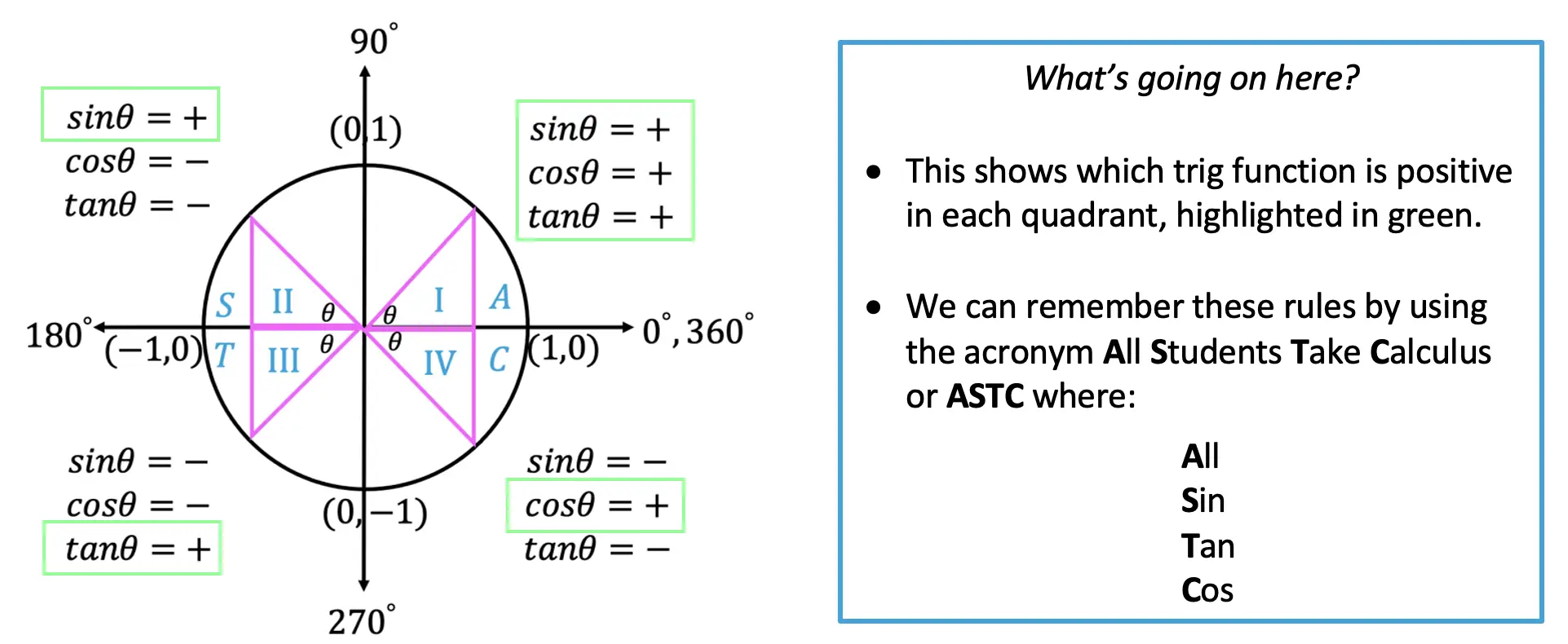
Now let’s look at some examples on how to find trigonometric functions using our circle!

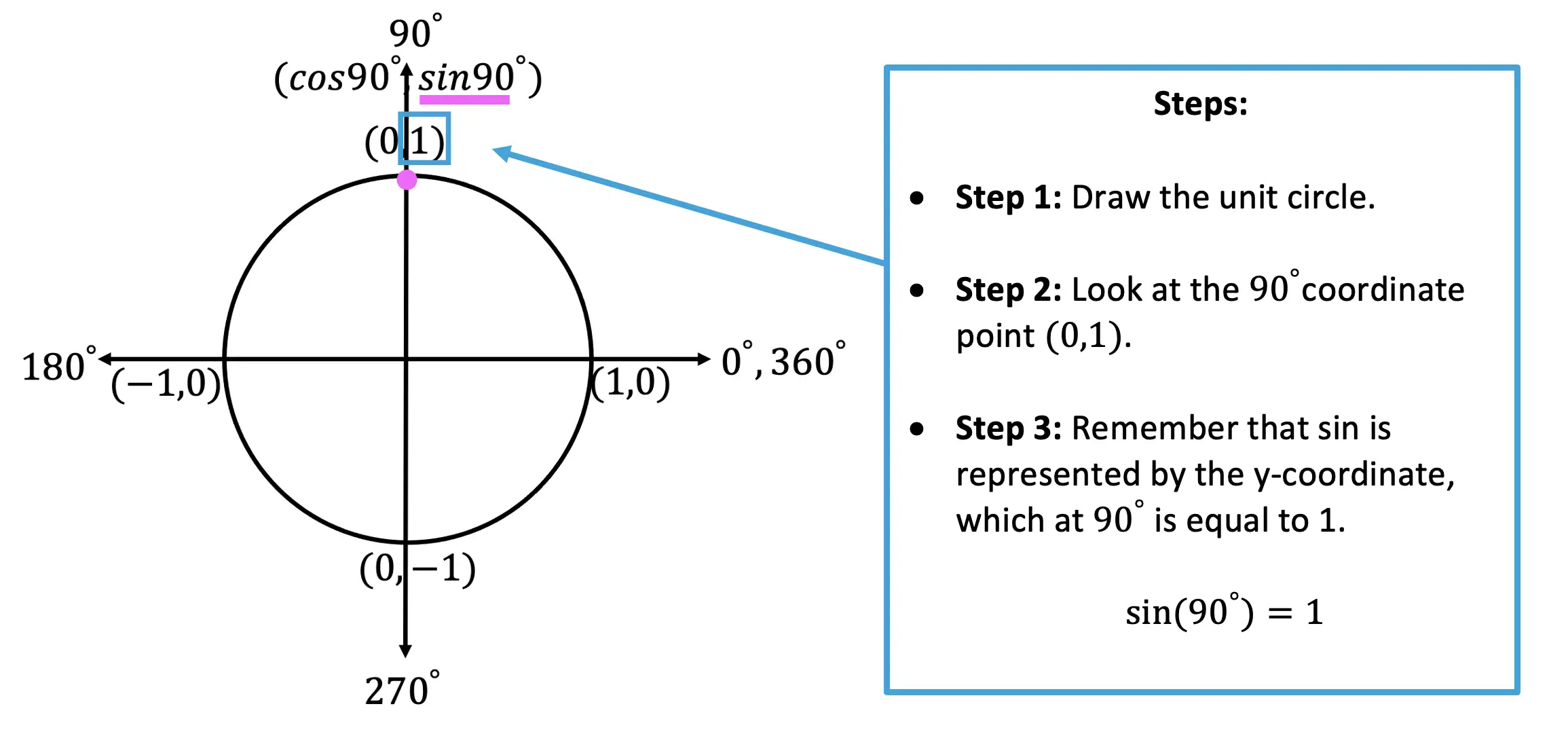
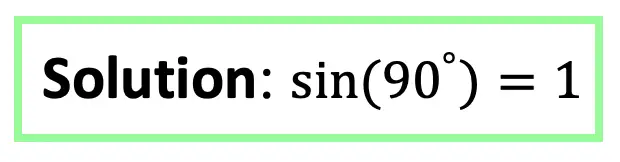
Negative Degree Values:
The unit circle also allows us to find negative degree values which run clockwise, check it out below!
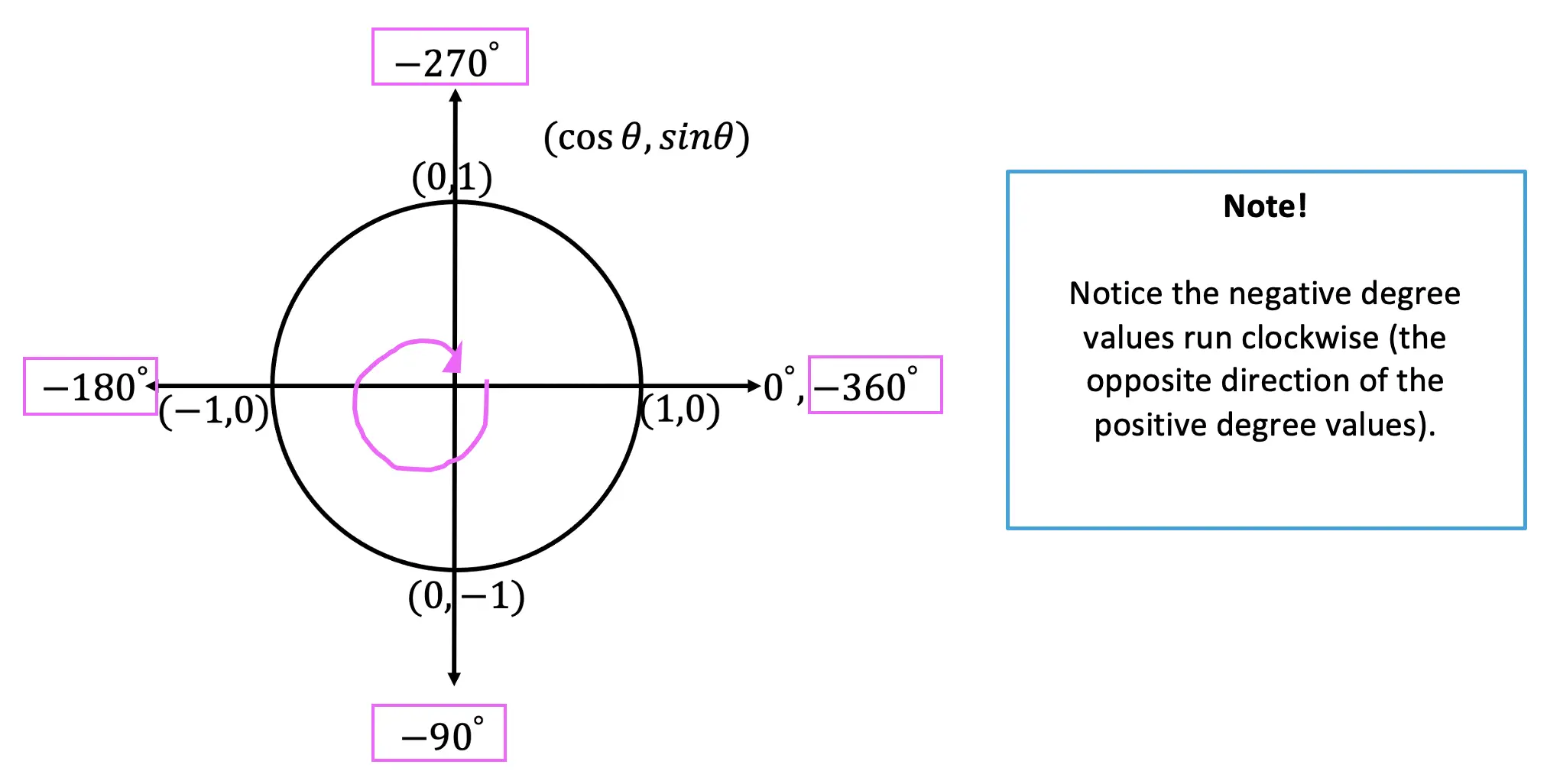
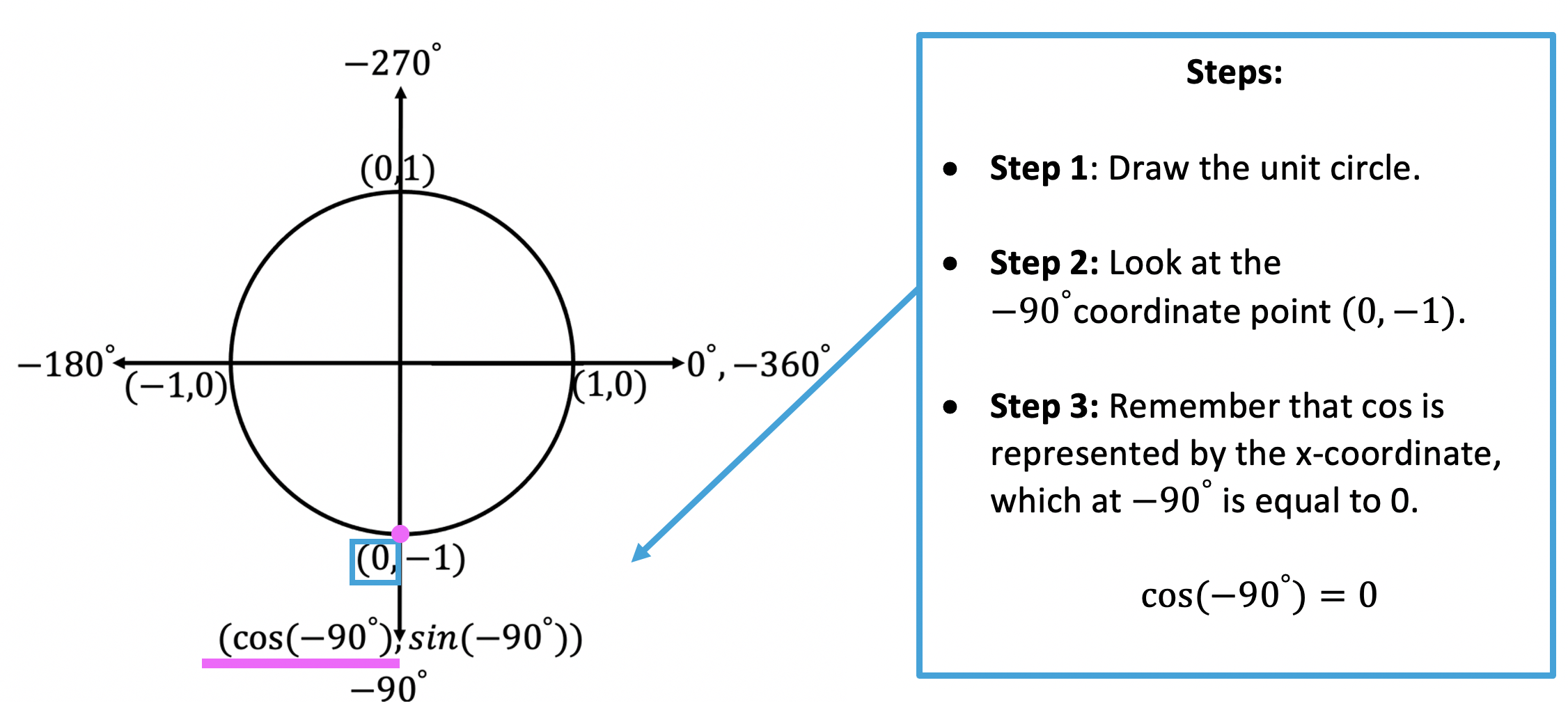
Knowing that negative degrees run clockwise, we can now find the value of trigonometric functions with negative degree values.

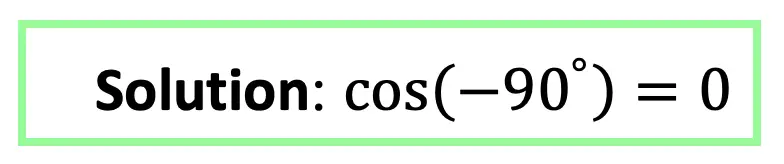
How to find trig ratios with 30º, 45º and 60º ?
Instead of memorizing much, much more of the unit circle, there’s a trick to memorizing two simple special triangles for answering these types of questions. The 45º 45º 90º special triangle and the 30º 60º 90º special triangle. (Why does this work? These special triangles can also be derived and found on the unit circle).
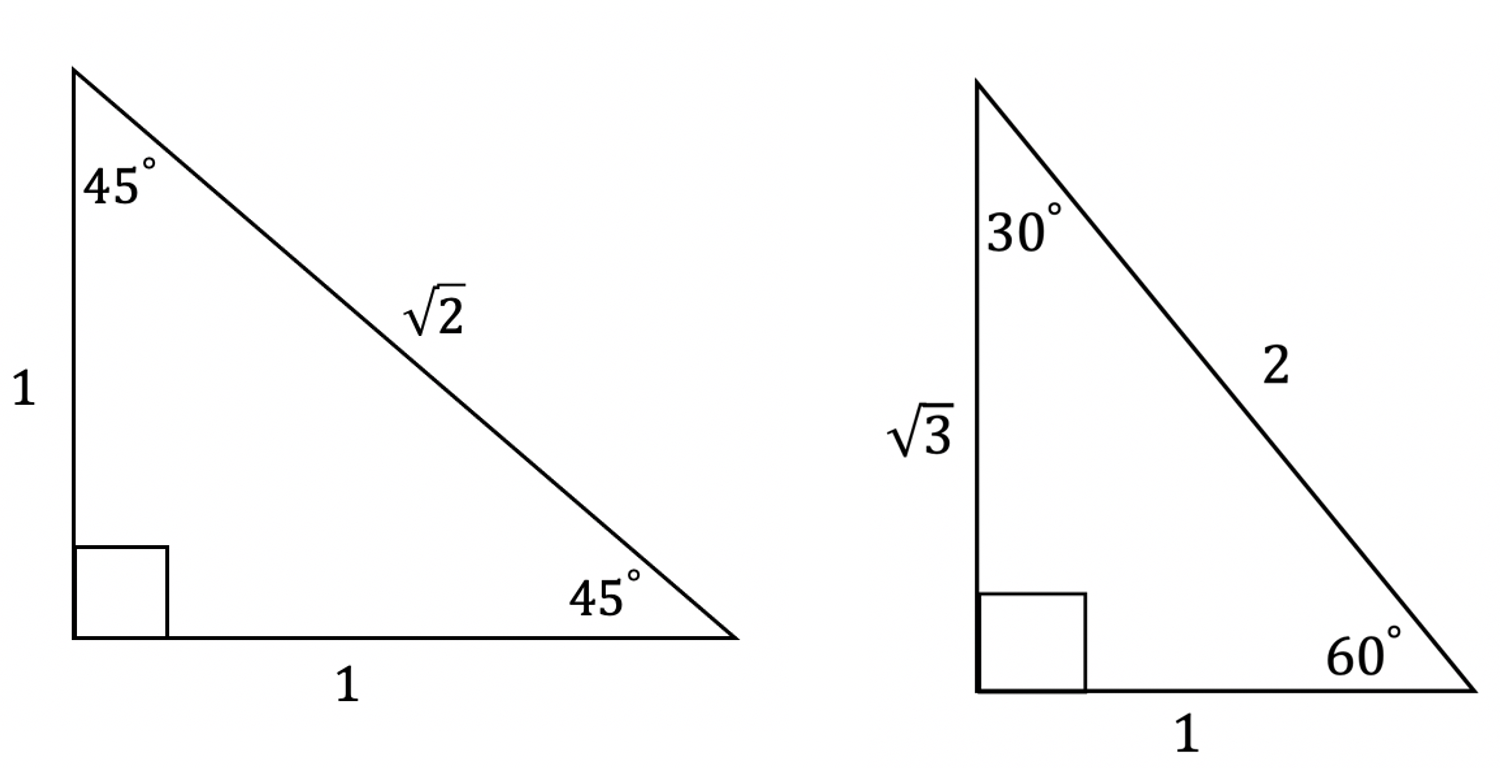
Using the above triangles and some basic trigonometry in conjugation with the unit circle, we can find so many more angles, take a look at the example below:

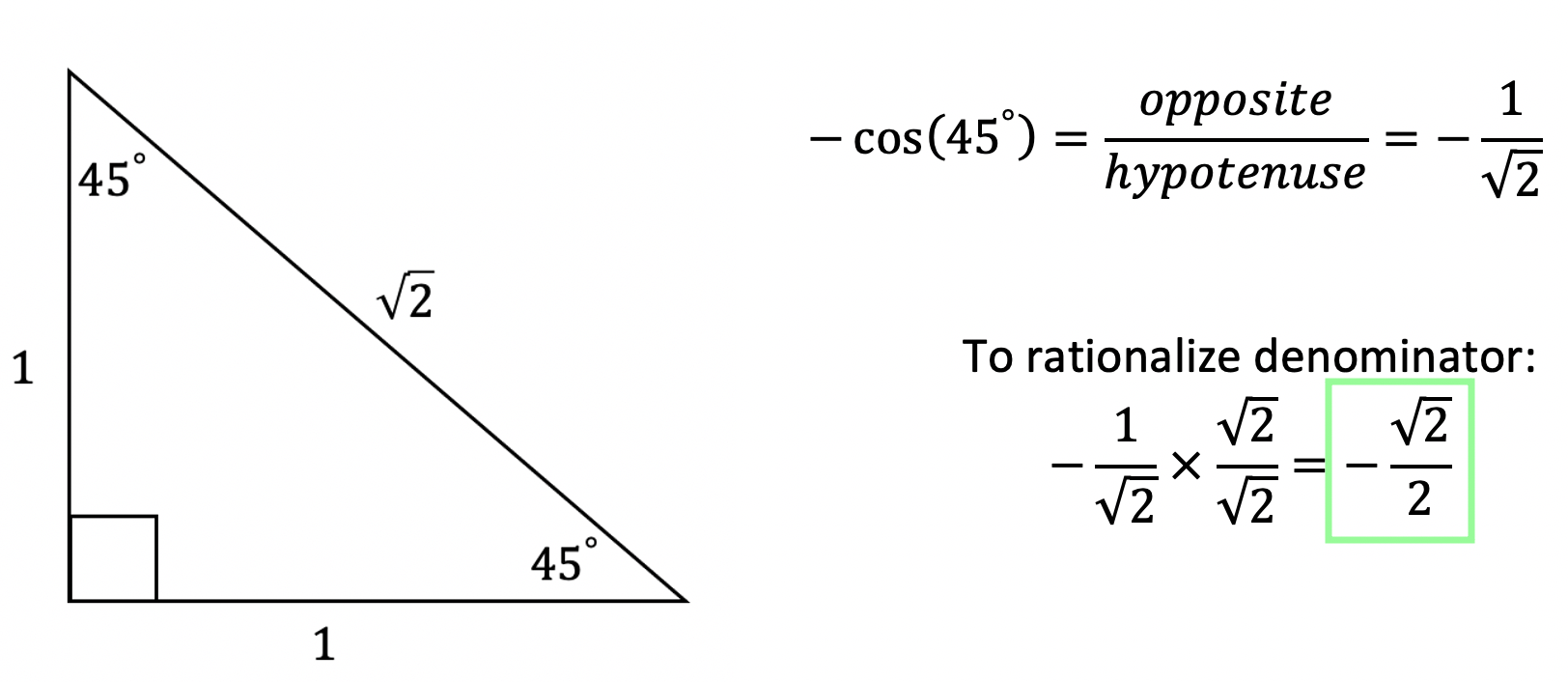
Since we need to find the value of tan(45º) , we will use the 45º, 45º, 90º special triangle.
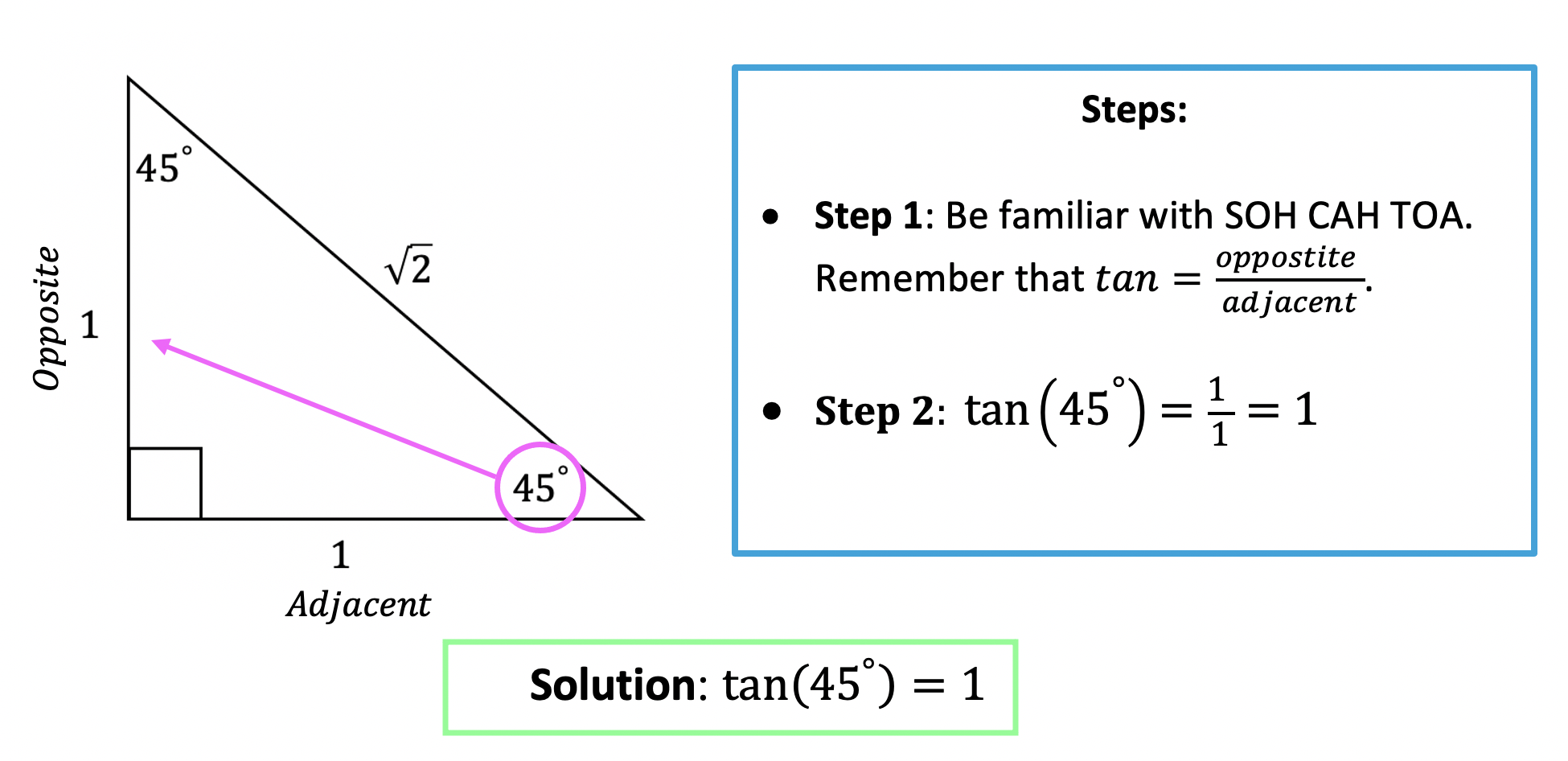
For our last question, we are going to need to combine our knowledge of unit circles and special triangles:

-> In order to do this, we must first look at where our angle falls on the unit circle. Notice that the angle 135º is encompassed by the pink lines and falls in quadrant 2.
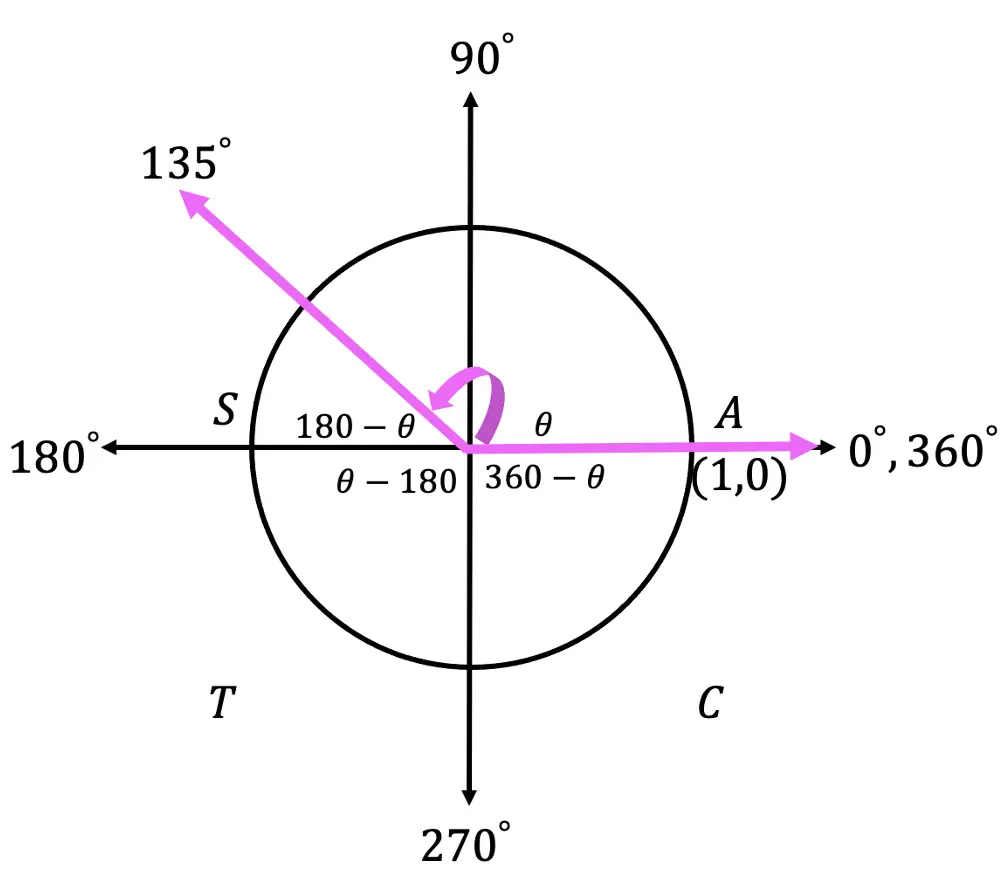
-> Since our angle falls in the second quadrant where only the trig function sin is positive. Since we are finding an angle with the function cosine, we know the solution will be negative.
-> Now we need to find something called a reference angle. Which is what those θ, 180°-θ, θ-180°, 360°-θ and symbols represent towards the center of the unit circle. Using these symbols will help us find the value of cos(135º).
Because the angle we are trying to find,135º , falls in the second quadrant, that means we are going to use the reference angle that falls in that quadrant 180º-θ theta, using the angle we are given as θ.
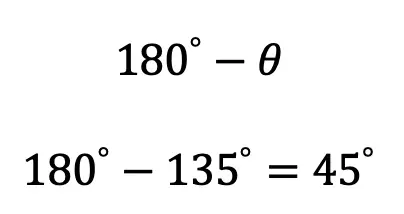
-> Now we can re-write and solve our trig equations using our newly found reference angle, 45º.
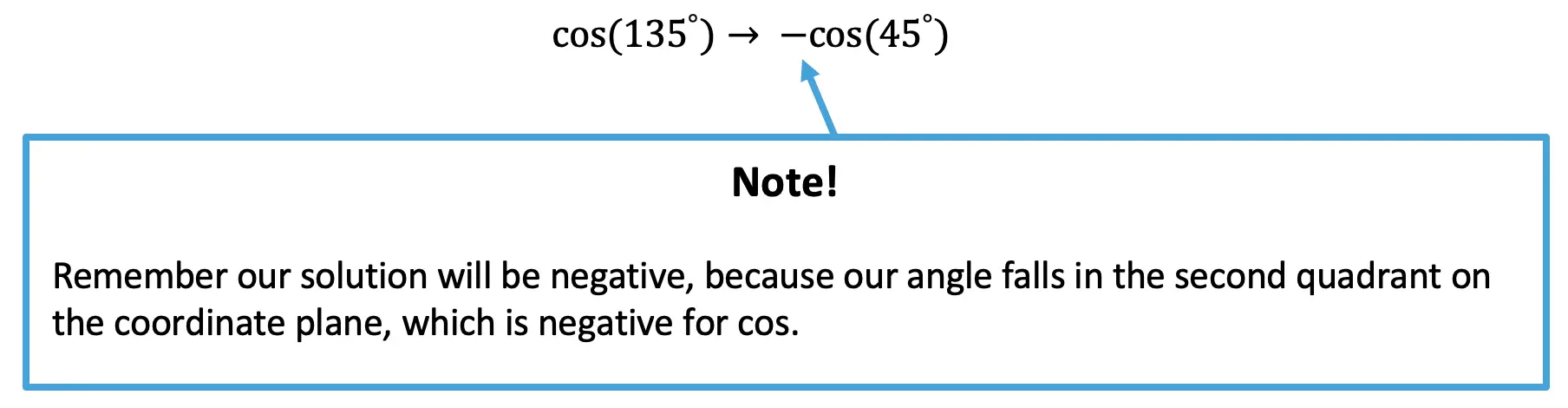
Now we are going to use our 45º 45º 90º special triangle and SOH CAH TOA to evaluate our trig function. For a review on how to use SOH CAH TOA, check out this link here.
When you’re ready, try the problems on your own below!
Practice Questions:
Solve the following trig functions using a unit circle and your knowledge of special triangles:
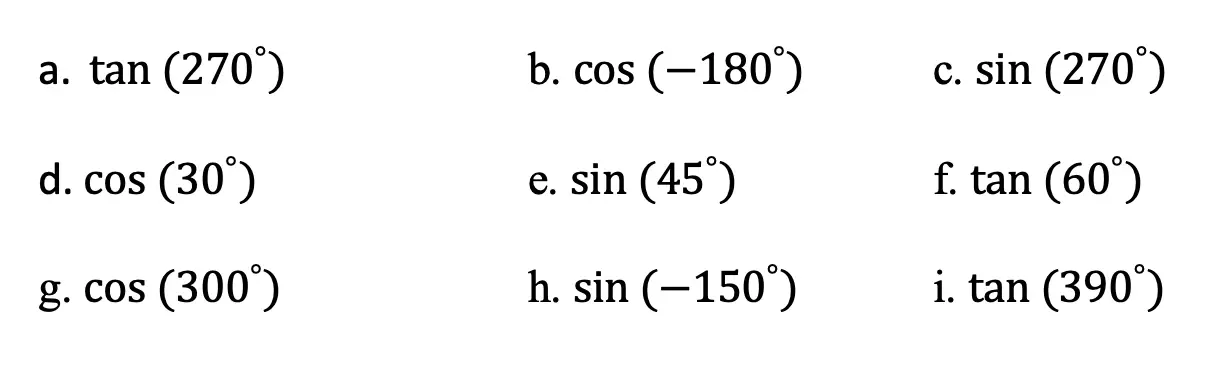
Solutions:
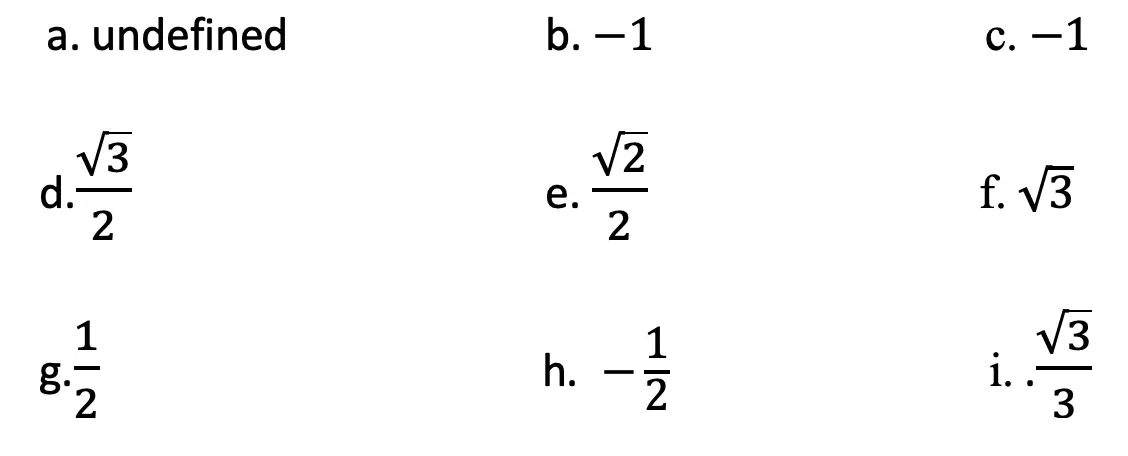
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above for even more examples. Happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Related Trigonometry Posts:
Basic Right Triangle Trigonometric Ratios (SOH CAH TOA)
