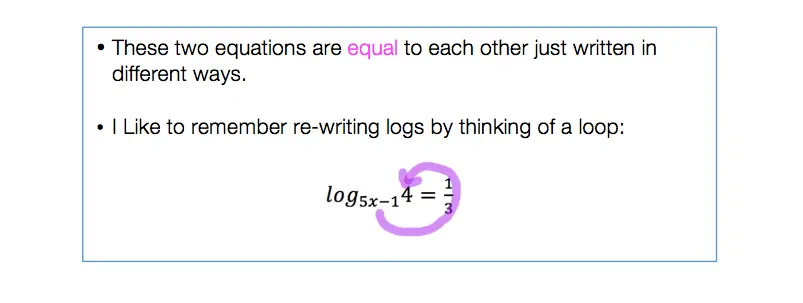
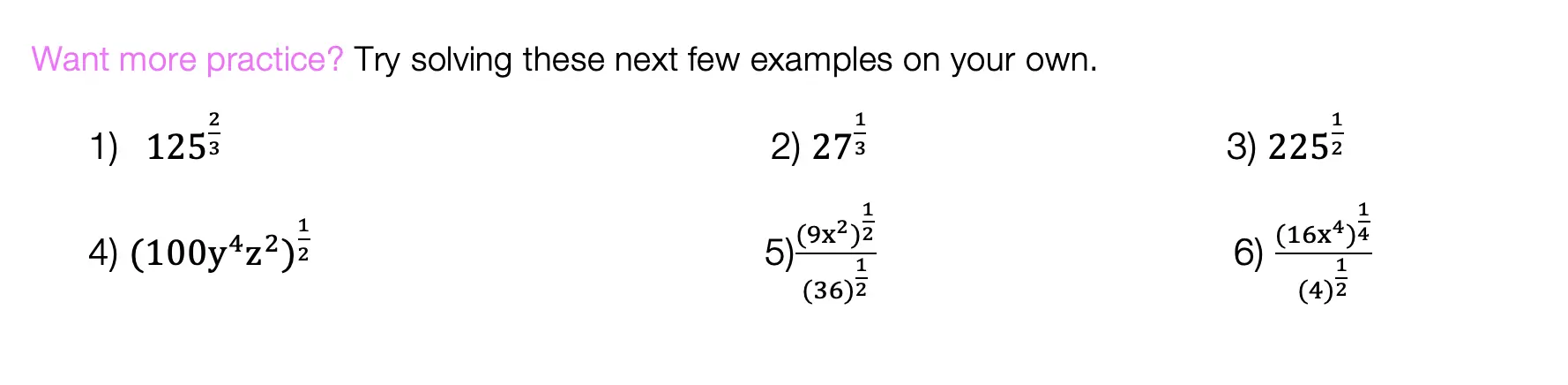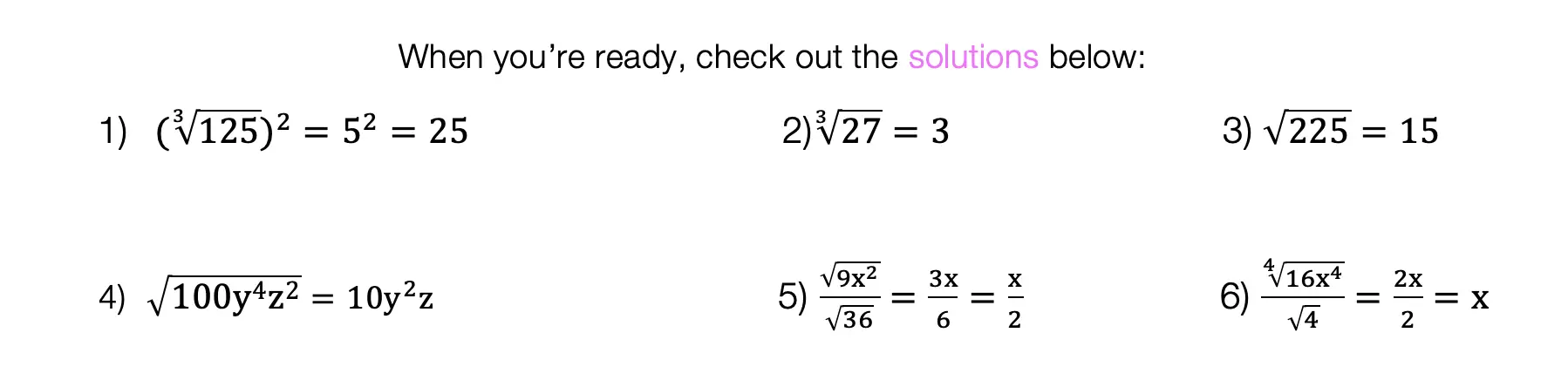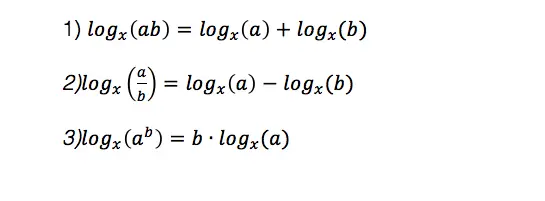Happy Wednesday and back to school season math friends! This post introduces imaginary and complex numbers when raised to any power exponent and when multiplied together as a binomial. When it comes to all types of learners, we got you between the video, blog post, and practice problems below. Happy calculating! 🙂
What are Imaginary Numbers?
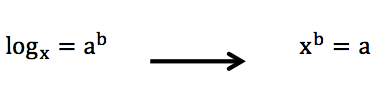
Imaginary numbers happen when there is a negative under a radical and looks something like this:
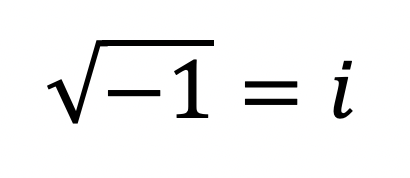
Why does this work?
In math, we cannot have a negative under a radical because the number under the square root represents a number times itself, which will always give us a positive number.
Example:


But wait, there’s more:
When raised to a power, imaginary numbers can have the following different values:

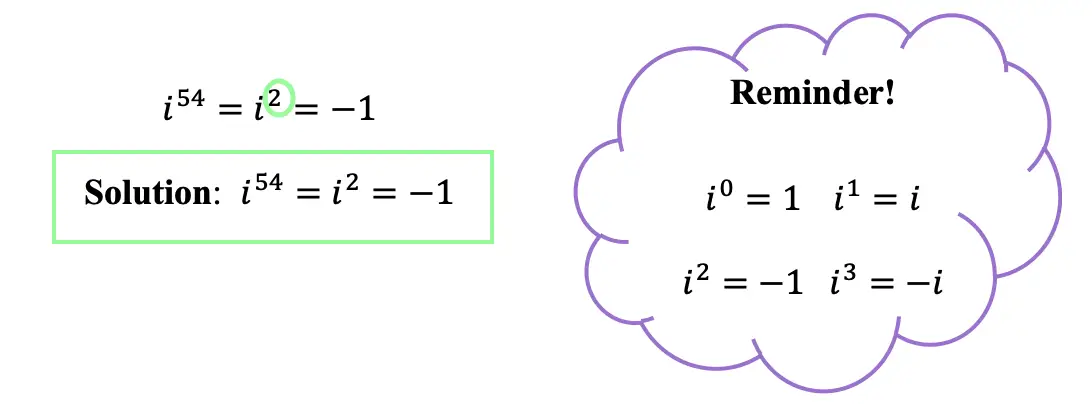
Knowing these rules, we can evaluate imaginary numbers, that are raised to any value exponent! Take a look below:

-> We use long division, and divide our exponent value 54, by 4.

-> Now take the value of the remainder, which is 2, and replace our original exponent. Then evaluate the new value of the exponent based on our rules.
What are Complex Numbers?
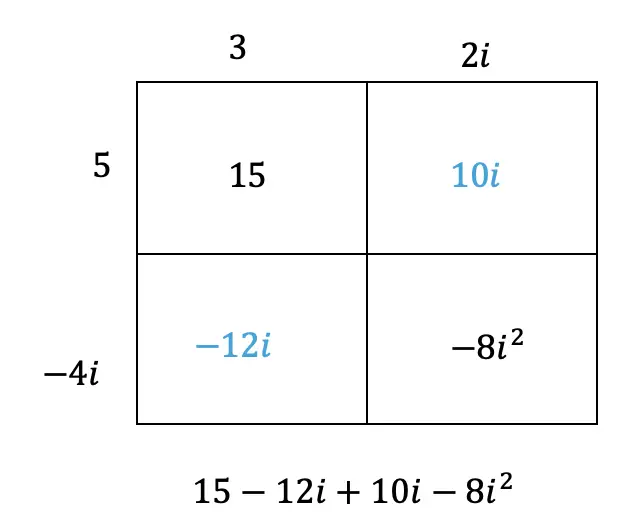
Complex numbers combine imaginary numbers and real numbers within one expression in a+bi form. For example, (3+2i) is a complex number. Let’s evaluate a binomial multiplying two complex numbers together and see what happens:

-> There are several ways to multiply these complex numbers together. To make it easy, I’m going to show the Box method below:


Try mastering imaginary and complex numbers on your own with the questions below!
Practice:
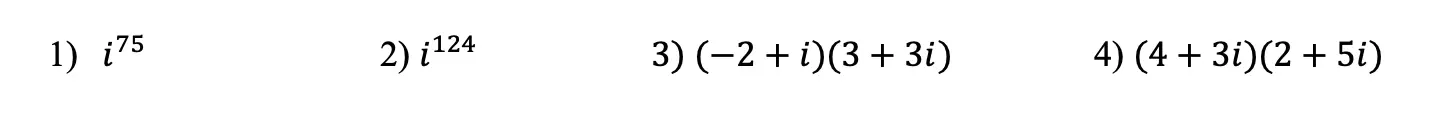
Solutions:
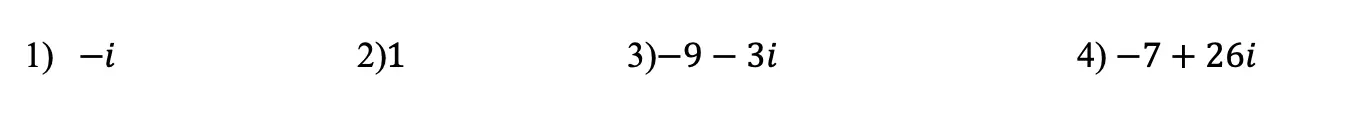
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Don’t forget to sign up for FREE weekly MathSux videos, lessons, and practice questions. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Also, if you’re looking to learn more about dividing polynomials, check out this post here!
Looking for more on Quadratic Equations and functions? Check out the following Related posts!
Focus and Directrix of a Parabola
Quadratic Equations with 2 Imaginary Solutions