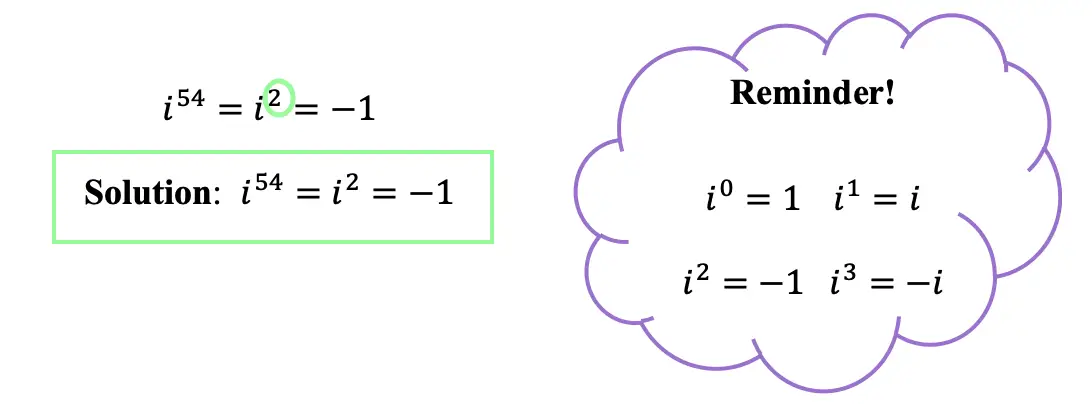
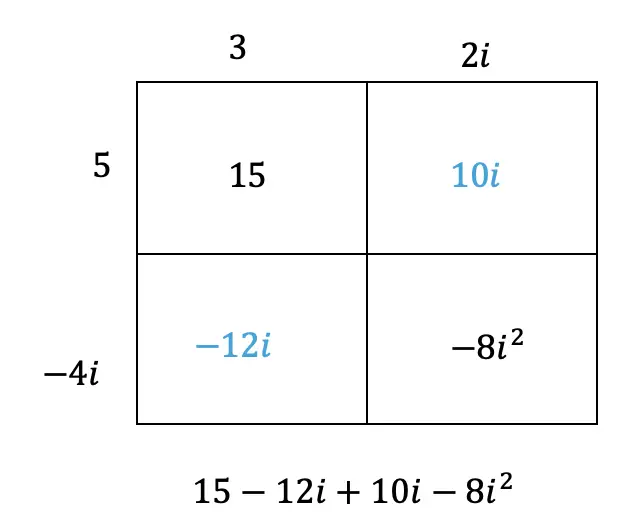
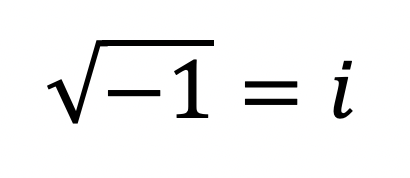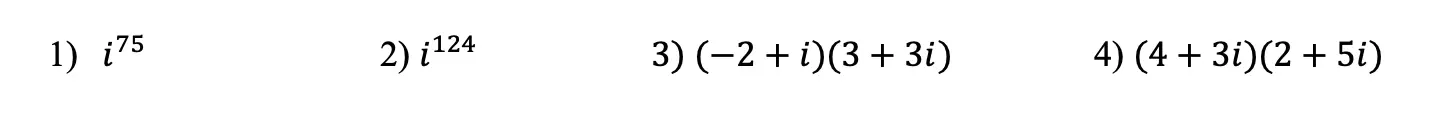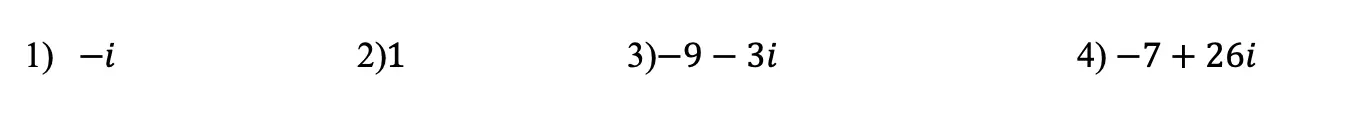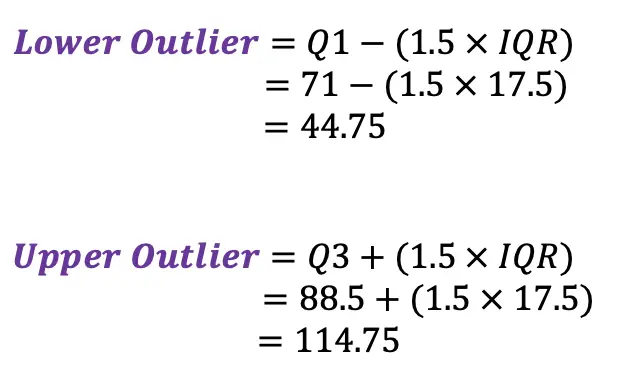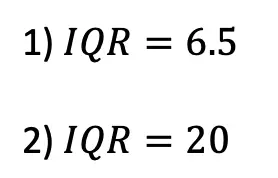math tutor Archives - Page 3 of 3

Transversals and Parallel Lines: Geometry

Happy Wednesday math friends! In this post we are going to look at transversals and parallel lines and find the oh so many congruent and supplementary angles they form when they come together! Congruent angles that form with these types of lines are more commonly known as Alternate Interior Angles, Alternate Exterior Angles, Corresponding angles, and Supplementary angles. Let’s look at this one step at a time:

What are Transversals and Parallel Lines?

When two parallel lines are cut by a diagonal line ( called a transversal) it looks something like this:

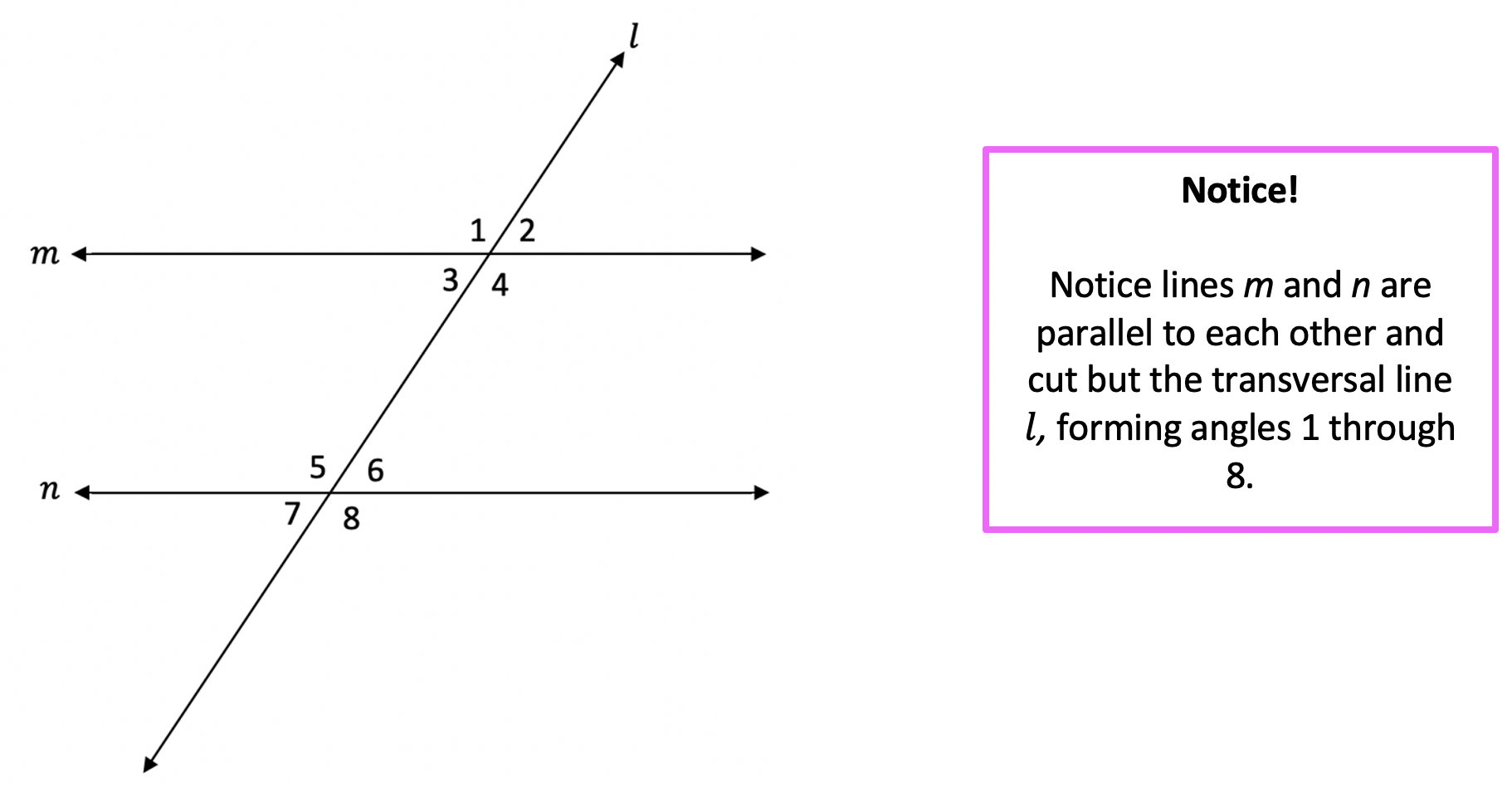
Each angle above has at least one congruent counterpart. There are several different types of congruent relationships that happen when a transversal cuts two parallel lines and we are going to break each down:

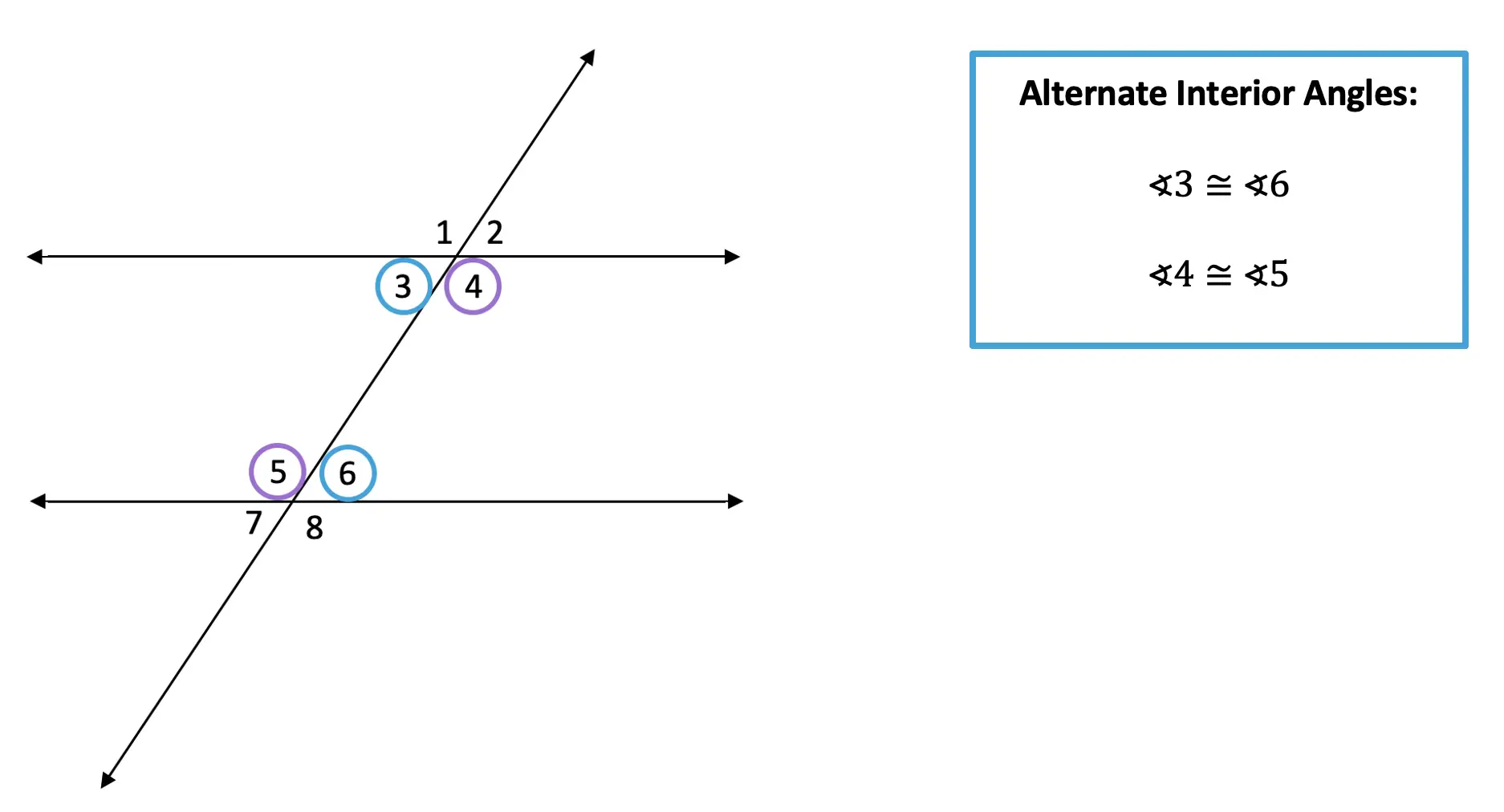
1) Alternate Interior Angles:

When a transversal line cuts across two parallel lines, opposite interior angles are congruent.

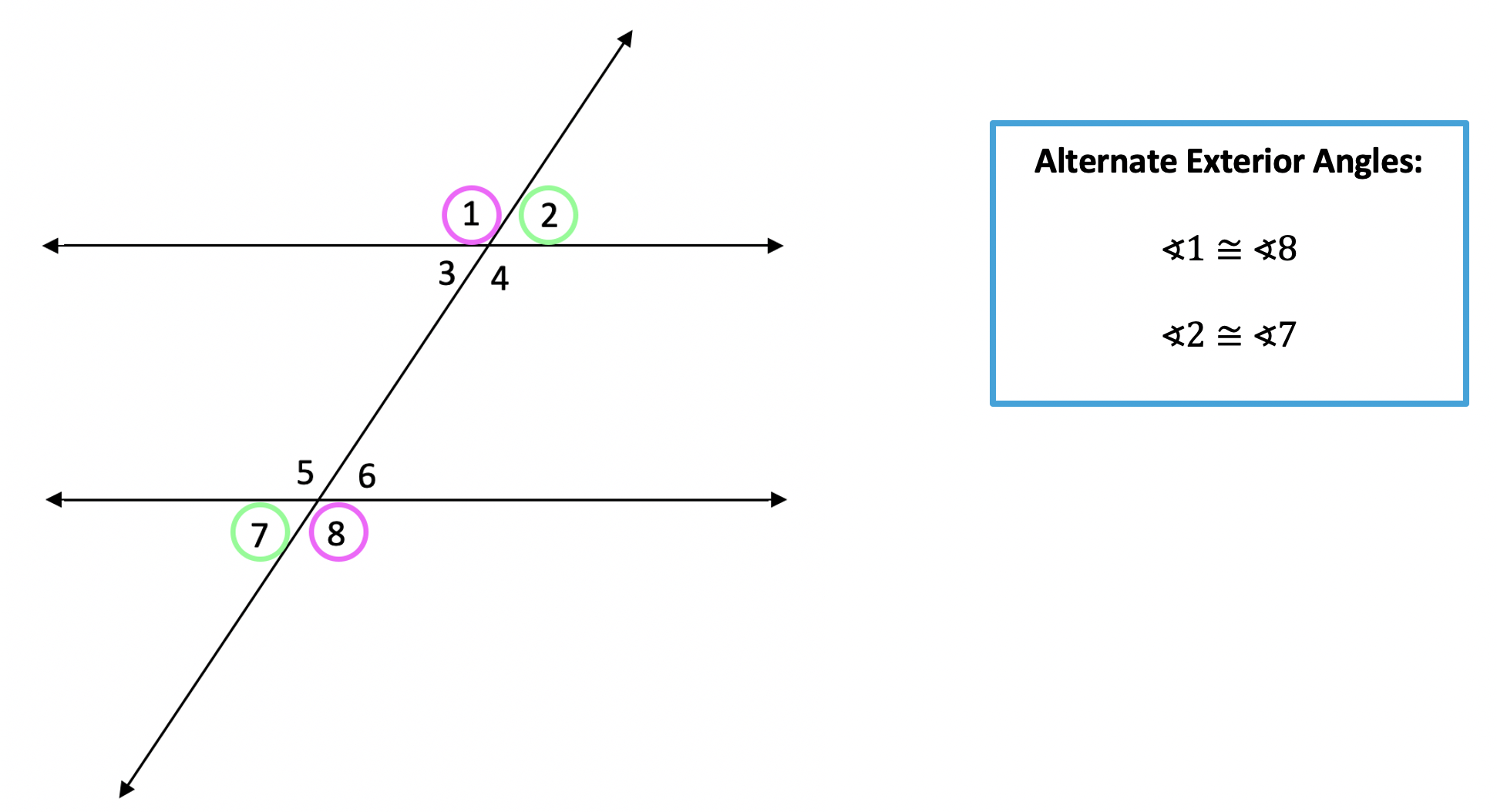
2) Alternate Exterior Angles:

When a transversal line cuts across two parallel lines, opposite exterior angles are congruent.

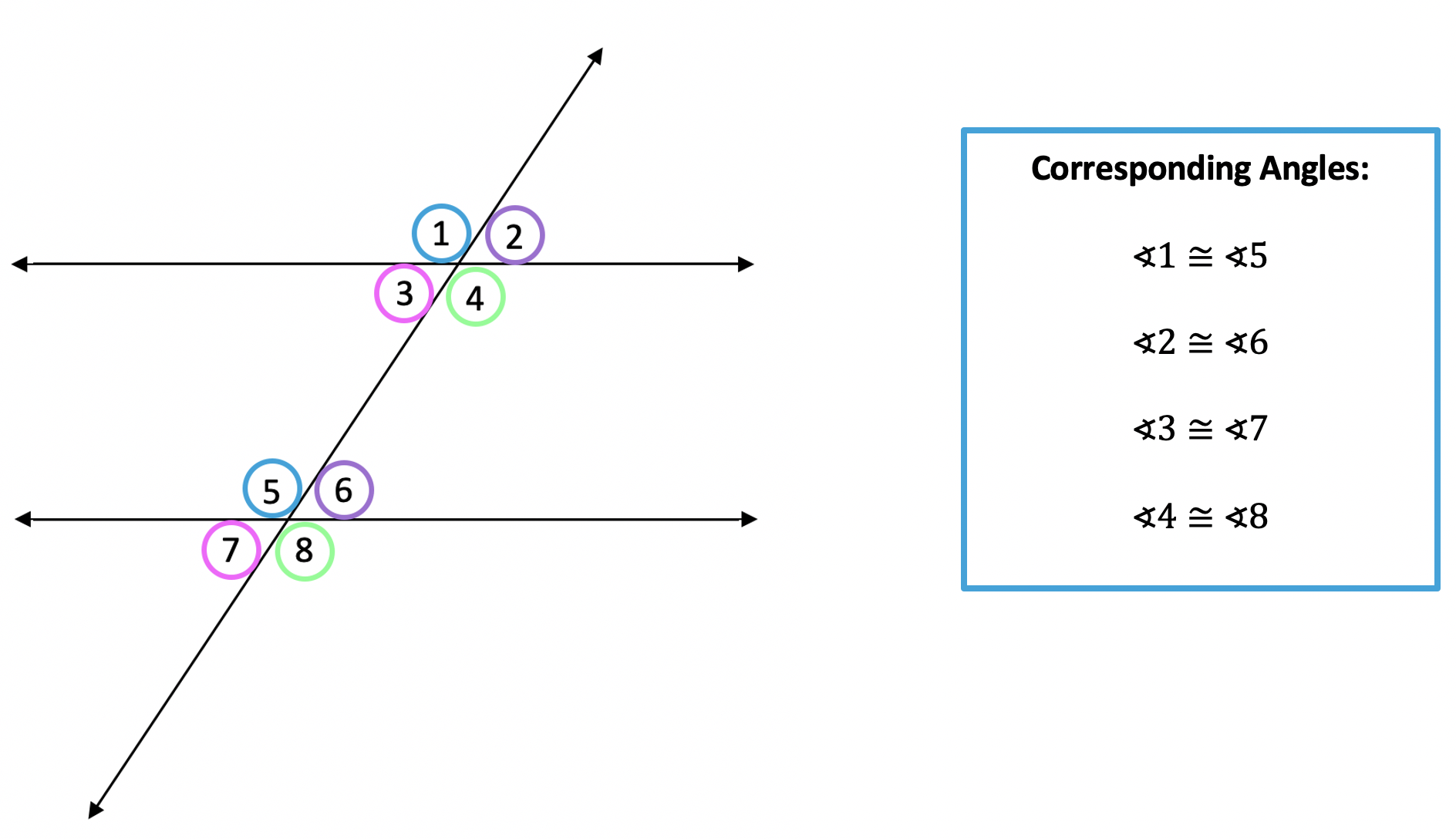
3) Corresponding Angles:

When a transversal line cuts across two parallel lines, corresponding angles are congruent.

4) Supplementary Angles:

Supplementary angles are a pair of angles that add to 180 degrees. 180 degrees is the value of distance found within a straight line, which is why you’ll find so many supplementary angles below:

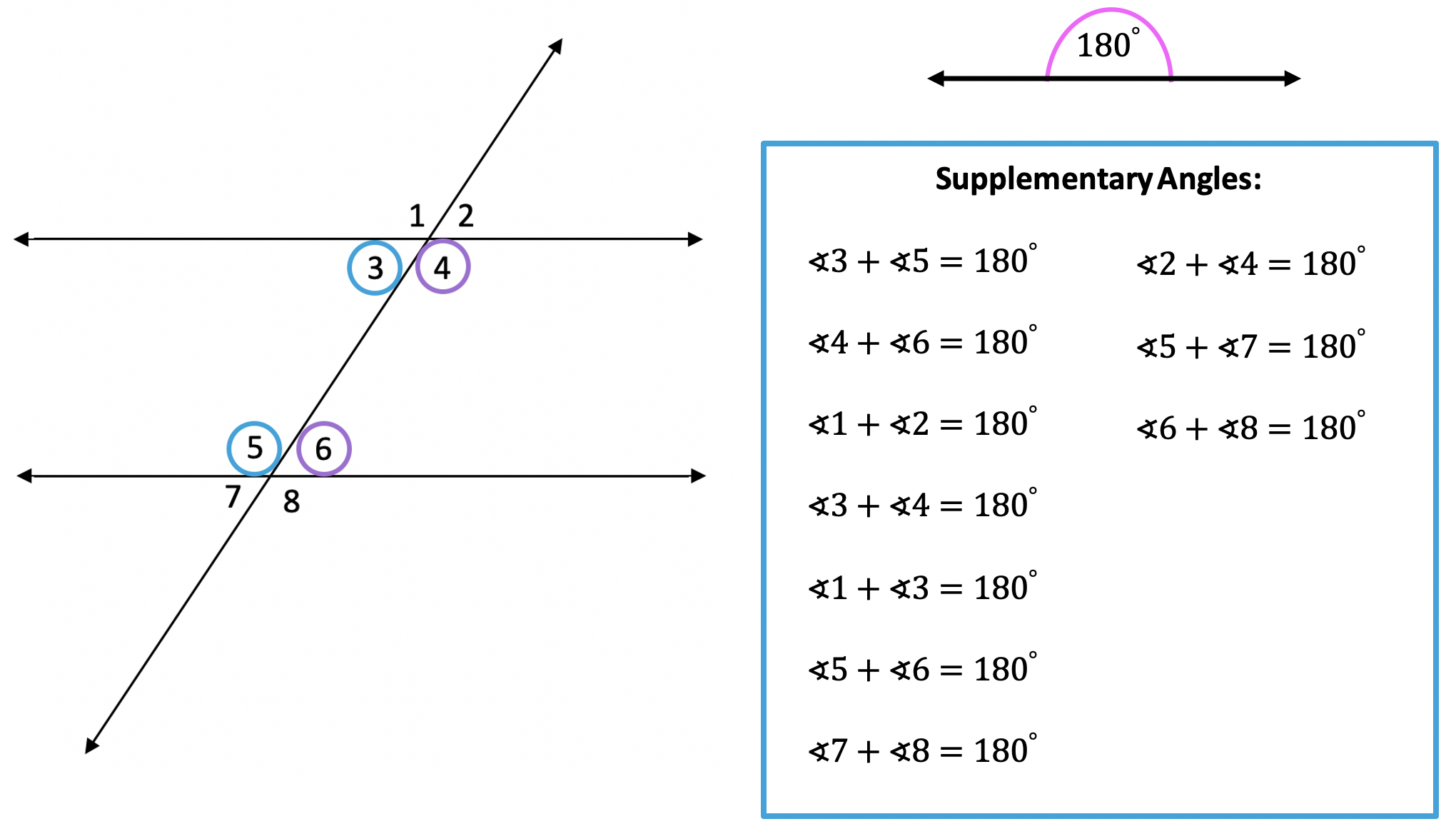
Knowing the different sets of congruent and supplementary angles, we can easily find any missing angle values when faced with the following question:

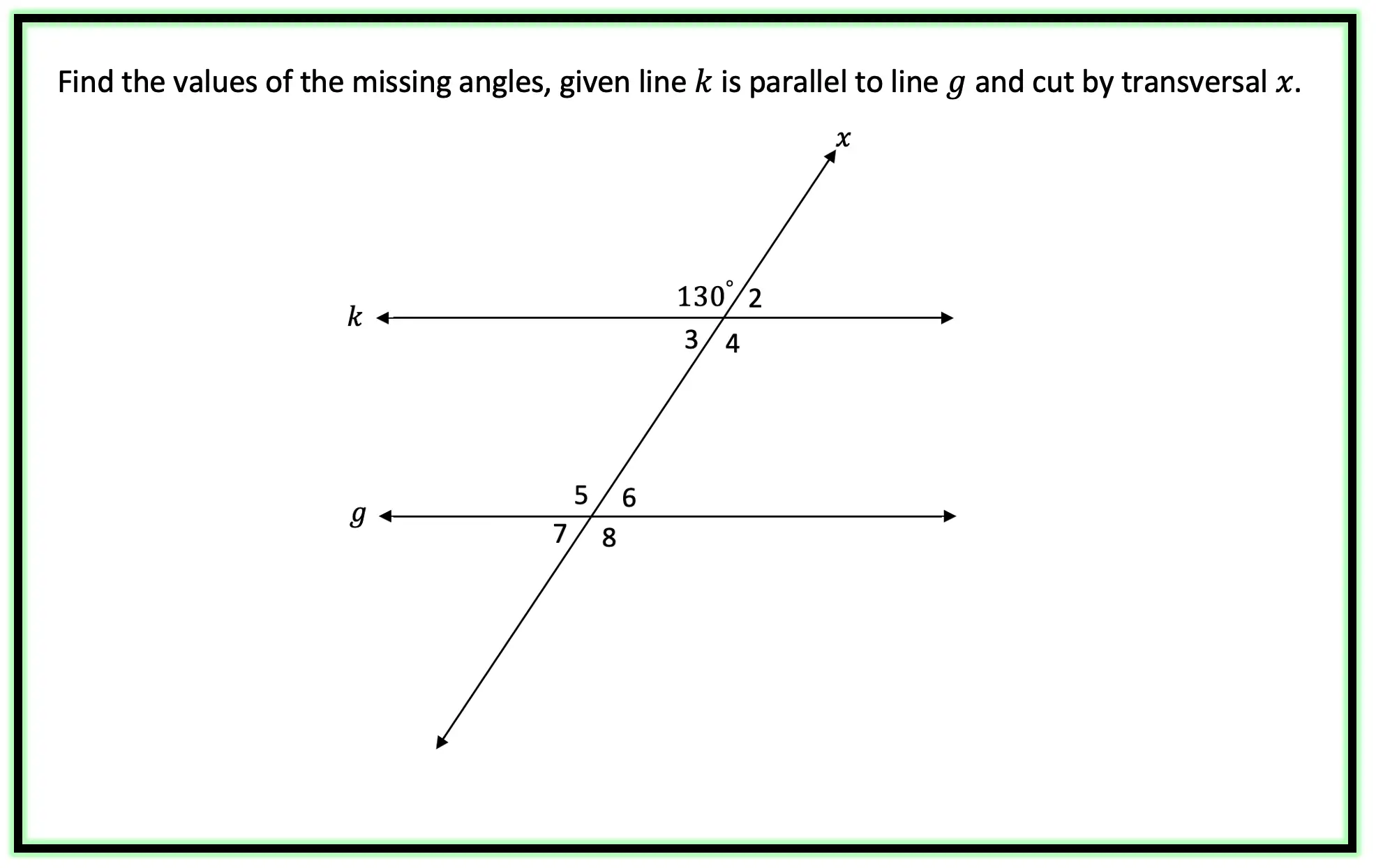
-> Using our knowledge of congruent and supplementary angles we should be able to figure this out! Right away we can find angle 2 by noticing angle 1 and angle 2 are supplementary angles (add to 180 degrees).

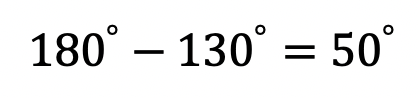
-> Knowing angle 2 is 50 degrees, we can now fill in the rest of our transversal angles based on our corresponding and supplementary rules.

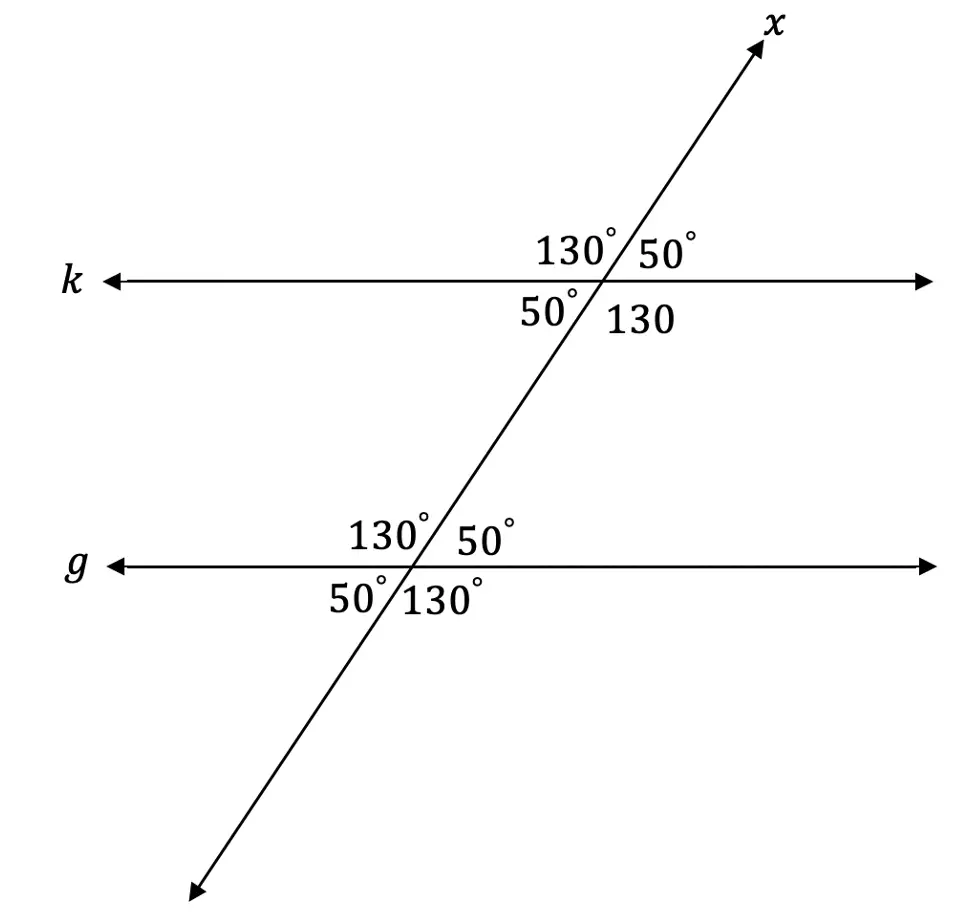
Try the following transversal and parallel lines questions below! Some may a bit harder than the previous example, if you get stuck, check out the video that goes over a similar example above and happy calculating! 🙂

Practice Questions:

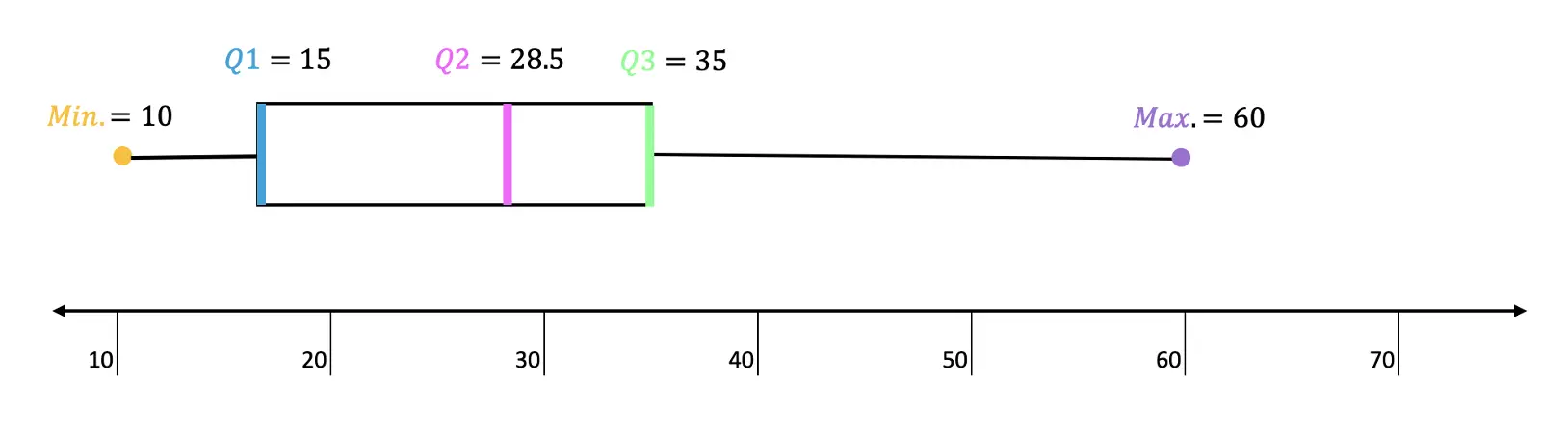
Find the value of the missing angles given line r is parallel to line s and line t is a transversal.

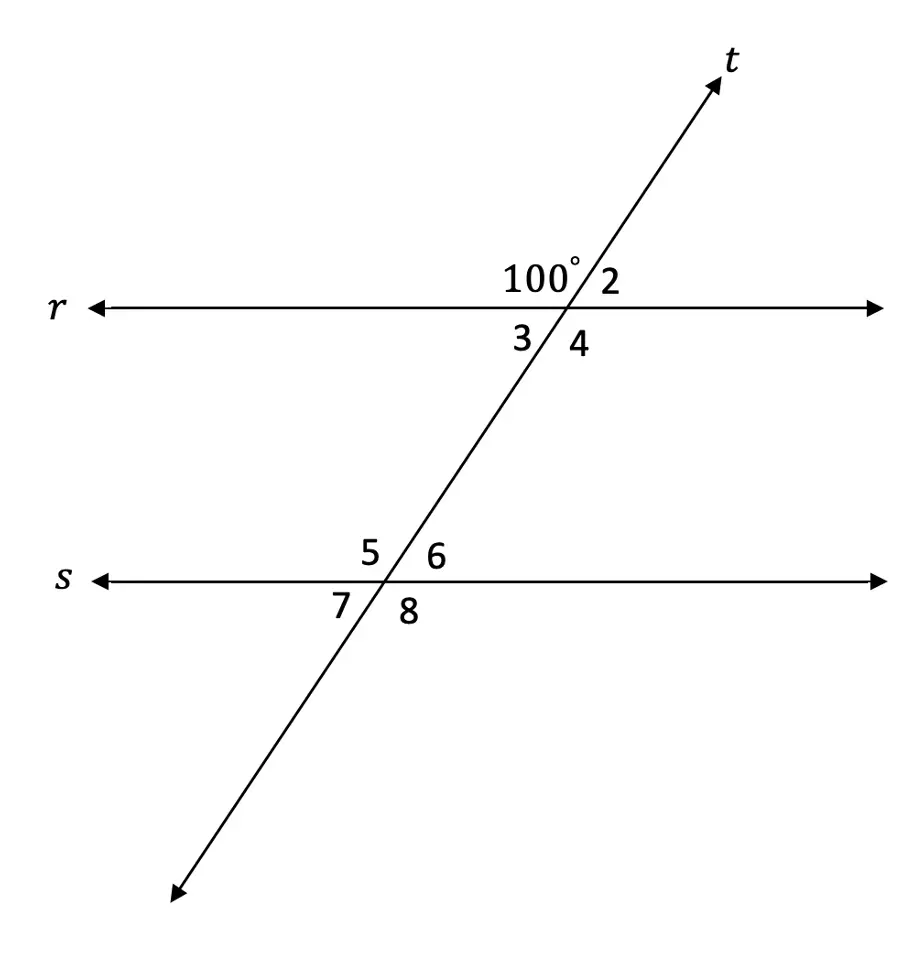
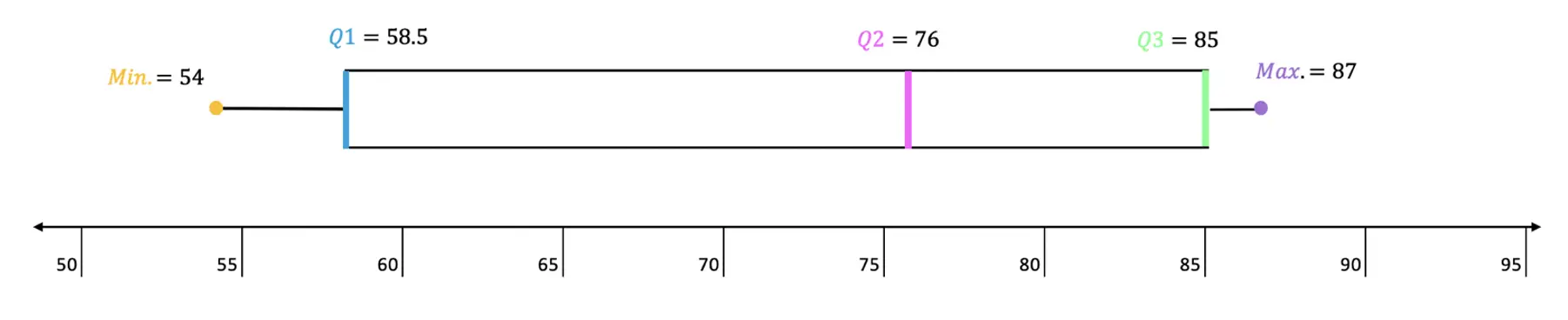
2. Find the value of the missing angles given line r is parallel to line s and line t is a transversal.

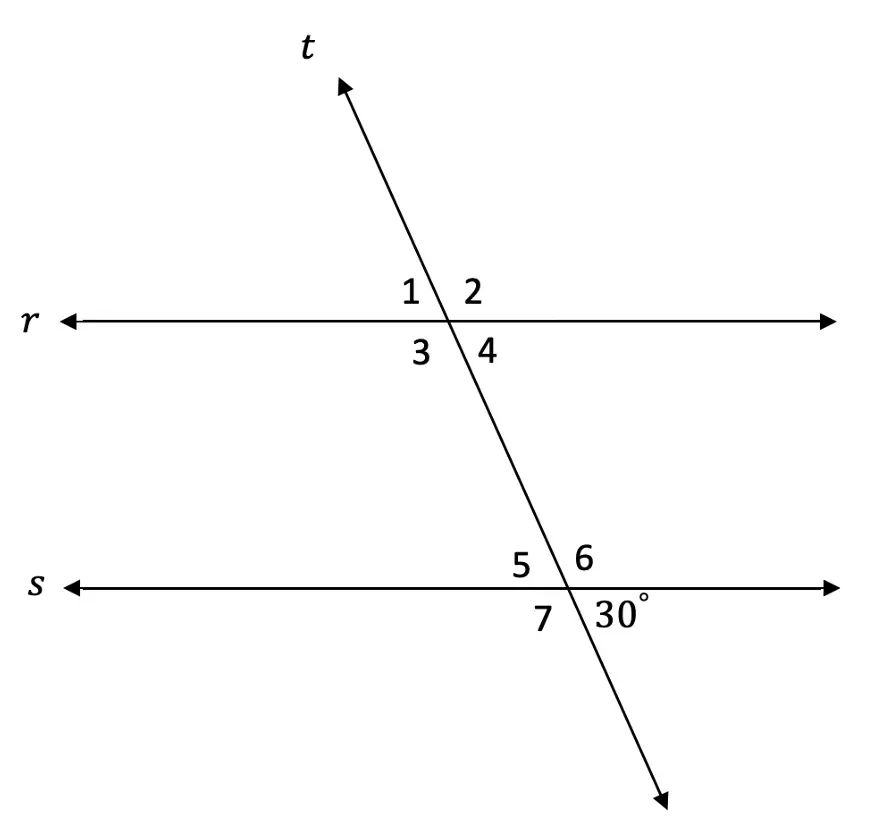
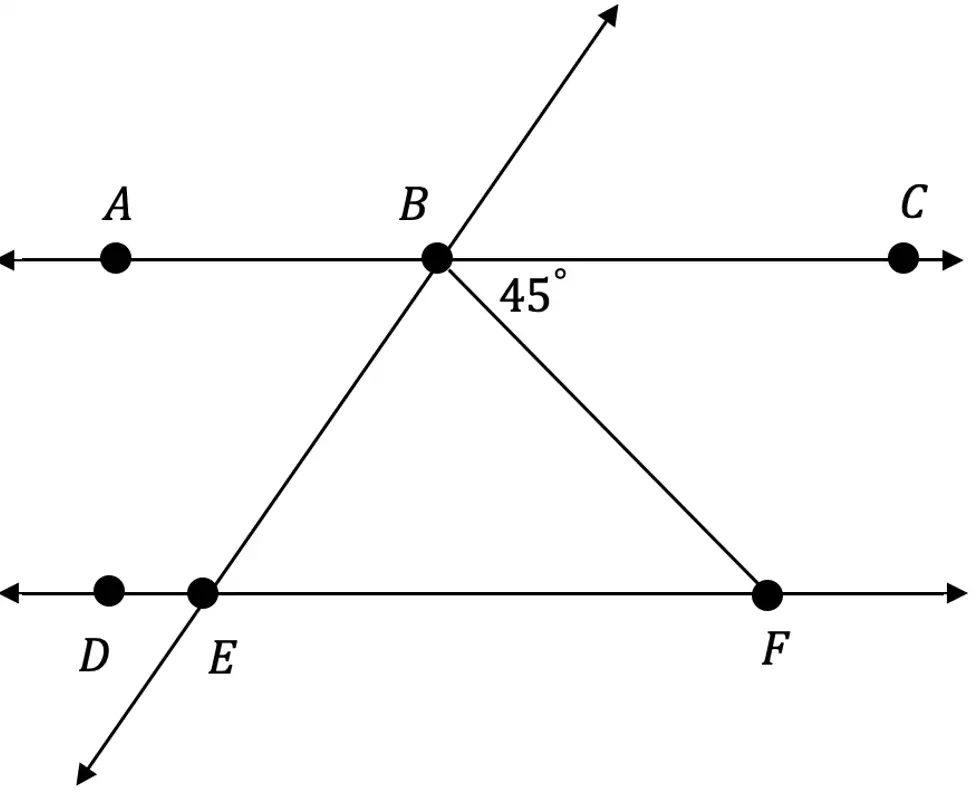
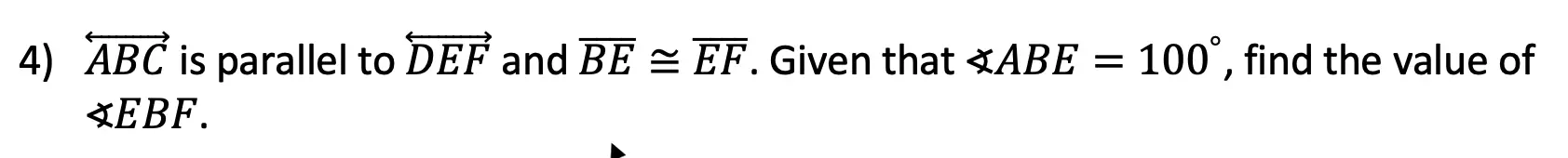
Solutions:

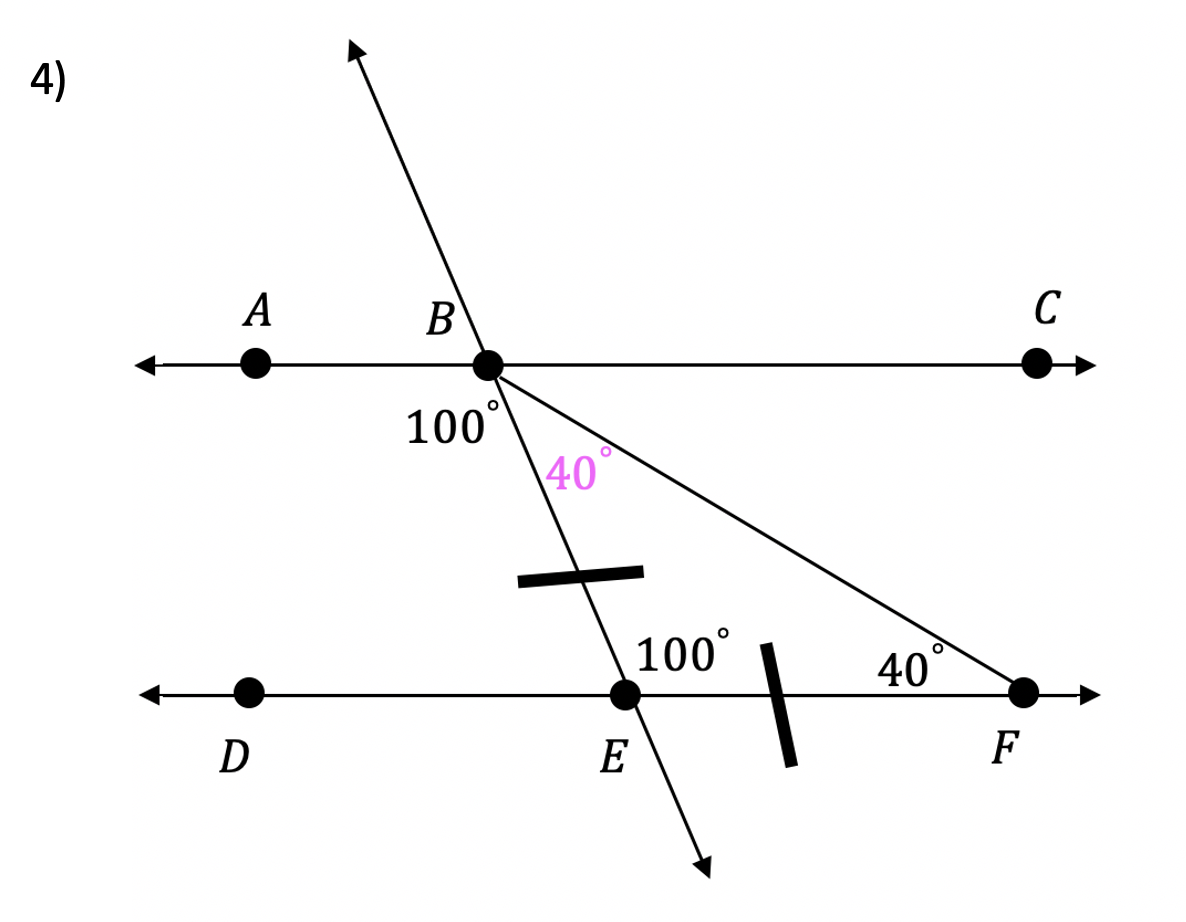
Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Also, if you’re looking to learn about the difference between parallel and perpendicular lines, check out this post here!

Imaginary and Complex Numbers: Algebra 2/Trig.

Happy Wednesday and back to school season math friends! This post introduces imaginary and complex numbers when raised to any power exponent and when multiplied together as a binomial. When it comes to all types of learners, we got you between the video, blog post, and practice problems below. Happy calculating! 🙂

What are Imaginary Numbers?

Imaginary numbers happen when there is a negative under a radical and looks something like this:

Why does this work?

In math, we cannot have a negative under a radical because the number under the square root represents a number times itself, which will always give us a positive number.

Example:

But wait, there’s more:

When raised to a power, imaginary numbers can have the following different values:

Knowing these rules, we can evaluate imaginary numbers, that are raised to any value exponent! Take a look below:

-> We use long division, and divide our exponent value 54, by 4.

-> Now take the value of the remainder, which is 2, and replace our original exponent. Then evaluate the new value of the exponent based on our rules.

What are Complex Numbers?

Complex numbers combine imaginary numbers and real numbers within one expression in a+bi form. For example, (3+2i) is a complex number. Let’s evaluate a binomial multiplying two complex numbers together and see what happens:

-> There are several ways to multiply these complex numbers together. To make it easy, I’m going to show the Box method below:

Try mastering imaginary and complex numbers on your own with the questions below!

Practice:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Don’t forget to sign up for FREE weekly MathSux videos, lessons, and practice questions. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Also, if you’re looking to learn more about dividing polynomials, check out this post here!

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring Review

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Focus and Directrix of a Parabola

Quadratic Equations with 2 Imaginary Solutions

Box and Whisker Plots, IQR and Outliers: Statistics

Ahoy math friends! This post takes a look at one method of analyzing data; box and whisker plots. Box and whisker plots are great for visually identifying outliers and the overall spread of numbers in a data set. We will go over step by step how to create a box and whisker plot given a set of data, we will then look at how to find the interquartile range and upper and lower outliers. If you have any questions, don’t hesitate to check out the video or comment below. Stay curious and happy calculating! 🙂

Looking for more MathSux? Check out this post on variance and standard deviation here!

Box plots look something like this:

Screen Shot 2020-09-02 at 11.19.22 AM.png

Why Box Plots?

Box Plots are a great way to visually see the distribution of a set of data. For example, if we wanted to visualize the wide range of temperatures found in a day in NYC, we would get all of our data (temperatures for the day), and once a box plot was made, we could easily identify the highest and lowest temperatures in relation to its median (median: aka middle number).

From looking at a Box Plot we can also quickly find the Interquartile Range and upper and lower Outliers. Don’t worry, we’ll go over each of these later, but first, let’s construct our Box Plot!

Screen Shot 2020-09-02 at 11.21.28 AM.png

-> First, we want to put all of our temperatures in order from smallest to largest.
-> Now we can find Quartile 1 (Q1), Quartile 2 (Q2) (which is also the median), and Quartile 3 (Q3). We do this by splitting the data into sections and finding the middle value of each section.

Q1=Median of first half of data

Q2=Median of entire data set

Q3=Median of second half of data

-> Now that we have all of our quartiles, we can make our Box Plot! Something we also have to take notice of, is the minimum and maximum values of our data, which are 65 and 92 respectively. Let’s lay out all of our data below and then build our box plot:

Now that we have our Box Plot, we can easily find the Interquartile Range and upper/lower Outliers.

->The Interquartile Range is the difference between Q3 and Q1. Since we know both of these values, this should be easy!

Next, we calculate the upper/lower Outliers.

-> The Upper/Lower Outliers are extreme data points that can skew the data affecting the distribution and our impression of the numbers. To see if there are any outliers in our data we use the following formulas for extreme data points below and above the central data points.

*These numbers tell us if there are any data points below 44.75 or above 114.75, these temperatures would be considered outliers, ultimately skewing our data. For example, if we had a temperature of or these would both be considered outliers.