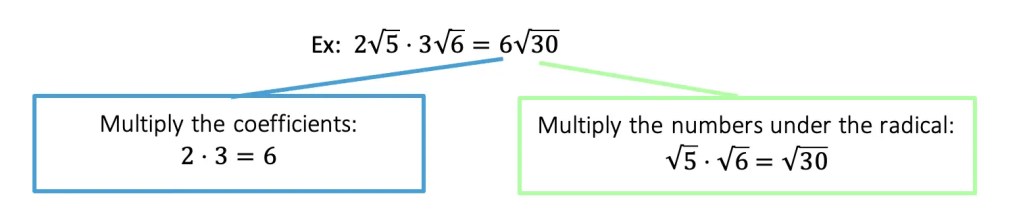
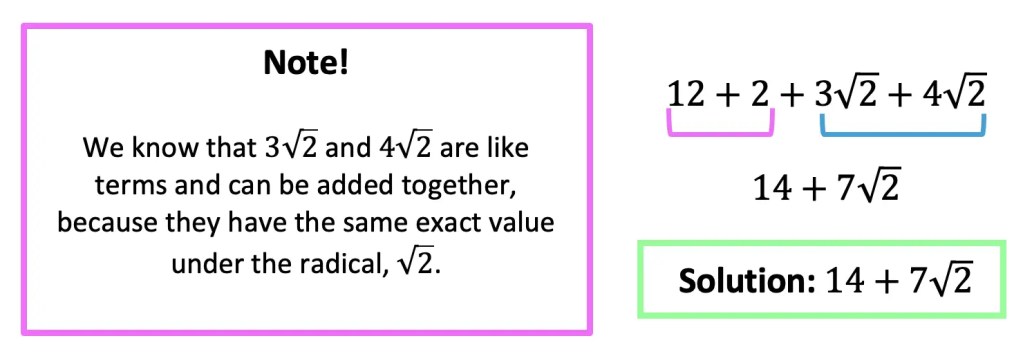
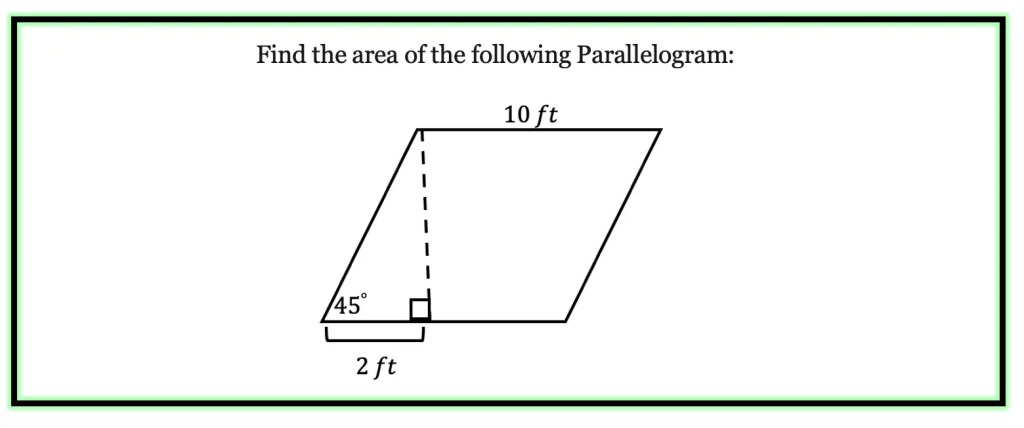
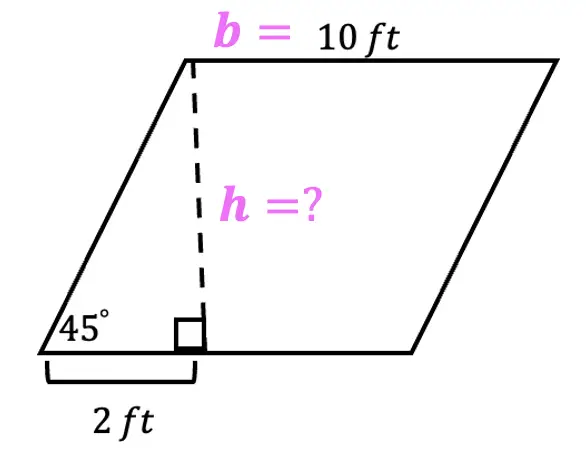
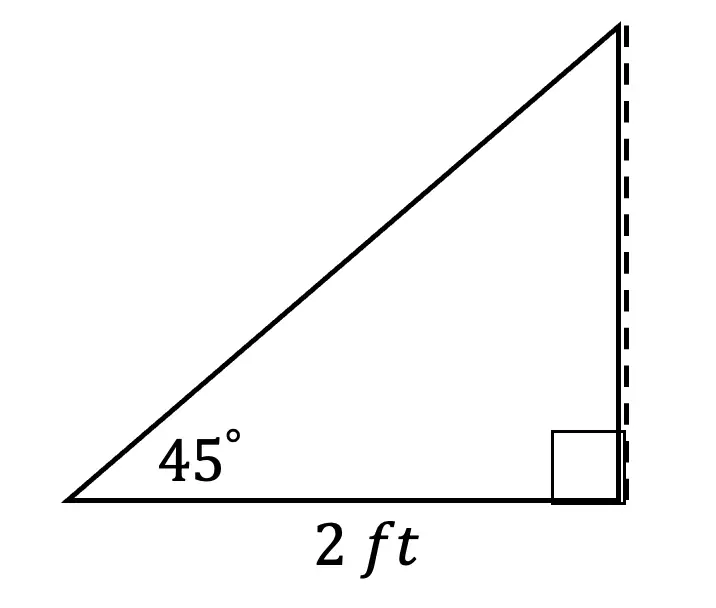
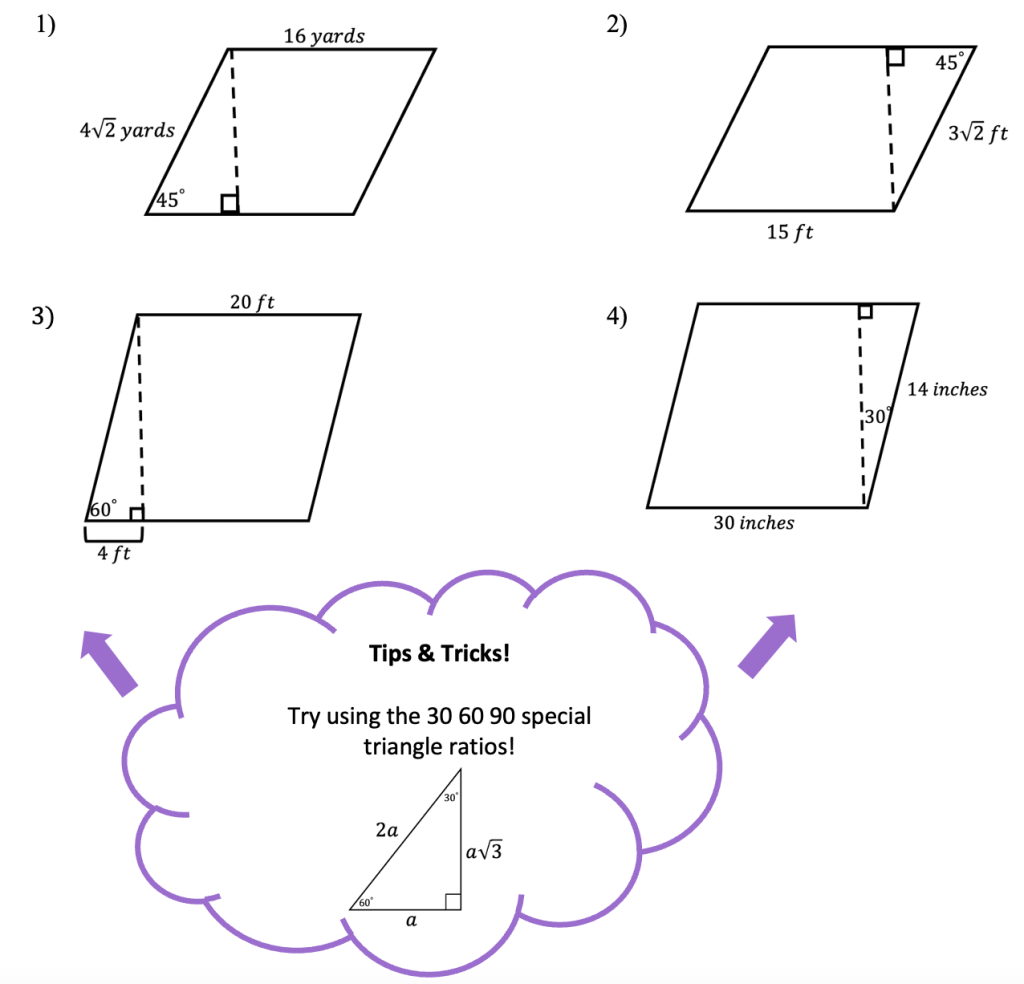
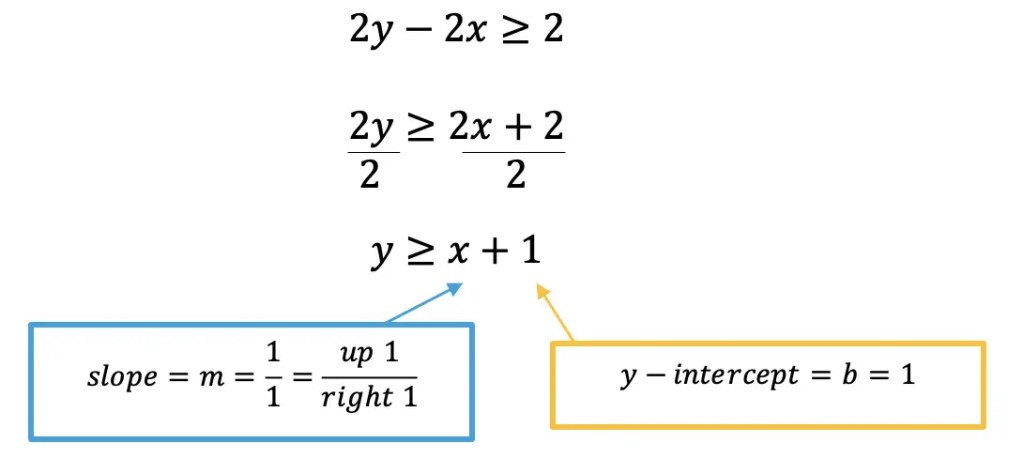
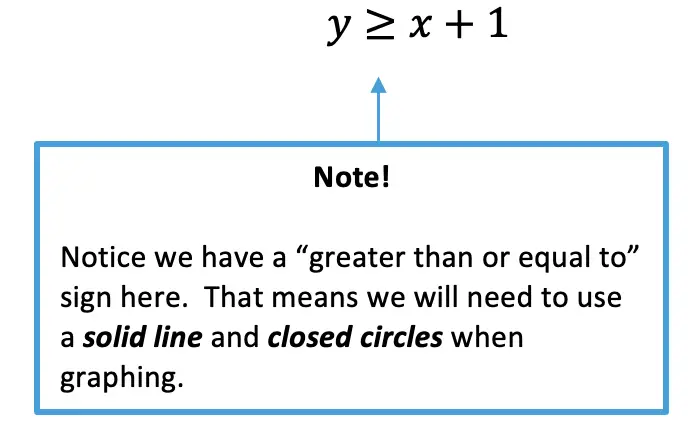
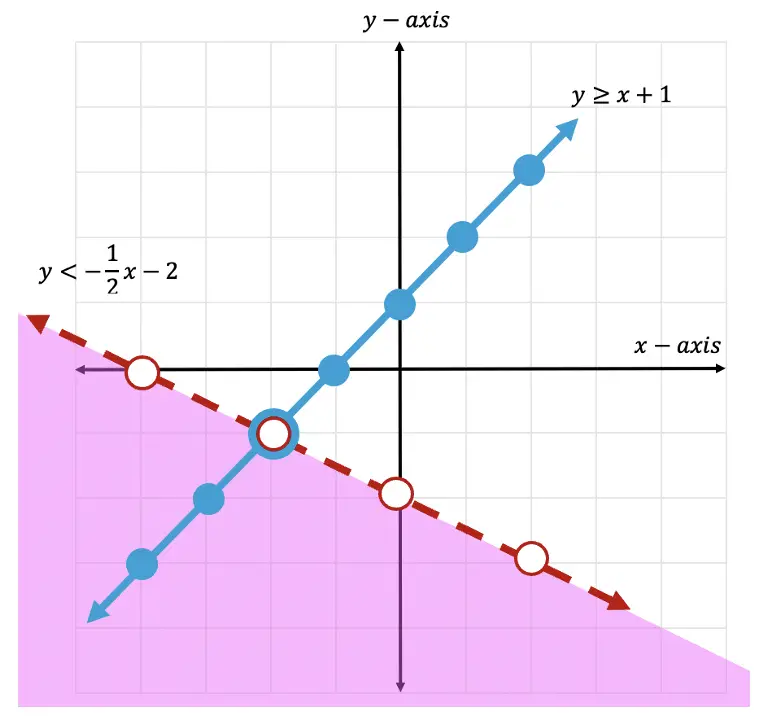
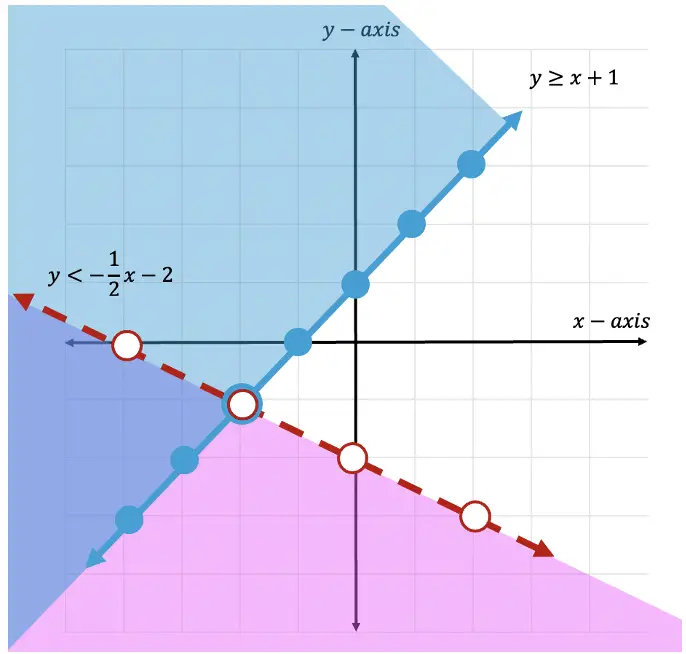
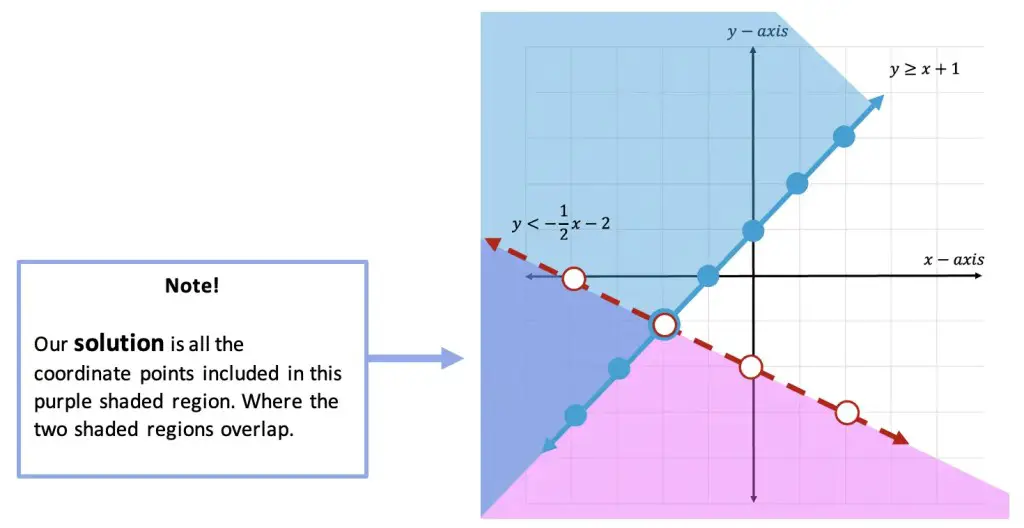
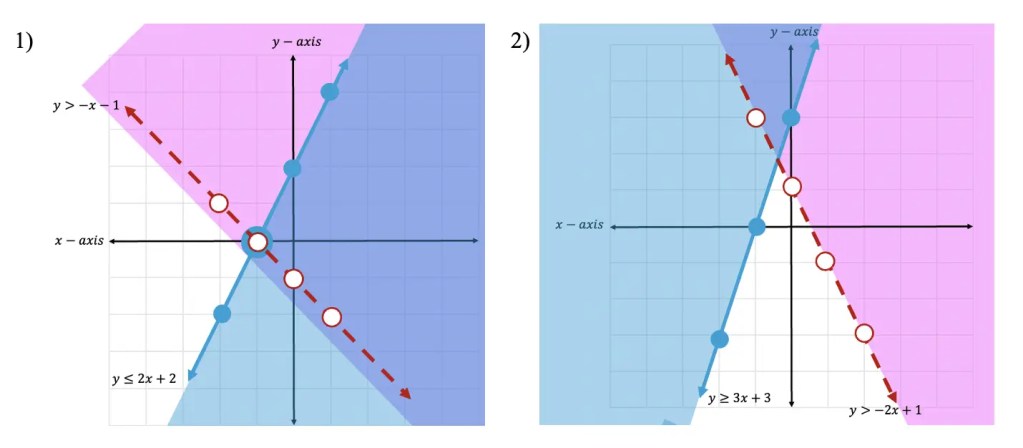
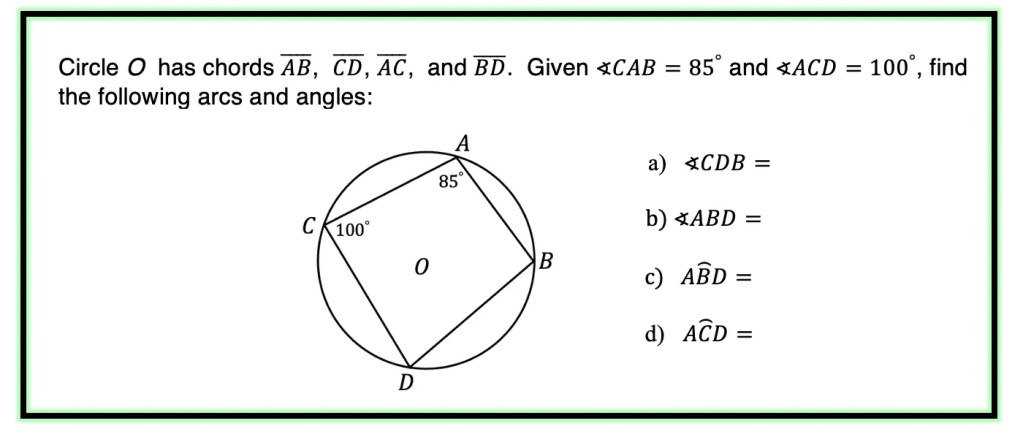
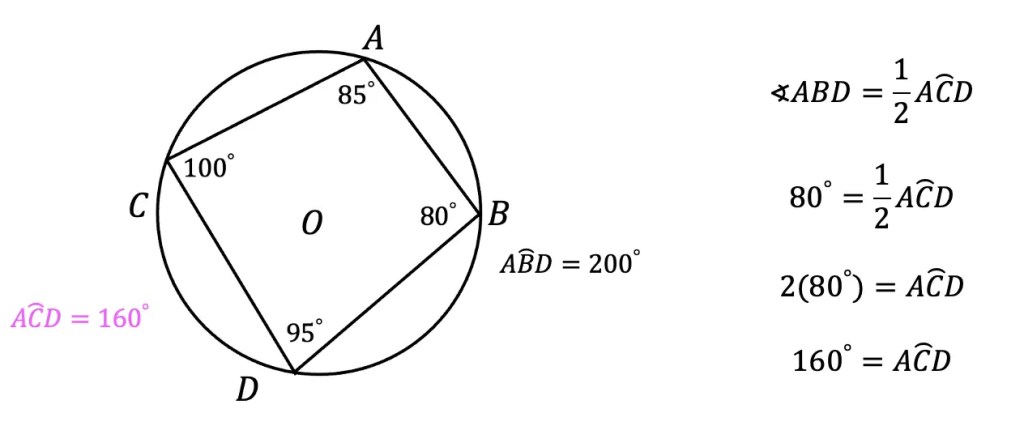
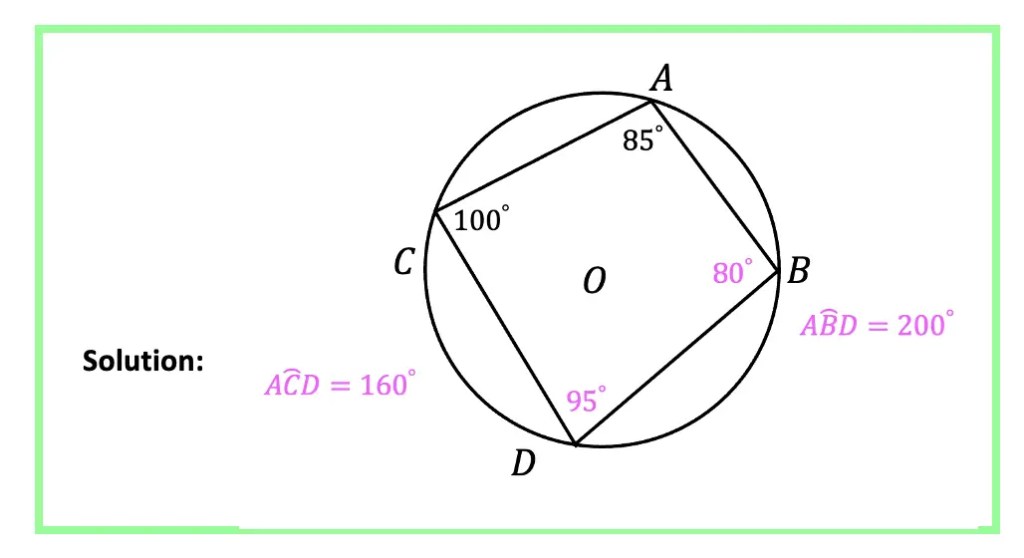
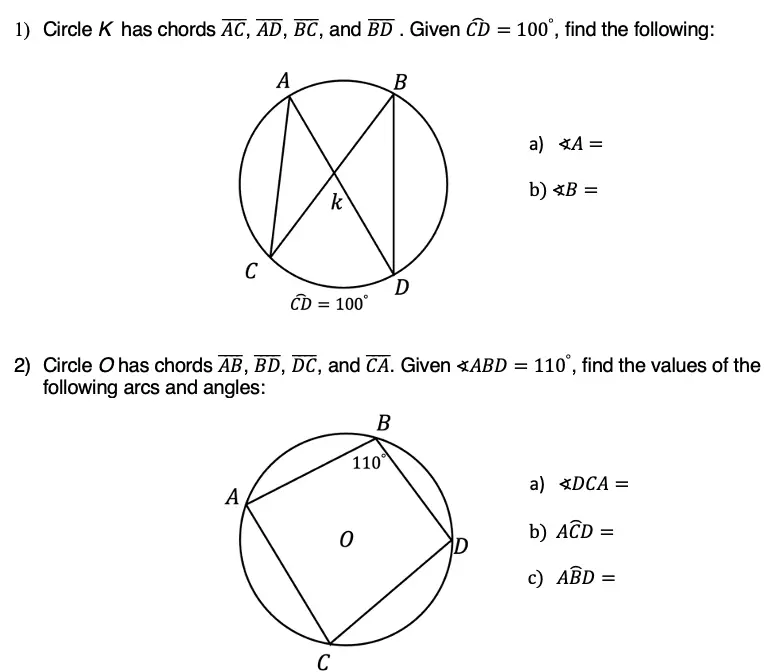
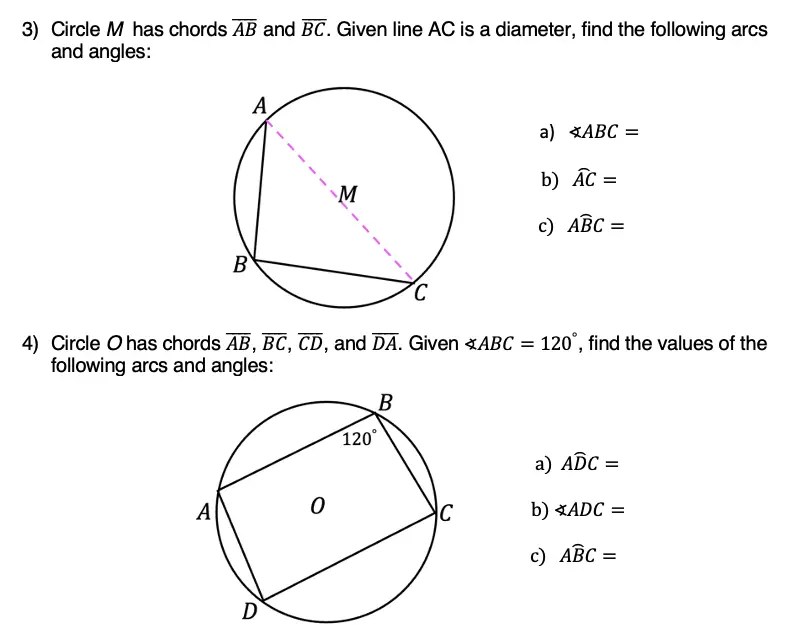
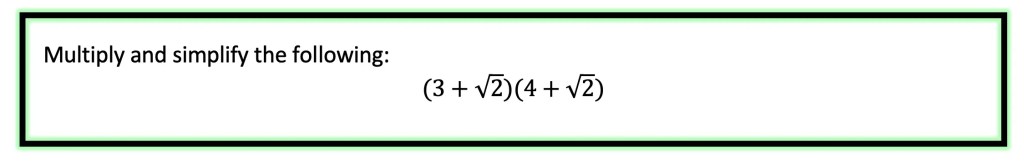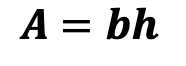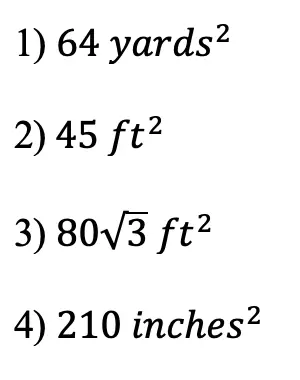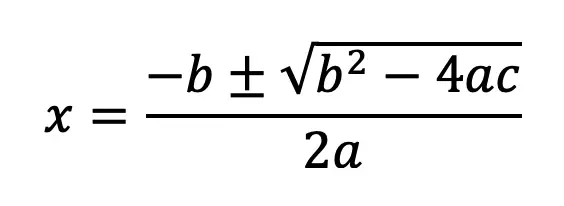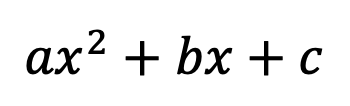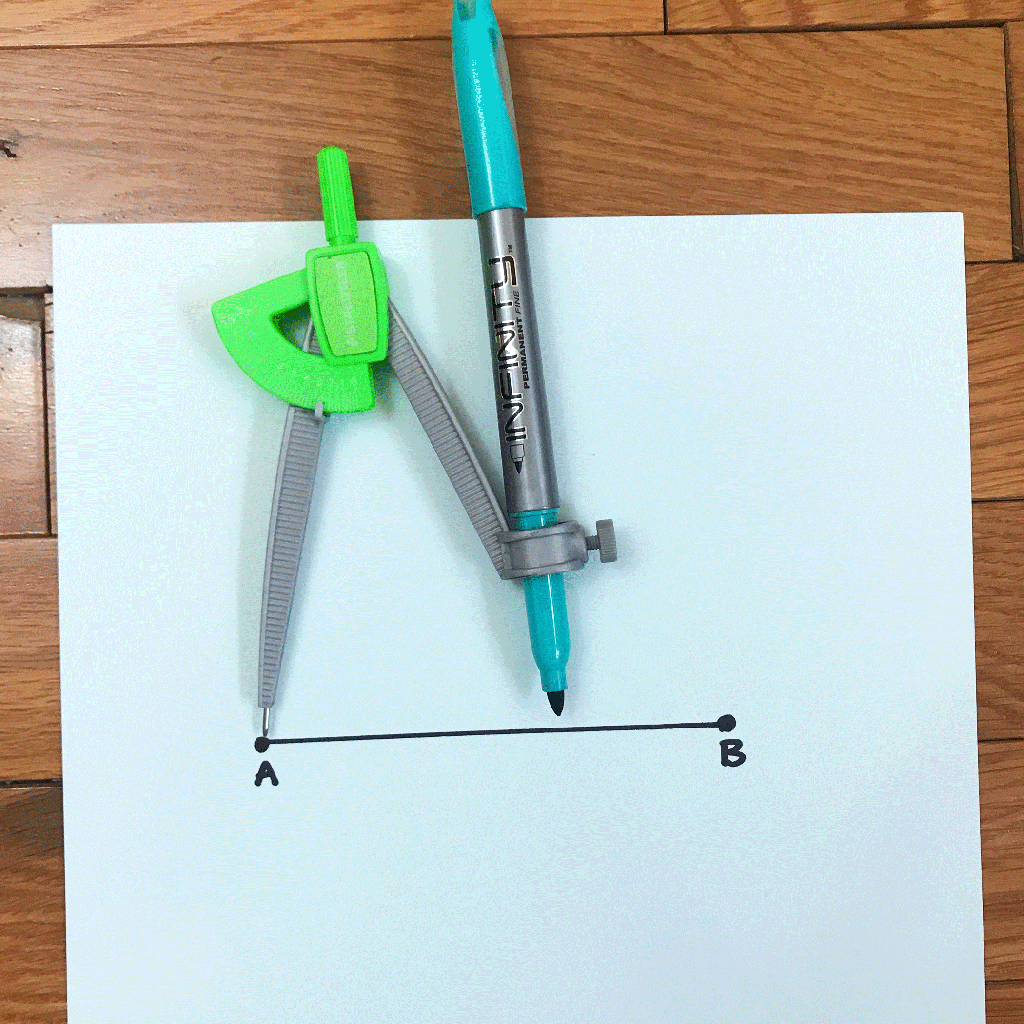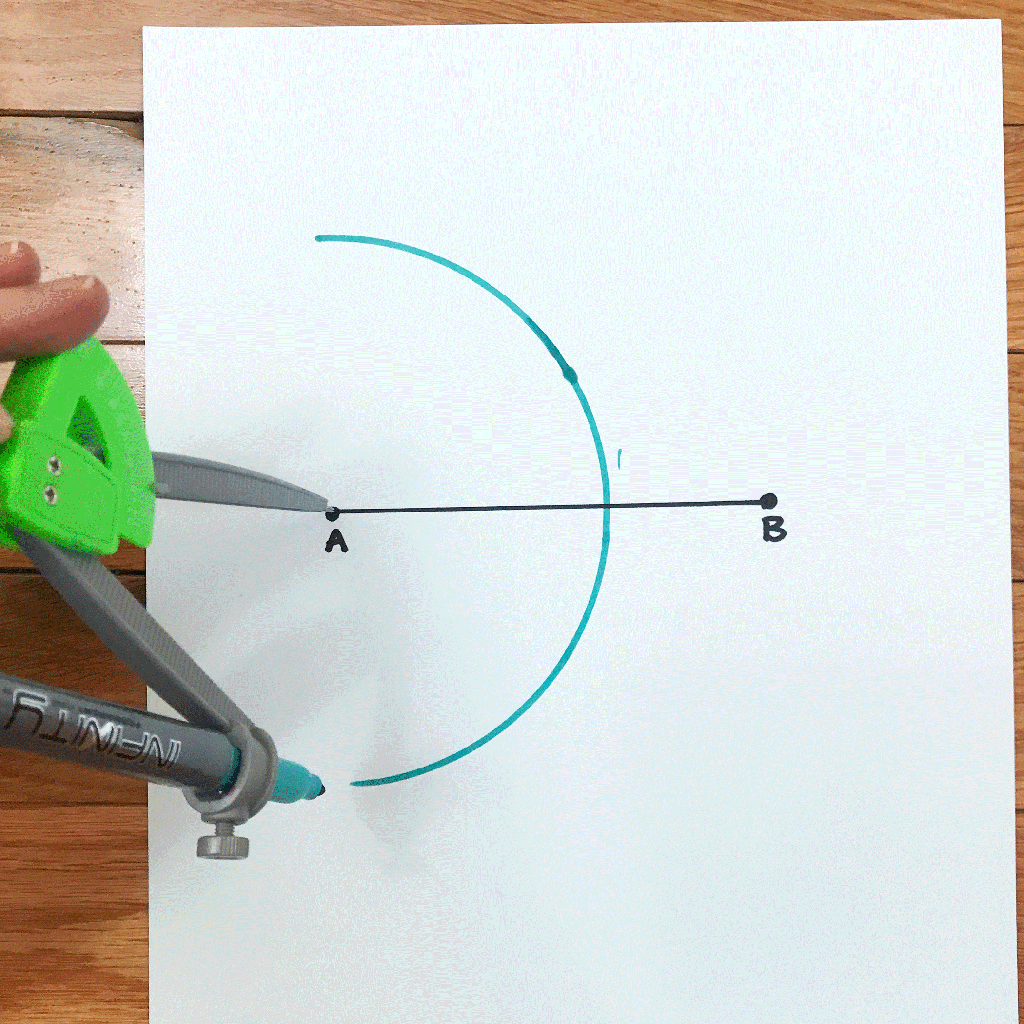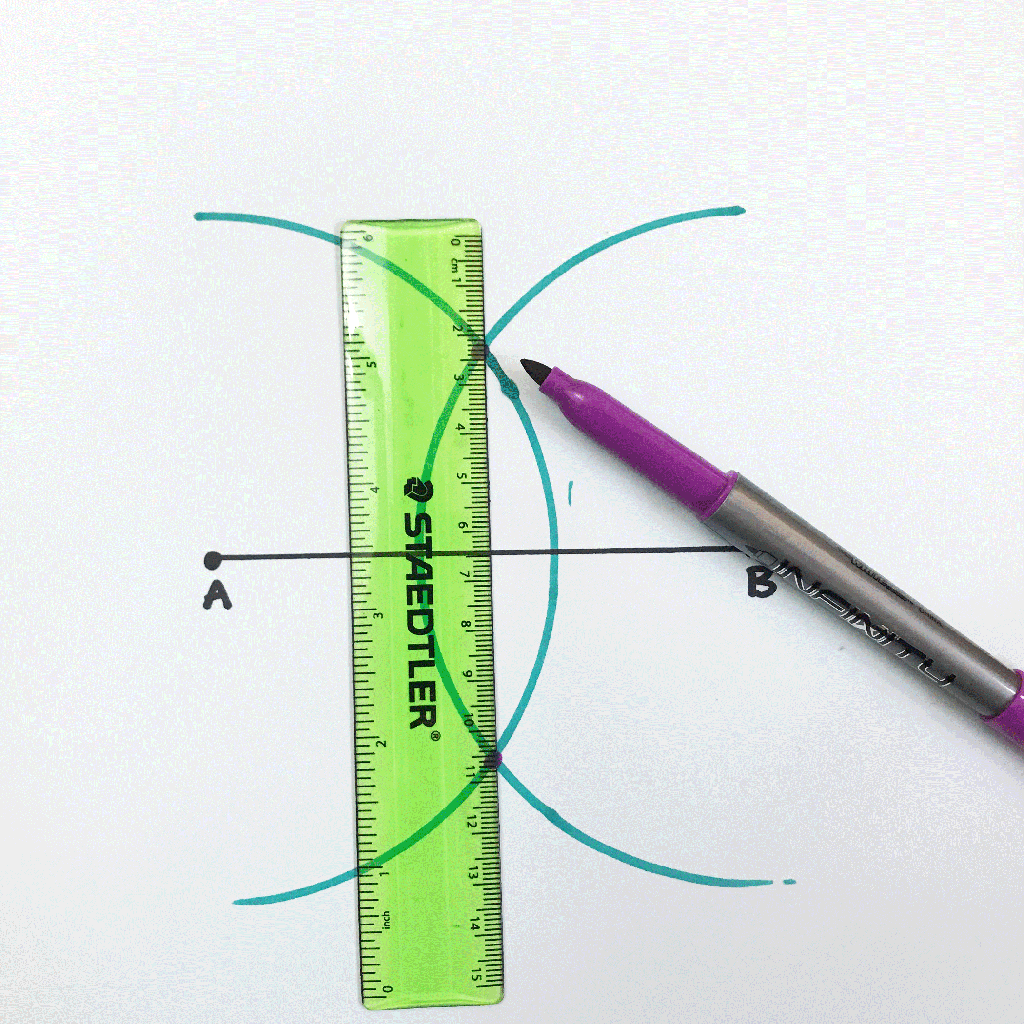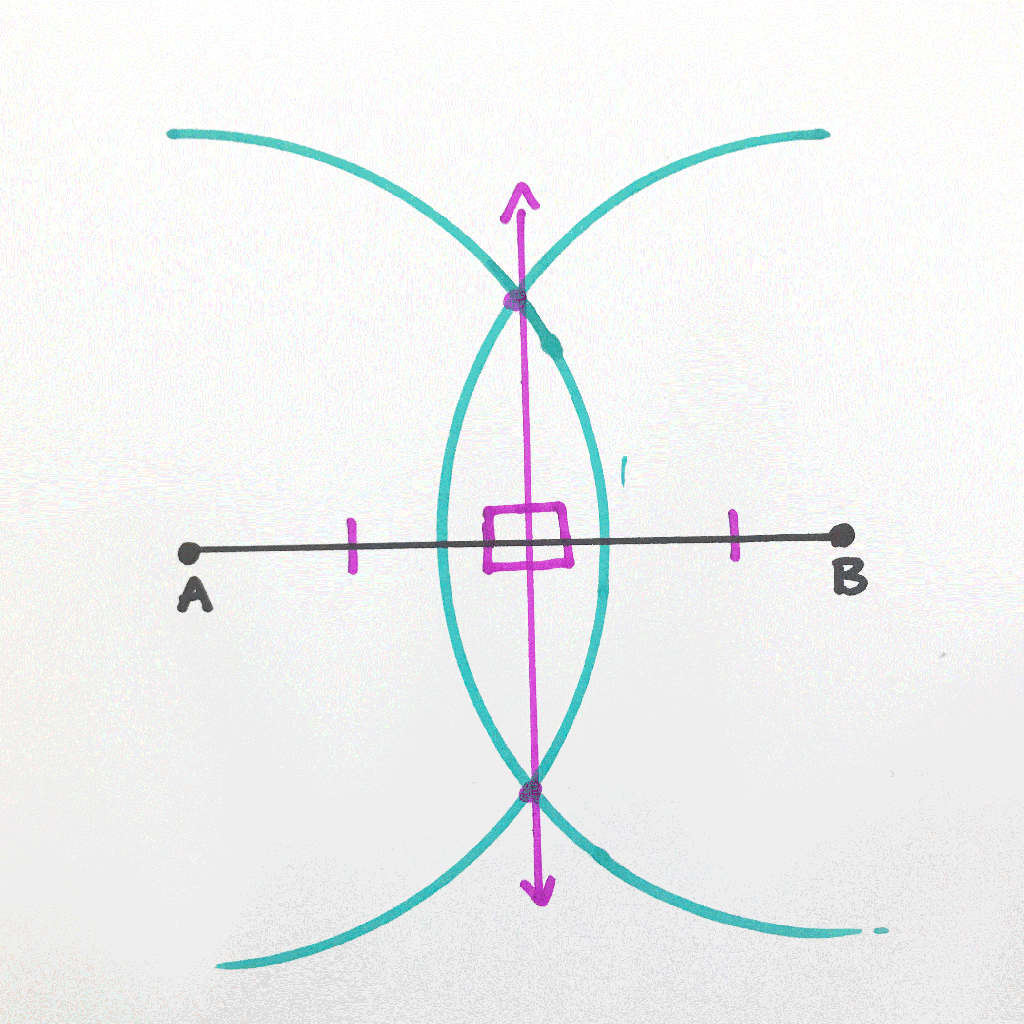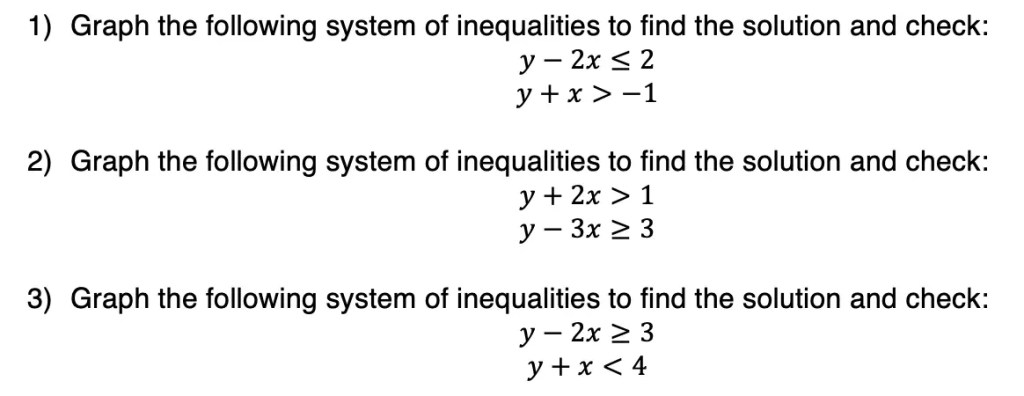Academic Archives - Page 3 of 8

How to Construct a 45 Degree Angle with a Compass

Greeting math friends and welcome to another wonderful week of MathSux! In today’s post we are going to break down how to construct a 45 degree angle with a compass. We will take this step by step starting with a simple straight edge, then we will create a 90 degree angle, and finally we will use an angle bisector to bisect that 90 degree angle to get two 45 degree angles. If you have any questions please don’t hesitate to check out the video and step-by-step GIF below. Thanks so much for stopping by and happy calculating! 🙂

How to Construct a 45 Degree Angle with a Compass:

Step 1: Using a straightedge or a ruler, draw a straight line, labeling each end point A and B.

Step 2: Next, using a compass, place the point of the compass on the edge of point A and draw a circle.

Step 3: Keeping the same length of the compass, take the point of the compass to the point where the circle and line AB intersect. Then swing the compass to make a new arc on the circle above line AB.

Step 4: Keeping that same length of the compass, go to the new intersection we just made and mark another arc along the circle.

Step 5: Now, take a new length of the compass (any will do), and bring it to one of the intersections we made on the circle. Then create a new arc above the circle by swinging the compass.

Step 6: Keep the same length of the compass, bring the compass to the other intersection we made on our circle to create a new arc above the circle.

Step 7: Mark a point where these two lines intersect and using a straight edge, connect this intersection to point A. Notice this forms a 90 degree angle (or a right angle).

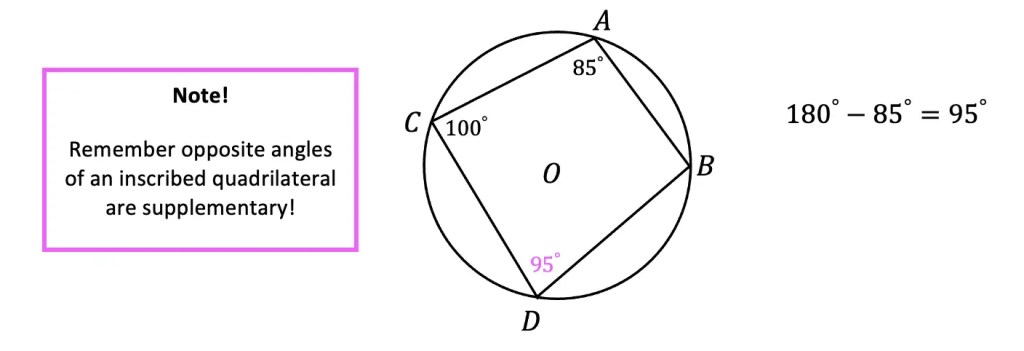
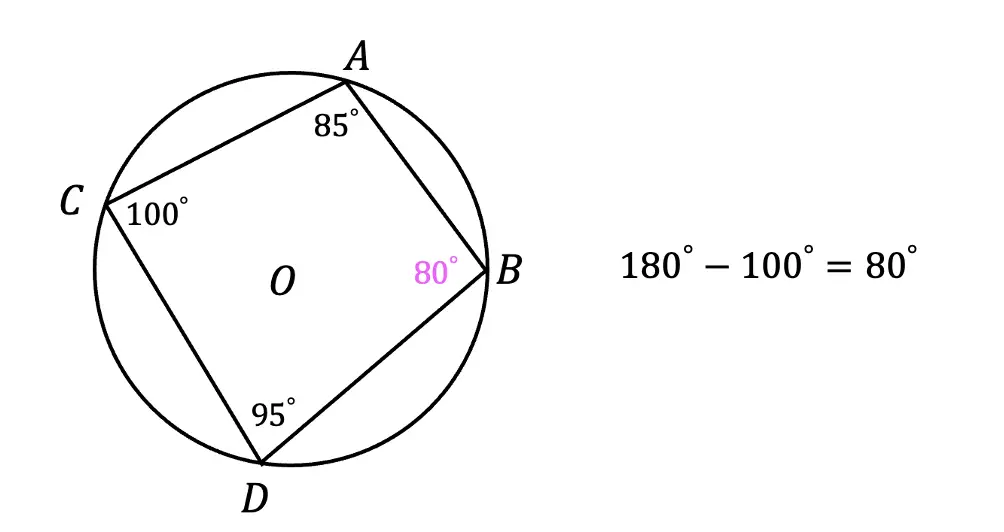
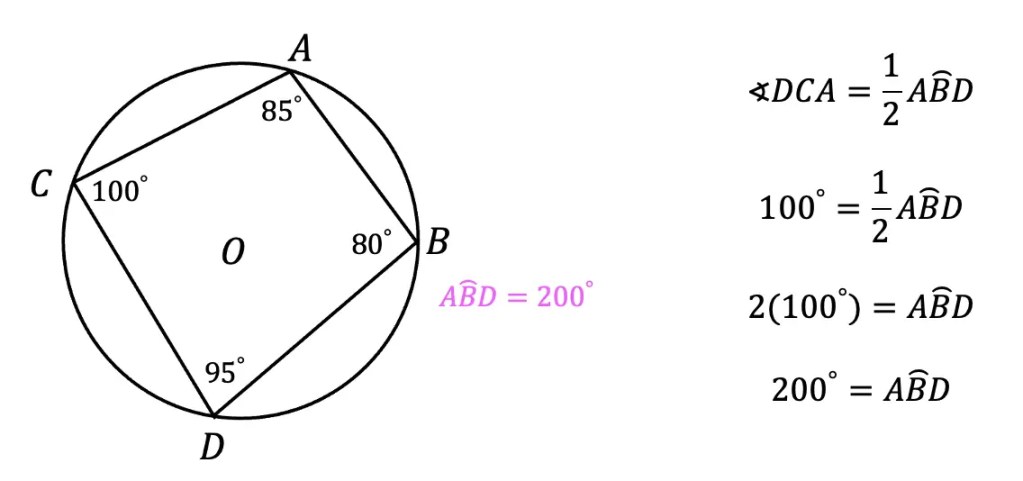
Step 8: Now to bisect our newly made 90 degree angle, we are going to focus on the pink highlighted points where the original circle intersects with line AB and our newly made line.

Step 9: Using a compass (any length), we are going to take the compass point to one of these hi-lighted points and draw another arc.

Step 10: Keeping that same length of the compass, go to the other highlighted point and make another arc as well.

Step 11: Now with a straight edge, draw a line from point A to the new intersection of arcs we just made.

Step 12: Notice we split or 90 degree angle in half and now have two equal 45 degree angles?!

Still got questions? No problem! Don’t hesitate to comment with any questions below or check out the video above. Thanks for stopping by and happy calculating! 🙂

Constructions and Related Posts:

Looking to construct more than just a square inside a circle? Check out these related posts and step-by-step tutorials on geometry constructions below!

Construct an Equilateral Triangle

Perpendicular Line Segment through a Point

Angle Bisector

Construct a Square Inscribed in a Circle

Altitudes of a Triangle (Acute, Obtuse, Right)

How to Construct a Parallel Line

Bisect a Line Segment

Best Geometry Tools!

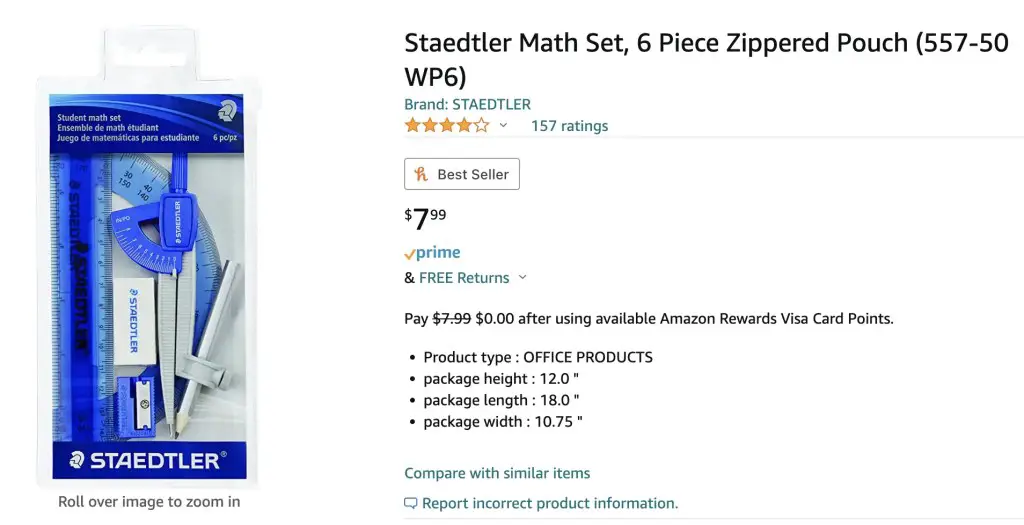
Looking to get the best construction tools? Any compass and straight-edge will do the trick, but personally, I prefer to use my favorite mini math toolbox from Staedler. Stadler has a geometry math set that comes with a mini ruler, compass, protractor, and eraser in a nice travel-sized pack that is perfect for students on the go and for keeping everything organized….did I mention it’s only $7.99 on Amazon?! This is the same set I use for every construction video in this post. Check out the link below and let me know what you think!

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more constructions? Check out how to construct a square inscribed in a circle and an equilateral triangle by clicking on their respective links! And if you’re looking for even more geometry constructions, check out the link here!

Multiplying Radicals Expression

Hi everyone and welcome to MathSux! In today’s post we are going to explore the rules for multiplying radicals, mainly focusing on multiplying binomials expressions that contain radicals. We will go over several types of examples in this post starting with the basics and working our way up to expanding radical binomial expressions and simplifying. If you need a quick review on how to expand binomials using the distributive property/box method, check out this post here. Also, be sure to check out the video and practice questions below. Thanks so much for stopping by and happy calculating! 🙂

What Are the Rules for Multiplying Radicals?

Multiply the coefficients.
Multiply the term or terms under the radical.
Simplify the solution whenever possible.

Check out more completed Examples of multiplying radicals that involve some simplifying below:

The above shows a few simple cases of multiplying radicals but let us take a look at how to multiply radicals that are placed within a binomial within these next Examples.

Step 1: To solve this, we are going to use the distributive property to multiply each term by each term, sometimes known as FOIL (for more on the FOIL method, check out this post, here.)

Step 2: Before we say we are done and have a solution, notice that we can simplify this even more by combining like terms, 12+2=14, we can also combine the like radical terms below because they have the same value of 2 under the radical.

Now, let’s take a look at another type of Example, where we need to first expand binomials that contain radicals.

Step 1: Notice in with this example, we are going to need to expand this binomial and then use the distributive property (or FOIL) to multiply each term by each term.

Step 2: In this case, notice that we can simplify our answer even more by combining like terms.

Try the following practice questions on your own to truly master the topic!

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions below or check out the video above. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Focus and Directrix of a Parabola: Algebra 2

Happy Wednesday math friends! In today’s post are going to go over what the focus and directrix of a parabola are and how to find them. We will also take a look at how to find the equation of a parabola when given the focus and directrix. You may already be familiar with parabolas and quadratic equations, but with this post we will dive deeper into the definition of a parabola and understand it on a whole new level! Don’t forget to check out the video and practice questions, below. Thanks for stopping by and happy calculating! 🙂

Parabola? Vertex? Focus? Directrix? What does it all mean?!

Parabola: A set of all points in a plane that are equidistant from a given point (the focus) and a given line (the directrix). The equation of a parabola in relation to the focus and the directrix is:

Vertex: The maximum or minimum point on a parabola. This coordinate point always lands on the parabola itself. Takes the coordinate form (a,(.5(b+k))) from the parabola equation above.

Focus: A coordinate point that is “inside” the parabola that has the same distance from the vertex as it does the distance between the vertex and directrix. Usually denotes as (a,b) within the parabola equation above.

Directrix: A horizontal line denoted as, “y= ” or “k= “, that is the same distance from the vertex when compared to the distance between the vertex and the focus.

The above definitions explain that every point on a parabola is equidistant from the vertex to the focus as it is to the directrix. In the picture below, we can see that the vertex is 2 units away from the focus and 2 units away from the directrix. They are equidistant:

This phenomenon, works not just the vertex, but for each and every point found on a parabola!

We can see below the equidistance between several points on the parabola that compare the distance between the vertex to the directrix and the distance between the vertex to the focus. Notice that they are all the same!

Ready to test our new knowledge with the following Example?

Step 1: First, let’s sketch out our parabola with the given information. We know that the vertex is at point (2,-1) a point that lies on the parabola itself, so let us map that out. We also know that the directrix is k=3 and is represented as a line as y=-3.

Step 2: Next, let us measure the distance between the directrix and the vertex. The distance between the vertex and directrix is 2 units. That means we must also measure the 2 units on the opposite side of the vertex to find the value of the focus. This leads us to the point (2,1).

Now for part two of our question, how to find the equation of a parabola now that we have the value of the focus and the given directrix. For this, we will need to use the funky looking equation for a parabola mentioned earlier in this post.

Step 1: First we need to gather all of our information, the formula for the equation of a parabola , the given directrix, k=-3 and the focus we found in the previous example (2,1) which corresponds to the formula as a=2 and b=1.

Step 2: Now, let’s plug everything into our formula where a=2, b=1, and k=-3, to find the equation to our parabola:

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Check out similar posts for Algebra 2/Trig. here!

Looking for more on Quadratic Equations and Functions? Check out the following Related posts!

Factoring Review

Factor by Grouping

Completing the Square

4 Ways to Factor a Trinomial

Is it a Function?

Imaginary and Complex Numbers

Quadratic Equations with 2 Imaginary Solutions

What is the Discriminant?

How to find the Area of a Parallelogram: Geometry

Hey math peeps! In today’s post, we are going to go over how to find the area of a parallelogram. There is an easy formula to remember, A=bh, but we are going to look at why this formula works in the first place and then solve a few examples. Just a quick warning: The following examples do use special triangles and if you are need of a review, check out the posts here for 45 45 90 and 30 60 90 special triangles. Also, don’t forget to watch the video and try the practice problems below. Thanks so much for stopping by and happy calculating!

Area of a Parallelogram Formula:

Why does the Formula for Area of a Parallelogram work?

Did you notice that the formula for area of a parallelogram above, base times height, is the same as the area formula for a rectangle? Why?

If we cut off the triangle that naturally forms along the dotted line of our parallelogram, rotated it, and placed it on the other side of our parallelogram, it would naturally fit like a puzzle piece and create a rectangle! Check it out below:

Now that we know where this formula comes from, let’s see it in action in the examples below:

Example #1:

Step 1: Write out the formula:

Step 2: Fill in the formula with values found on our parallelogram, b=12 inches h=4 inches, and multiply them together to get 48 inches squared.

That was a simple example, but lets try a harder one that involves special triangles.

Example #2:

Step 1: Write out the formula:

Step 2: Label the values found on our parallelogram, b=10 ft and notice that we are going to need to find the value of the height.

Step 3: In order to find the value of the height, we need to remember our special triangles! We are not given the value of the height, but we are given some value of the triangle that is formed by the dotted line. Let us take a closer look and expand this triangle:

Step 4: We can add in the missing 45º degree value so that our triangle now sums to 180º.

Step 5: Remember 45 45 90 special triangles? (If you need a review click the link). Because that is exactly what we are going to need to find the value of the height! Below is our triangle on the left, and on the right is the 45 45 90 triangle ratios we need to know to find the value of the height.

Based on the above ratios, we can figure out that the height value is the same value as the base of the triangle, 2.

Step 6: If we place our triangle back into the original parallelogram, we can plug in our value for the height, h=2, into our formula to find the area:

When you’re ready, check out the practice questions below!

Practice Questions:

Find the area of each parallelogram:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Quadratic Equations with Two Imaginary Solutions

Hi everyone and welcome to MathSux! In today’s post we are going to be solving quadratic equations by using the quadratic formula. You may have used the quadratic formula before, but this time we are working with quadratic equations with two imaginary solutions. All this means is that there are negative numbers under the radical that have to be converted into imaginary numbers. If you need a review on imaginary numbers or the quadratic formula before reading this post, check out these links! Thanks so much for stopping by and happy calculating! 🙂

What is the Quadratic Formula?

The Quadratic formula is a formula we use to find the x-values of a quadratic equation. When we find the x-value of a quadratic equation, we are actually finding its x-values on the coordinate plane. Check out the formula below:

where, a, b, and c are coefficients based on the quadratic equation in standard form:

What does it mean to have “Imaginary Roots”?

When we solve for the x-values of a quadratic equation, we are always looking for where the equation “hits” the x-axis. But when we have imaginary numbers as roots, the quadratic equation in question, never actually hit the x-axis. Ever. This creates a sort of “floating” quadratic equation with complex numbers as roots. See what it can look like below:

Ready for an Example? Let us see how to use the quadratic formula specifically, quadratic equations with two imaginary solutions:

Think you are ready to try practice questions on your own? Check out the ones below!

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions below or check out the video above. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Factor By Grouping Examples: Algebra

Hey there math peeps and welcome to MathSux! In today’s post we are going to cover factor by grouping examples, a surprisingly cool and easy factoring method used to factor quadratic equations when “a” is greater than one. It can also be used to factor four term polynomials. We are going to look at an example of each below. If you have any questions, please don’t hesitate to check out the video and try the practice problems at the end of this post. Thanks for stopping by and happy calculating! 🙂

What is Factor by Grouping?

Factor by Grouping is a factoring method that groups common factors of an algebraic expression together. Many times, we use factoring to find the x-values of a quadratic equation when the coefficient “a” is greater than 1.

When should we use Factor by Grouping?

1) If the first coefficient in a quadratic equation, a, is greater than 1:

2) When there is a polynomial with 4 terms:

Factor by Grouping Examples:

Ready for an Example? Let us look at how to factor a quadratic equation when a is greater than one.

Now, let’s take a look at another type of example, that can be solved with the help of factor by grouping!

Notice that this question is actually easier to solve than the last! The polynomial above, is already split into 4 terms, therefore, we can jump ahead, skipping the product/sum steps we did in the previous example!

Ready to try practice questions on your own? Check them out below to master Factor by Grouping!

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking to learn about different Factoring methods and functions? Check out the related posts below!

GCF, Product/Sum, Difference of Two Squares, Quadratic Formula

Quadratic Formula, Product/Sum, Completing the Square, Graph

Completing the Square

The Discriminant

Is it a Function?

Quadratic Equations with 2 Imaginary Solutions

Free High School Math Resources

Greetings math friends! Today’s post is for the New York state teachers out there in need of a lesson boost. In this post, we’ll go over what MathSux has to offer for free high school math resources including videos, lessons, practice questions, etc. Remember everything you see here is 100% free and designed to make your life (and your students’ life) easier.

Signing up with MathSux will get you access to FREE:

1) Math Videos

2) Math Lessons

3) Practice Questions

4) NYS Regents Review

Everything designed here aligns with the NYS Common Core Standards for Algebra, Geometry, Algebra 2/Trig. and Statistics.

I am a NYS math teacher that creates free math videos, lessons, and practice questions every week, right here, for you! On the YouTube channel, you’ll also find NYS Common Core Regents questions reviewed one question at a time.

Featured on Google Classrooms around the world, MathSux.org is a great resource especially now, in the time of COVID and zooming and schooling from home. I hope you stick around and find these resources helpful.

And if you’re looking to get the latest MathSux.org videos and emails straight to your inbox, don’t forget to sign up on the right hand-side of the website. Thanks so much for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Bisect a Line Segment

Hi everyone and welcome to MathSux! In this post we are going to be constructing a perpendicular bisector by using a compass and stright edge. A perpendicular bisector, (also known as a segment bisector), is a line that cuts a line segment in half and creates four 90º angles. It is a super fast and super simple construction! We’ll also go over the Perpendicular Bisector Theorem we can infer from our original construction. If you’re looking for more geometric constructions, don’t forget to check more out here. Thanks so much for stopping by and happy calculating! 🙂

What is the Perpendicular Bisector of a line segment?

A perpendicular bisector slices our line segment AB (or any line segment) in half at its midpoint, creating two equal halves.
This will also create a 90º angle ( or right angle) about the line.

Constructing a Perpendicular Bisector through line segment AB

What is happening in this GIF?

Step 1: Notice we are given line segment AB. First, we are going to measure out a little more than halfway across the line segment AB by using a compass.

Step 2: Next we are going to place the point of the compass on point A and swing above and below line segment AB to create a half circle.

Step 3: Keeping the same distance on our compass, we are then going to place the point of the compass onto Point B (the opposite side) and repeat the same step we did on point A, drawing an arc in the shape of a semi-circle.

Step 4: Notice the intersection point above and below line segment AB!? Now, we are going to connect these two points by drawing a line with a ruler or straightedge.

Step 5: Yay! We now have a segment bisector! This cuts line segment AB right at its midpoint, while also dividing line segment AB into two equal halves and creating a 90º angle around our two intersecting lines.

Perpendicular Bisector Theorem:

The Perpendicular Bisector Theorem explains that any point along the perpendicular bisector line we just create is equidistant to each end point of the original line segment (in this case line segment AB).

Therefore, if we were to draw points C,D, and E along the perpendicular bisector, then draw imaginary lines stemming from these points to each end point, we’d get something like the image below:

AC = CB

AD = DB

AE = EB

Notice that with each of our points on the perpendicular line above, we can now state that the following is true:

AC = CB

AD = DB

AE = EB

The fact that we can state the above is true is reason for the Perpendicular Bisector Theorem!

Constructions and Related Posts:

Looking to construct more than just a perpendicular segment bisector? Check out these related posts and step by step tutorials on geometry constructions below!

Construct an Equilateral Triangle

Perpendicular Line through a Point

Angle Bisector

Construct a 45º angle

Altitudes of a Triangle (Acute, Obtuse, Right)

Construct a Square inscribed in a Circle

Best Geometry Tools!

Looking to get the best construction tools? Any compass and straight edge will do the trick, but personally, I prefer to use my favorite mini math toolbox from Staedler. Stadler has a geometry math set that comes with a mini ruler, compass, protractor, and eraser in a nice travel-sized pack that is perfect for students on the go and for keeping everything organized….did I mention it’s only $7.99 on Amazon?! This is the same set I use for every construction video! Check out the link below and let me know what you think!

Still got questions? No problem! Don’t hesitate to comment with any questions below or check out the video above. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Want to see how to construct a square inscribed in a circle? Or maybe you want to construct an equilateral triangle? Click on each link to view each construction! And if you’re looking for even more geometry constructions, check out the link here! And if you’re looking for a construction you don’t yet see, please be sure to suggest it in the comments below!

How to Solve Inequalities with 2 Variables: Algebra

Hi everyone and happy Wednesday! Today we are going to look at how to solve inequalities with 2 variables. You may hear this in your class as “Simultaneous Inequalities” or “Systems of Inequalities,” all of these mean the same exact thing! The key to answering these types of questions, is to know how to graph inequalities and to know that the solution is always found where the two shaded regions overlap each other on the graph. We’re going to go over an example one step at time, then there will be practice questions at the end of this post that you can try on your own. Happy calculating! 🙂

How to Solve Inequalities with 2 Variables:

Just to review, when graphing linear inequalities, remember, we always want to treat the inequality as an equation of a line in form….with a few exceptions:

1)Depending on what type of inequality sign we are graphing, we will use either a dotted line and an open circle (< and >) or a solid line and a closed circle (> or <) and to correctly represent the solution.

2) Shading is another important feature of graphing inequalities. Depending on the inequality sign we will need to either shade above the x-axis ( > or > ) or below the x-axis ( < or < ) to correctly represent the solution.

3) Solution: To find the solution of a system of inequalities, we are always going to look for where the shaded regions of both inequalities overlap.

How to Solve Inequalities with 2 Variables

Now that we know the rules, of graphing simultaneous inequalities, let’s take a look at an Example!

Step 1: First, let’s take our first inequality, and get it into y=mx+b form. To do this, we need to move .5x to the other side of the inequality by subtracting it from both sides. Once we do that, we can identify the slope and the y-intercept.

Step 2: Before graphing, let’s now identify what type of inequality we have here. Since we are working with a < sign, we will need to use a dotted line and open circles when graphing.

Step 3: Now that we have identified all the information we need to, let’s graph the first inequality below:

Step 4: Now it is time for us to shade our graph, since this is an inequality, we need to show all of our potential solutions with shading. Since we have a less than sign, <, we will be shading below the x-axis. Notice all the negative y-values below are included to the left of our line. This is where we will shade.

Step 5: Next, let’s start graphing our second inequality! We do this by taking the second equation, and getting it into y=mx+b form. To do this, we need to move 2x to the other side of the inequality by adding it to both sides. Then we can simplify the inequality even further by dividing out a 2.

Step 6: Before graphing, let’s now identify what type of inequality we have here. Since we are working with a > sign, we will need to use a solid line and closed circles when creating our graph.

Step 7: Now that we have identified all the information we need to, let’s graph the second inequality below:

Step 8: Now it is time for us to shade our graph. Since we have a greater than or equal to sign, >, we will be shading above the x-axis. Notice all the positive y-values above are included to the left of our line. This is where we will shade.

Where is the solution?!

Step 9: The solution is found where the two shaded regions overlap. In this case, we can see that the two shaded regions overlap in the purple section of this graph.

Step 10: Check! Now we can finally check our work. To do that, we can choose any point within our overlapping purple shaded region, if the coordinate point we choose holds true when plugged into both of our inequalities then our graph is correct!

Let’s take the point (-4,-1) and plug it into both original inequalities where x=-4 and y=-1.

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking to review graphing linear inequalities Check out this post on here!

Inscribed Angles & Intercepted Arcs: Geometry

Ahoy math friends and welcome to MathSux! In this post, we are going to go over the inscribed angle theorem which dives into inscribed angles and intercepted arcs. We’ll break down the main basic rule for inscribed angle theorem and the three inscribed angle theorems associated with this rule. If you are looking for more circle theorems, check out these posts on the Intersecting Secants Theorem and Central Angles Theorem. Also, don’t forget to check out the video and practice questions to truly master the topic below. Happy calculating! 🙂

Inscribed Angles:

When two chords come together to touch the outline of a circle, they create something called an inscribed angle. Unlike central angles, an inscribed angle is equal to half the measure of the arc length. In the example below, we can see that the inscribed angle ACB is equal to 25º while its corresponding intercepted arc AB is twice the inscribed angle at 50º. Knowing this allows us to find the value of unknown arcs or inscribed angles.

Inscribed Angle Theorem:

There are three parts to the inscribed angle theorem to know based on the rule stated above, check them out below!

The inscribed angle theorem states that, in a circle when two inscribed angles intercept the same arc, the angles are congruent. Notice below how angle A and angle B both have the same arc CD (hi-lighted in pink). In this theorem, we have two inscribed angles, angle A and angle B, that intercept the same arc, arc CD.

Theorem #2: In a circle when an angle is inscribed by a semicircle, it forms a 90º angle (or a right angle). If you look at angle BAC below, you’ll notice that the arc it corresponds with is a semicircle and that angle BAC forms a right angle.

Theorem #3: When a quadrilateral is inscribed within a circle, the opposite angles formed are supplementary, meaning that they add to 180º. The proof below shows angles A and C (hi-lighted in green) as supplementary, but this proof would also work for opposite angles B and D (hi-lighted in pink).

Let’s look at how to apply these rules with an Example:

a) Step 1: To find the value of angle CDB we need to look at our given information. We know that angle CAB=85º, notice that this follows theorem number 3, “When a quadrilateral is inscribed in a circle, opposite angles are supplementary.” Therefore, we must subtract 110º from 180º to find the value of angle CDB.

b) Step 2: For finding angle ABD, we’re going to use the same theorem we used in part a, opposite supplementary angles of an inscribed quadrilateral are supplementary.

c) Step 3: Next, to find the value of arc ABD, we need to use the basic inscribed angle theorem that tells us an inscribed angle is equal to half the measure of its arc. Then use some basic algebra to solve for arc ABD.

d) Step 4: To find arc ACD, we need to use the basic inscribed angle theorem that tells us an inscribed angle is equal to the value of its arc, then use algebra to solve similar to part c.

If this looks confusing, check out the video above! And when you are ready master this topic with the practice questions below!

Practice Questions:

Use the inscribed angle theorem outlined above to answer the following questions.

Solutions:

Still got questions? No problem! Check out the video above or comment below for any questions and follow for the latest MathSux posts. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more posts on Circle Theorems? Check out the posts below!