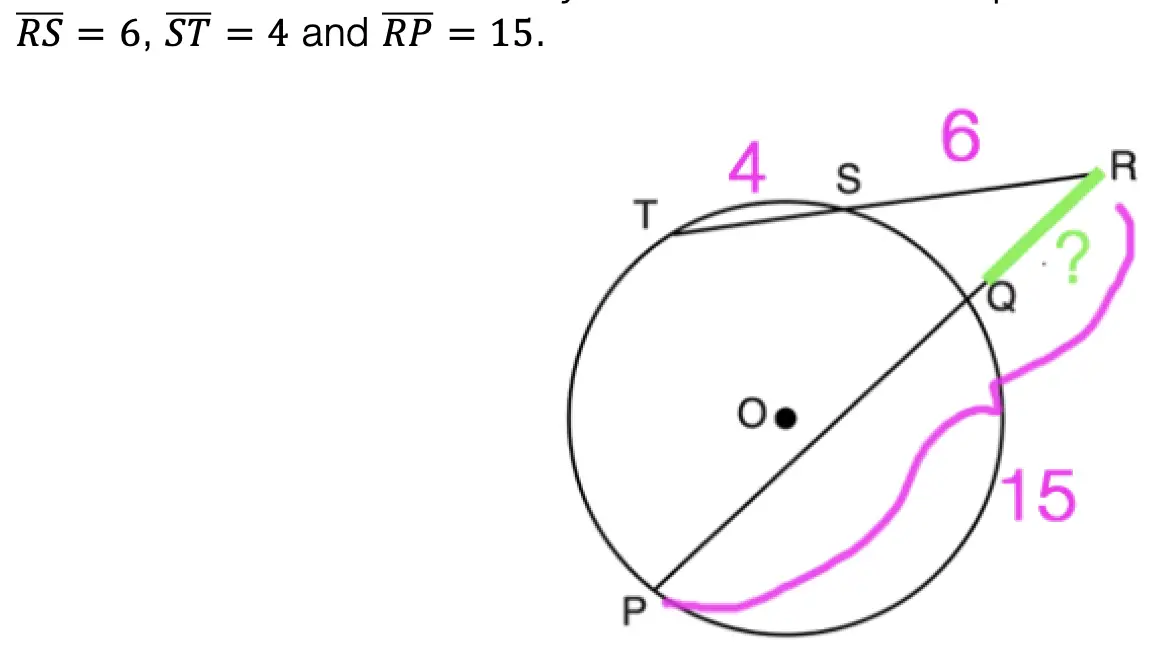
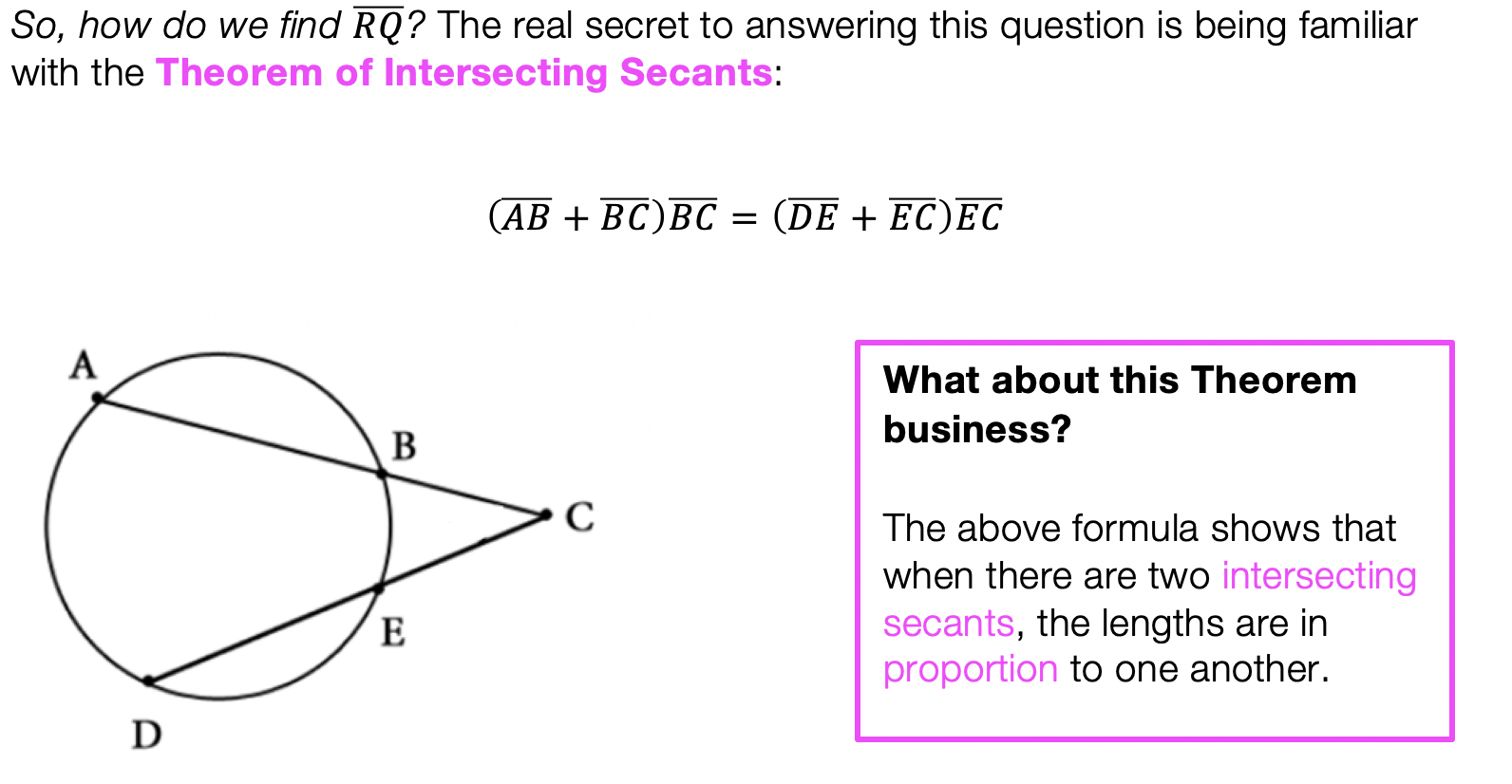
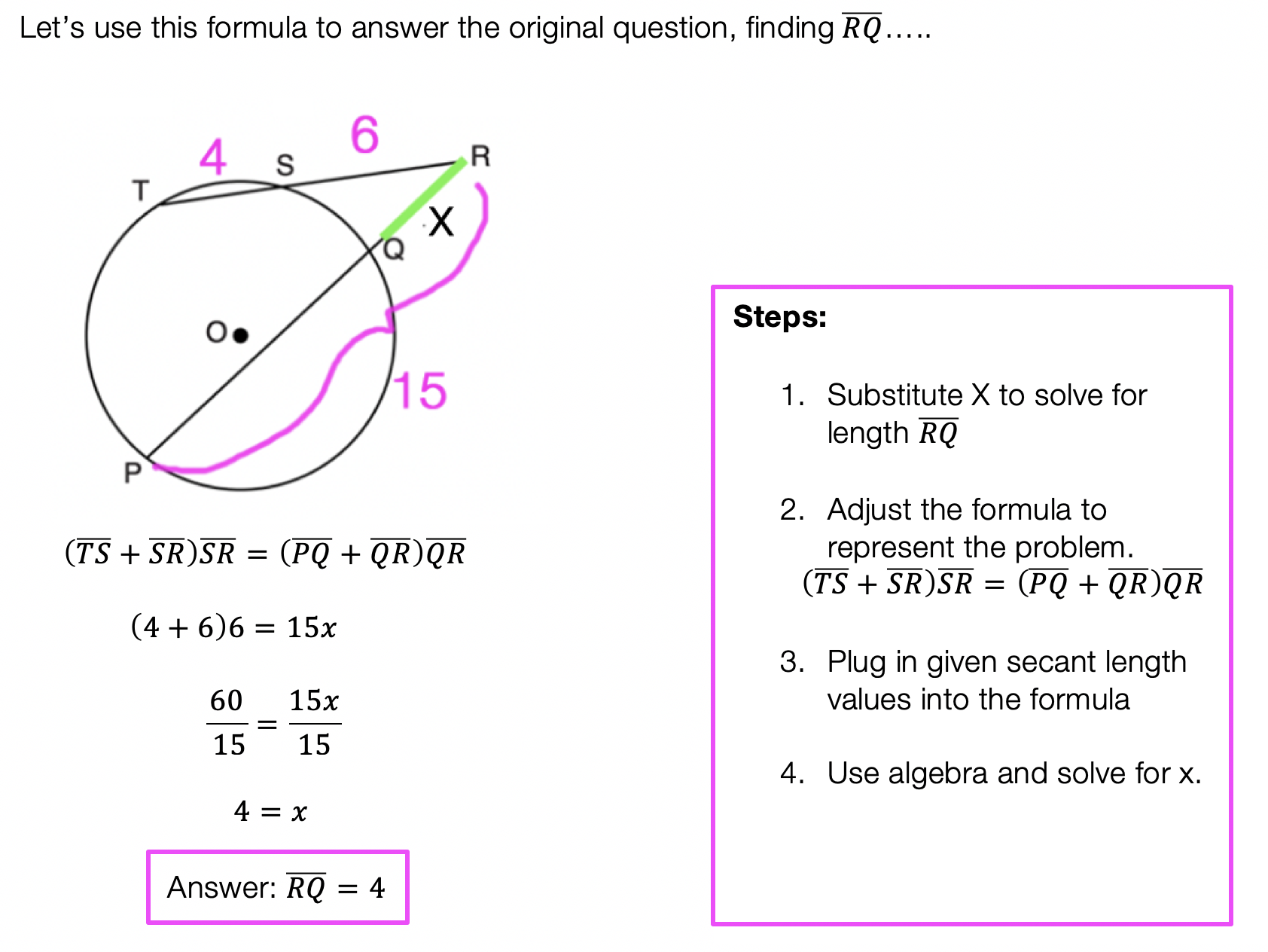
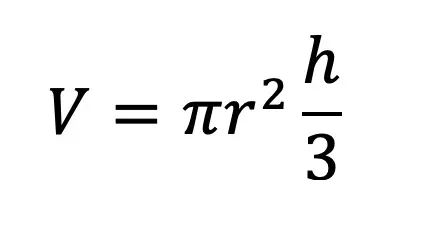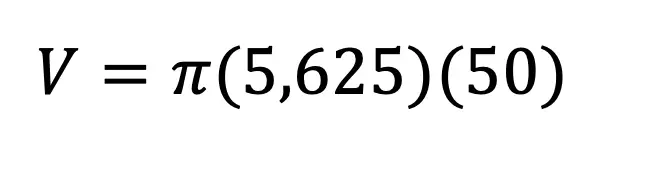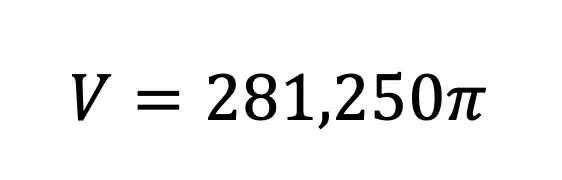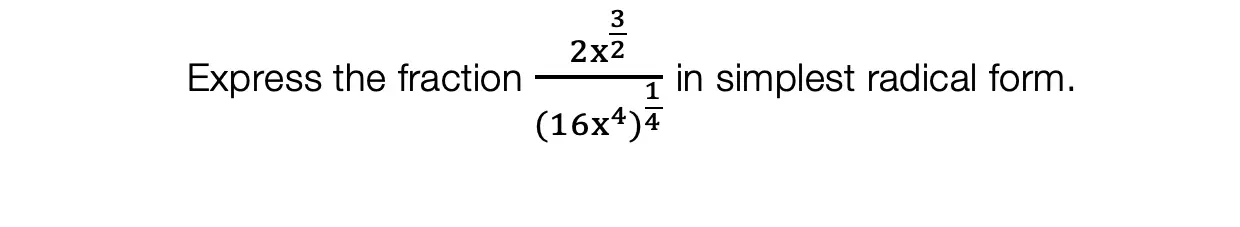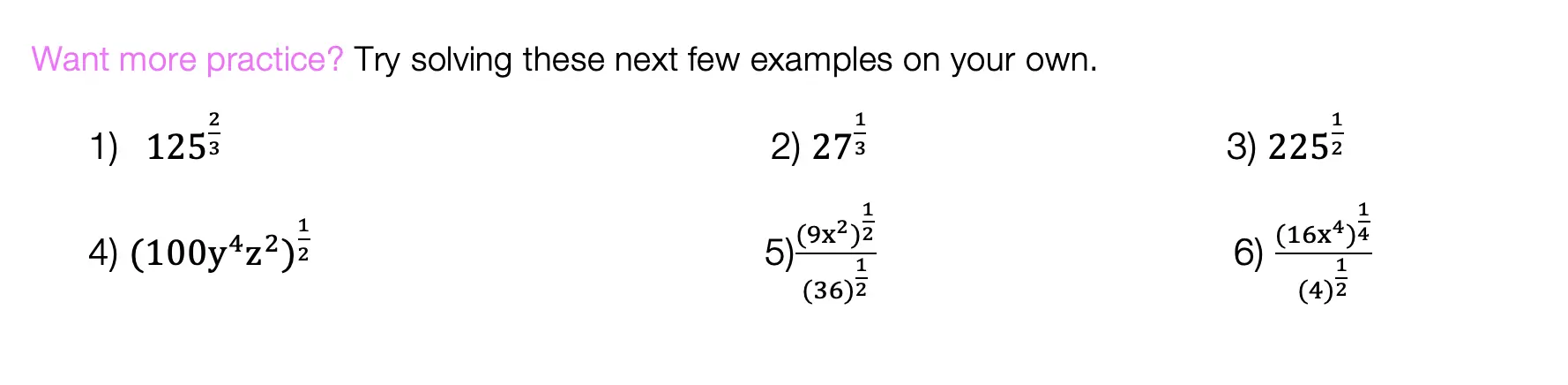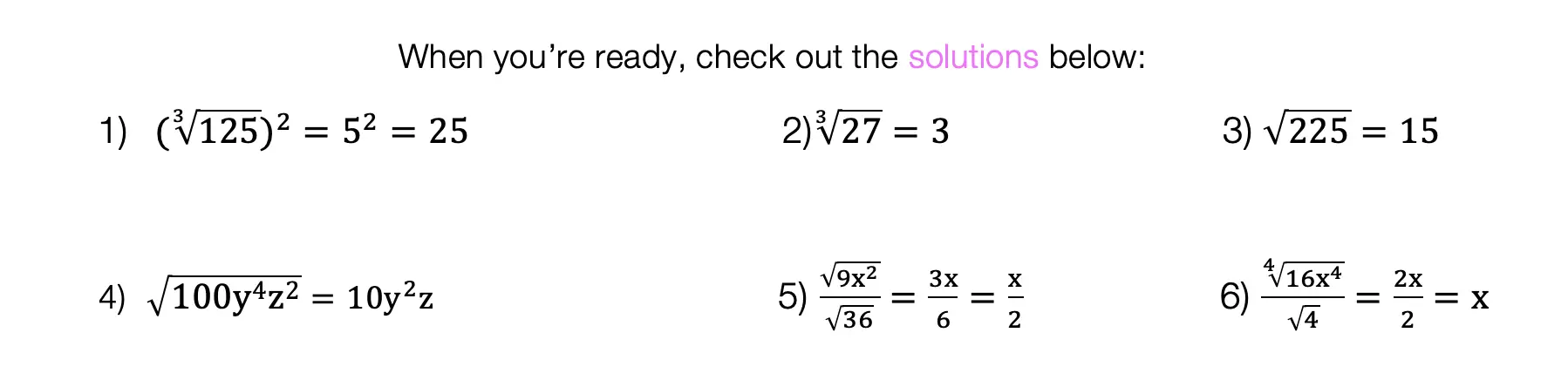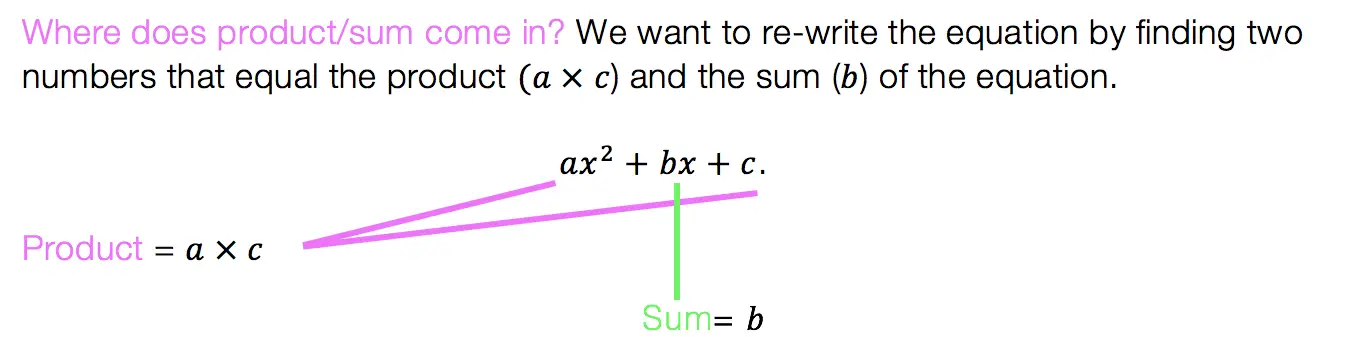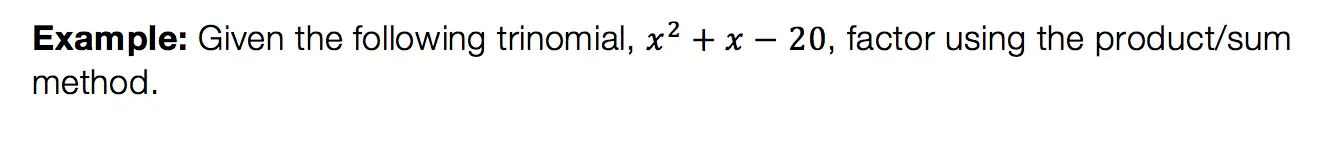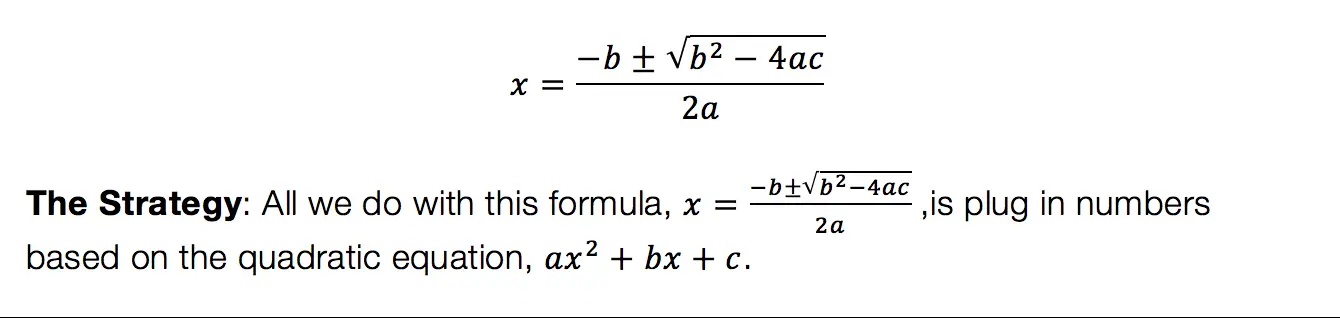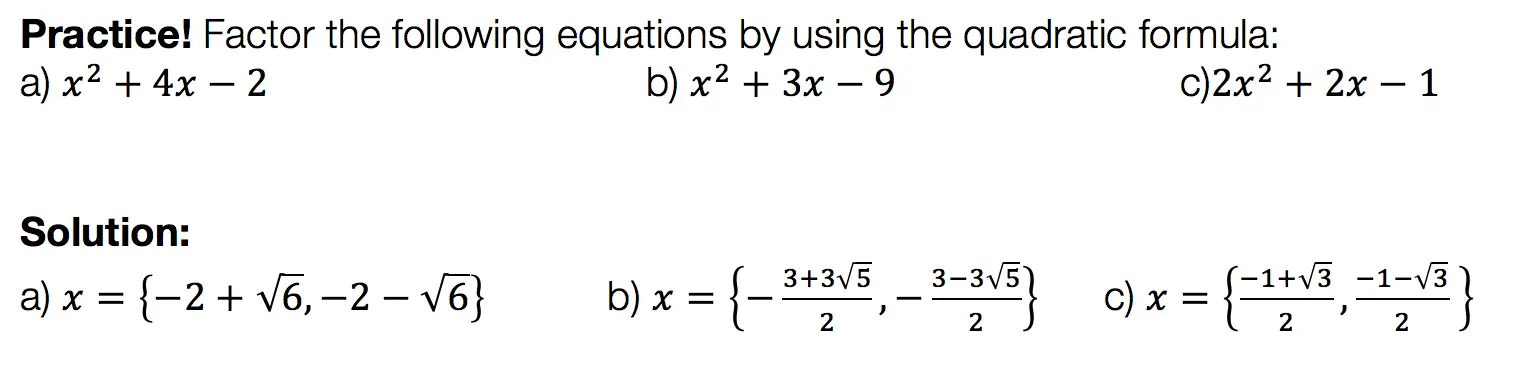Edtech Archives - Page 8 of 9

Binomial Cubic Expansion: Algebra 2/Trig.

Hey math friends! In this post, we are going to go over Binomial Cubic Expansion by going step by step! We’ll start by reviewing an old Regents question. Then, to truly master the topic, try the practice problems at the end of this post on your own! And, if you still have questions, don’t hesitate to watch the video or comment below. Thanks for stopping by and happy calculating! 🙂

Also, if you’re looking for more on Binomial Cubic Expansion, check out this post here!

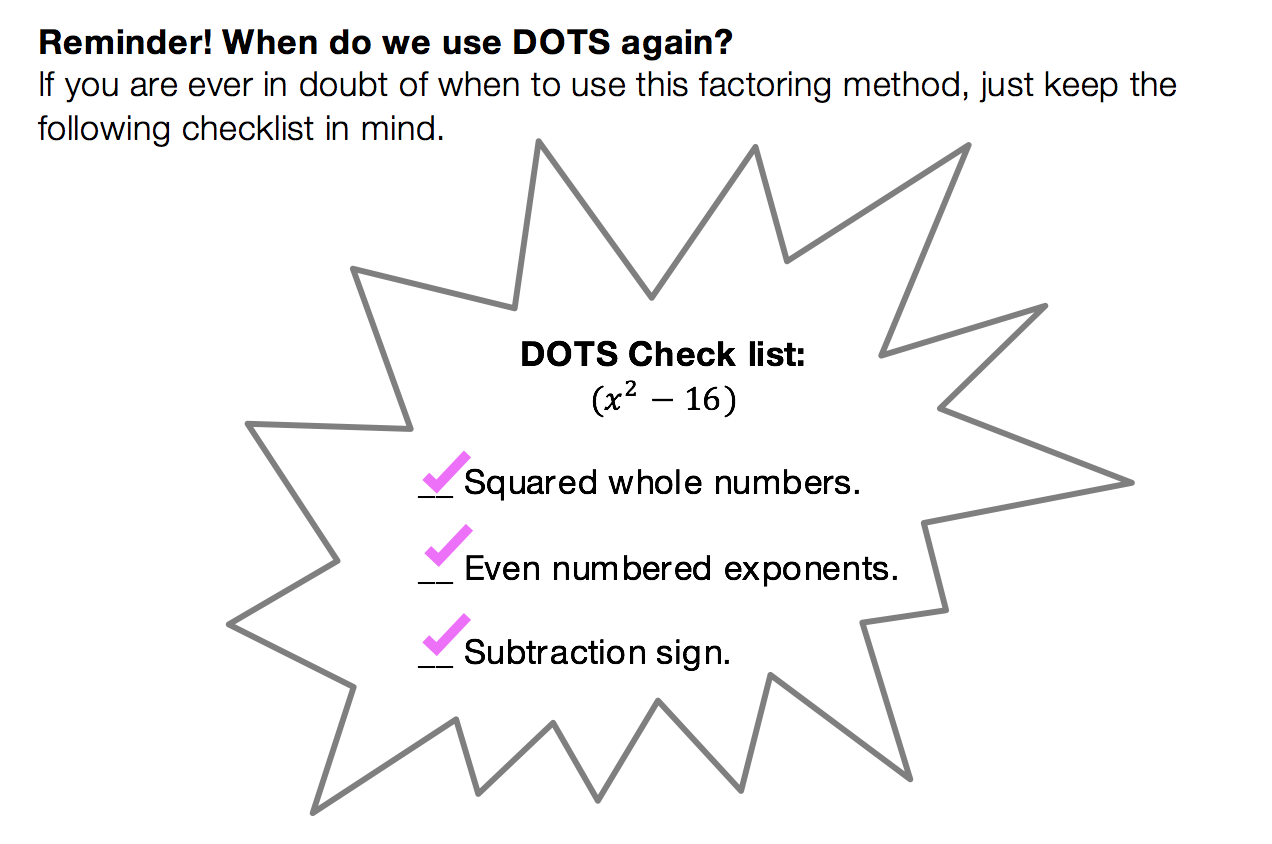
What are Cubed Binomials?

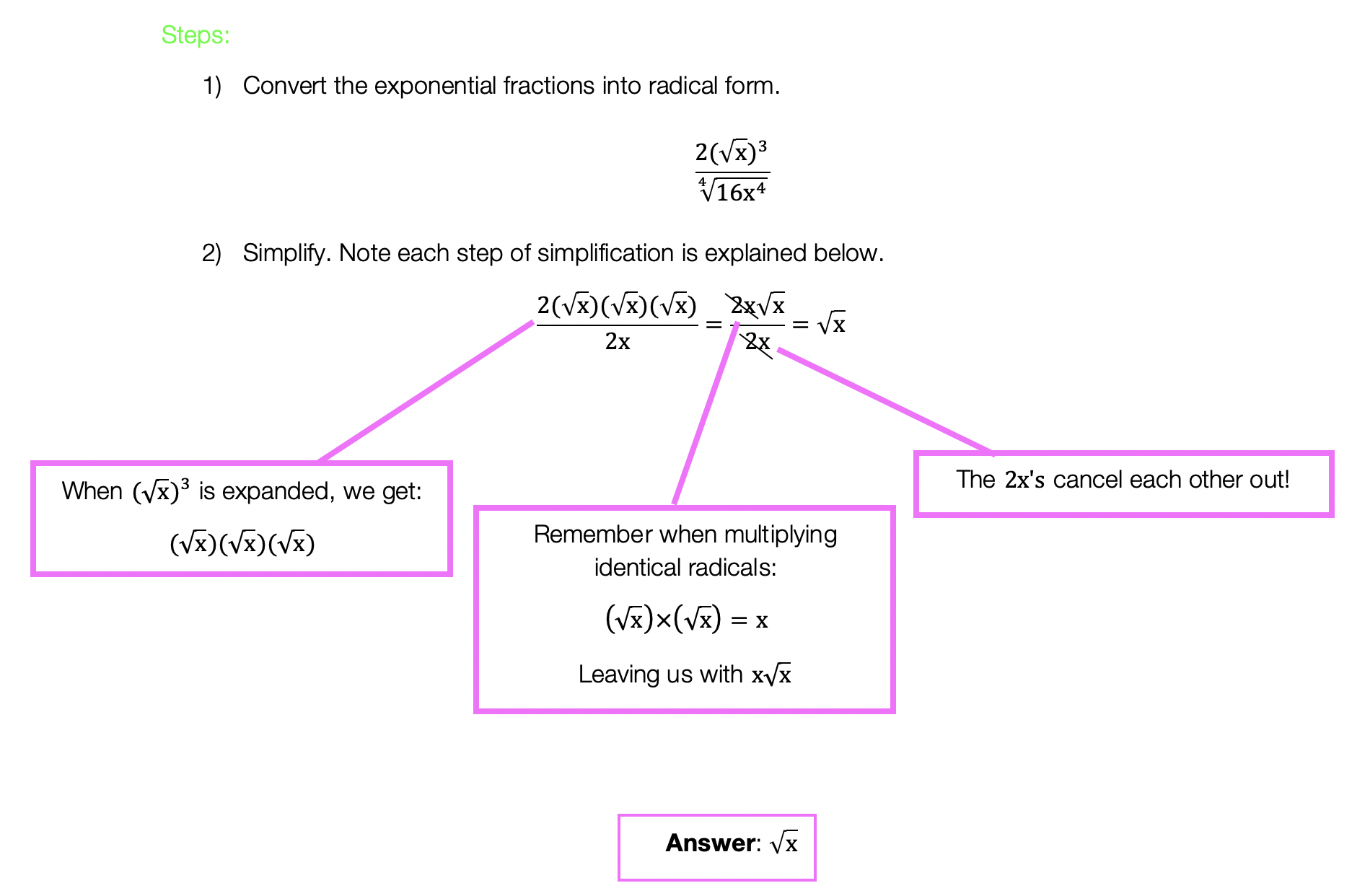
Binomials are two-termed expressions, and now we are cubing them with a triple exponent! See how to tackle these types of problems with the example below:

How do I answer this question?

We need to do an algebraic proof to see if (a+b)³=a³+b³.

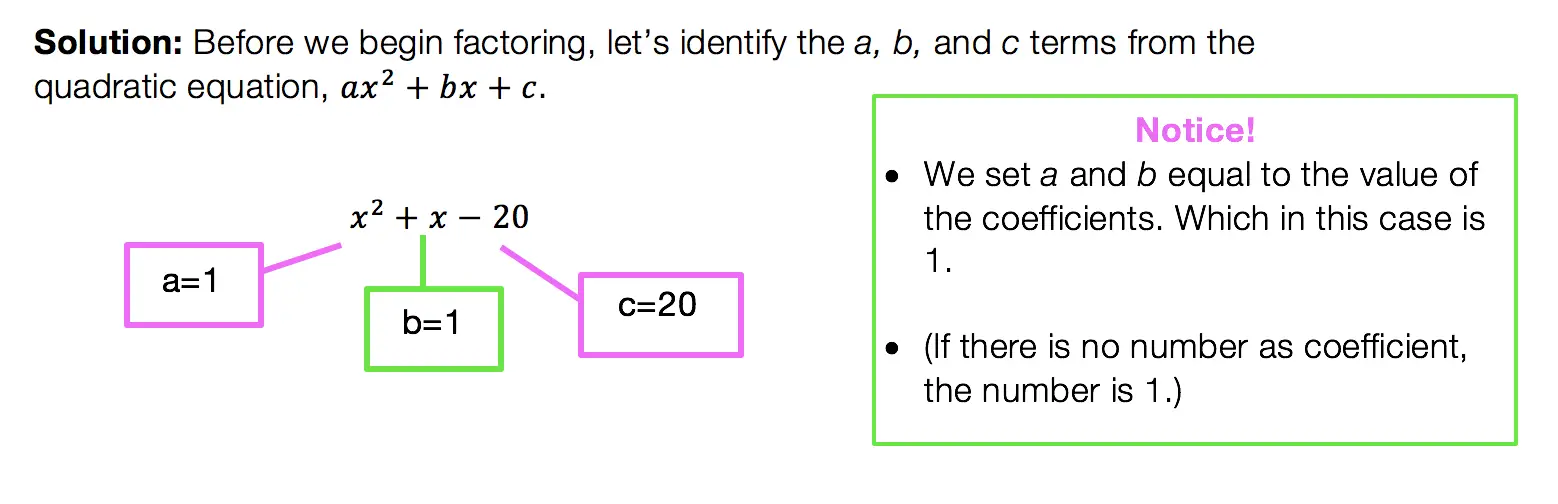
How do we do this?

We set each expression equal to one another, and try to get one side to look like the other by using FOIL and distributing. In this case, we will be expanding (a+b)³ to equal (a+b)(a+b)(a+b).

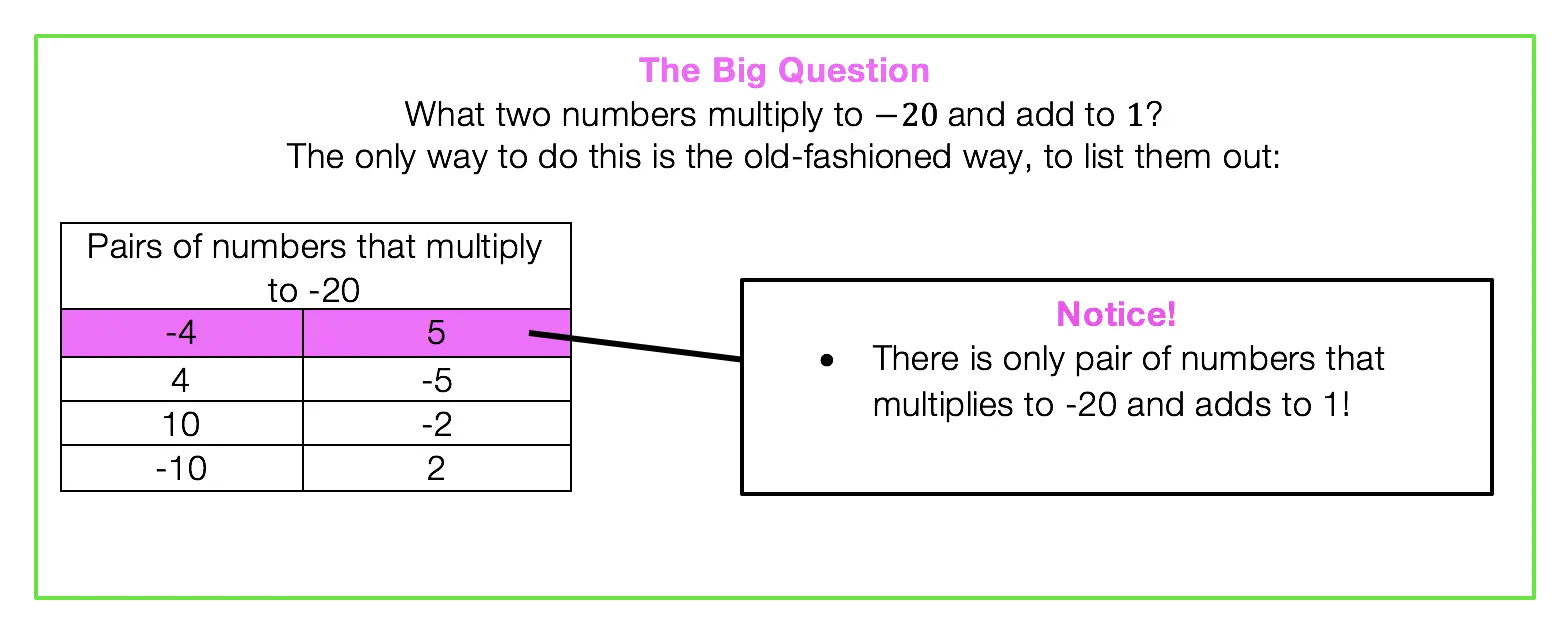
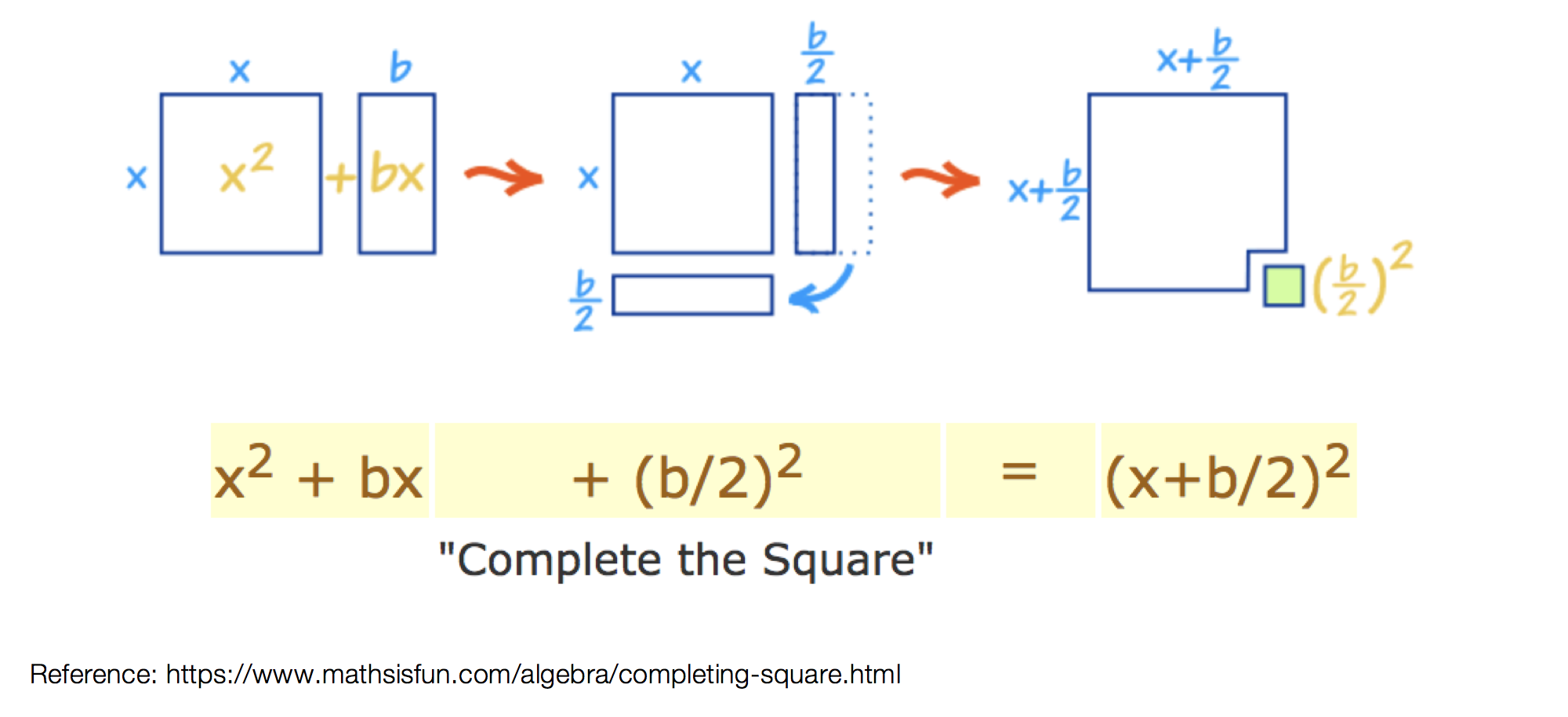
Extra Tip! Notice that we used something called FOIL to combine (a+b)(a+b). But what does that even mean? FOIL is an acronym for multiplying the two terms together. It’s a way to remember to distribute each term to one another. Take a look below:

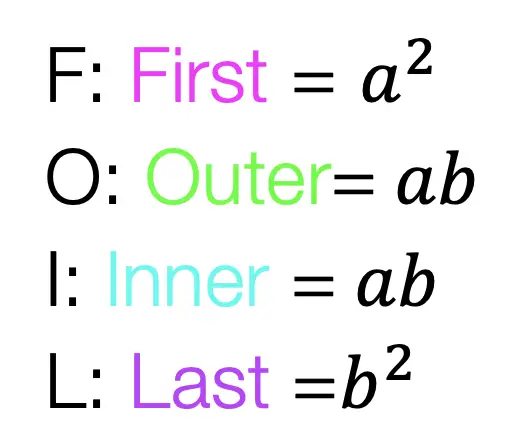
Screen Shot 2019-05-24 at 9.02.50 AM.png

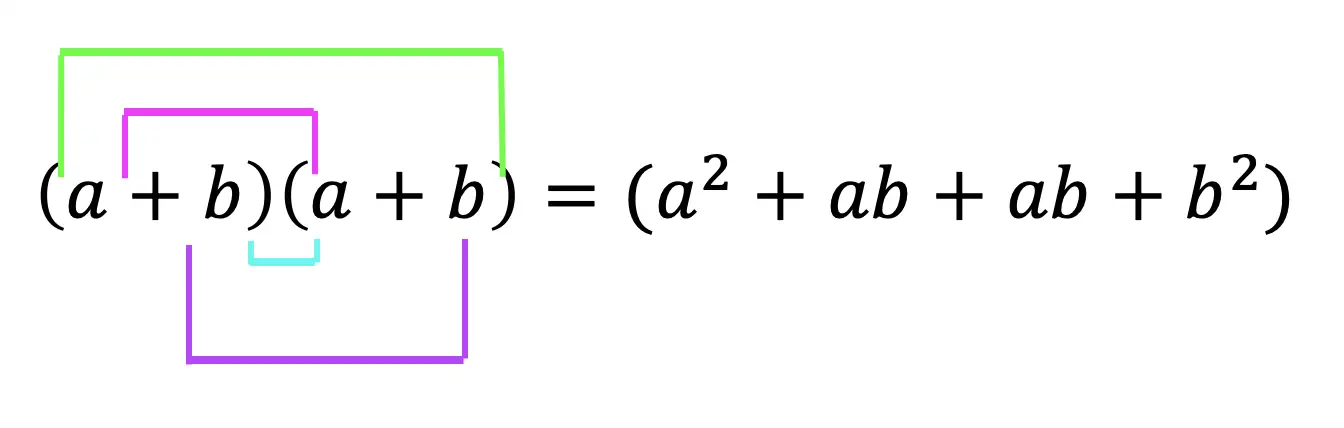
Screen Shot 2019-05-24 at 9.03.23 AM.png

Add and combine all like terms together and we get !

_______________________________________________________________________

Keep in touch with MathSux and get FREE math videos, lessons, and practice questions straight to your inbox! Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Volume of a Cone: Geometry

The Voluminous “Vessel” at Hudson Yards

Calling all NYC dwellers! Have you seen the new structure at Hudson Yards? A staircase to nowhere, this bee-hive like structure is for the true adventurists at heart; Clearly, I had to check it out!

Where does math come in here you say? Well, during my exploration, I had to wonder (as am sure most people do) what is the volume of this almost cone-like structure? It seemed like the best way to estimate the volume here, was to use the formula for the volume of a cone!

What do you think the Volume is?

Volume of a Cone:

I estimated the volume by using the formula of a three-dimensional cone. (Not an exact measurement of the Vessel, but close enough!) .

We can find the radius and height based on the given information above. Everything we need for our formula is right here!

Now that we have our information, let’s fill in our formula and calculate!

Extra Tip! Notice that we labeled the solution with feet cubed , which is the short-handed way to write “feet cubed.” Why feet cubed instead of feet squared? Or just plain old feet? When we use our formula we are multiplying three numbers all measured in feet:

radius X radius X (Height/3)

All three values are measured in feet! –> Feet cubed ()

____________________________________________________________________________________

Did you get the same answer? Did you use a different method or have any questions? Let me know in the comments and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking to apply more math to the real world? Check out this post on the Golden Ratio here!

Rate of Change: Algebra

The rate of change, the rate of motion, the rate of a heartbeat. A chart on a piece of paper as boring as it may seem, can produce some pretty great numbers that directly relate to us human folk.

The question below may make you groan at first glance, but what happens if we use our imagination to picture the real-life bird it’s describing? Any better? Yes? No? Well, either way we must solve, so let’s get to it

How do I answer this question?

It wants us to find the Rate of Change, specifically between 3 and 9 seconds. Let’s hi-light those two values on our given table:

What is the Rate of Change?

To get the Rate of Change between these two values, we need to go back to the good ole’ Slope Formula and realize that the list of values is really a list of x and y coordinates.

Now let’s plug in the coordinate values (3, 6.26) and (9,3.41) into our slope formula:

Extra Tip! Notice that we added the labels feet/second to our answer. Why does this make sense?? The question tells us that P(t) represents feet and that t is equal to seconds. Another way to look at this question when applying it to the slope formula is to realize that we are finding the change of feet divided by the change of seconds. ____________________________________________________________________________________

Still got questions? Let me know in the comments and as always happy calculating!:)

Looking for the next step? Learn how to graph equation of a line, y=mx+b here!

Facebook ~ Twitter ~ TikTok ~ Youtube

Intersecting Secants: Geometry

intersecting secants theorem

Hey math friends! In today’s post, we are going to go over the Intersecting Secants Theorem, specifically using it to find the piece of a missing length on a secant line. We are also going to see proof as to why this theorem works in the first place!

Just a warning: this blog post contains circles. This usually non-threatening shape can get intimidating when secants, chords, and tangents are involved. Luckily, this question is not too complicated and was also spotted on the NYS Regents. Before looking at the questions below, here is a review on different parts of a circle. Pay close attention to what a secant is, which is what we’ll be focusing on today:

Think you are ready? Let’s look at that next question!

What information do we already have? Based on the question we know:

Screen Shot 2018-12-25 at 12.54.24 PM.png

*Extra Tip! Why does this formula work in the first place!?? If we draw lines creating and proving triangle RTQ and triangle RPS are similar by AA, this leads us to know that the two triangles have proportionate sides and can follow our formula! ___________________________________________________________________________________

Still got questions? Let me know in the comments and remember having questions is a good thing!

If you’re looking for more on intersecting secants, check out this post here for practice questions and more!

Facebook ~ Twitter ~ TikTok ~ Youtube

Rational Exponents: Algebra 2/Trig.

Hi everyone and welcome to MathSux! In this post we are going to break down and solve rational exponents. The words may sound like a mouthful, but all rational exponents are, are fractions as exponents. So instead of having x raised to the second power, such as x², we might have x raised to the one-half power, such as x^(1/2). Let’s try an example taken straight from the NYS Regents below. Also, if you have any questions don’t hesitate to comment below or check out the video posted here. Happy calculating! 🙂

How do I answer this question?

The questions want us to simplify the rational exponents into something we can understand.

How do we do this?

We are going to convert the insane looking rational exponents into radical and solve/see if we can simplify further.

Reminder!

A radical can be converted into a rational exponent and vice versa. Not sure what that means? It’s ok! Take a gander at the examples below and look for a pattern:

Think you’re ready to take on our original problem? #Letsdothis

Example:

Screen Shot 2018-12-16 at 2.21.06 PM.png

Practice:

Solutions:

Screen Shot 2018-12-16 at 2.20.42 PM.png

Still got questions? Don’t hesitate to comment below for anything that still isn’t clear! Looking to review how to solve radical equations? Check out this post here! 🙂

Also, don’t forget to follow MathSux fopr FREE math videos, lessons, practice questions and more every week!

Facebook ~ Twitter ~ TikTok ~ Youtube

The Magic of the “Golden Ratio”

Walking around NYC, I was on a mission to connect mathematics to the real world. This, of course, led me to go on a mathematical scavenger hunt in search of the “Golden Ratio.” Hidden in plain sight, this often times naturally occurring ratio is seen everywhere from historic and modern architecture to nature itself.

What is this all-encompassing “Golden Ratio” you may ask?
It’s a proportion, related to a never-ending sequence of numbers called the Fibonacci sequence, and is considered to be the most pleasing ratio to the human eye. The ratio itself is an irrational number equal to 1.618……..(etc.).

Why should you care?
When the same ratio is seen in the Parthenon, the Taj Mahal, the Mona Lisa and on the shores of a beach in a seashell, you know it must be something special!
The Golden Ratio

Random as it may seem, this proportion stems from the following sequence of numbers, known as the Fibonacci sequence:

1, 1, 2, 3, 5, 8, 13, 21, …….

Do you notice what pattern these numbers form?
(Answer: Each previous two numbers are added together to find the next number.)

The Golden Rectangle: The most common example of the “Golden Ratio” can be seen in the Golden rectangle. The lengths of this rectangle are in the proportion from 1: 1.618 following the golden ratio. Behold the beauty of the Golden Rectangle:

How is the Fibonacci Sequence related to the Golden Ratio? What if we drew a golden rectangle within our rectangle?

Then drew another golden rectangle within that golden rectangle?

And we kept doing this until we could no longer see what we were doing…….

The proportion between the width and height of these rectangles is 1.618 and can also be shown as the proportion between any two numbers in the Fibonacci sequence as the sequence approaches infinity. Notice that the area of each rectangle in the Fibonacci sequence is represented below in increasing size:

Where exactly can you find this Golden Ratio in real life? Found in NYC! The Golden ratio was seen here at the United Nations Secretariat building in the form of a golden rectangle(s). Check it out!

Where have you seen this proportion of magical magnitude? Look for it in your own city or town and let me know what you find! Happy Golden Ratio hunting! 🙂

If you’re interested in learning more about the golden ratio and are also a big Disney fan, I highly recommend you check out Donald Duck’s Math Magic!

Don’t forget to connect with MathSux on these great sites!

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking to learn more about math phenomenons found in the real world? Check out this article on fractals! And if you want to learn about more sequences, check out the link here!

How to Factor Quadratic Equations: Algebra

In this post, we are going to dive deep into how to factor Quadratic equations! There are so many different methods to choose from including GCF, Product/Sum, DOTS, and the Quadratic Formula. Here we will go step by step into each method on how to factor quadratic equations, each with their own set of practice questions. For a review on how to factor by grouping, check out this post here and happy calculating! 🙂

Why factor in the first place, you may say? We want to manipulate the equation until we solve for x. Solving for x is our main goal, and factoring allows us to do that. Now let’s get to the good stuff!

How to factor quadratic equations

Greatest Common Factor (GCF):

The greatest common factor is the highest possible number that can be divided out from an equation. This gets the equation into its simplest form and makes it easier for us to solve for x.

Before considering which type of factoring methdo to use, always ask yourself, “Can I take out a GCF?”

How to factor quadratic equations

Product/Sum:

This factoring method is for quadratic equations only! That means the equation takes on the following form:

How to factor quadratic equations

Difference of Two Squares DOTS)

Not to play favorites or anything, but DOTS is the easiest and most lovable of the factoring methods. This factoring method just makes you feel all warm and fuzzy inside or maybe that’s just me). Before we get into how to do DOTS, let’s talk about when?

Quadratic Formula:

We have heard of the quadratic equations, so how id the quadratic formula different?

The Answer: The Quadratic Formula is what we use to factor any trinomial. You can use product/sum on trinomials like we discussed earlier, but this may not always work out easy. The Quadratic Formila on the other hand will work every time!

Low and behold, the Quadratic Formula:

Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Quadratic Equations with 2 Imaginary Solutions

Imaginary and Complex Numbers

Focus and Directrix of a Parabola

Facebook ~ Twitter ~ TikTok ~ Youtube

‘Math Suks’ ~ Jimmy Buffett

Need to relax after studying? Close to wanting to “burn your textbook”? This super chill and somewhat cheesy song may help! Coming to you from Jimmy Buffett, the singer has a relaxed, island/ska like vibe to his music. The lyrics come close to sounding like an after school special until the words “Math Sucks” are sung over and over again. Enjoy! 🙂

Click here to listen to the song:

‘Math Suks’ by Jimmy Buffet Lyrics:

If necessity is the mother of invention
Then I’d like to kill the guy who invented this
The numbers come together in some kind of a third dimension
A regular algebraic bliss.

Let’s start with something simple, like one and one ain’t three
Any two plus two will never get you five.
There are fractions in my subtraction and x don’t equal y
But my homework is bound to multiply.

Math suks math suks
I’d like to burn this textbook, I hate this stuff so much.
Math suks math suks
Sometimes I think that I don’t know that much
But math suks.

I got so bored with my homework, I turned on the TV.
The beauty contest winners were all smiling through their teeth.
Then they asked the new Miss America
Hey babe can you add up all those bucks?
She looked puzzled, then just said
“Math Suks”.

Math suks math suks
You don’t even have to spell it,
All you have to do is yell it…
Math suks math suks
Sometime times I think that I don’t know that much
But math suks.

Geometry, trigonometry and if that don’t tax your brain
There are numbers to big to be named
Numerical precision is a science with a mission
And I think it’s gonna drive me insane.

Parents fighting with their children, and the Congress can’t agree
Teachers and their students are all jousting constantly.
Management and labor keep rattling old sabers
Quacking like those Peabody ducks.

Math suks math suks
You don’t even have to spell it,
All you have to do is yell it…
Math suks math suks
Sometime times I think that I don’t know that much
But math suks

Why Must We Complete the Square?: Algebra

Completing the Square: So many steps, such little time. It sounds like it involves a square or maybe this is a geometry problem? Why am I doing this again? Why must we complete the square in the first place?

These are all the thoughts that cross our minds when first learning how to complete the square. Well, I’m here to tell you there is a reason for all those steps and they aren’t that bad if you really break them down, let’s take a look!

Answer: x={-7,3}

Explanation:

I’m not going to lie to you here, there are a lot of seemingly meaningless steps to completing the square. The truth is though (as shocking as it may be), is that they are not meaningless, they do form a pattern, and that there is a reason! Before we dive into why let’s look at how to solve this step by step:

Feeling accomplished yet!? Confused? All normal feelings. There are many steps to this process so go back and review, practice, and pay close attention to where things get fuzzy.

But the big question is why are we doing these steps in the first place? Why does this work out, to begin with?

For those of you who are curious, continue to read below!

Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating!

Need more of an explanation? Check out why we complete the square in the first place here !

Facebook ~ Twitter ~ TikTok ~ Youtube

Geometry: Congruent Triangles

Screen Shot 2017-07-27 at 10.07.39 AM

screen-shot-2016-09-12-at-3-47-06-pm

screen-shot-2016-09-12-at-3-48-09-pm

screen-shot-2016-09-12-at-3-49-17-pm

Not bad, eh? If there is anything you have questions on please don’t hesitate to ask! 🙂 If you are looking to test out your skills on this topic even more, check out more challenging questions here.

And for more of me and my nerdy math jokes take a look at MathSux on

Twitter and Facebook. Happy calculating! 🙂