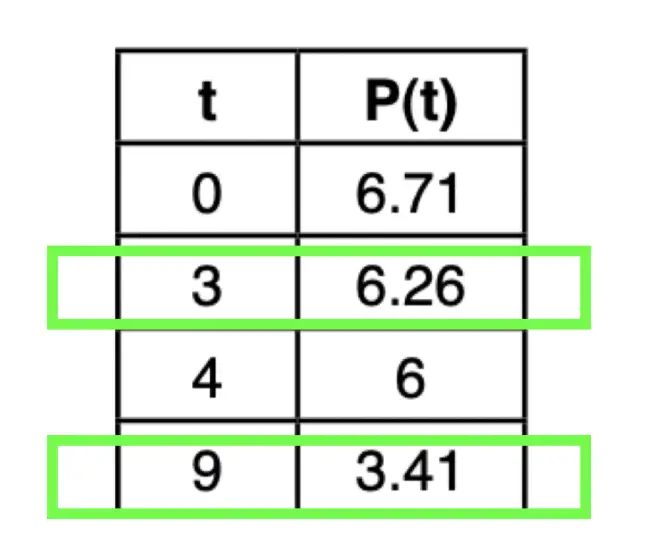
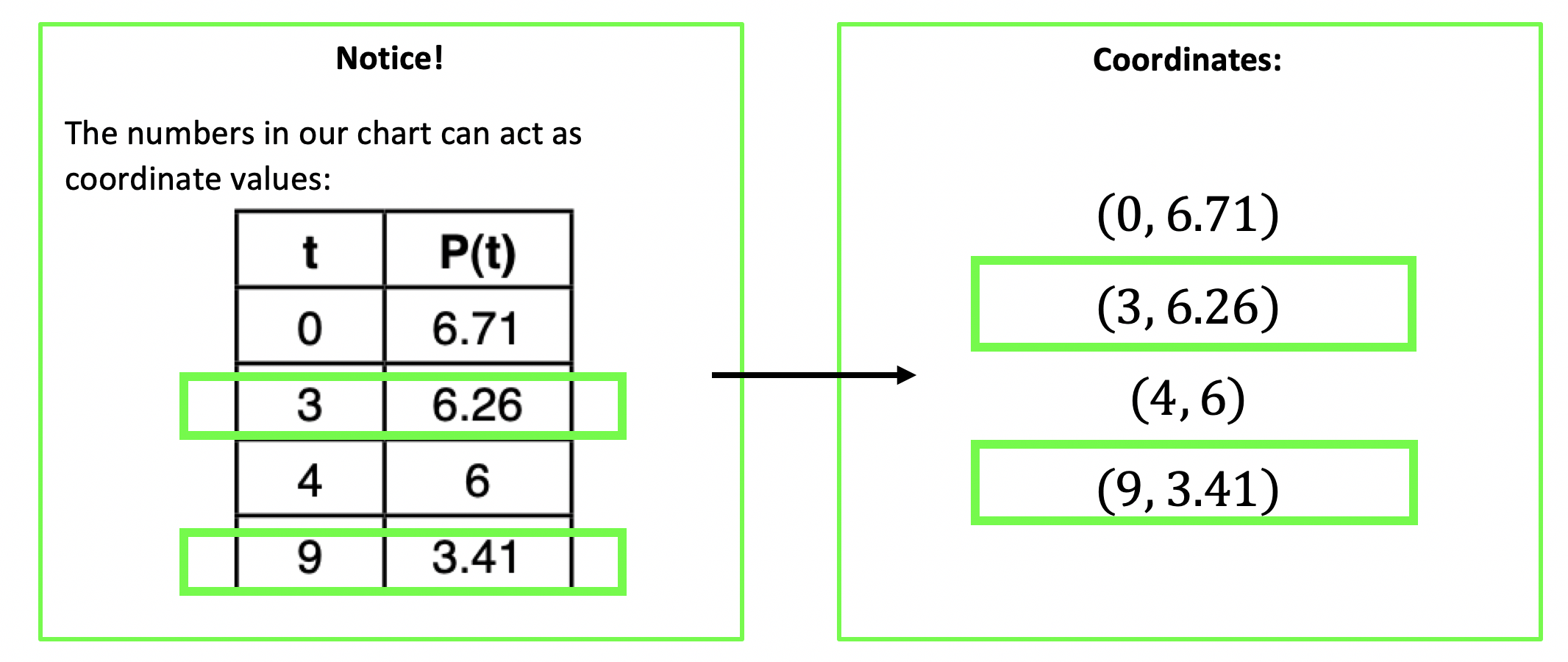
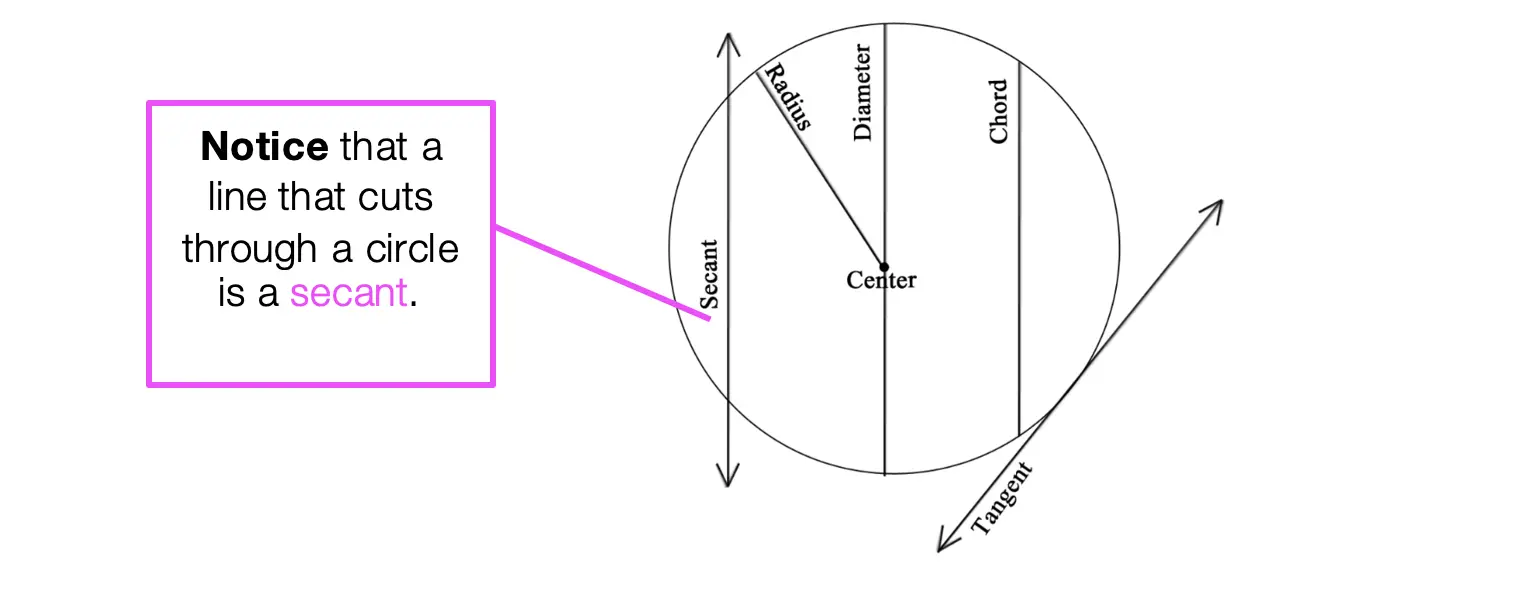
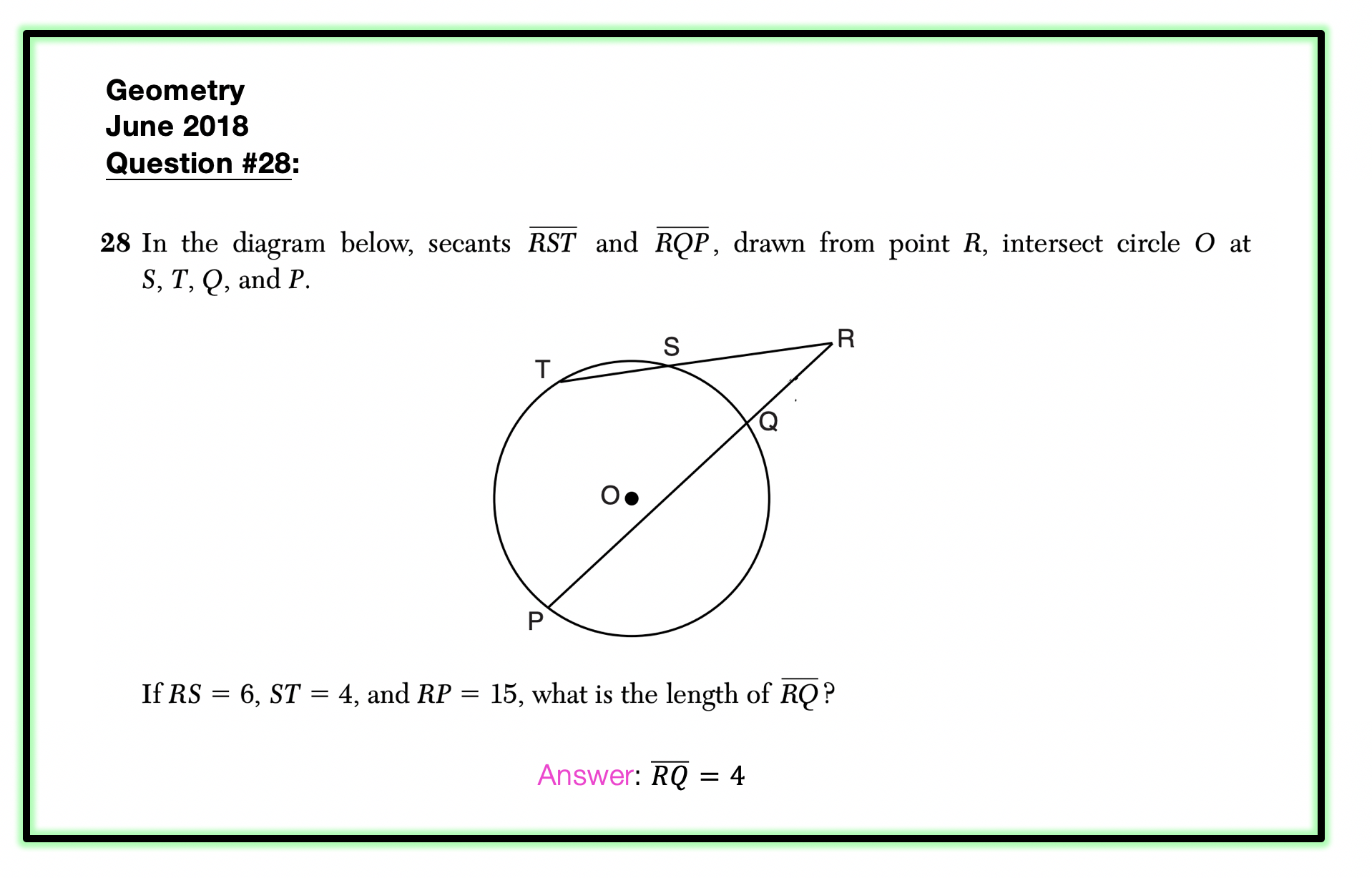
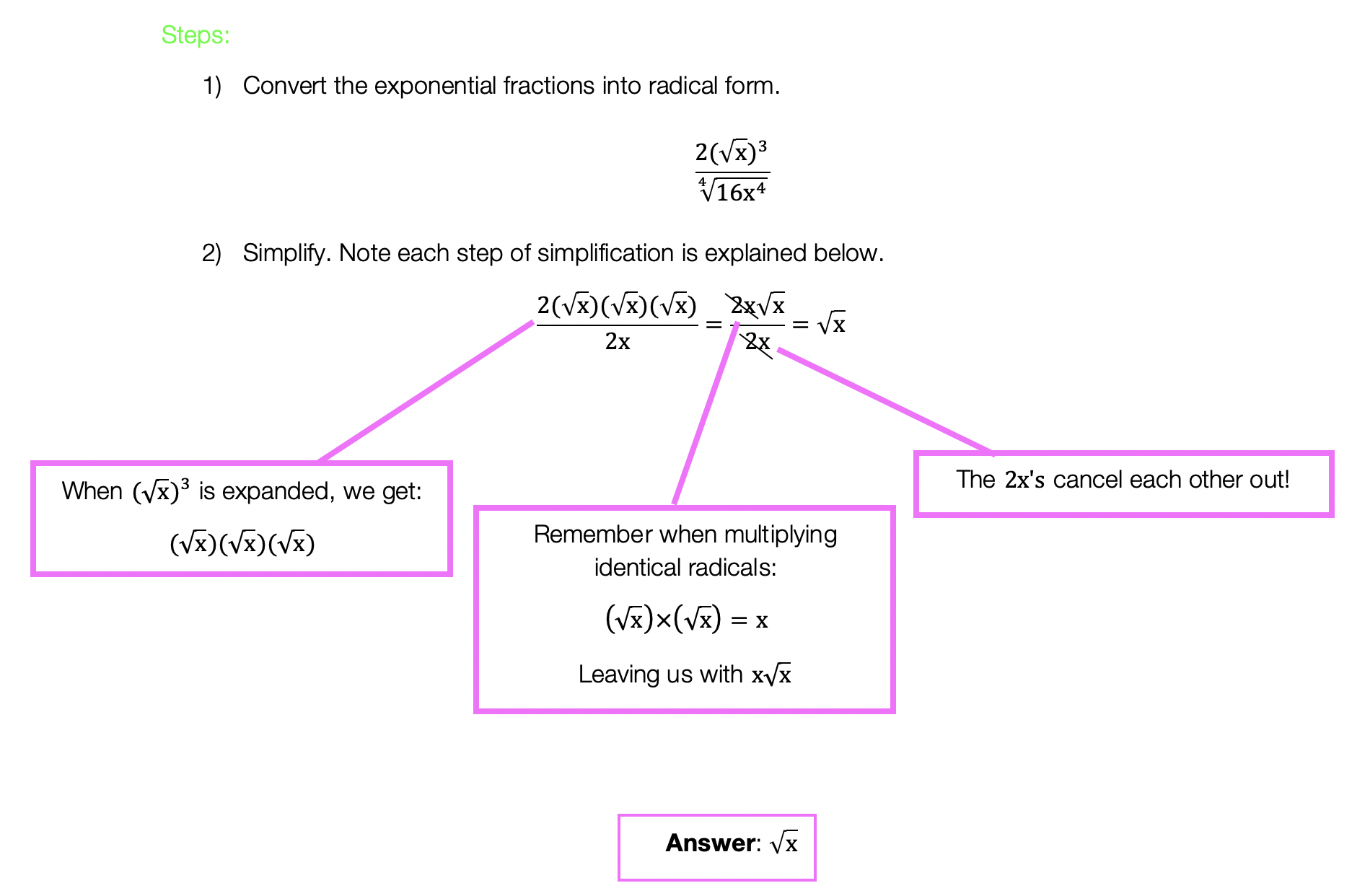
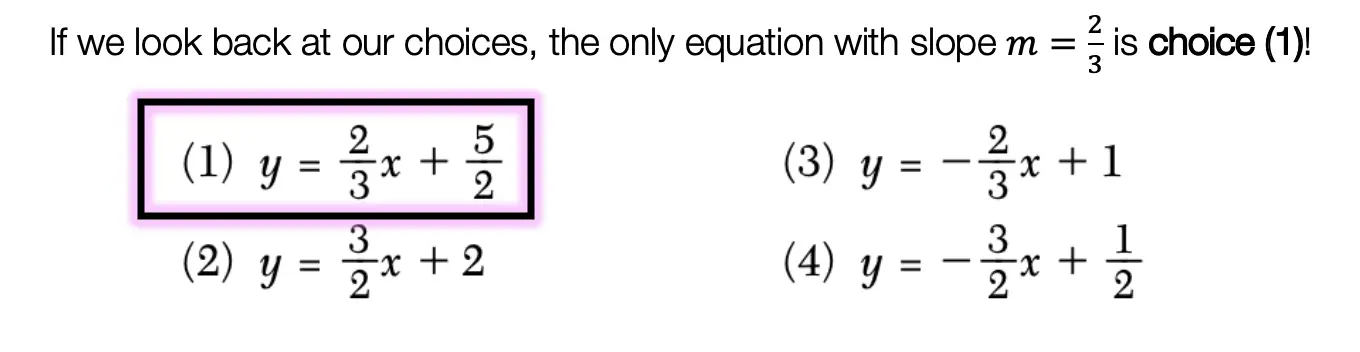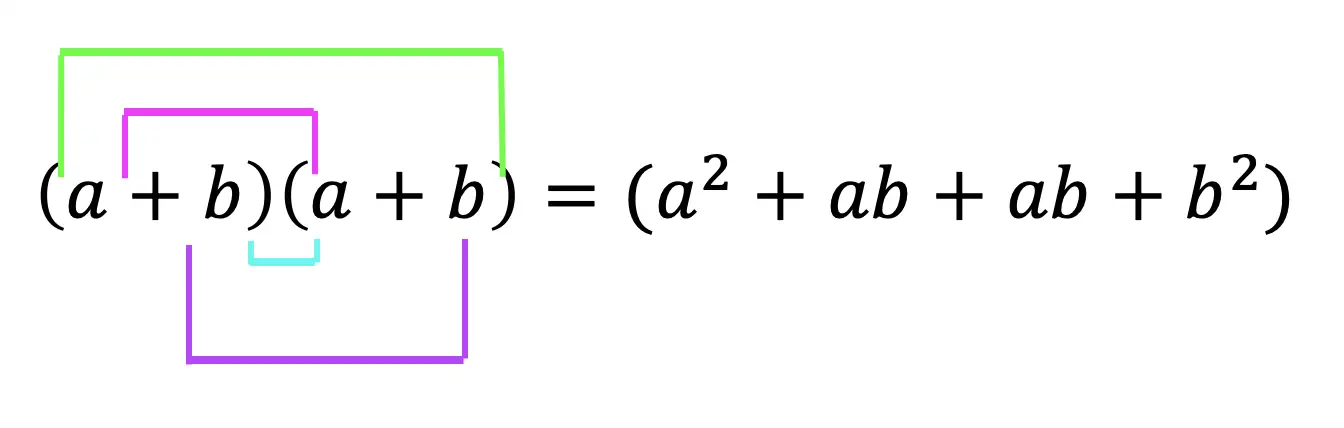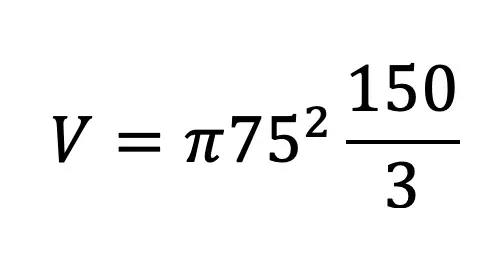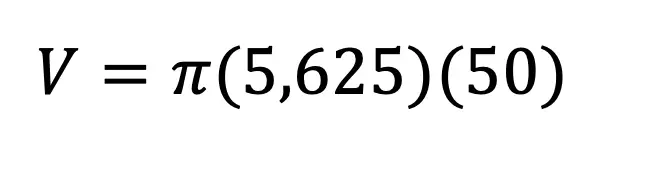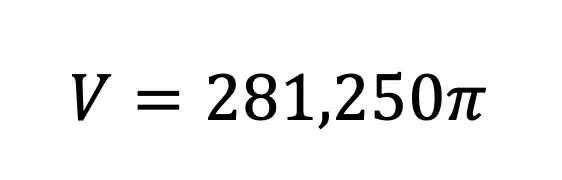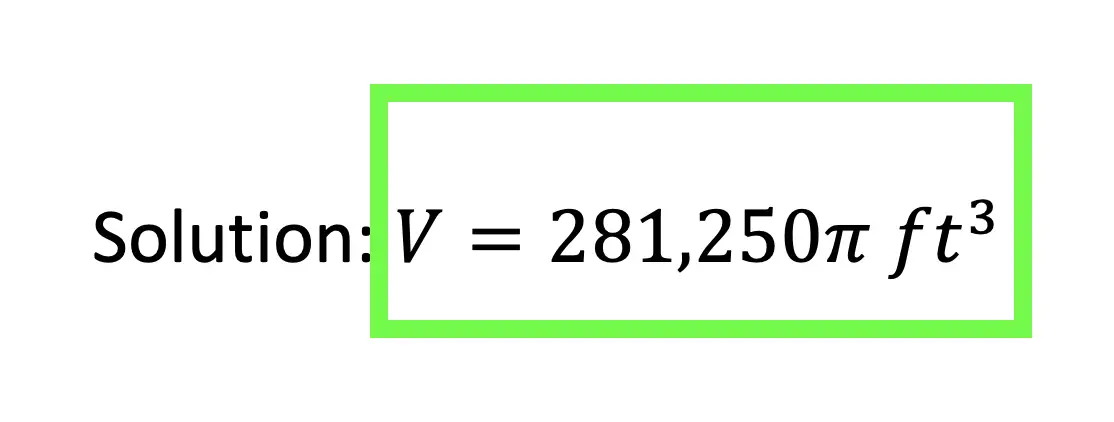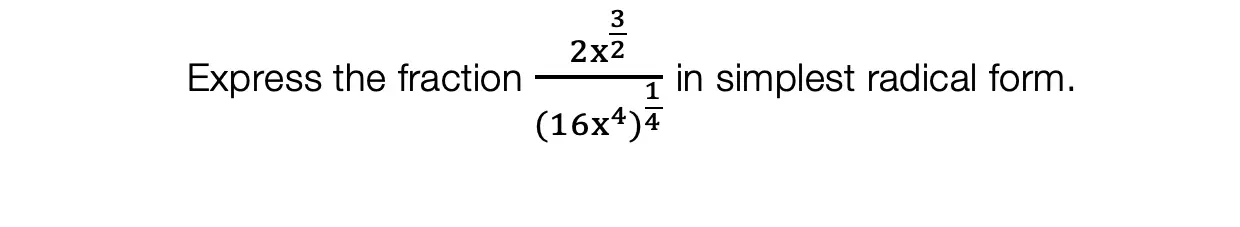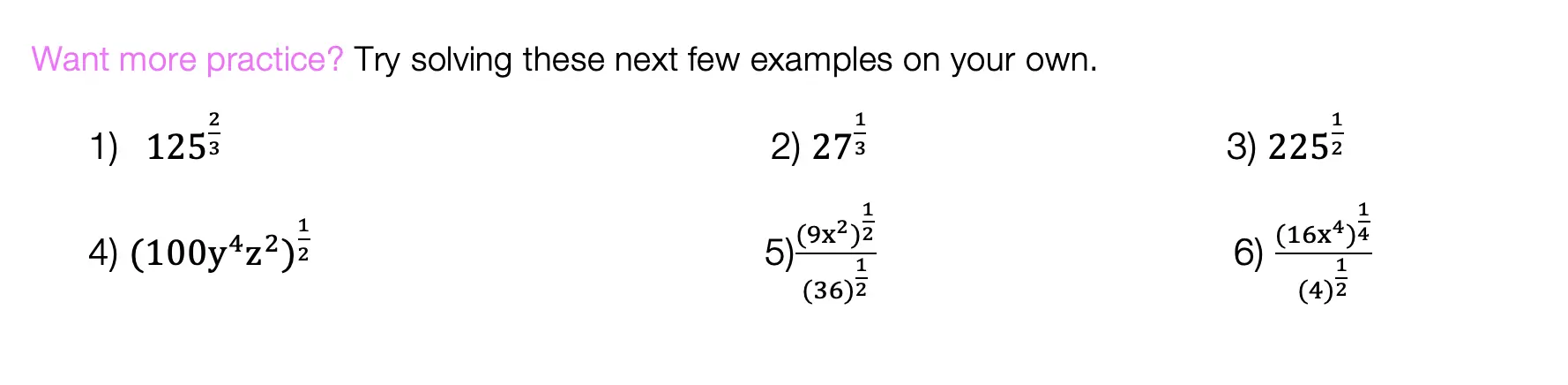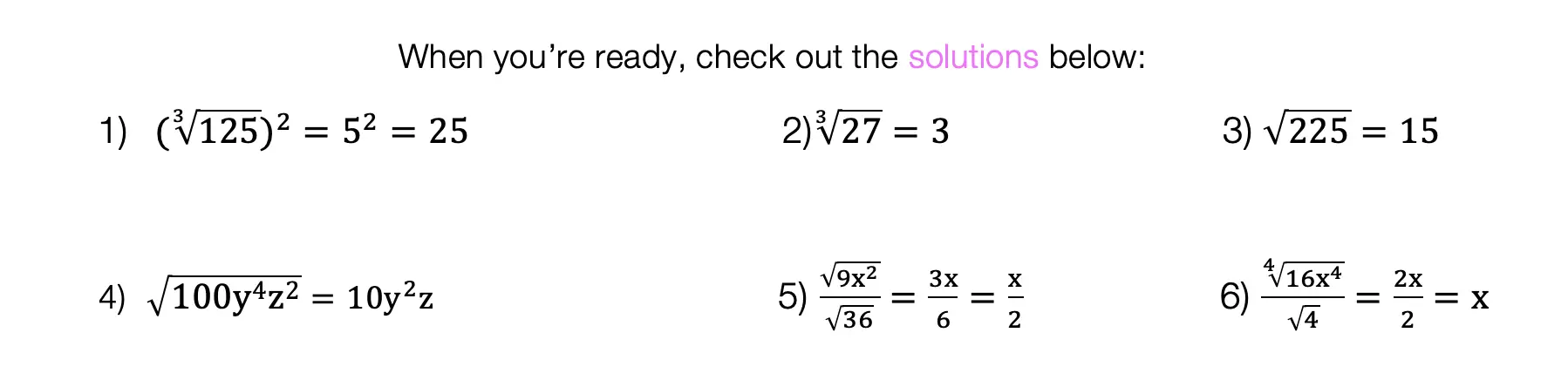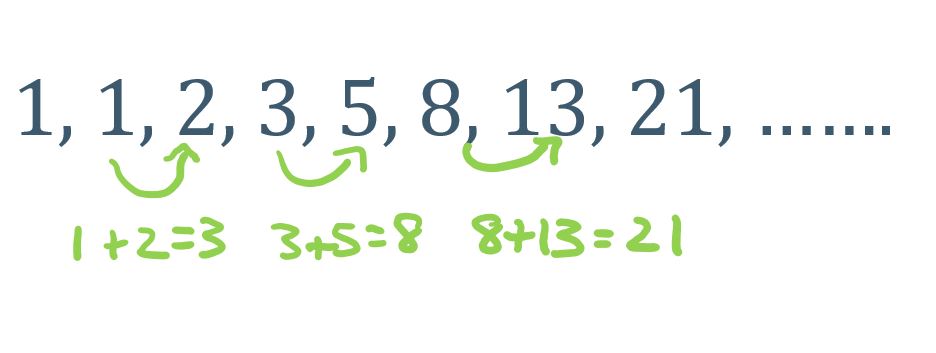In honor of Earth Day last week, I thought we’d take a look at some math that appears magically in nature. Math? In nature? For those of you who think math is unnatural or just terrible in general, this is a great time to be proven otherwise!
The key that links math to nature is all about PATTERNS. All math is based on is patterns. This includes all types of math, from sequences to finding x, each mathematical procedure follows some type of pattern. Meanwhile back in the nearest forest, patterns are occurring everywhere in nature.
The rock star of all patterns would have to be FRACTALS. A Fractal is a repeating pattern that is ongoing and has different sizes of the exact same thing! And the amazing thing is that we can actually find fractals in our neighbor’s local garden.
Let’s look at some Fractal Examples:
(1) Romanesco Broccoli: Check out those repeating shapes, that have the same repeating shapes on those shapes and the same repeating shapes on even smaller shapes and…. my brain hurts!
(2) Fern Leaves: The largest part of this fractal is the entire fern leaf itself. The next smaller and identical part is each individual “leaf” along the stem. If you look closely, the pattern continues!
(3) Leaves: If you’ve ever gotten up real close to any type of leaf, you may have noticed the forever repeating pattern that gets smaller and smaller. Behold the power and fractal pattern of this mighty leaf below!
 .
. 
Just in case fractals are still a bit hard to grasp, check out the most famous Fractal below, otherwise known as Sierpinski’s Triangle. This example might not be found in your local back yard, but it’s the best way to see what a fractal truly is up close and infinite and stuff.


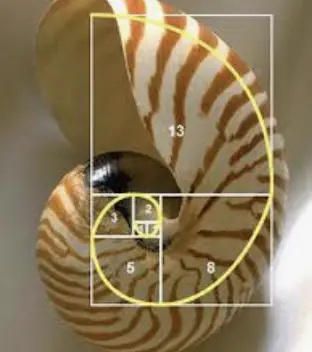
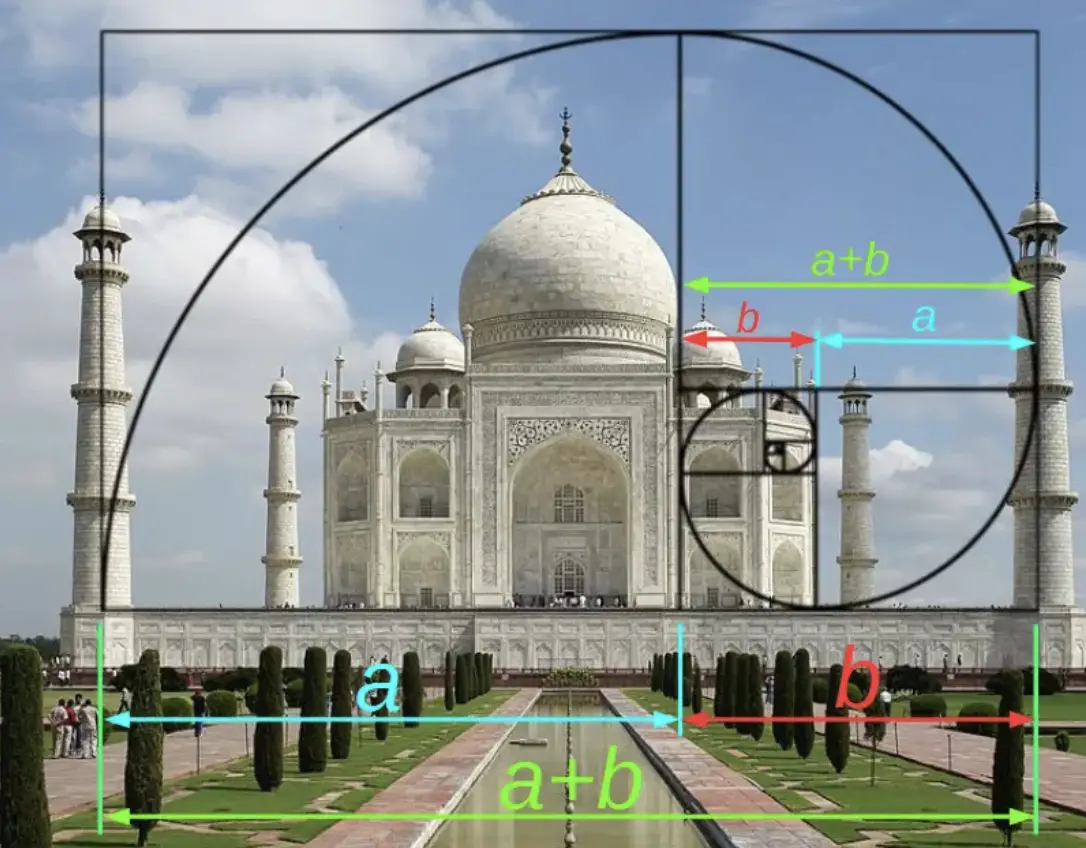
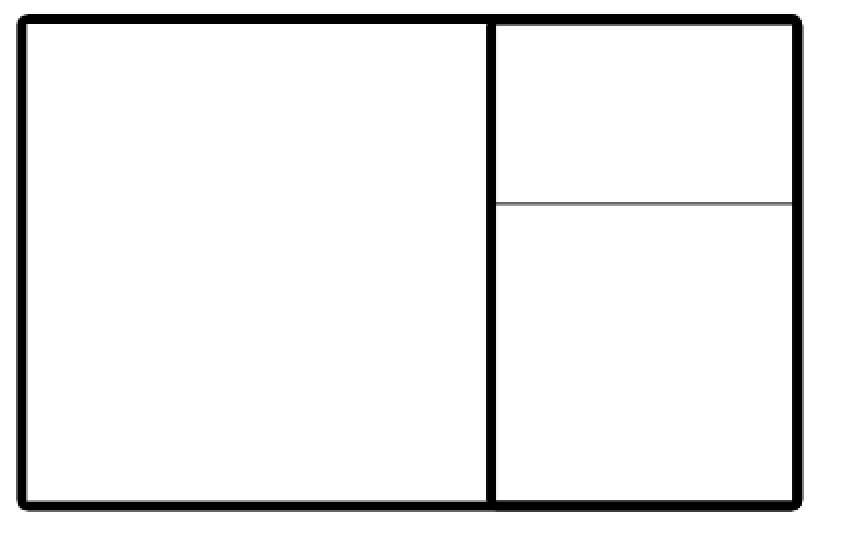
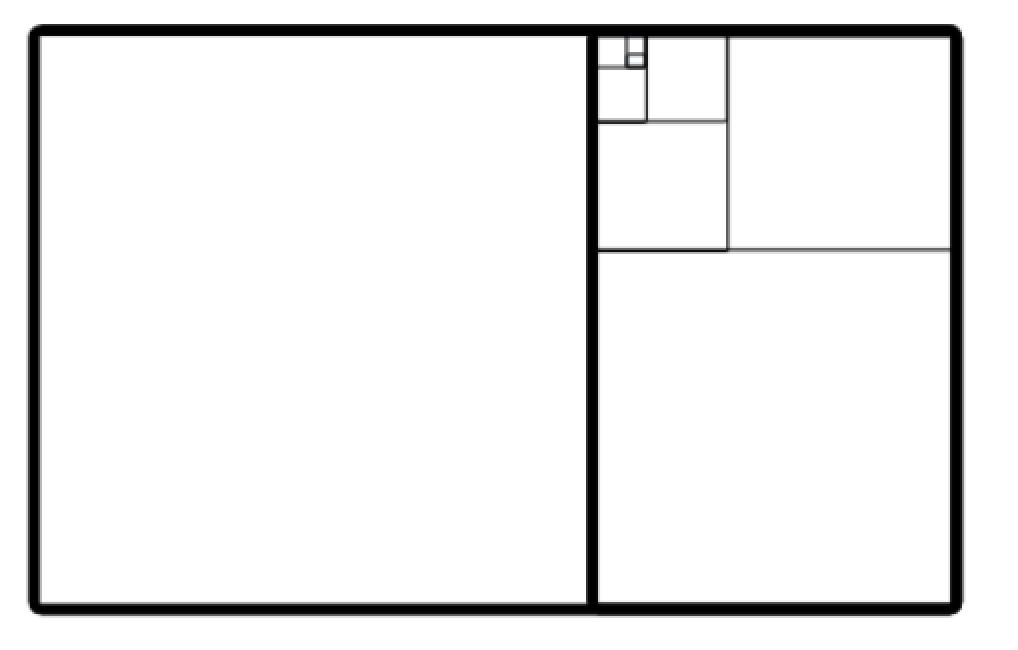
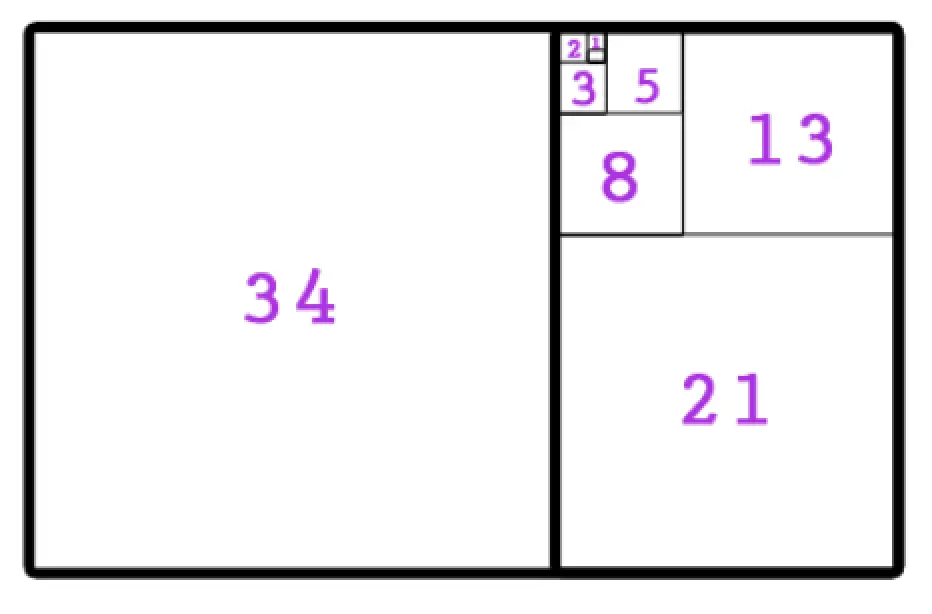
Looking for more math in nature? Check out this post on the Golden Ratio and happy calculating! 🙂