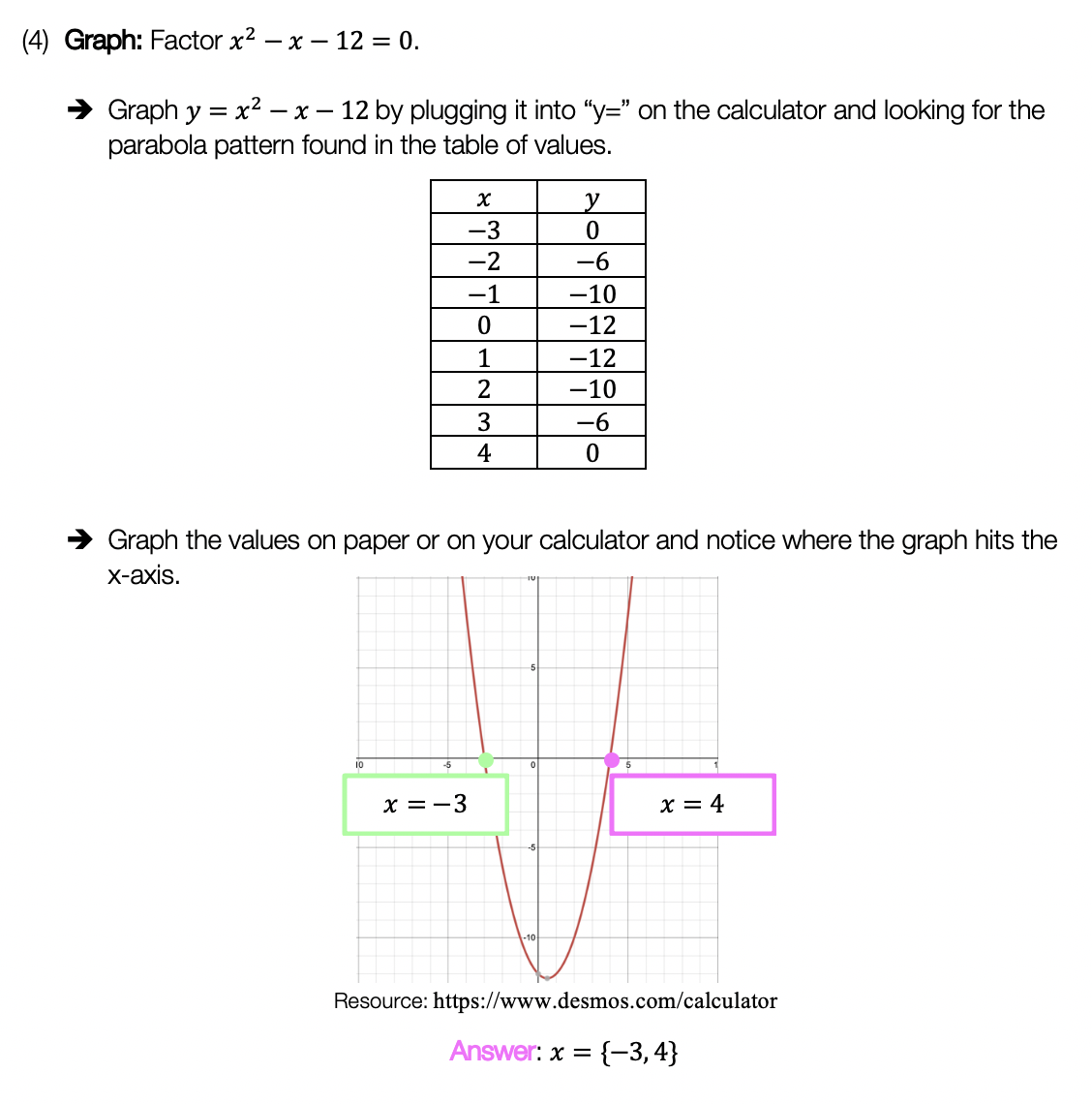
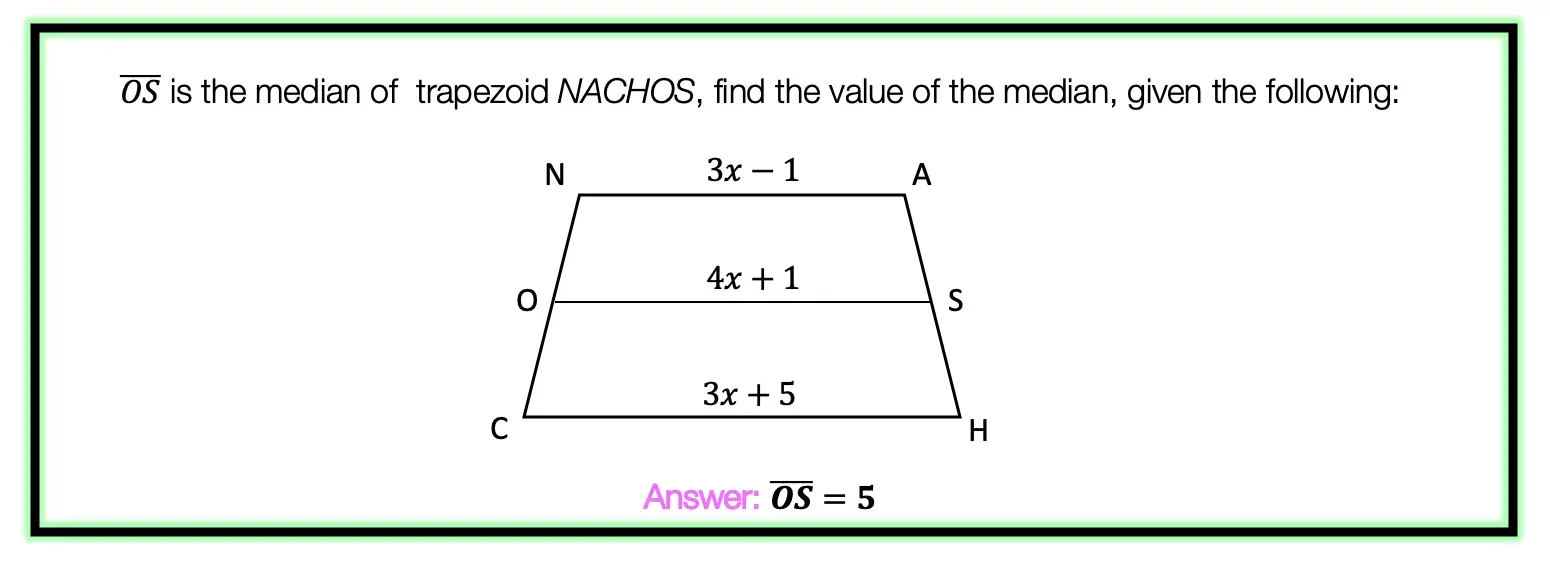
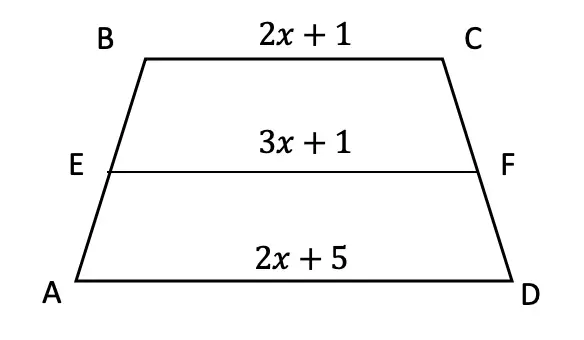
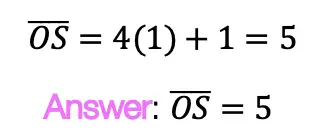Resources Archives - Math Lessons

Piecewise Functions: Algebra

Greetings, today’s post is for those in need of a piecewise functions review! This will cover how to graph each part of that oh so intimidating piecewise functions. There’s x’s, there are commas, there are inequalities, oh my! We’ll figure out what’s going on here and graph each part of the piecewise-function one step at a time. Then check yourself with the practice questions at the end of this post. Happy calculating! 🙂

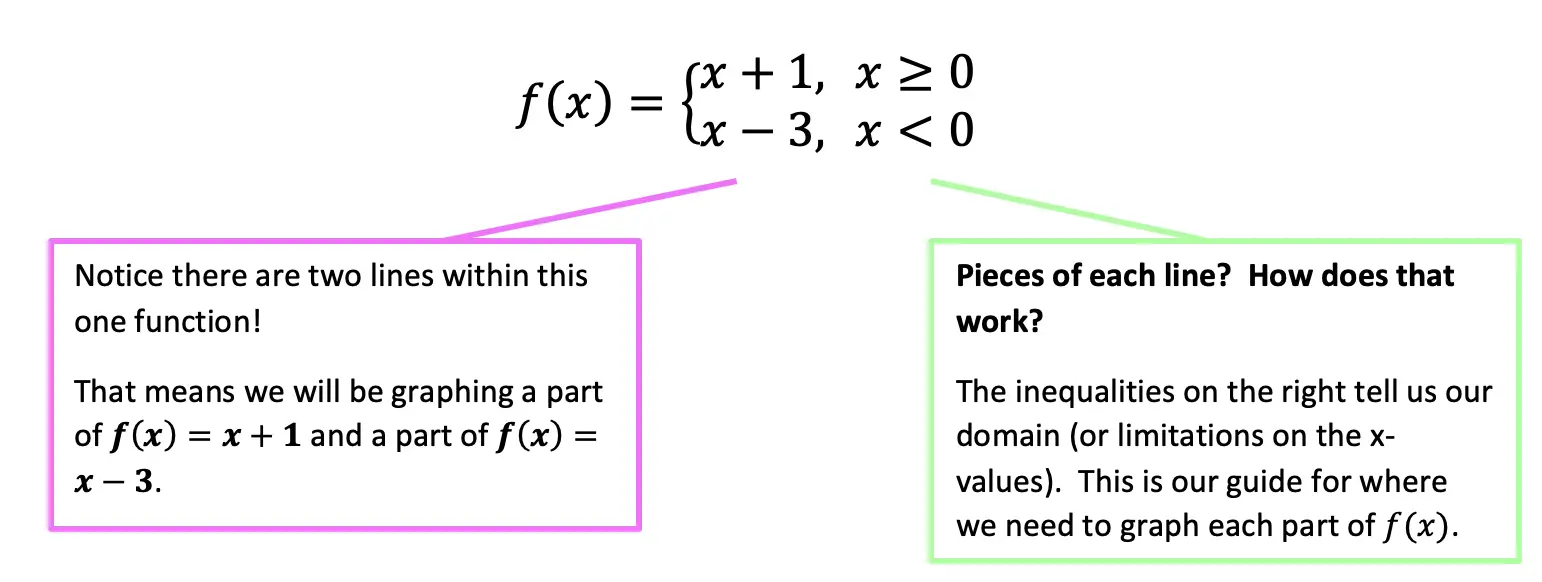
What are Piece-Wise Functions?

Exactly what they sound like! A function that has multiple pieces or parts of a function. Notice our function below has different pieces/parts to it. There are different lines within, each with their own domain.

Now let’s look again at how to solve our example, solving step by step:

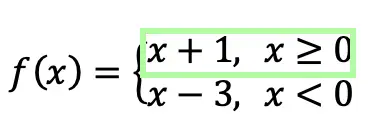
Translation: We are going to graph the line f(x)=x+1 for the domain where x > 0

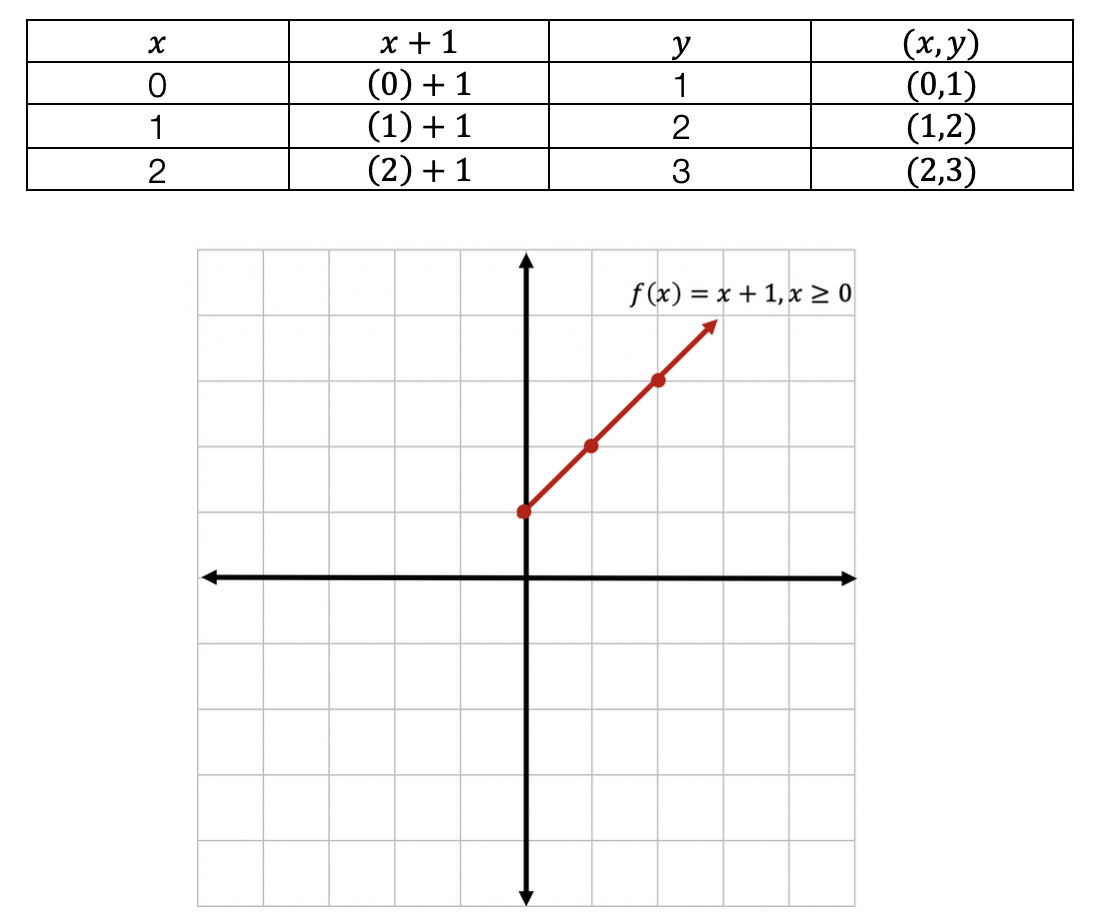
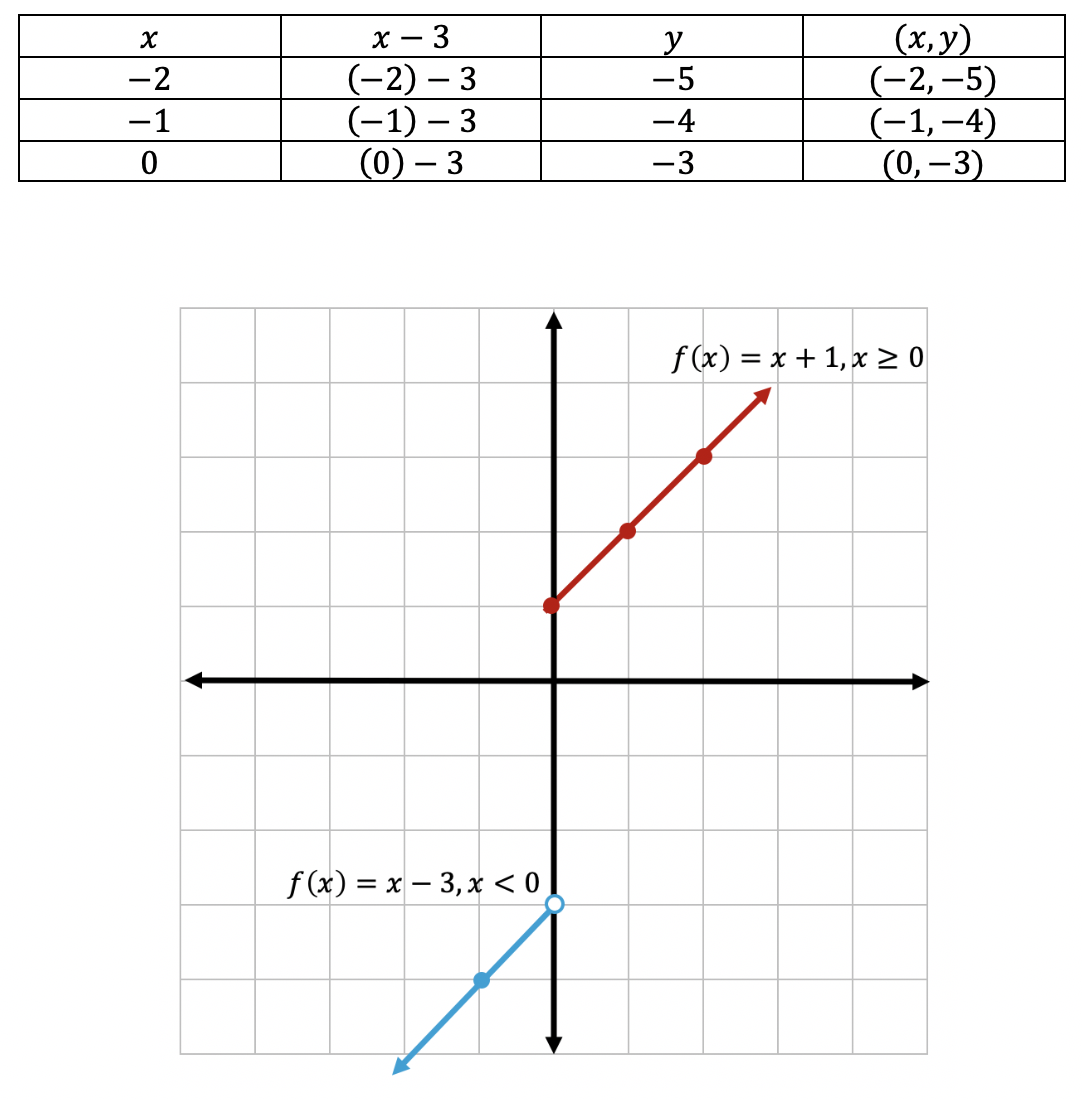
To make sure all our x-values are greater than or equal to zero, we create a table plugging in x-values greater than or equal to zero into the first part of our function, x+1. Then plot the coordinate points x and y on our graph.

Screen Shot 2020-07-21 at 10.05.00 AM.png

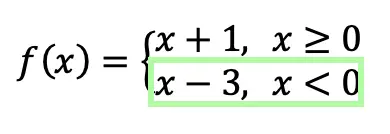
Translation: We are going to graph the line f(x)=x-3 for the domain where x < 0.

To make sure all our x-values are less than zero, let’s create a table plugging in negative x-values values leading up to zero into the second part of our function, x-3. Then plot the coordinate points x and y on our graph.

Ready to try the practice problems below on your own!?

Practice Questions:

Graph each piecewise function:

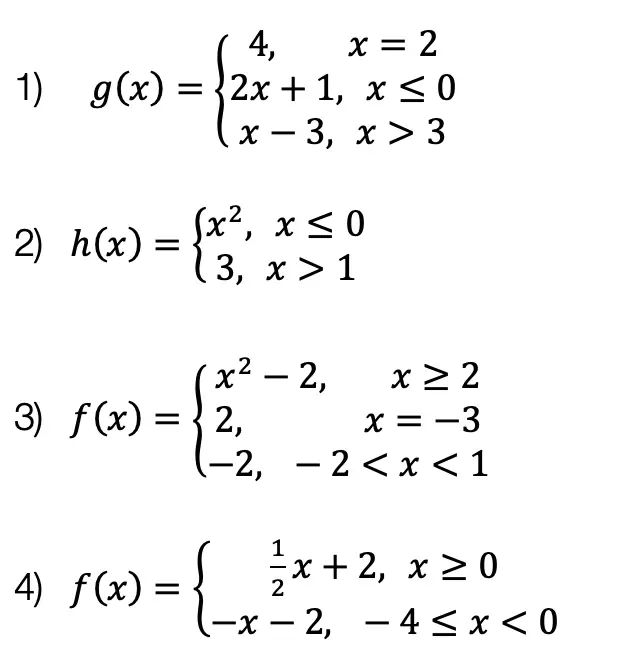
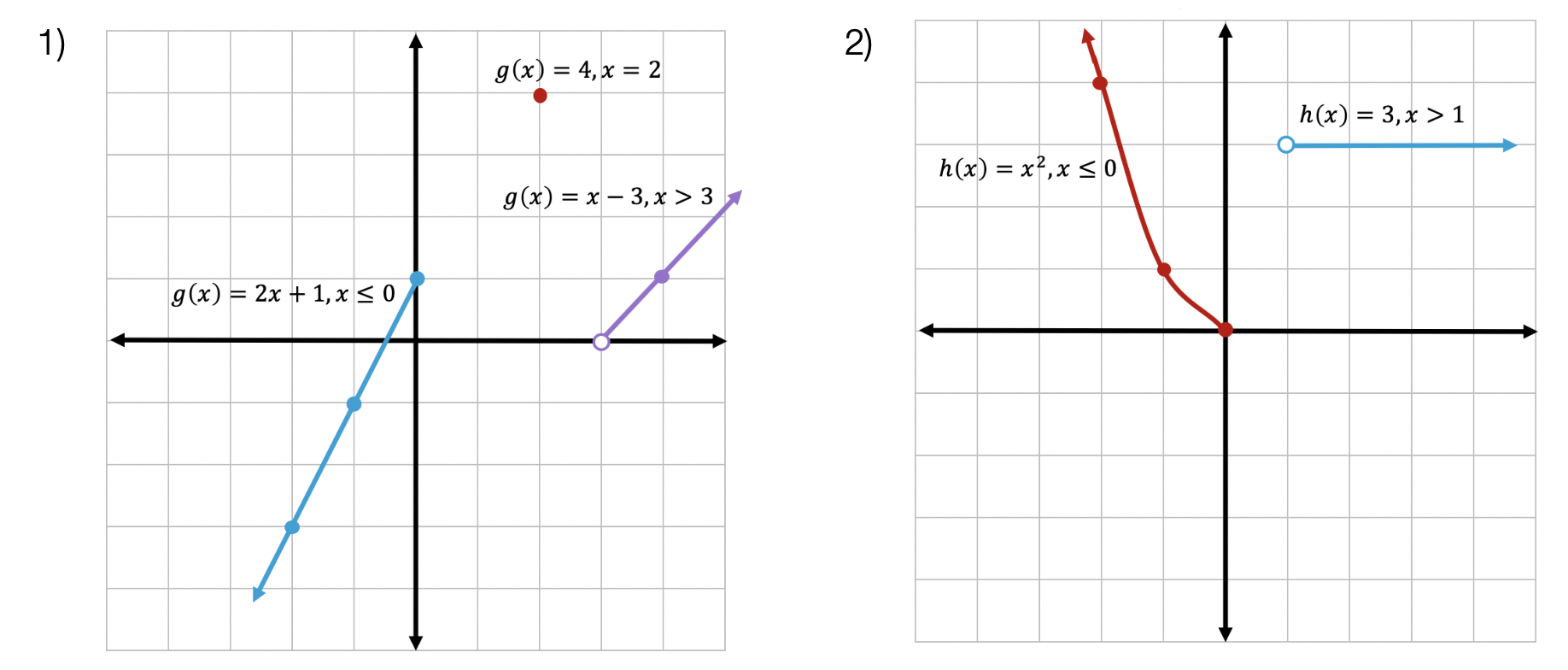
Solutions:

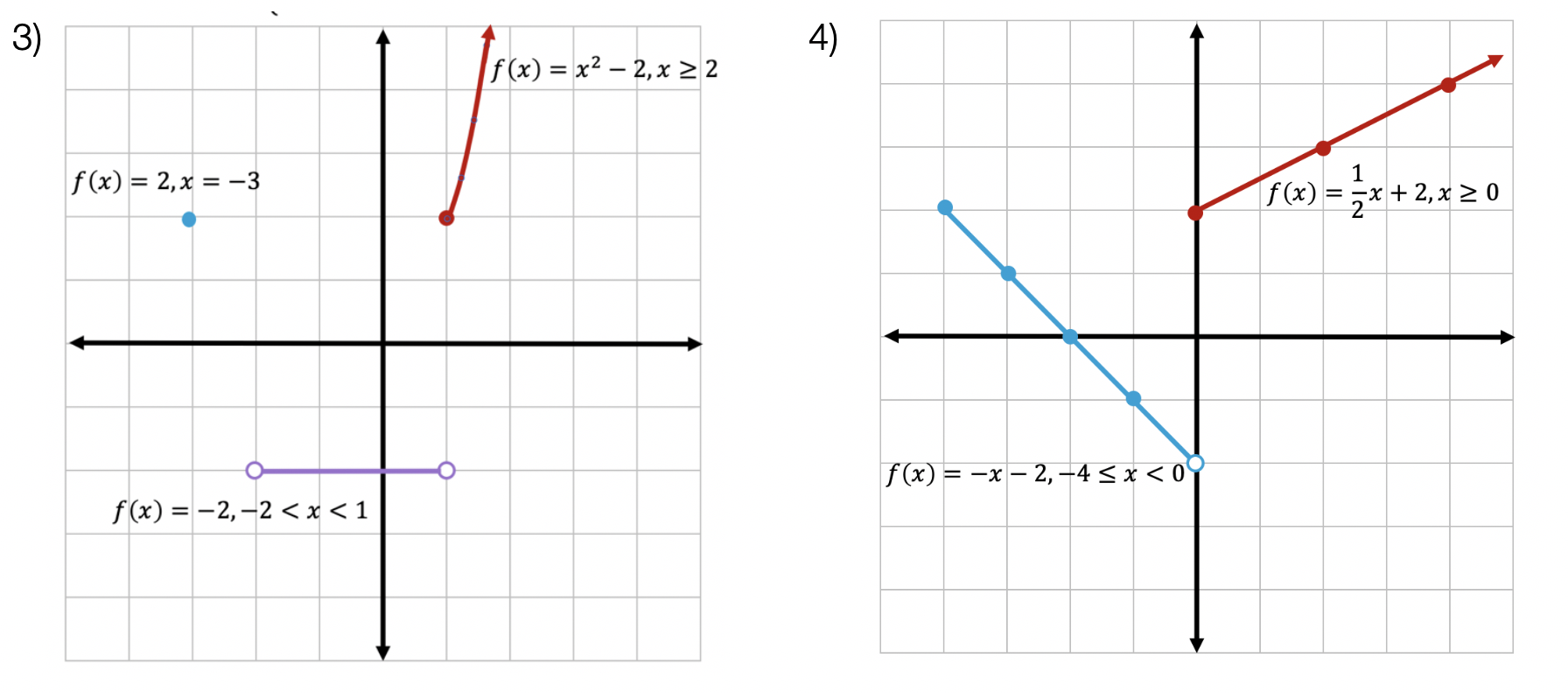
Still got questions? No problem! Check out the video above or comment below for any questions. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

***Bonus! Want to test yourself with a similar NYS Regents question on piecewise functions? Click here.

Intersecting Secants Theorem: Geometry

Ahoy! Today we’re going to cover the Intersecting Secants Theorem! If you forgot what a secant is in the first place, don’t worry because all it is a line that goes through a circle. Not so scary right? I was never scared of lines that go through circles before, no reason to start now.

If you have any questions about anything here, don’t hesitate to comment below and check out my video for more of an explanation. Stay positive math peeps and happy calculating! 🙂

Wait, what are Secants?

Intersecting Secants Theorem: When secants intersect an amazing thing happens! Their line segments are in proportion, meaning we can use something called the Intersecting Secants Theorem to find missing line segments. Check it out below:

Let’s now see how we can apply the intersecting Secants Theorem to find missing length.

Screen Shot 2020-07-14 at 10.45.29 PM.png

Step 1: First, let’s write our formula for Intersecting Secants.

Step 2: Now fill in our formulas with the given values and simplify.

Step 3: All we have to do now is solve for x! I use the product.sum method here, but choose the factoring method that best works for you!

Step 4: Since we have to reject one of our answers, that leaves us with our one and only solution x=2.

Screen Shot 2020-07-14 at 10.14.41 PM.png

Ready to try the practice problems below on your own!?

Practice Questions: Find the value of the missing line segments x.

Solutions:

Screen Shot 2020-07-20 at 9.30.55 AM.png

Still got questions? No problem! Check out the video above or comment below for any questions and follow for the latest MathSux posts. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

To review a similar NYS Regents question check out this post here.

Circle Theorems & Formulas

Central Angle Theorem

Inscribed Angles & Intercepted Arcs

Area of a Sector

Circle Theorems

4 Ways to Factor Trinomials: Algebra

Greeting math peeps and welcome to MathSux! In this post, we are going to go over 4 ways to Factor Trinomials and get the same answer, including, (1) Quadratic Formula (2) Product/Sum, (3) Completing the Square, and (4) Graphing on a Calculator. If you’re looking for more don’t forget to check out the video and practice questions below. Happy Calculating! 🙂

Also, if need a review on Factor by Grouping or Difference of Two Squares (DOTS) check out the hyperlinks here!

*If you haven’t done so, check out the video that goes over this exact problem, and don’t forget to subscribe!

We will take this step by step, showing 4 ways to factor trinomials, getting the same answer each and every time! Let’s get to it!

4 Ways to Factor Trinomials

(1) Quadratic Formula:

____________________________________________________________________

(2) Product/Sum:

4 Ways to Factor Trinomials ____________________________________________________________________

(3) Completing the Square:

4 Ways to Factor Trinomials ____________________________________________________________________

(4) Graph:

Choose the factoring method that works best for you and try the practice problems on your own below!

Practice Questions:

Solutions:

Want a review of all the different factoring methods out there? Check out the ones left out here (DOTS and GCF) and happy calculating! 🙂

For even more ways to factor quadratic equations, check out How to factor by Grouping here! 🙂

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring Review

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Imaginary and Complex Numbers

Quadratic Equations with 2 Imaginary Solutions

Focus and Directrix of a Parabola

Also, if you want more Mathsux? Don’t forget to check out our Youtube channel and more below! If you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Median of a Trapezoid Theorem: Geometry

Hi everyone and welcome to Math Sux! In this post, we are going to look at how to use and applythe median of a trapezoid theorem. Thankfully, it is not a scary formula, and one we can easily master with a dose of algebra. The only hard part remaining, is remembering this thing! Take a look below to see a step by step tutorial on how to use the median of a trapezoid theorem and check out the practice questions at the end of this post to truly master the topic. Happy calculating! 🙂

*If you haven’t done so, check out the video that goes over this exact problem, also please don’t forget to subscribe!

Step 1: Let’s apply the Median of a Trapezoid Theorem to this question! A little rusty? No problem, check out the Theorem below.

Median of a Trapezoid Theorem: The median of a trapezoid is equal to the sum of both bases.Step 2: Now that we found the value of x , we can plug it back into the equation for median, to find the value of median

Want more practice? Your wish is my command! Check out the practice problems below:

Practice Questions:

1.is the median of trapezoid ABCDEF, find the value of the median, given the following:2. is the median of trapezoid ACTIVE, find the value of the median, given the following:3.is the median of trapezoid DRAGON, find the value of the median, given the following:

4. is the median of trapezoid MATRIX, find the value of the median, given the following:

Solutions:

Need more of an explanation? Check out the detailed video and practice problems. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Earth Day Fractals!

In honor of Earth Day last week, I thought we’d take a look at some math that appears magically in nature. Math? In nature? For those of you who think math is unnatural or just terrible in general, this is a great time to be proven otherwise!

The key that links math to nature is all about PATTERNS. All math is based on is patterns. This includes all types of math, from sequences to finding x, each mathematical procedure follows some type of pattern. Meanwhile back in the nearest forest, patterns are occurring everywhere in nature.

The rock star of all patterns would have to be FRACTALS. A Fractal is a repeating pattern that is ongoing and has different sizes of the exact same thing! And the amazing thing is that we can actually find fractals in our ~~neighbor’s~~ local garden.

Let’s look at some Fractal Examples:

(1) Romanesco Broccoli: Check out those repeating shapes, that have the same repeating shapes on those shapes and the same repeating shapes on even smaller shapes and…. my brain hurts!

(2) Fern Leaves: The largest part of this fractal is the entire fern leaf itself. The next smaller and identical part is each individual “leaf” along the stem. If you look closely, the pattern continues!

(3) Leaves: If you’ve ever gotten up real close to any type of leaf, you may have noticed the forever repeating pattern that gets smaller and smaller. Behold the power and fractal pattern of this mighty leaf below!

.

Just in case fractals are still a bit hard to grasp, check out the most famous Fractal below, otherwise known as Sierpinski’s Triangle. This example might not be found in your local back yard, but it’s the best way to see what a fractal truly is up close and infinite and stuff.

Looking for more math in nature? Check out this post on the Golden Ratio and happy calculating! 🙂

| Facebook | Twitter |