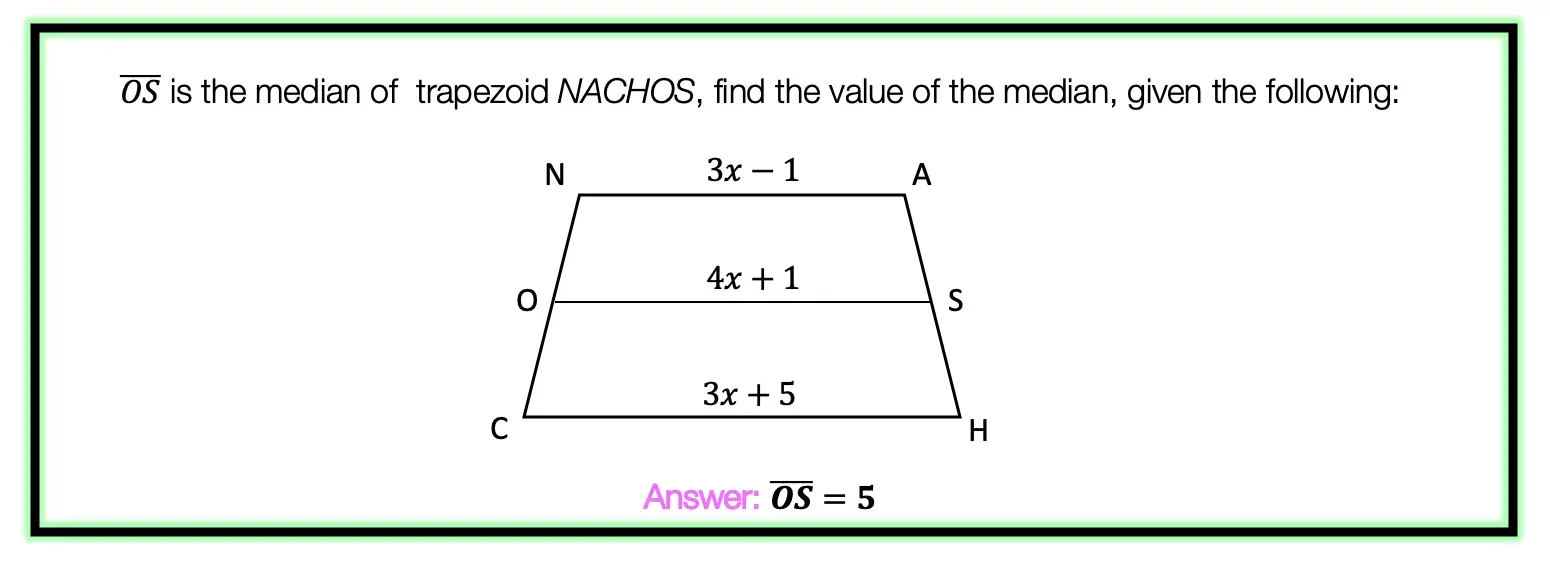
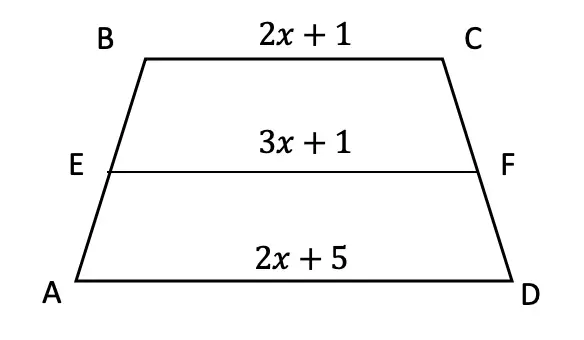
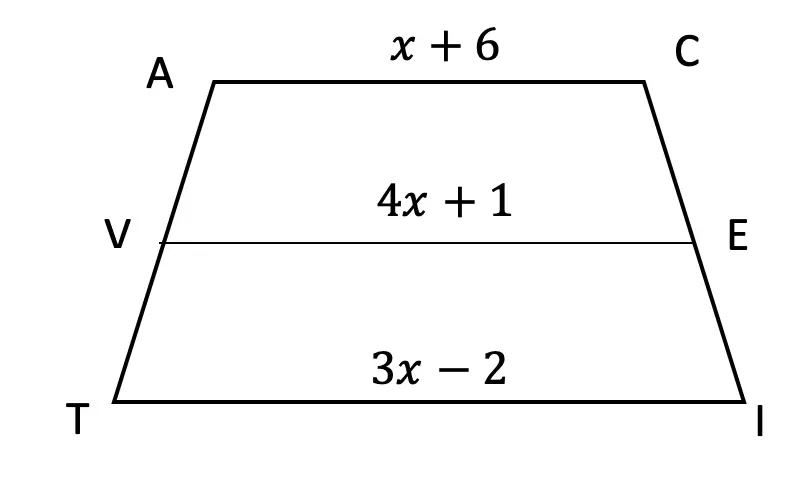
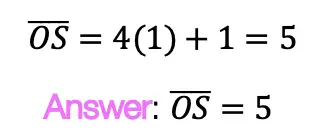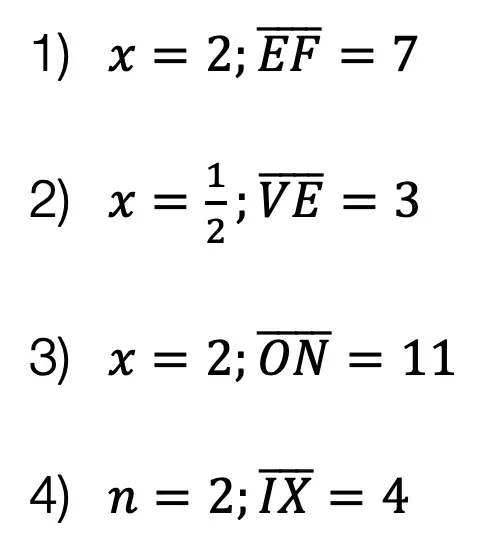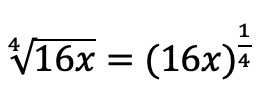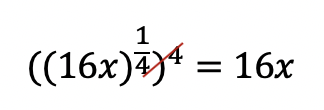Greetings and welcome to Mathsux! Today we are going to go over reflections geometry, one of the many types of transformations that come up in geometry. And thankfully, reflection transformation is one of the easiest types to master, especially if you’re more of a visual learner/artistic type person. In this post, we will go over a reflection across the line x=-2, but if you want to see a reflection across the x axis, the y axis, and the line y=x, please check out the math video below! So let’s get to it! And if you’re new to transformations, check out translations here.
What are Reflections?
A Reflection on a coordinate plane is exactly what you think! A reflection is a type of transformation in geometry where we reflect a point, a line segment, or a shape over a line to create a mirror image of itself. Think of the wings of a butterfly, a page being folded in half, or anywhere else where there is perfect symmetry, each of these are great examples of a reflection!
Reflection Rules:
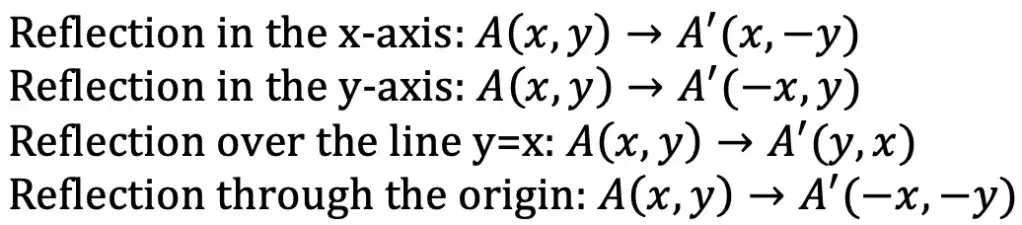
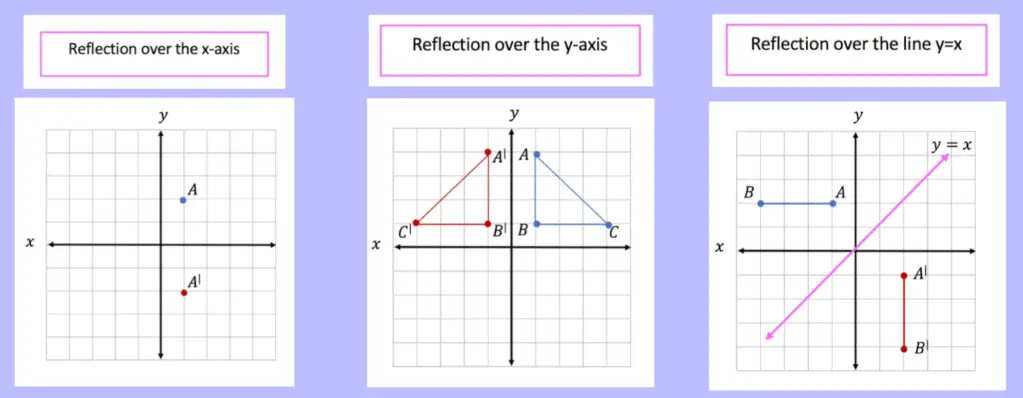
If you are completely new to reflections, you may want to check out the video above that goes into deriving reflection rules over the different axis. But for those of you more comfortable with reflection, check out the example below where we reflect the image of a triangle onto itself over the line x=-2.
Example:
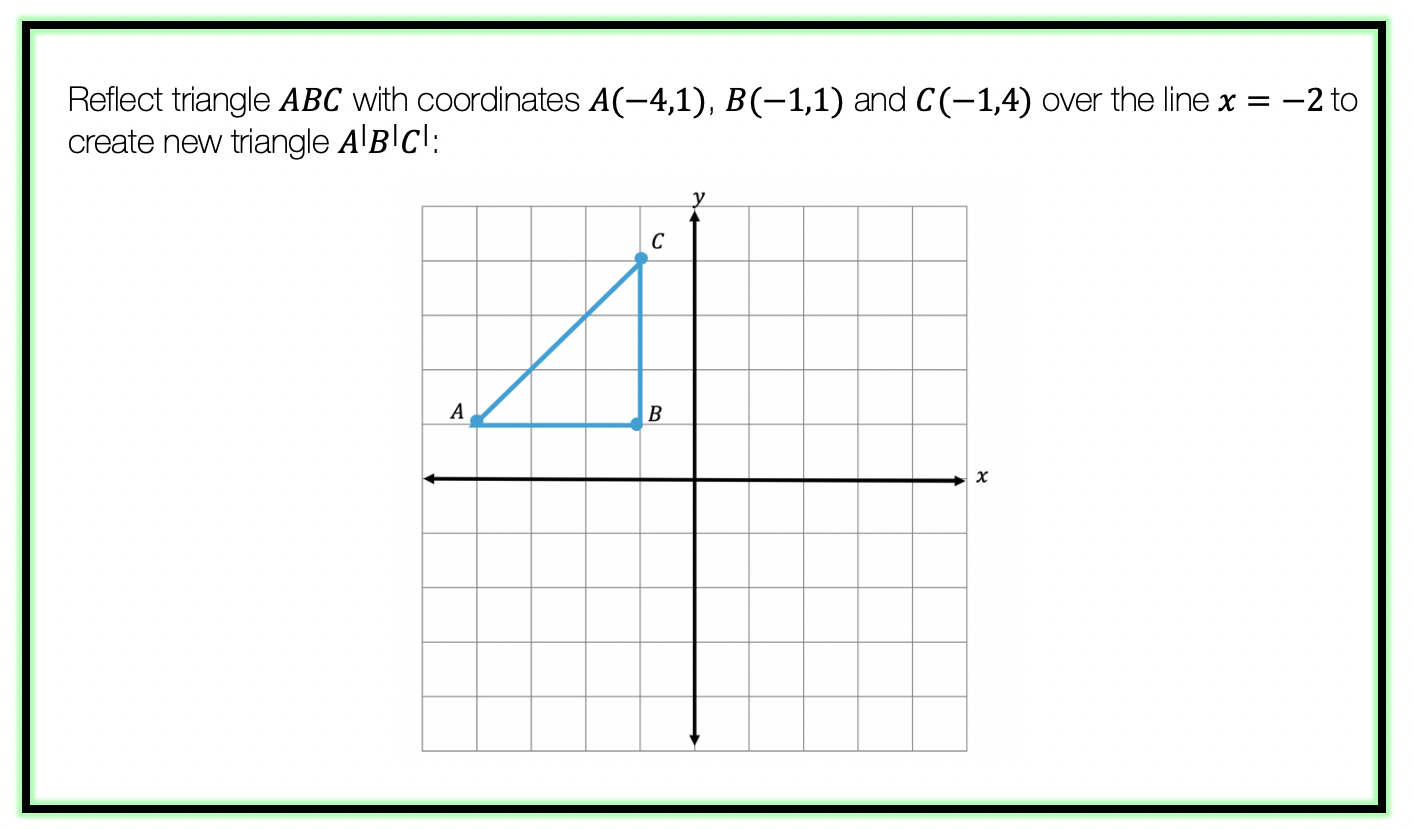
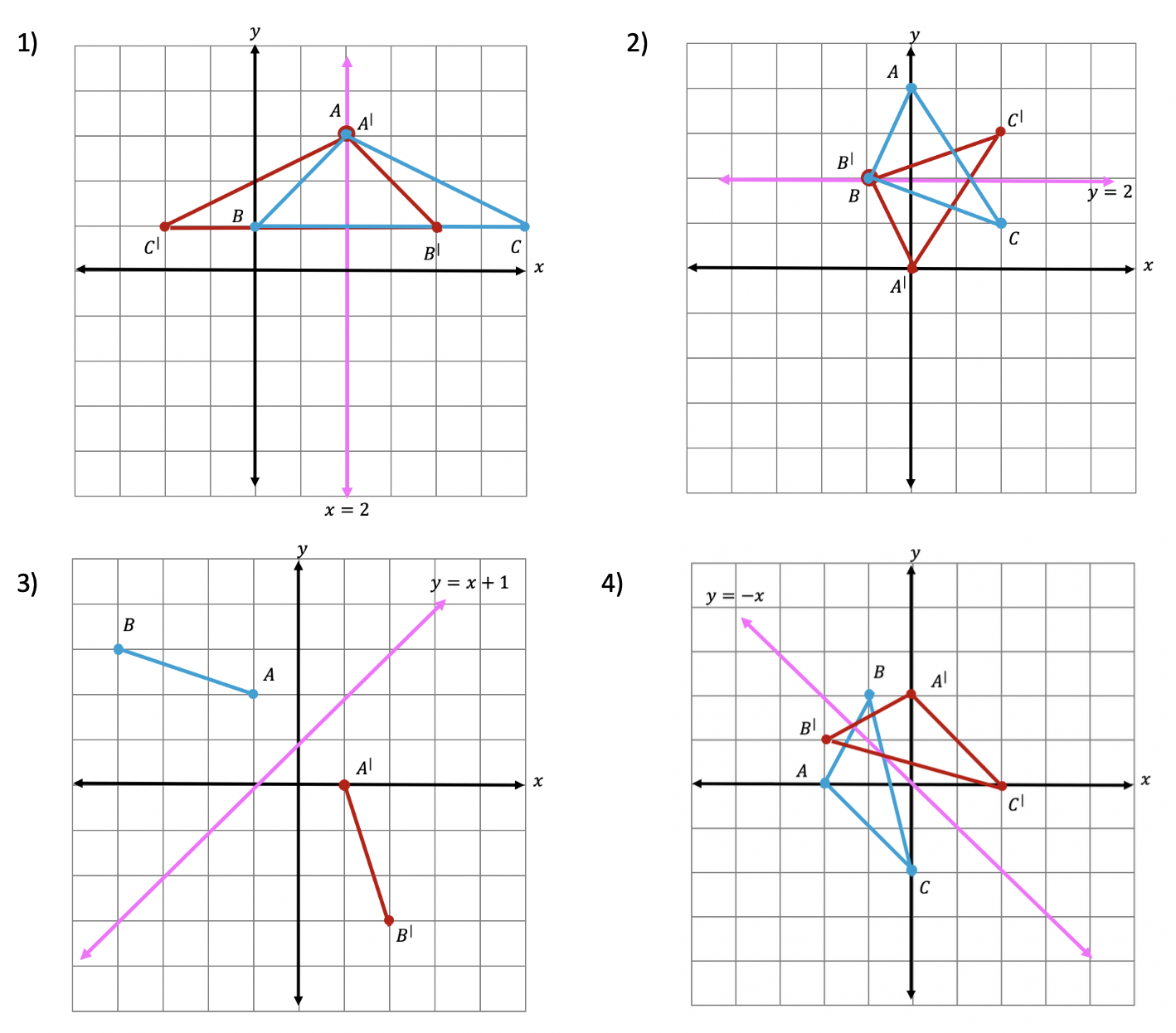
Step 1: First, let’s draw in line x=-2. Note that whenever we have x equal to a number, we end up drawing a vertical line at that point on the x axis, in this case at x=-2.
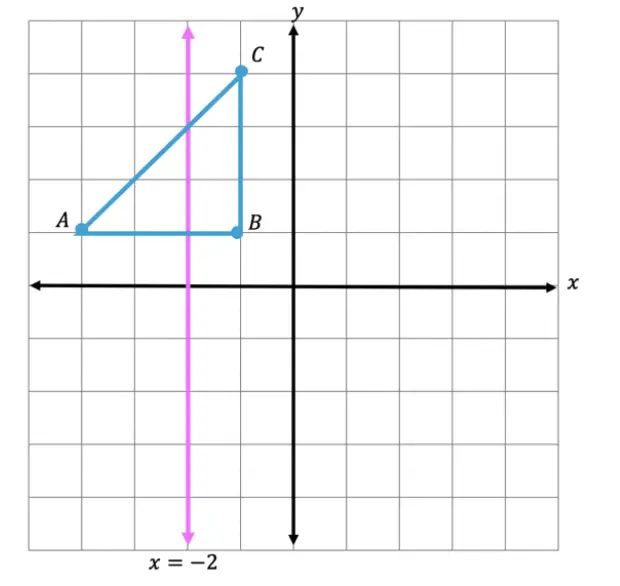
Step 2: Find the distance each point is from the line x=-2 and reflect it on the other side, measuring the same distance.
First, let’s look at point C, notice it’s 1 unit away from the line x=-2 on the right. To reflect point c, we are going to count 1 unit but this time to the left of the line x=-2 and label our new point, C|.
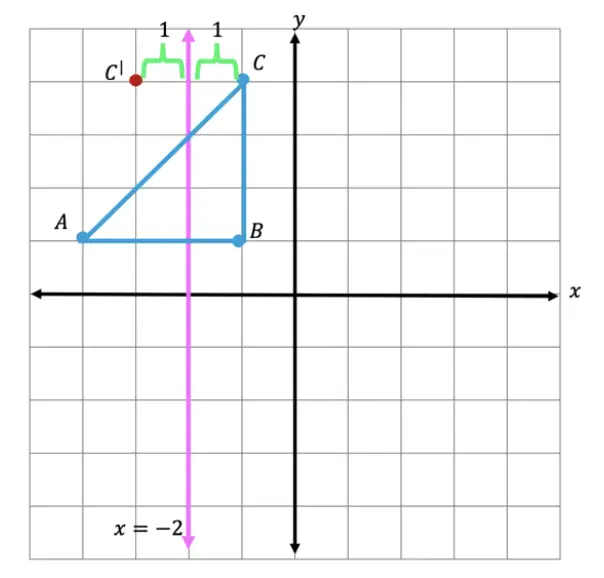
Step 3: Now we are going to reflect coordinate point A in much the same way! Notice that point A is 2 units away on the left of line x=-2, we then want to measure 2 units to the right of our line x=-2 and mark our new coordinate point, A|.
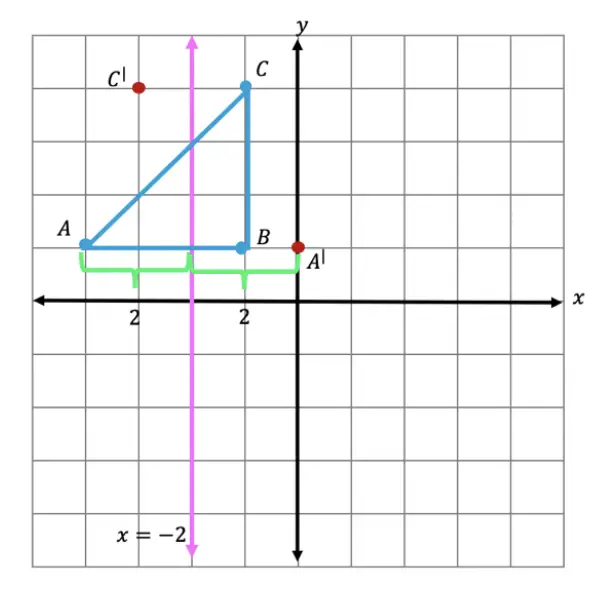
Step 4: Lastly, we want to reflect coordinate point B. This time, point B is 1 unit away on the right side of the line x=-2, we then measure 1 unit to the opposite direction of our line, x=-2, and mark our new point, B|.
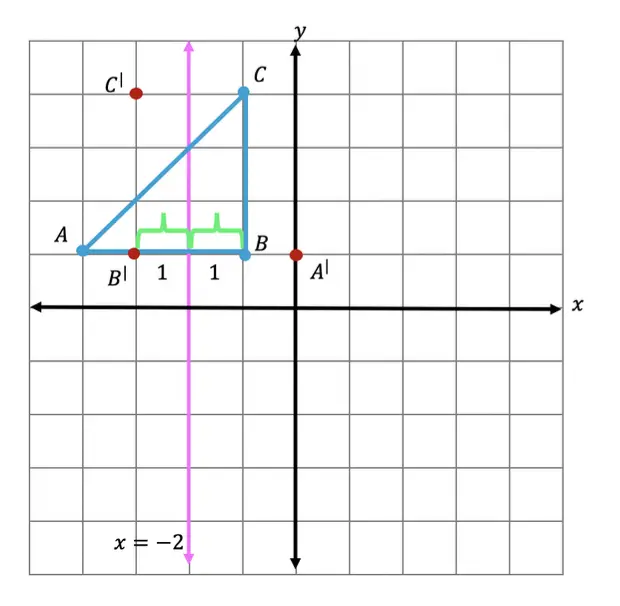
Step 5: Now that we have all the newly reflected coordinate points of our triangle, finally, we can now connect them all, for our fully reflected image of right triangle A|B|C|.
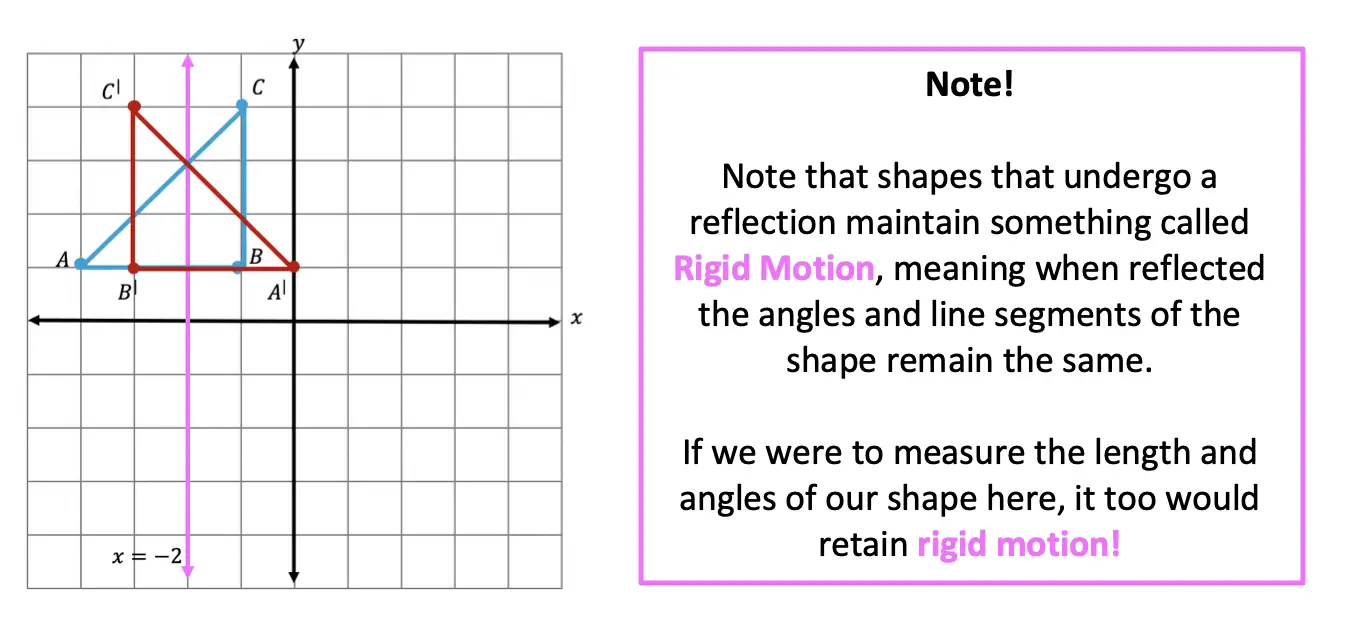
Notice our newly reflected triangle is not just a mirror image of itself, but when the original figure is reflected it actually ends up overlapping onto itself!? How did this happen? That is because this our reflection line came right down the middle of our original image, triangle ABC. Shapes that reflect onto themselves are a bit tricky but not impossible, just remember to measure out the distance of each coordinate point and reflections should be a breeze!
Rigid Motion:
Reflections are a special type of transformation in geometry that maintains rigid motion, meaning when a point, line, or shape is reflected the angles, and line segments retain their value. For example, if we were to measure the area of both right triangles, before and after reflection, we would find the areas to remain unchanged. Meaning the area of triangle ABC is equal to the area of triangle A|B|C| . Another rigid transformation includes rotations and translations.
Looking to practice your new reflection skills? Try the reflection practice problems below, with solutions to each question, to truly master the topic! Happy calculating!
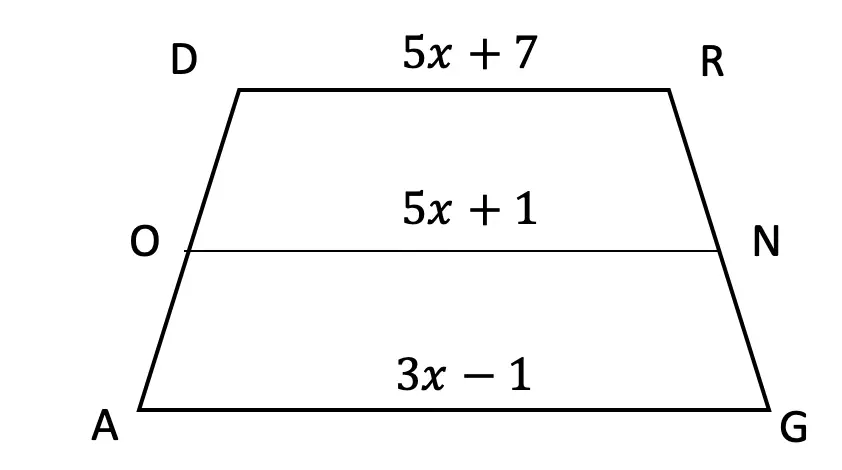
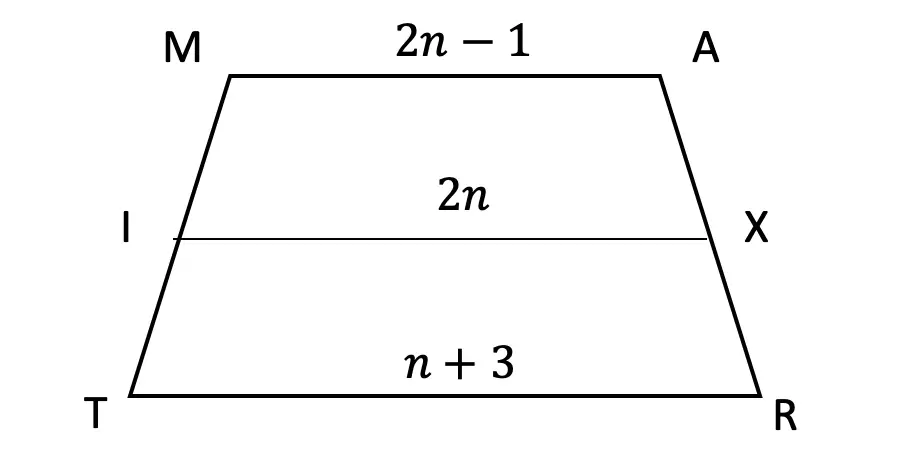
Practice Questions:
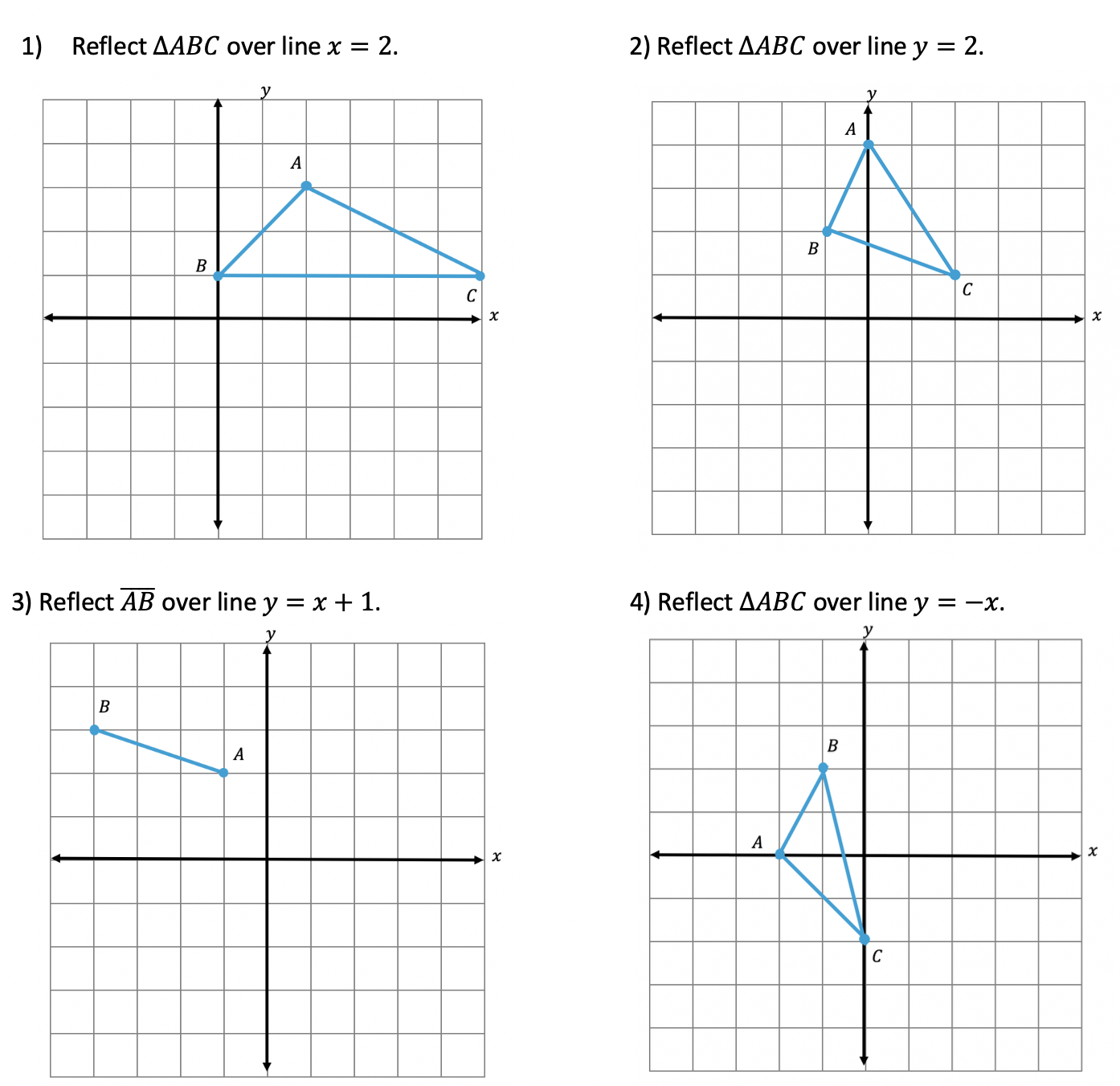
Solutions:
Still got questions? No problem! Check out the video above or comment below! There is also a bonus video if you scroll all the way down at the end of this post for anyone who wants to see how to reflect a line over the line x=2. See how it differs and how it is similar to the example shown here. Happy calculating! 🙂
Don’t forget to follow MathSux on social media for the latest tips and tricks to ace math!
Facebook ~ Twitter ~ TikTok ~ Youtube
And if you are looking for more Transformations Check out the related posts below and let me know if you have any questions? Or maybe you just want to share your favorite type of transformation? Either way, happy calculating!
median, to find the value of median 
is the median of trapezoid ABCDEF, find the value of the median, given the following:2. 
is the median of trapezoid ACTIVE, find the value of the median, given the following:3.
is the median of trapezoid DRAGON, find the value of the median, given the following:
is the median of trapezoid MATRIX, find the value of the median, given the following:
