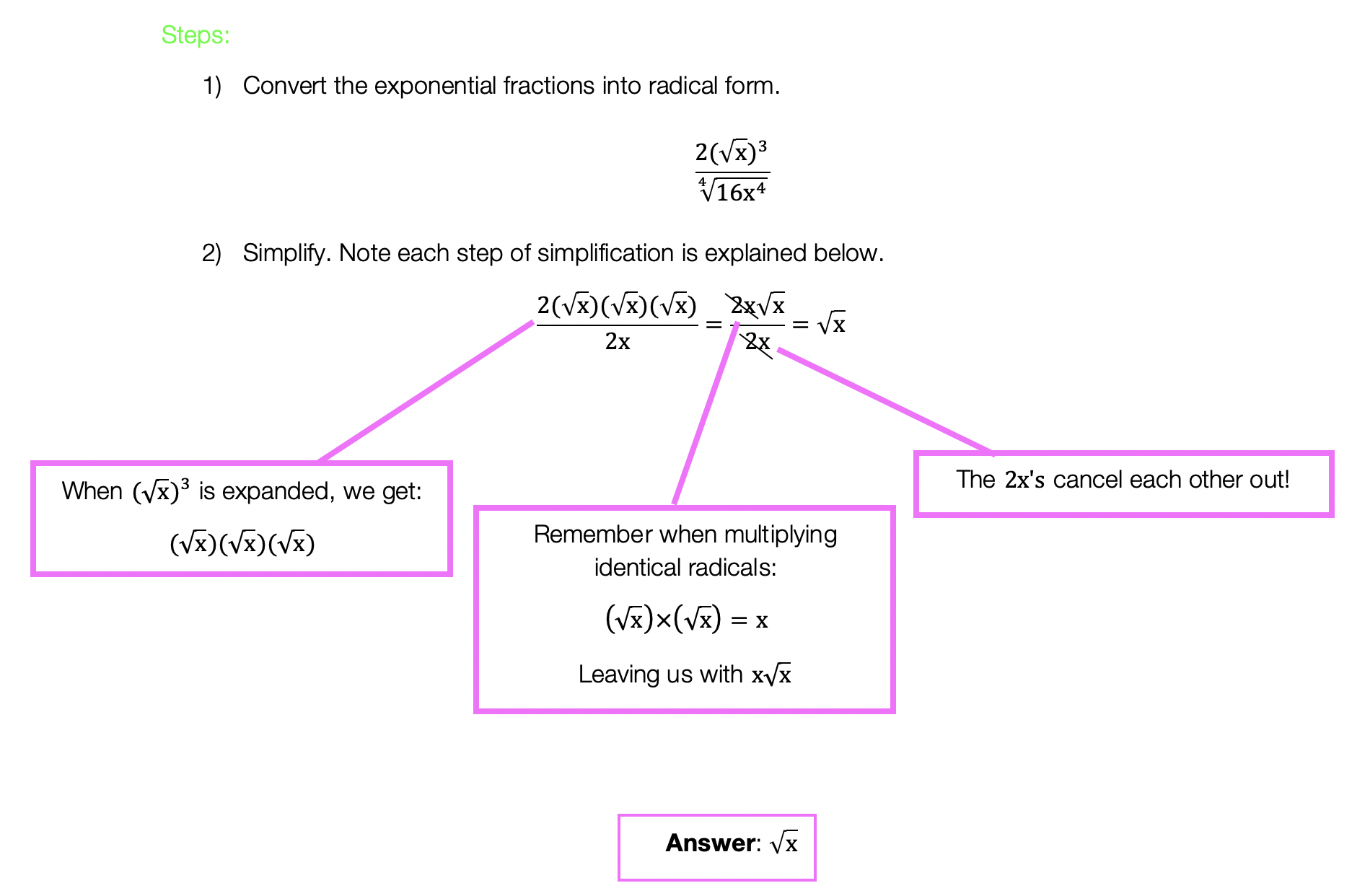
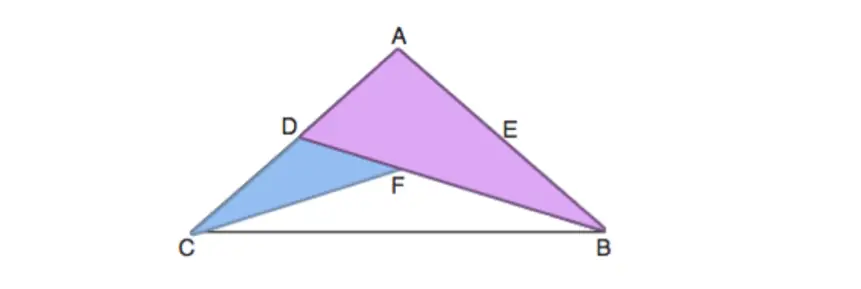
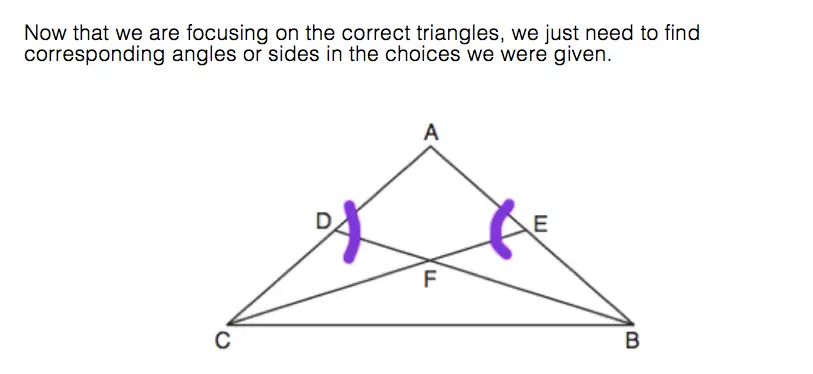
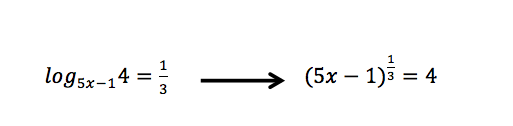
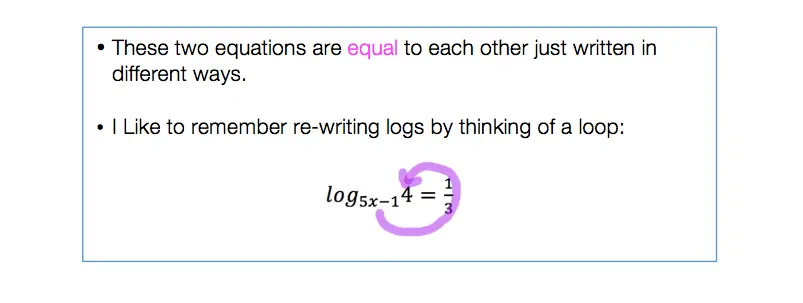
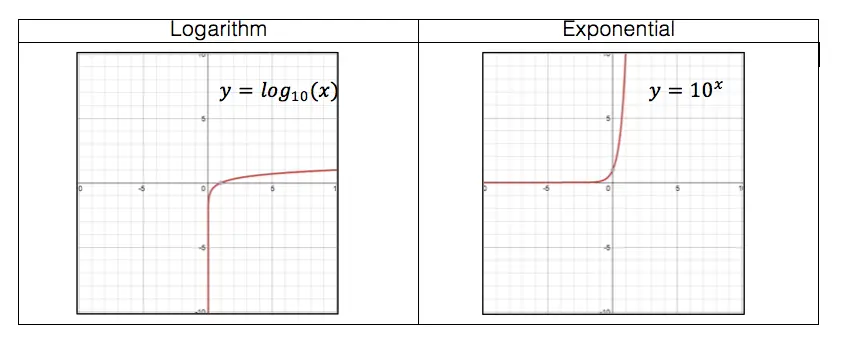
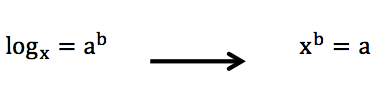
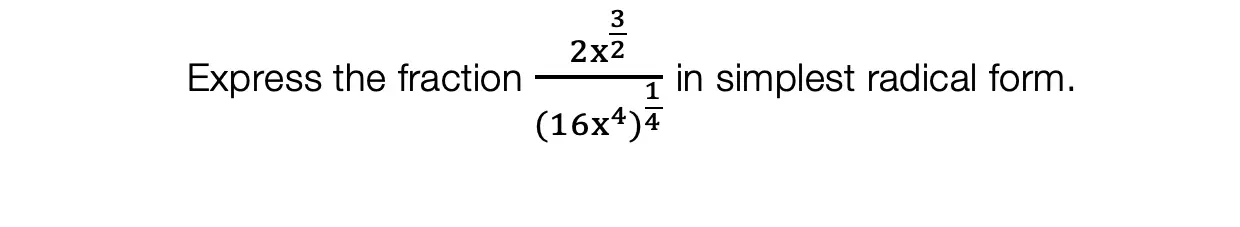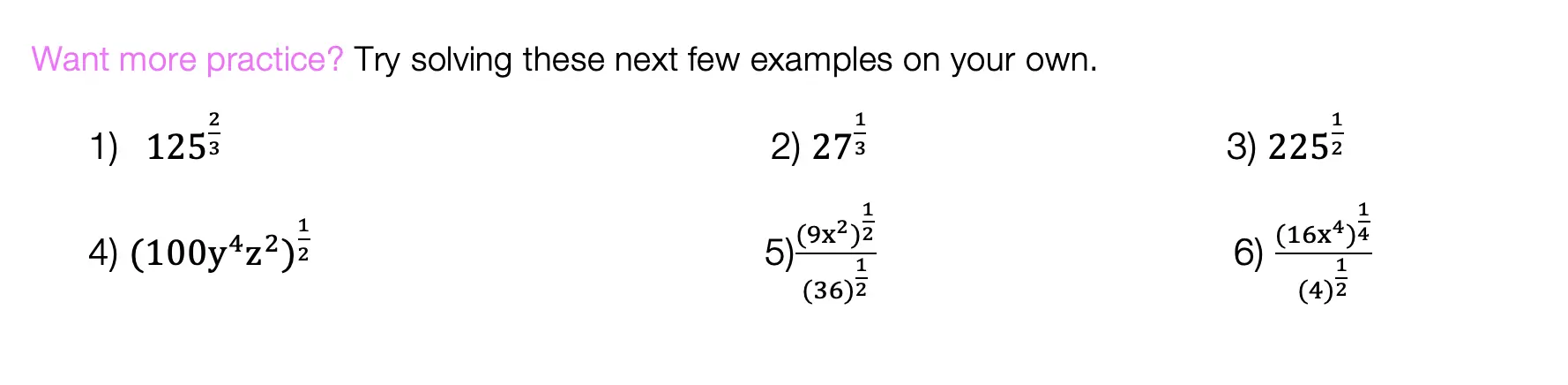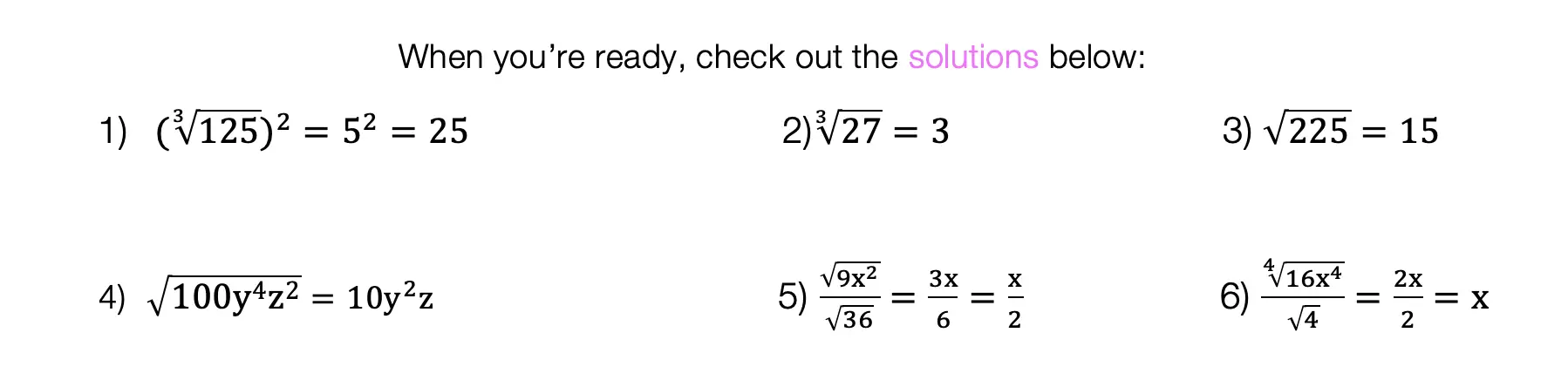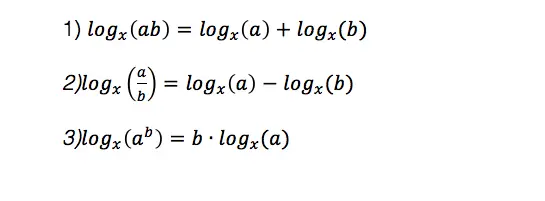Study Archives - Page 3 of 3

Math Resources (in the time of COVID)

Calling all students, teachers, and parents! As everyone is stuck at home during a global pandemic, now is a ~~great~~ time we are all forced to try and understand math (and our sanity level) a little bit more. Well, I may not be able to help you with the keeping sanity stuff, but as far as math goes, hopefully, the below math resources offer some much needed mathematic support.

All jokes aside I hope everyone is staying safe and successfully social distancing. Stay well, math friends! 🙂

Kahn Academy: The same Kahn Academy we know and love still has amazing videos and tutorials as usual, but now they also have a live “homeroom” chat on Facebook LIVE every day at 12:00pm. The chats occur daily with Kahn Academy founder Sal and at times feature famous guests such as Bill Gates. Click the link below for more:

Khan Academy Homeroom

Study.com: In a time when companies are being more generous, Study.com is here for us as they offer up to 1000 licenses for school districts and free lessons for teachers, students, and parents. Check out all the education freebies here:

Study.com

Math Planet: If you’re looking for free math resources in Pre-Algebra, Algebra, Algebra 2, and Geometry then you will find the answers you need at Math Planet. All free all the time, find their website here:

MathPlanet

MathSux: Clearly, I had to mention MathSux, the very site you are on right now! Check out free math videos, lesson, practice questions, and more for understanding math any way that works for you!

MathSux

What is your favorite educational site? Let me know in the comments, and stay well! 🙂

Binomial Cubic Expansion: Algebra 2/Trig.

Hey math friends! In this post, we are going to go over Binomial Cubic Expansion by going step by step! We’ll start by reviewing an old Regents question. Then, to truly master the topic, try the practice problems at the end of this post on your own! And, if you still have questions, don’t hesitate to watch the video or comment below. Thanks for stopping by and happy calculating! 🙂

Also, if you’re looking for more on Binomial Cubic Expansion, check out this post here!

What are Cubed Binomials?

Binomials are two-termed expressions, and now we are cubing them with a triple exponent! See how to tackle these types of problems with the example below:

How do I answer this question?

We need to do an algebraic proof to see if (a+b)³=a³+b³.

How do we do this?

We set each expression equal to one another, and try to get one side to look like the other by using FOIL and distributing. In this case, we will be expanding (a+b)³ to equal (a+b)(a+b)(a+b).

Extra Tip! Notice that we used something called FOIL to combine (a+b)(a+b). But what does that even mean? FOIL is an acronym for multiplying the two terms together. It’s a way to remember to distribute each term to one another. Take a look below:

Screen Shot 2019-05-24 at 9.02.50 AM.png

Screen Shot 2019-05-24 at 9.03.23 AM.png

Add and combine all like terms together and we get !

_______________________________________________________________________

Keep in touch with MathSux and get FREE math videos, lessons, and practice questions straight to your inbox! Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Intersecting Secants: Geometry

intersecting secants theorem

Hey math friends! In today’s post, we are going to go over the Intersecting Secants Theorem, specifically using it to find the piece of a missing length on a secant line. We are also going to see proof as to why this theorem works in the first place!

Just a warning: this blog post contains circles. This usually non-threatening shape can get intimidating when secants, chords, and tangents are involved. Luckily, this question is not too complicated and was also spotted on the NYS Regents. Before looking at the questions below, here is a review on different parts of a circle. Pay close attention to what a secant is, which is what we’ll be focusing on today:

Think you are ready? Let’s look at that next question!

What information do we already have? Based on the question we know:

Screen Shot 2018-12-25 at 12.54.24 PM.png

*Extra Tip! Why does this formula work in the first place!?? If we draw lines creating and proving triangle RTQ and triangle RPS are similar by AA, this leads us to know that the two triangles have proportionate sides and can follow our formula! ___________________________________________________________________________________

Still got questions? Let me know in the comments and remember having questions is a good thing!

If you’re looking for more on intersecting secants, check out this post here for practice questions and more!

Facebook ~ Twitter ~ TikTok ~ Youtube

Rational Exponents: Algebra 2/Trig.

Hi everyone and welcome to MathSux! In this post we are going to break down and solve rational exponents. The words may sound like a mouthful, but all rational exponents are, are fractions as exponents. So instead of having x raised to the second power, such as x², we might have x raised to the one-half power, such as x^(1/2). Let’s try an example taken straight from the NYS Regents below. Also, if you have any questions don’t hesitate to comment below or check out the video posted here. Happy calculating! 🙂

How do I answer this question?

The questions want us to simplify the rational exponents into something we can understand.

How do we do this?

We are going to convert the insane looking rational exponents into radical and solve/see if we can simplify further.

Reminder!

A radical can be converted into a rational exponent and vice versa. Not sure what that means? It’s ok! Take a gander at the examples below and look for a pattern:

Think you’re ready to take on our original problem? #Letsdothis

Example:

Screen Shot 2018-12-16 at 2.21.06 PM.png

Practice:

Solutions:

Screen Shot 2018-12-16 at 2.20.42 PM.png

Still got questions? Don’t hesitate to comment below for anything that still isn’t clear! Looking to review how to solve radical equations? Check out this post here! 🙂

Also, don’t forget to follow MathSux fopr FREE math videos, lessons, practice questions and more every week!

Facebook ~ Twitter ~ TikTok ~ Youtube

How to Factor Quadratic Equations: Algebra

In this post, we are going to dive deep into how to factor Quadratic equations! There are so many different methods to choose from including GCF, Product/Sum, DOTS, and the Quadratic Formula. Here we will go step by step into each method on how to factor quadratic equations, each with their own set of practice questions. For a review on how to factor by grouping, check out this post here and happy calculating! 🙂

Why factor in the first place, you may say? We want to manipulate the equation until we solve for x. Solving for x is our main goal, and factoring allows us to do that. Now let’s get to the good stuff!

How to factor quadratic equations

Greatest Common Factor (GCF):

The greatest common factor is the highest possible number that can be divided out from an equation. This gets the equation into its simplest form and makes it easier for us to solve for x.

Before considering which type of factoring methdo to use, always ask yourself, “Can I take out a GCF?”

How to factor quadratic equations

Product/Sum:

This factoring method is for quadratic equations only! That means the equation takes on the following form:

How to factor quadratic equations

Difference of Two Squares DOTS)

Not to play favorites or anything, but DOTS is the easiest and most lovable of the factoring methods. This factoring method just makes you feel all warm and fuzzy inside or maybe that’s just me). Before we get into how to do DOTS, let’s talk about when?

Quadratic Formula:

We have heard of the quadratic equations, so how id the quadratic formula different?

The Answer: The Quadratic Formula is what we use to factor any trinomial. You can use product/sum on trinomials like we discussed earlier, but this may not always work out easy. The Quadratic Formila on the other hand will work every time!

Low and behold, the Quadratic Formula:

Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Quadratic Equations with 2 Imaginary Solutions

Imaginary and Complex Numbers

Focus and Directrix of a Parabola

Facebook ~ Twitter ~ TikTok ~ Youtube

Why Must We Complete the Square?: Algebra

Completing the Square: So many steps, such little time. It sounds like it involves a square or maybe this is a geometry problem? Why am I doing this again? Why must we complete the square in the first place?

These are all the thoughts that cross our minds when first learning how to complete the square. Well, I’m here to tell you there is a reason for all those steps and they aren’t that bad if you really break them down, let’s take a look!

Answer: x={-7,3}

Explanation:

I’m not going to lie to you here, there are a lot of seemingly meaningless steps to completing the square. The truth is though (as shocking as it may be), is that they are not meaningless, they do form a pattern, and that there is a reason! Before we dive into why let’s look at how to solve this step by step:

Feeling accomplished yet!? Confused? All normal feelings. There are many steps to this process so go back and review, practice, and pay close attention to where things get fuzzy.

But the big question is why are we doing these steps in the first place? Why does this work out, to begin with?

For those of you who are curious, continue to read below!

Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating!

Need more of an explanation? Check out why we complete the square in the first place here !

Facebook ~ Twitter ~ TikTok ~ Youtube

Geometry: Congruent Triangles

Screen Shot 2017-07-27 at 10.07.39 AM

screen-shot-2016-09-12-at-3-47-06-pm

screen-shot-2016-09-12-at-3-48-09-pm

screen-shot-2016-09-12-at-3-49-17-pm

Not bad, eh? If there is anything you have questions on please don’t hesitate to ask! 🙂 If you are looking to test out your skills on this topic even more, check out more challenging questions here.

And for more of me and my nerdy math jokes take a look at MathSux on

Twitter and Facebook. Happy calculating! 🙂

Solving Log Equations: Algebra 2/Trig.

Ahoy math friends! In this post, we are going to focus on solving log equations by solving this Regents questions step by step. We’ll answer this question right away! But if you need more of a review, keep reading and you will find what logarithms are, the different kinds of logarithms rules, and some simpler examples. Ready for our first example?! Check it out below:

How do I Answer this Question?

Step 1: Let’s re-write the equation to get rid of the “log.”

Step 2: Solve for x in our new equation (5x-1)^(1/3)=4

If the above answer makes sense to you, great! If not, that’s ok too, keep reading for a review on solving log equations.

What are Logarithms?

Logarithms are inverses of exponential equations. Take a look below for a clearer picture.

Basic Formula:

Logarithms can be re-written to get rid of the word “log.” This makes them easier to solve and understand.

Log Rules:

There are a few rules you have to ~~memorize~~ get used to with practice. These rules are used when solving for x in different kinds of algebraic log problems:

Still got questions? No problem! Check out the videos below and the post here for more on logarithms! Also don’t forget to subscribe below to get the latest FREE math videos, lessons, and practice questions from MathSux. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for another math challenge? Check out this post on solving 3 simultaneous equations at once!