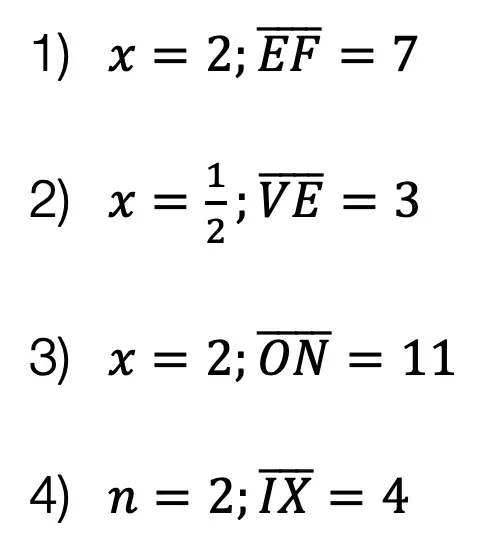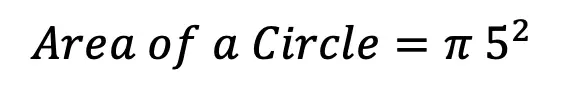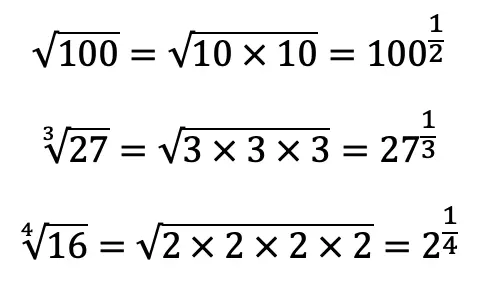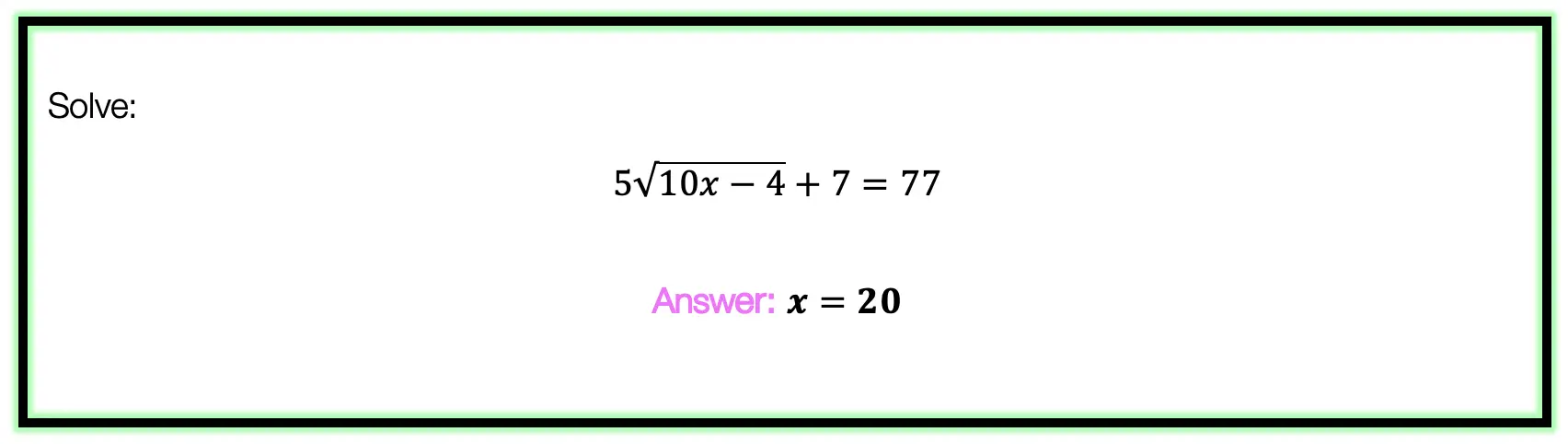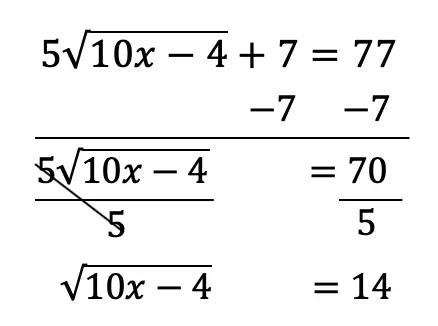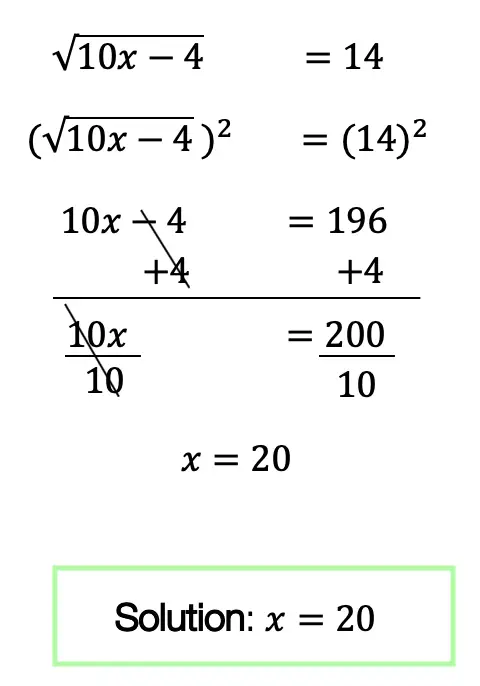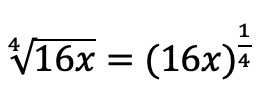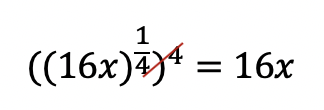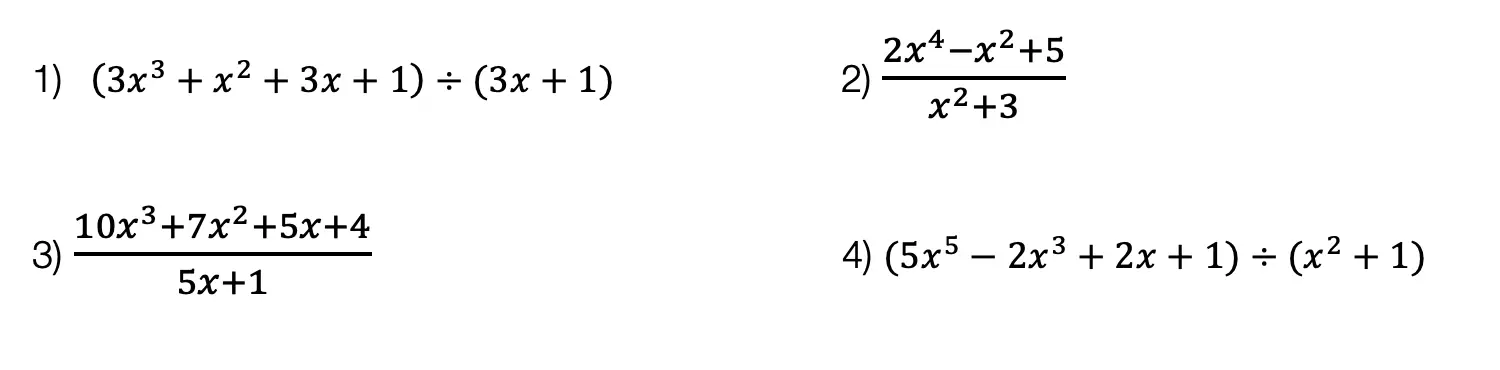Study Archives - Page 2 of 3

How to Solve Log Equations: Algebra 2/Trig.

Welcome to Mathsux! Today, we’re going to go over how to solve log equations, yay! But before we get into finding x, though, we need to go over what log equations are and why we use them in the first place…..just in case you were curious!

Also, if you have any questions about anything here, don’t hesitate to comment below or shoot me an email. Happy calculating! 🙂

What are Log Equations?

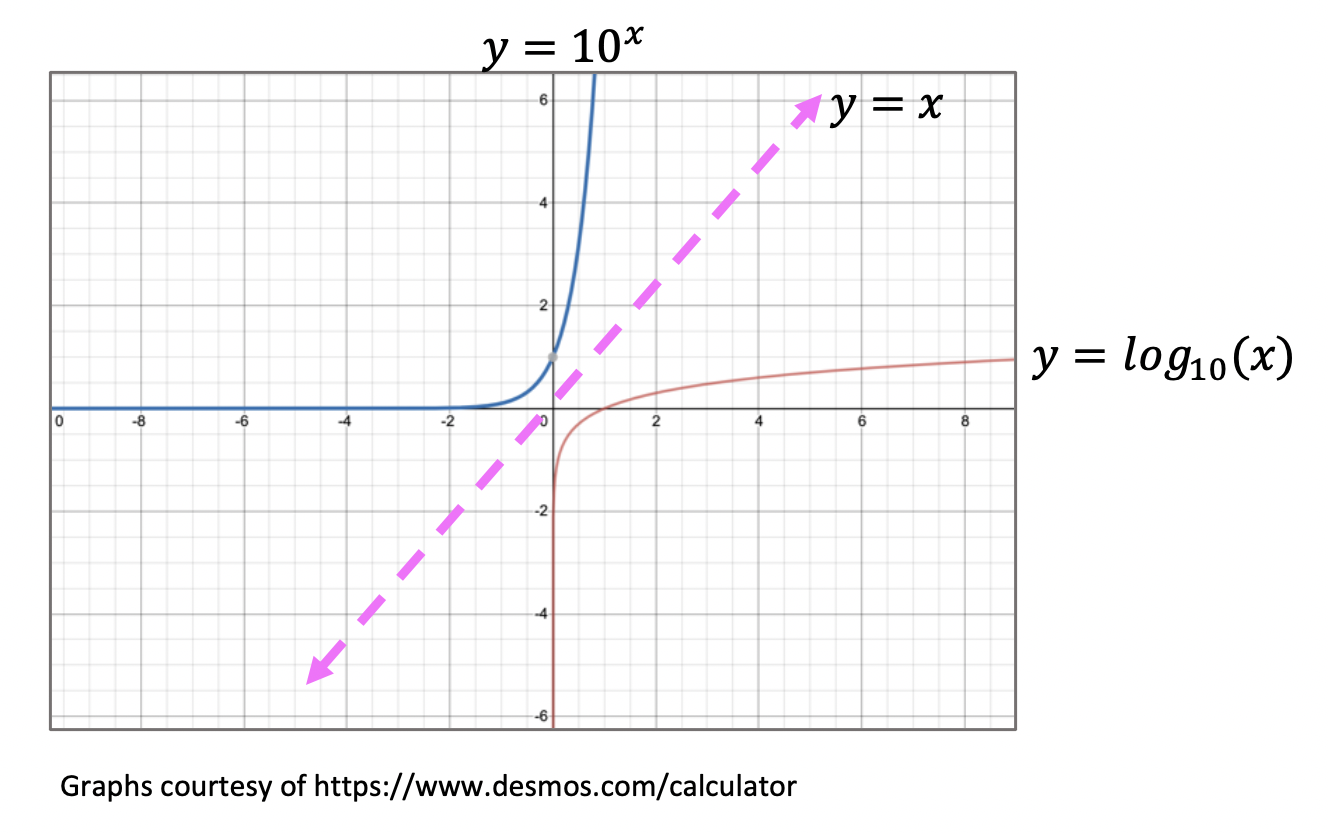
Logarithms are the inverses of exponential functions. This means that when graphed, they are symmetrical along the line y=x. Check it out below!

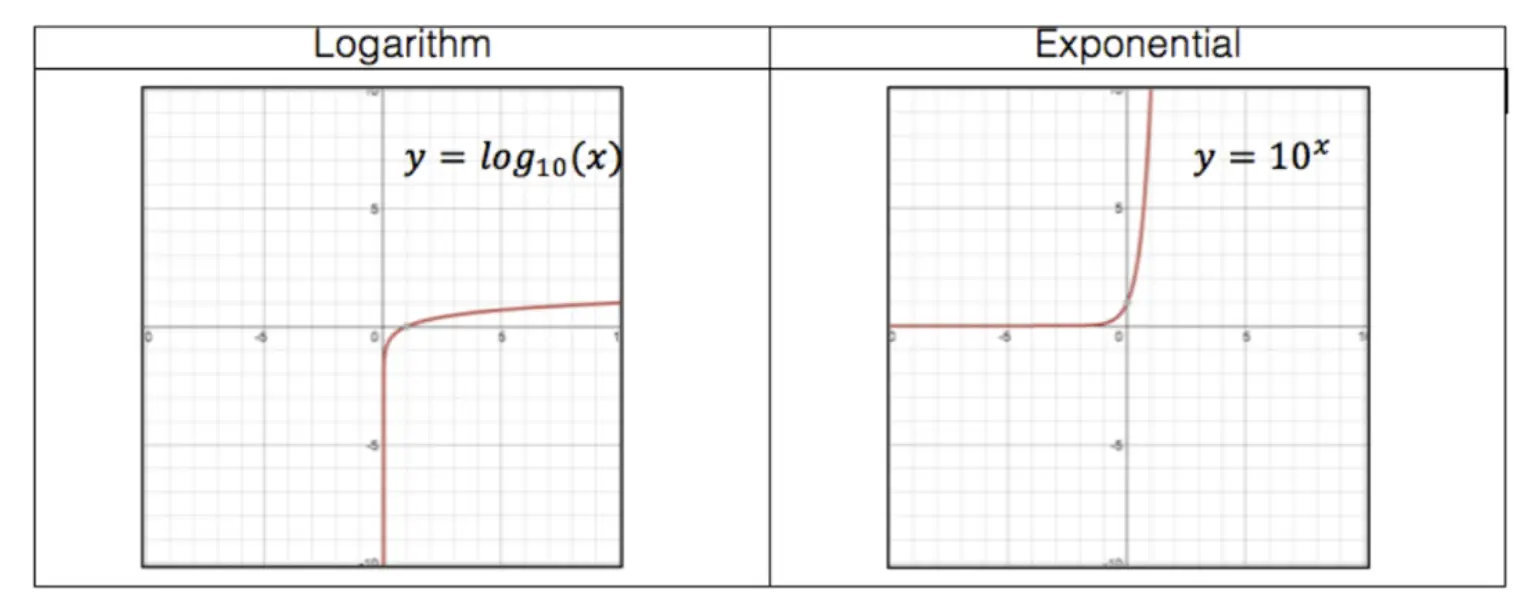
When on the same set of axis, notice how the functions are symmetrical over the line y=x:

We use logarithms to find the unknown values of exponents, such as the x value in the equation,. This is a simple example, where we know the value of x is equal to 2,(). But what if it were to get more complicated? That’s where logs come in!

How to Solve Log Equations?

Logarithms follow a swooping pattern that allows us to write it in exponential form, let’s take a look at some Examples below:

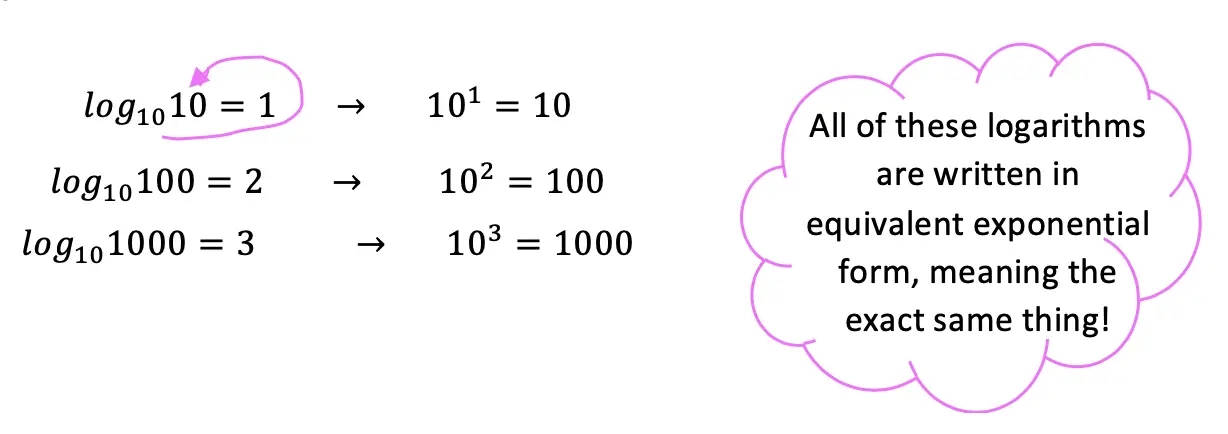
But wait there’s more! Logs have a set of Rules that makes solving log equations a breeze!

We can use these rules to help us algebraically solve logarithmic equations, let’s look at an example that applies the Product Rule.

Example:

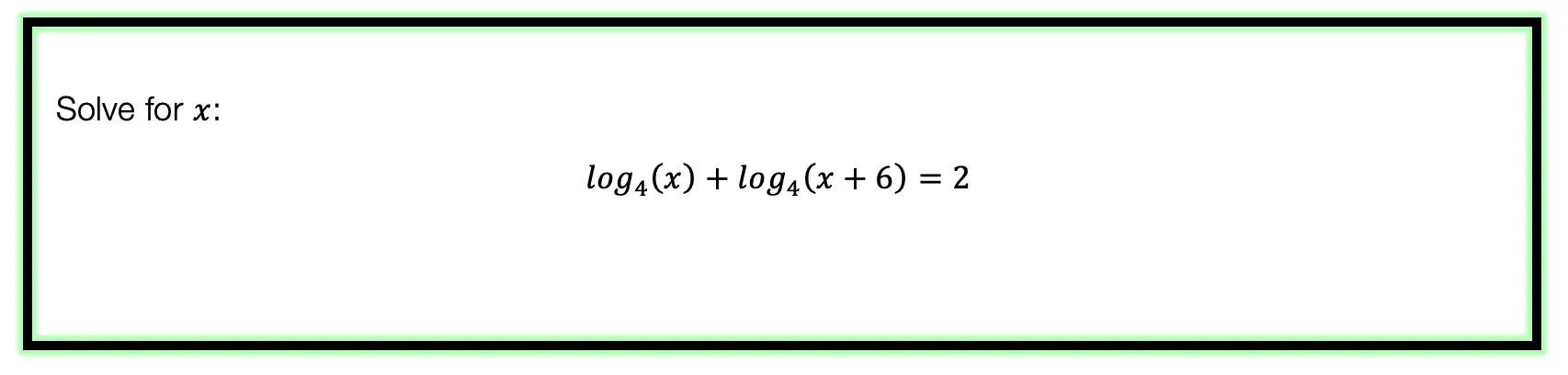
Screen Shot 2020-06-24 at 9.36.08 PM.png

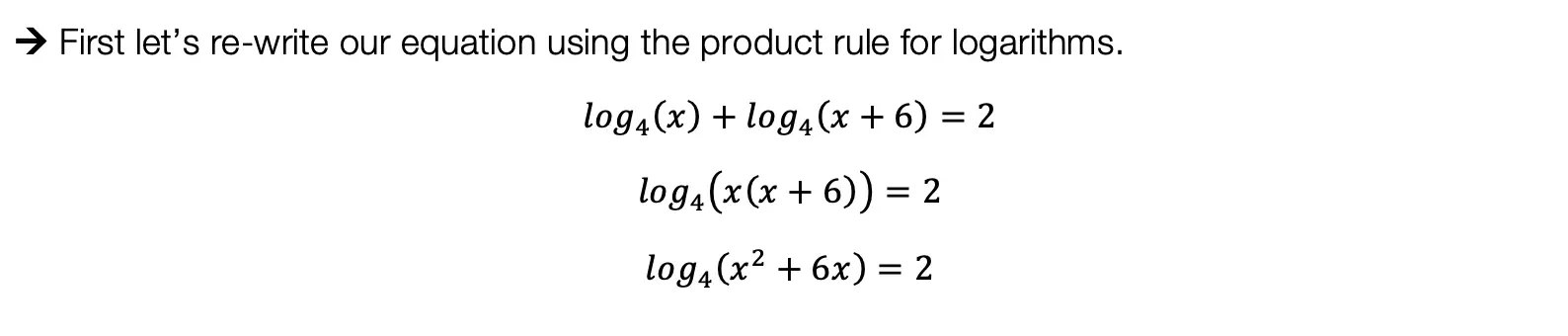
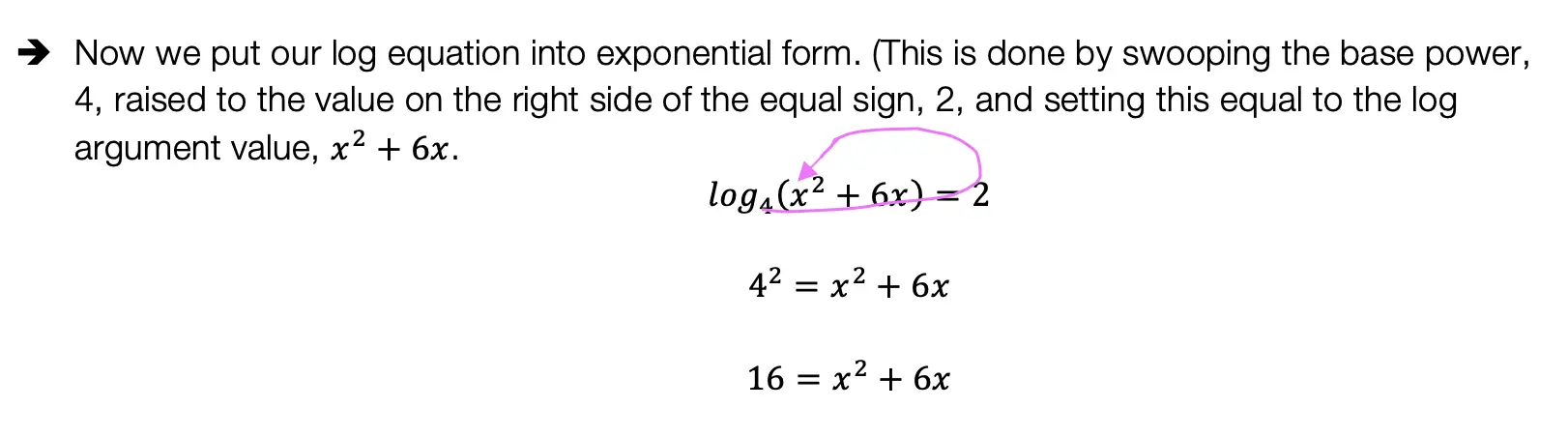
Screen Shot 2020-06-24 at 9.46.07 PM.png

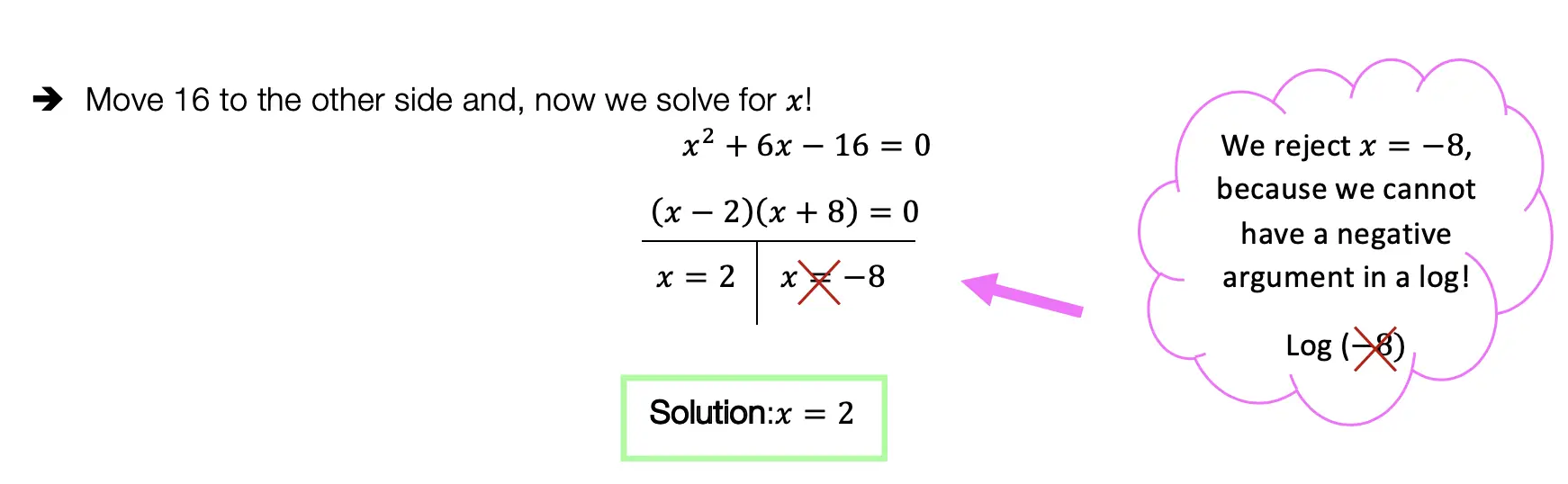
Try the following practice questions on your own!

Practice Questions:

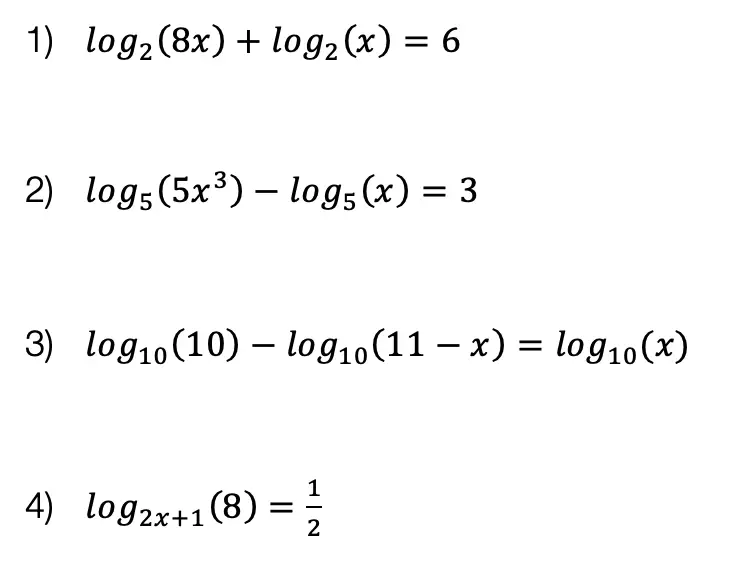
Screen Shot 2020-06-24 at 9.39.16 PM.png

Solutions:

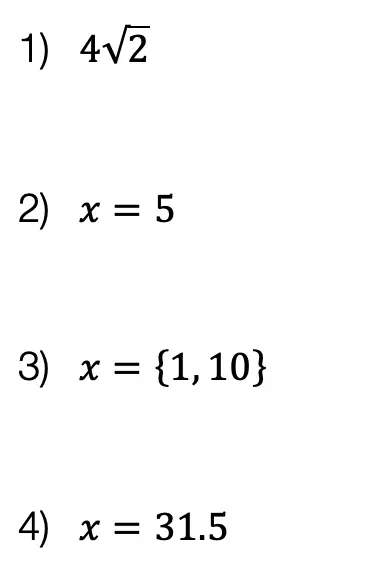
Still got questions? No problem! Check out the video that goes over the same example outlined above. And for more info. on logarithms check out this post that goes over a NYS Regent’s question here. Subscribe below to get the latest FREE math videos, lessons, and practice questions from MathSux. Thanks for stopping by and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

****Check out this Bonus Video on How to Change Log Bases****

Perpendicular & Parallel Lines Through a Given Point: Geometry

Happy Wednesday math friends! Today we’re going to go over the difference between perpendicular and parallel lines, then we’ll use our knowledge of the equation of a line (y=mx+b) to see how to find perpendicular and parallel lines through a given point. This is a common question that comes up on the NYS Geometry Regents and is something we should prepare for, so let’s go!

If you need any further explanation, don’t hesitate to check out the Youtube video below that goes into detail on how to find perpendicular and parallel lines through a given point one step at a time. Happy calculating! 🙂

Perpendicular Lines:

Perpendicular & Parallel Lines Through a Given Point

Perpendicular Lines: Lines that intersect to create a 90-degree angle and can look something like the graph below. Their slopes are negative reciprocals of each other which means they are flipped and negated. See below for example!

Example: Find an equation of a line that passes through the point (1,3) and is perpendicular to line y=2x+1 .

Parallel Lines:

Parallel lines are lines that go in the same direction and have the same slope (but have different y-intercepts). Check out the example below!

Example: Find an equation of a line that goes through the point (-5,1) and is parallel to line y=4x+2.

Try the following practice questions on your own!

Practice Questions:

1) Find an equation of a line that passes through the point (2,5) and is perpendicular to line y=2x+1.

2) Find an equation of a line that goes through the point (-2,4) and is perpendicular to line

3) Find an equation of a line that goes through the point (1,6) and is parallel to line y=3x+2.

4) Find an equation of a line that goes through the point (-2,-2) and is parallel to line y=2x+1.

Solutions:

Need more of an explanation? Check out the video that goes over these types of questions up on Youtube (video at top of post) and let me know if you have still any questions.

Happy Calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more on Perpendicular and parallel lines? Check out this Regents question on perpendicular lines here!

4 Ways to Factor Trinomials: Algebra

Greeting math peeps and welcome to MathSux! In this post, we are going to go over 4 ways to Factor Trinomials and get the same answer, including, (1) Quadratic Formula (2) Product/Sum, (3) Completing the Square, and (4) Graphing on a Calculator. If you’re looking for more don’t forget to check out the video and practice questions below. Happy Calculating! 🙂

Also, if need a review on Factor by Grouping or Difference of Two Squares (DOTS) check out the hyperlinks here!

*If you haven’t done so, check out the video that goes over this exact problem, and don’t forget to subscribe!

We will take this step by step, showing 4 ways to factor trinomials, getting the same answer each and every time! Let’s get to it!

4 Ways to Factor Trinomials

(1) Quadratic Formula:

____________________________________________________________________

(2) Product/Sum:

4 Ways to Factor Trinomials ____________________________________________________________________

(3) Completing the Square:

4 Ways to Factor Trinomials ____________________________________________________________________

(4) Graph:

Choose the factoring method that works best for you and try the practice problems on your own below!

Practice Questions:

Solutions:

Want a review of all the different factoring methods out there? Check out the ones left out here (DOTS and GCF) and happy calculating! 🙂

For even more ways to factor quadratic equations, check out How to factor by Grouping here! 🙂

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring Review

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Imaginary and Complex Numbers

Quadratic Equations with 2 Imaginary Solutions

Focus and Directrix of a Parabola

Also, if you want more Mathsux? Don’t forget to check out our Youtube channel and more below! If you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Median of a Trapezoid Theorem: Geometry

Hi everyone and welcome to Math Sux! In this post, we are going to look at how to use and applythe median of a trapezoid theorem. Thankfully, it is not a scary formula, and one we can easily master with a dose of algebra. The only hard part remaining, is remembering this thing! Take a look below to see a step by step tutorial on how to use the median of a trapezoid theorem and check out the practice questions at the end of this post to truly master the topic. Happy calculating! 🙂

*If you haven’t done so, check out the video that goes over this exact problem, also please don’t forget to subscribe!

Step 1: Let’s apply the Median of a Trapezoid Theorem to this question! A little rusty? No problem, check out the Theorem below.

Median of a Trapezoid Theorem: The median of a trapezoid is equal to the sum of both bases.Step 2: Now that we found the value of x , we can plug it back into the equation for median, to find the value of median

Want more practice? Your wish is my command! Check out the practice problems below:

Practice Questions:

1.is the median of trapezoid ABCDEF, find the value of the median, given the following:2. is the median of trapezoid ACTIVE, find the value of the median, given the following:3.is the median of trapezoid DRAGON, find the value of the median, given the following:

4. is the median of trapezoid MATRIX, find the value of the median, given the following:

Solutions:

Need more of an explanation? Check out the detailed video and practice problems. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Area of a Sector: Geometry

Hi math friends, has anyone been cooking more during quarantine? We all know there is more time for cookin’ and eatin’ cakes but have you ever been curious about the exact amount of cake you are actually eating?! Well, you’re in luck because today we are going to go over how to find the area of a piece of cake, otherwise known as the Area of a Sector!

Now, we’ll all be able to calculate just how much we are overdoing it on that pie! Hopefully, everyone is eating better than I am (I should really calm down on the cupcakes). Ok, now to our question:

*Also, If you haven’t done so, check out the video that goes over this exact problem, and don’t forget to subscribe!

Explanation:

How do I answer this question?

We must apply/adjust the formula for the area of a circle to find the area of the blue shaded region otherwise known as the sector of this circle.

How do we do this?

Before we begin let’s review the formula for the area of a circle. Just a quick reminder of what each piece of the formula represents:

Step 1: Now let’s fill in our formula, we know the radius is 5, so let’s fill that in below:

Step 2: Ok, great! But wait, this is for a sector; We need only a piece of the circle, not the whole thing. In other words, we need a fraction of the circle. How can we represent the area of the shaded region as a fraction?

Well, we can use the given central angle value, , and place it over the whole value of the circle, . Then multiply that by the area of the entire circle. This will give us the value we are looking for!

Step 3: Multiply and solve!

Ready for more? Try solving these next few examples on your own to truly master area of a sector!

Practice Questions:

Find the area of each shaded region given the central angle and radius for each circle:

Solutions:

What do you think of finding the area of sector? Are you going to measure the area of your next slice of pizza? Do you have any recipes to recommend? Let me know in the comments and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more about circles? Check out this post on the circle formula here!

Circle Theorems and Formulas:

Central Angle Theorem

Intersecting Secants Theorem

Inscribed Angles and Intercepted Arc

Circle Theorems

Solving Radical Equations: Algebra 2/Trig.

Today we’re back with Algebra 2, this time solving for radical equations! Did you say “Radical Equations?” As in wild and crazy equations? No, not exactly, radicals in math are used to take the square root, cubed root, or whatever root of a number.

Example #1:

Screen Shot 2020-05-12 at 11.25.03 AM.png

Radicals are actually pretty cool because we can write them a couple of different ways and they all mean the same thing! Check it out below:Still not sure of their coolness? Let’s see what they look like with actual numbers:
Example: Solve the following algebraic equation below for the missing variable (aka, solve for x).Explanation:

How do I answer this question?

The question wants us to solve for x using our knowledge of radicals and algebra. You can also check out how to solve this question on Youtube here!

How do we do this?

Step 1: We start solving this radical equation like any other algebraic problem: by getting x alone. We can do this easily by subtracting 7 and then dividing out 5.

Step 2: Now, to get rid of that pesky radical, we need to square the entire radical. Remember, whatever we do to one side of the equation, we must also do to the other side of the equation, therefore, we also square 14 on the other side of the equal sign. *This gets rid of our radical and allows us to solve for x algebraically as normal!

Screen Shot 2020-05-12 at 11.29.34 AM.png

What happens when there is a cubed root though!?!?

When dividing polynomials with different value roots, raise the entire radical to that same power of root to cancel it out:Remember, we know radicals can also be written as fractions:

Therefore we also know that if we raise the entire radical expression to the same power of the root, the two exponents will cancel each other out:

Example #2:

Want more practice? Try solving radical equations in the next few examples on your own.

Practice:

Screen Shot 2020-05-12 at 11.32.39 AM.png

Solutions:

Screen Shot 2020-05-12 at 11.33.12 AM.png

Looking to brush up on how to solve absolute value equations? Check out the post here! Did I miss anything? Don’t let any questions go unchecked and let me know in the comments! Happy calculating! 🙂

Don’t forget to check out the latest free videos and posts with MathSux and subscribe!

Facebook ~ Twitter ~ TikTok ~ Youtube

Dividing Polynomials: Algebra 2/Trig.

Greeting math peeps! In this post we are going to go over dividing polynomials! At some point, you may need to know how to answer these types of questions. The cool thing about dividing polynomials is that it’s the same long division you did way back in grade school (except now with a lot of x). Ok, let’s get to it and check out the question below:

Also, if you haven’t done so, check out the video related that corresponds to this problem on Youtube below! 🙂

Explanation:

How do I answer this question?

The question wants us to divide polynomials by using long division.

How do we do this?

Step 1: First we set up a good ole’ division problem with the divisor, dividend, and quotient to solve.

Step 2: Now we use long division like we used to back in the day! If you have any confusion about this please check out the video in this post.

What if there’s a Remainder?

What happens when there is a remainder though!?!? When dividing polynomials with a remainder in the quotient, the answer is found and checked in a very similar way! Check it out in the example below:

Notice we represented the remainder by adding to our quotient! We just put the remainder over the divisor to represent this extra bit of solution.

Want more practice? Try solving these next few examples on your own.

Practice Questions:

Screen Shot 2020-05-04 at 10.45.10 PM.png

Solutions:

If you’re looking for more on dividing polynomials, check out this post on synthetic division and finding zeros here!

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Earth Day Fractals!

In honor of Earth Day last week, I thought we’d take a look at some math that appears magically in nature. Math? In nature? For those of you who think math is unnatural or just terrible in general, this is a great time to be proven otherwise!

The key that links math to nature is all about PATTERNS. All math is based on is patterns. This includes all types of math, from sequences to finding x, each mathematical procedure follows some type of pattern. Meanwhile back in the nearest forest, patterns are occurring everywhere in nature.

The rock star of all patterns would have to be FRACTALS. A Fractal is a repeating pattern that is ongoing and has different sizes of the exact same thing! And the amazing thing is that we can actually find fractals in our ~~neighbor’s~~ local garden.

Let’s look at some Fractal Examples:

(1) Romanesco Broccoli: Check out those repeating shapes, that have the same repeating shapes on those shapes and the same repeating shapes on even smaller shapes and…. my brain hurts!

(2) Fern Leaves: The largest part of this fractal is the entire fern leaf itself. The next smaller and identical part is each individual “leaf” along the stem. If you look closely, the pattern continues!

(3) Leaves: If you’ve ever gotten up real close to any type of leaf, you may have noticed the forever repeating pattern that gets smaller and smaller. Behold the power and fractal pattern of this mighty leaf below!

.

Just in case fractals are still a bit hard to grasp, check out the most famous Fractal below, otherwise known as Sierpinski’s Triangle. This example might not be found in your local back yard, but it’s the best way to see what a fractal truly is up close and infinite and stuff.

Looking for more math in nature? Check out this post on the Golden Ratio and happy calculating! 🙂

| Facebook | Twitter |

Perpendicular Lines through a Given Point: Geometry

Ahoy math peeps! I’m writing this during the time of the coronavirus, and although, the NYS Regents tests may be canceled, online zooming is still on! From the good ole’ days of test-taking and sitting in a giant room together, I bring to you a Regent’s classic, a question about how to find perpendicular lines through a given point. We will go over the following Regents question, starting with a review of what perpendicular lines are. Stay curious and happy calculating! 🙂

Perpendicular Lines: When two lines going in opposite directions come together to form a perfect 90º angle! Sounds magical, am I right? Check it out for yourself below:

Perpendicular Lines through a Given Point

A super exciting feature of these so-called perpendicular lines is that their slopes are negative reciprocals of each other. Wait, what?

How do we do this? Now it is time to go back and answer our question!

First, our equation 2y+3x=1 looks kind of cray, so let’s get it back to normal in y=mx+b form:

Need more of an explanation? Check out the video that goes over these types of questions up on Youtube (video at top of post) and let me know if you have still any questions.

Happy Calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more on Perpendicular and parallel lines? Check out the difference between the two in this post here!

COVID-19: What does #FlattenTheCurve even mean?

COVID-19: What does #FlattenTheCurve even mean? If you are a human on Earth, then I’m sure you’ve heard about the coronavirus and are currently social distancing. Here in NYC, I’m quarantining like everyone else and listening to all the beautiful math language that has suddenly become mainstream (so, exciting)! #FlattenTheCurve has become NY’s new catchphrase and for anyone confused about what that means, you’ve come to the right place!

The coronavirus spreads at an Exponential Rate, which means it spreads in a way that increases faster and faster every day.

What does this mean?

For Example, one person with the virus can easily spread the virus to 5 other people, those 5 people can then spread the virus to another 5 people each for a total of an extra 25 people, these 25 people can then spread it to another 5 people each for an extra 125 infected people! And the pattern continues……. See below to get a clearer picture:

COVID-19: What does #FlattenTheCurve even mean?

. *Note: These numbers are not based on actual coronavirus data

The Example we just went over is equal to the exponential equation , but it is only that, an Example! The exact pattern and exponential equation of the future progress of the virus is unknown! We mathematicians, can only measure what has already occurred and prepare/model for the future. To make the virus spread less rapidly, it is our duty to stay home to slow the rate of this exponentially spreading virus as much as possible.

We want to #FlattenTheCurve a.k.a flatten the increasing exponential curve of new coronavirus cases that appear every day! Hopefully, this post brings some clarity to what’s going on in the world right now. Even with mathematics, the true outcome of the virus may be unknown, but understanding why we are all at home in the first place and the positive impact it has is also important (and kind of cool).

Stay safe math friends and happy calculating! 🙂

Want to make math suck just a little bit less? Subscribe and follow us for FREE fun colorful math videos and lessons every week! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube