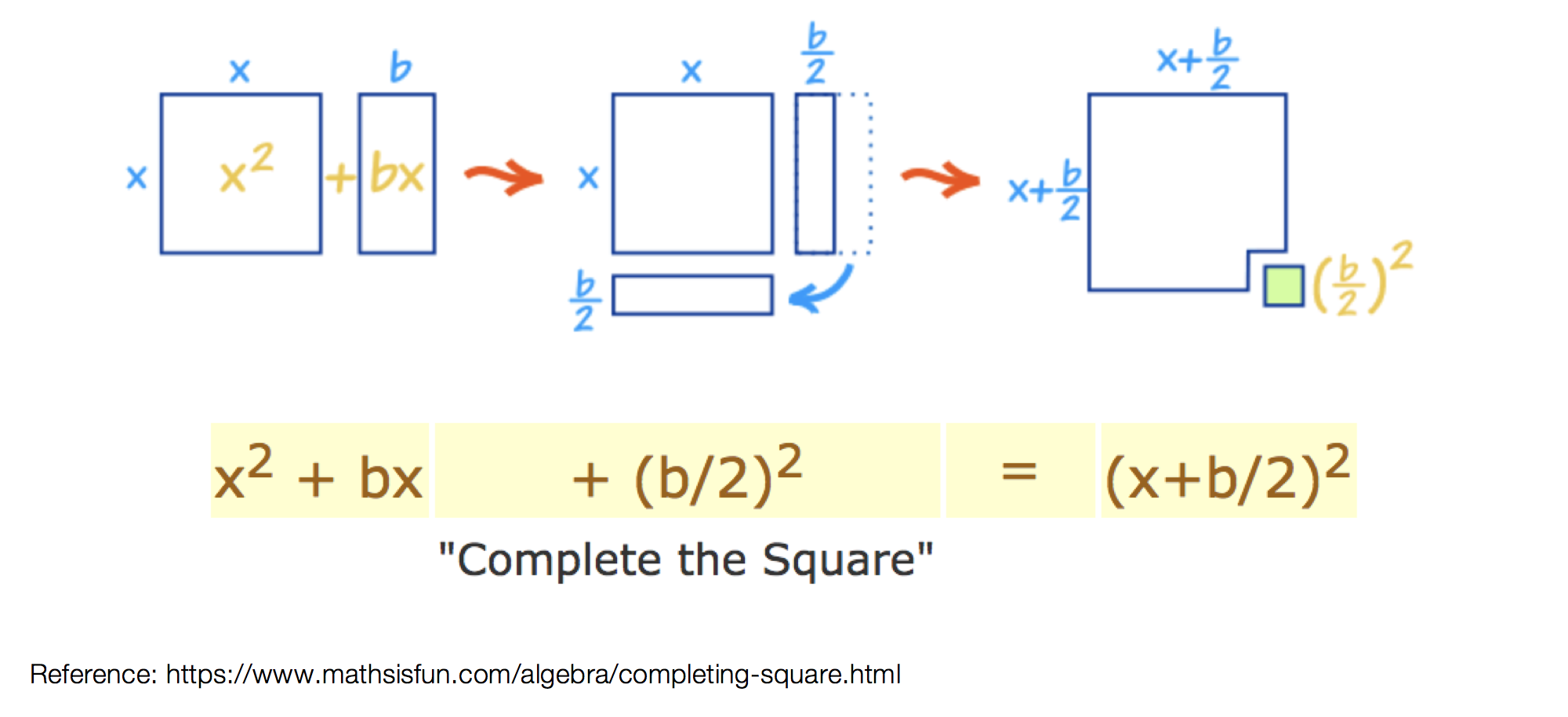
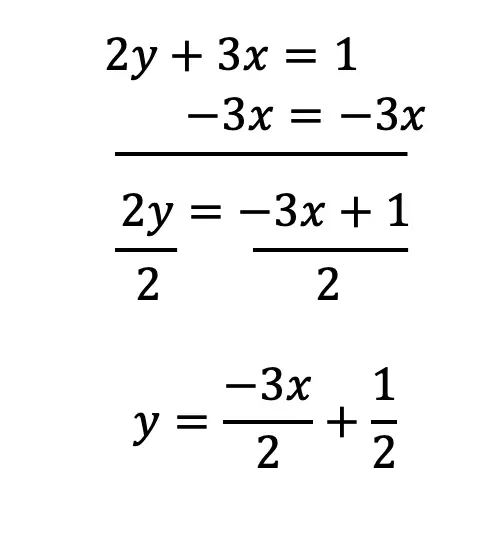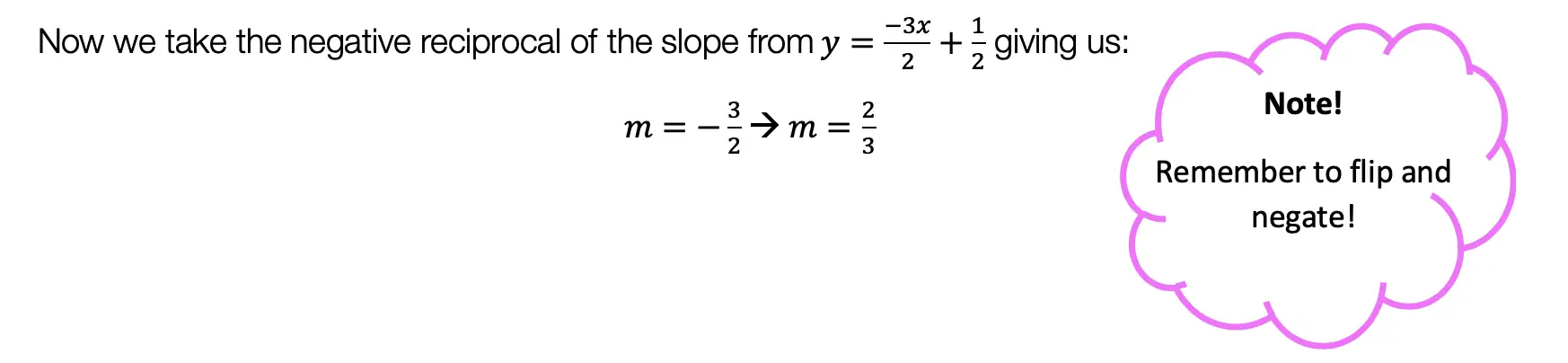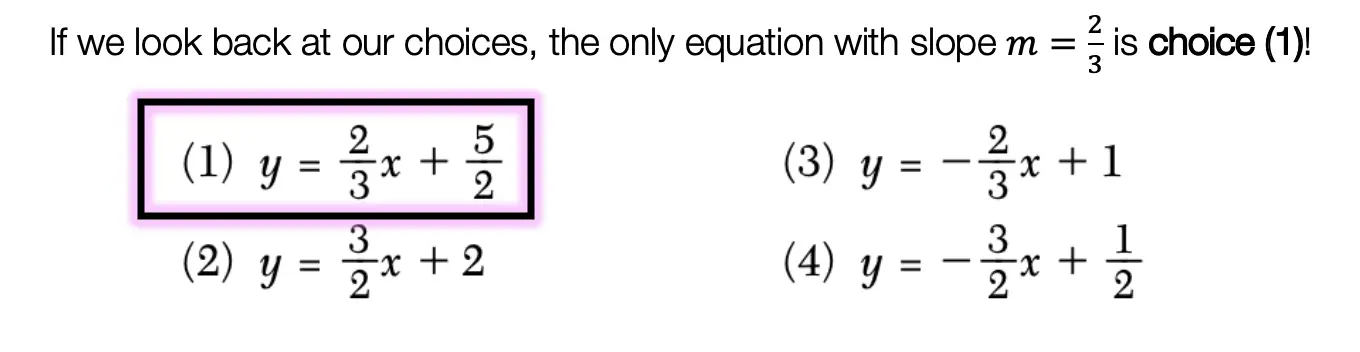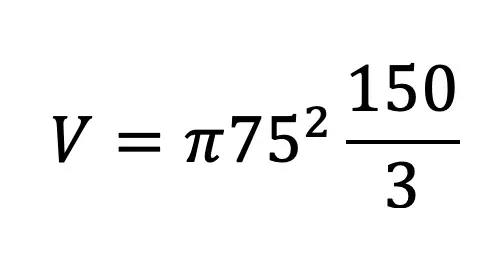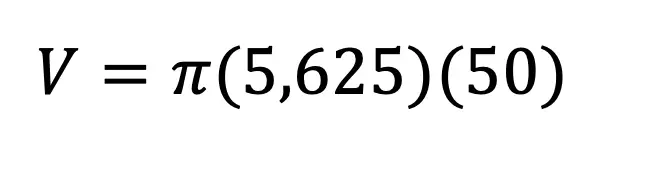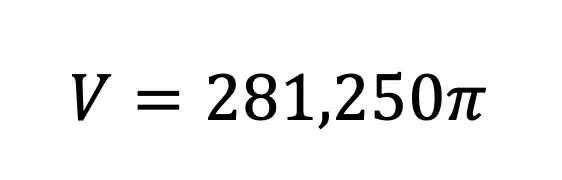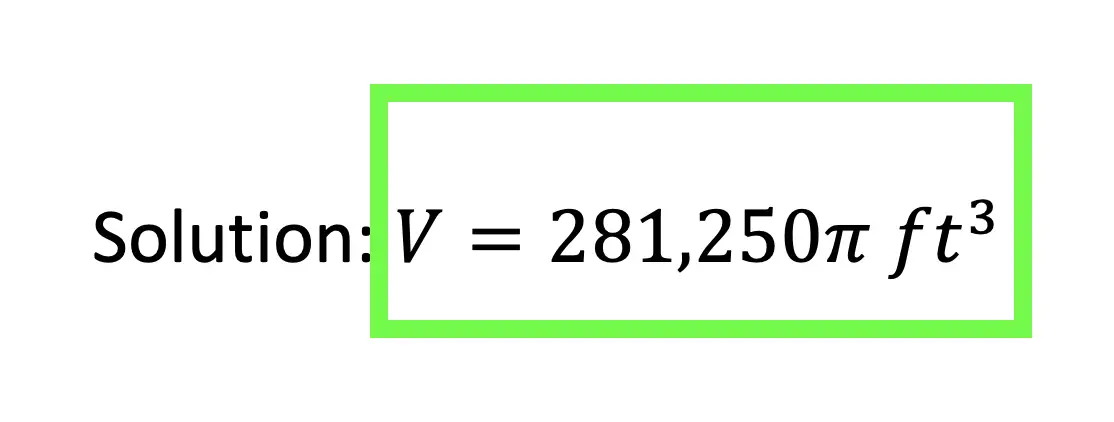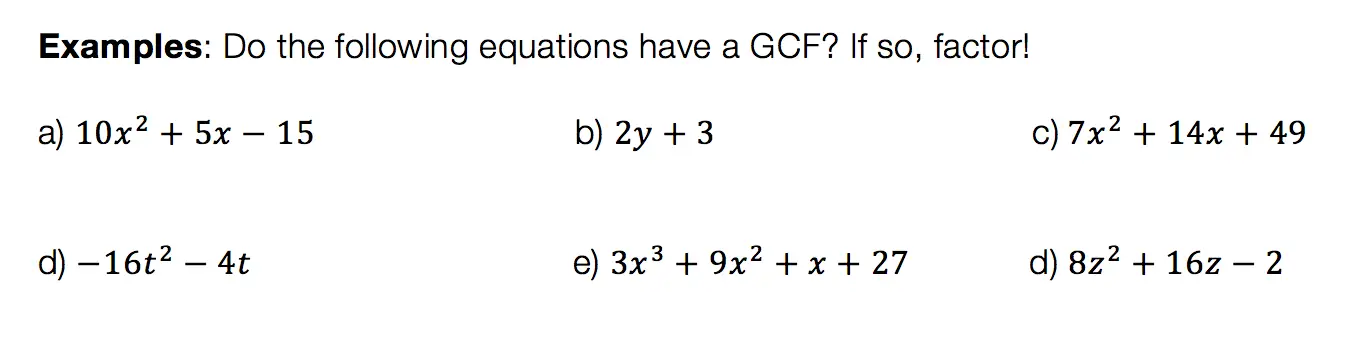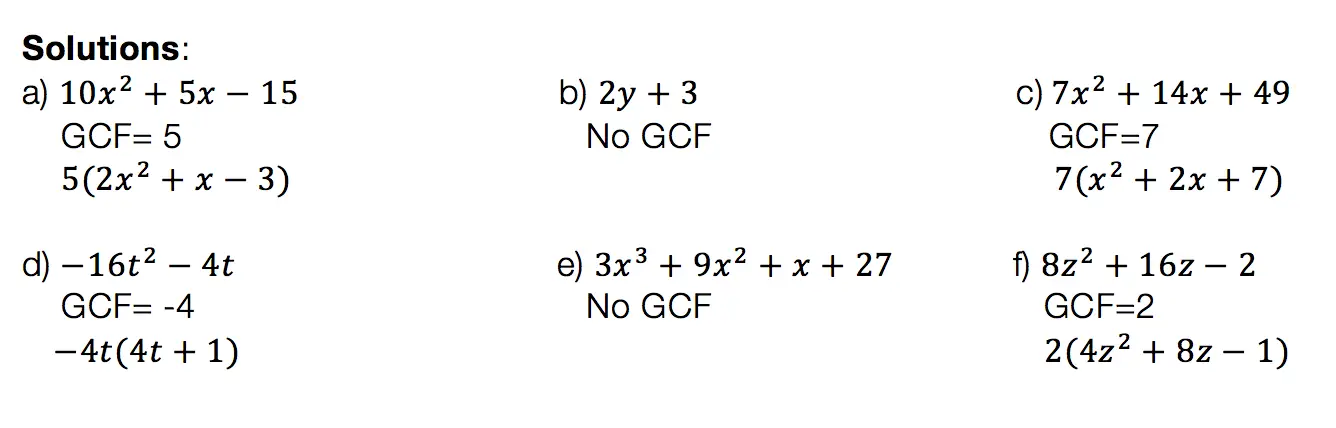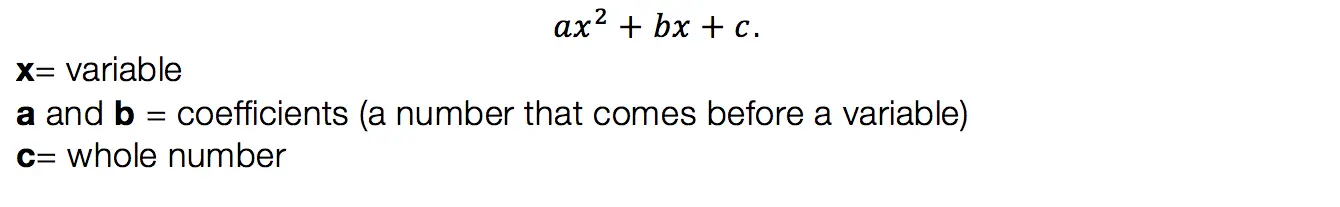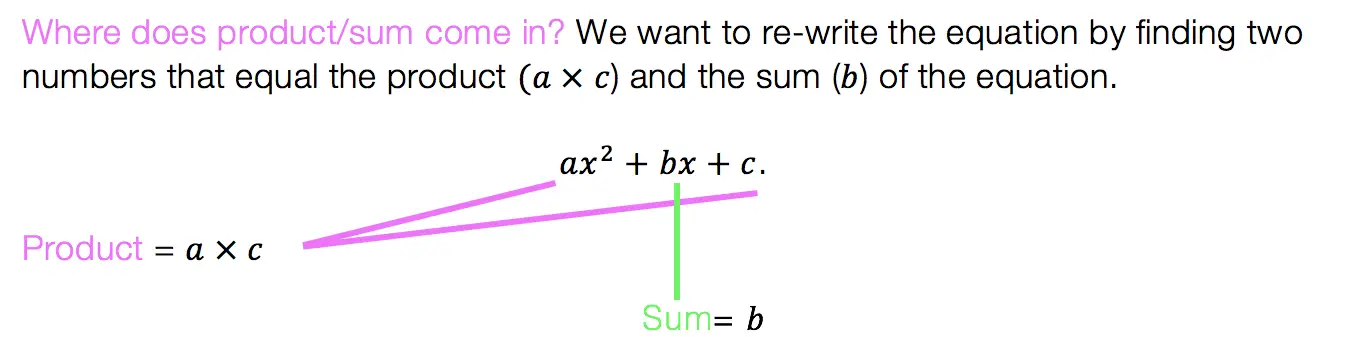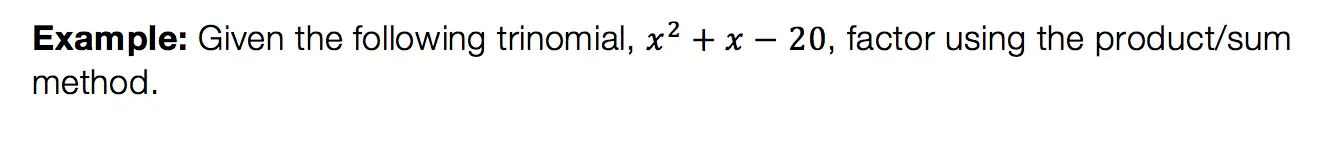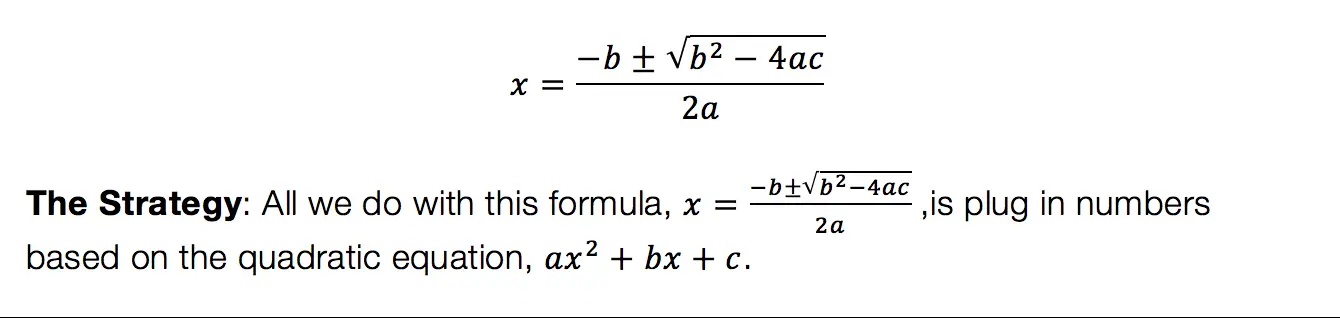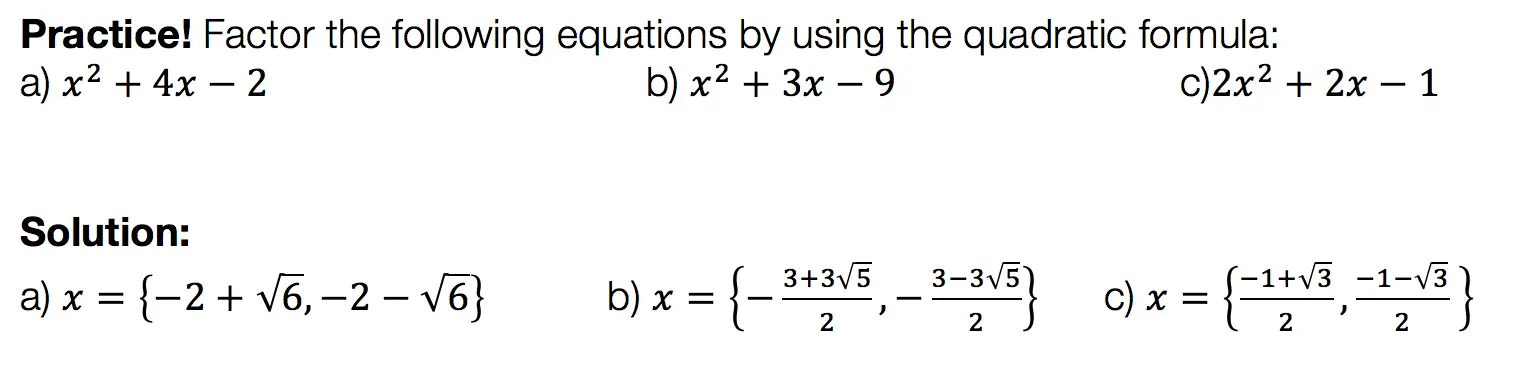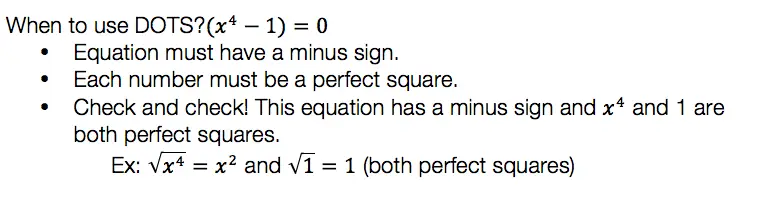Tutoring Archives - Page 2 of 2

Median of a Trapezoid Theorem: Geometry

Hi everyone and welcome to Math Sux! In this post, we are going to look at how to use and applythe median of a trapezoid theorem. Thankfully, it is not a scary formula, and one we can easily master with a dose of algebra. The only hard part remaining, is remembering this thing! Take a look below to see a step by step tutorial on how to use the median of a trapezoid theorem and check out the practice questions at the end of this post to truly master the topic. Happy calculating! 🙂

*If you haven’t done so, check out the video that goes over this exact problem, also please don’t forget to subscribe!

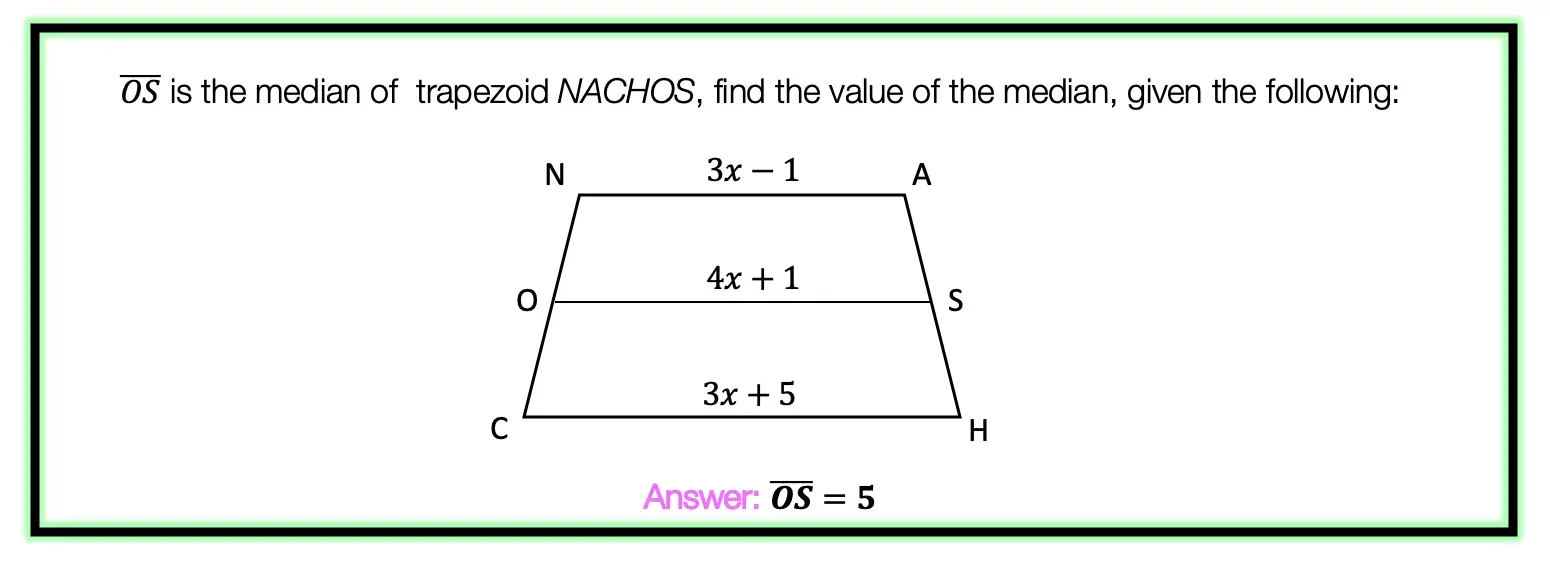
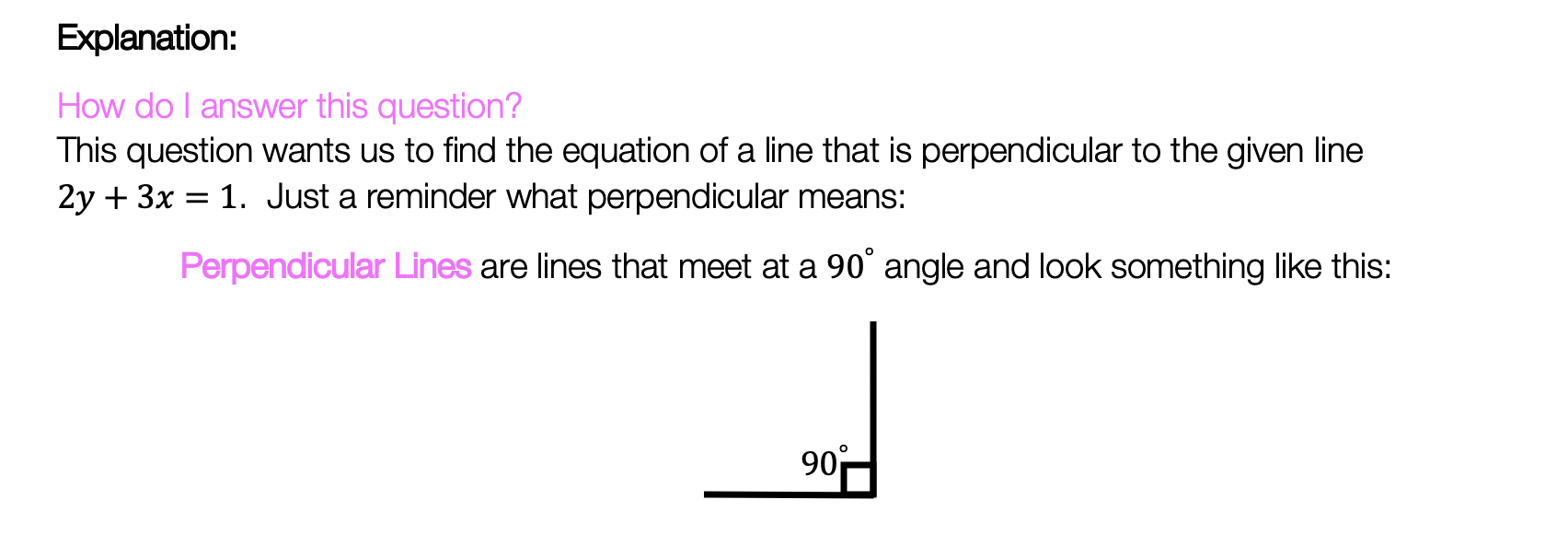
Step 1: Let’s apply the Median of a Trapezoid Theorem to this question! A little rusty? No problem, check out the Theorem below.

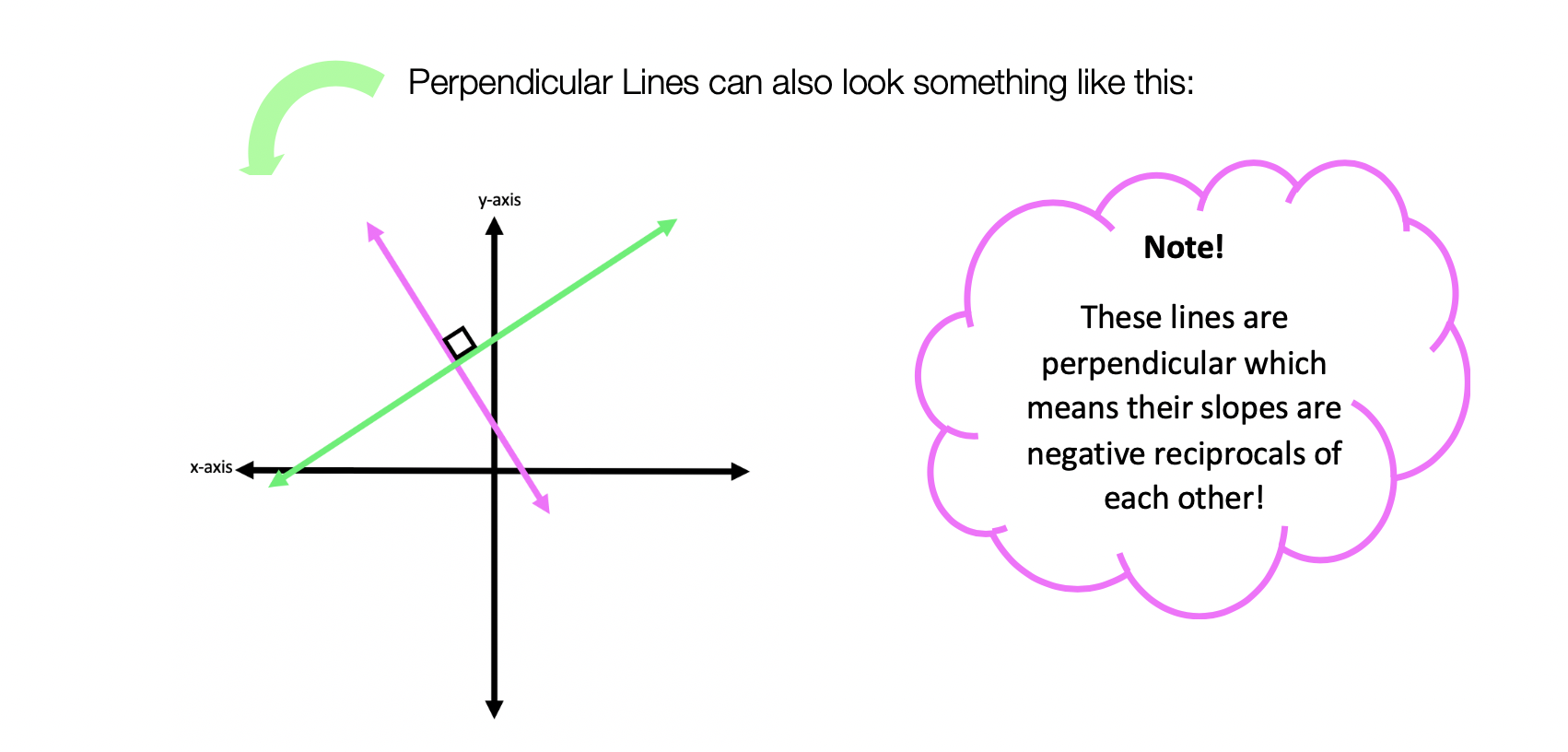
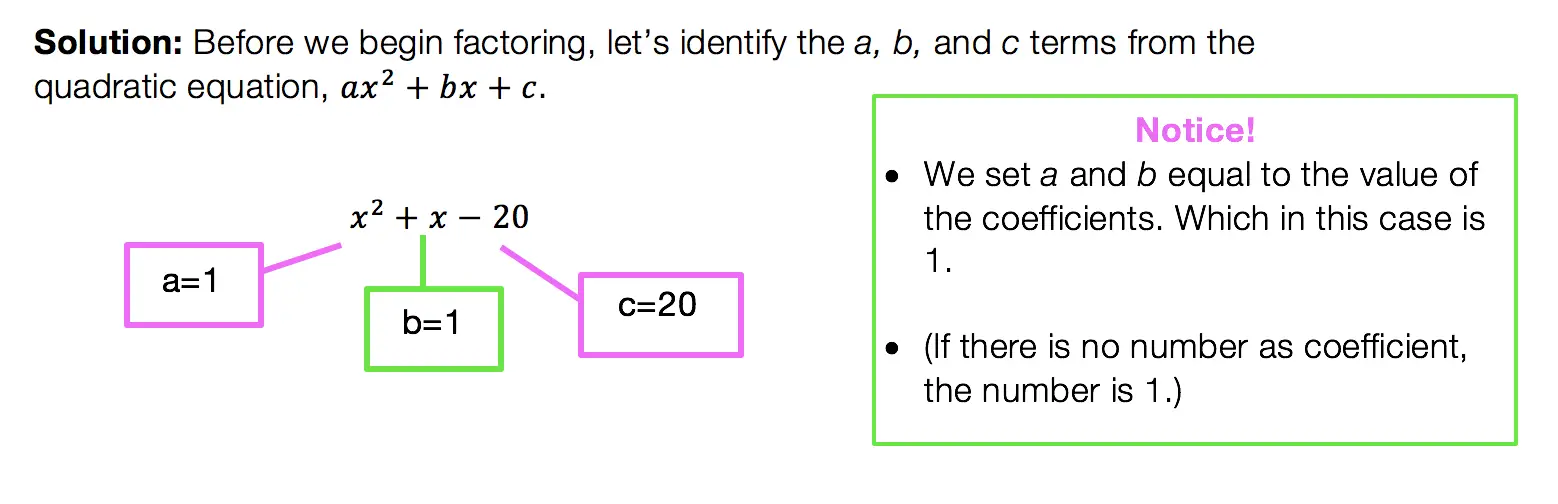
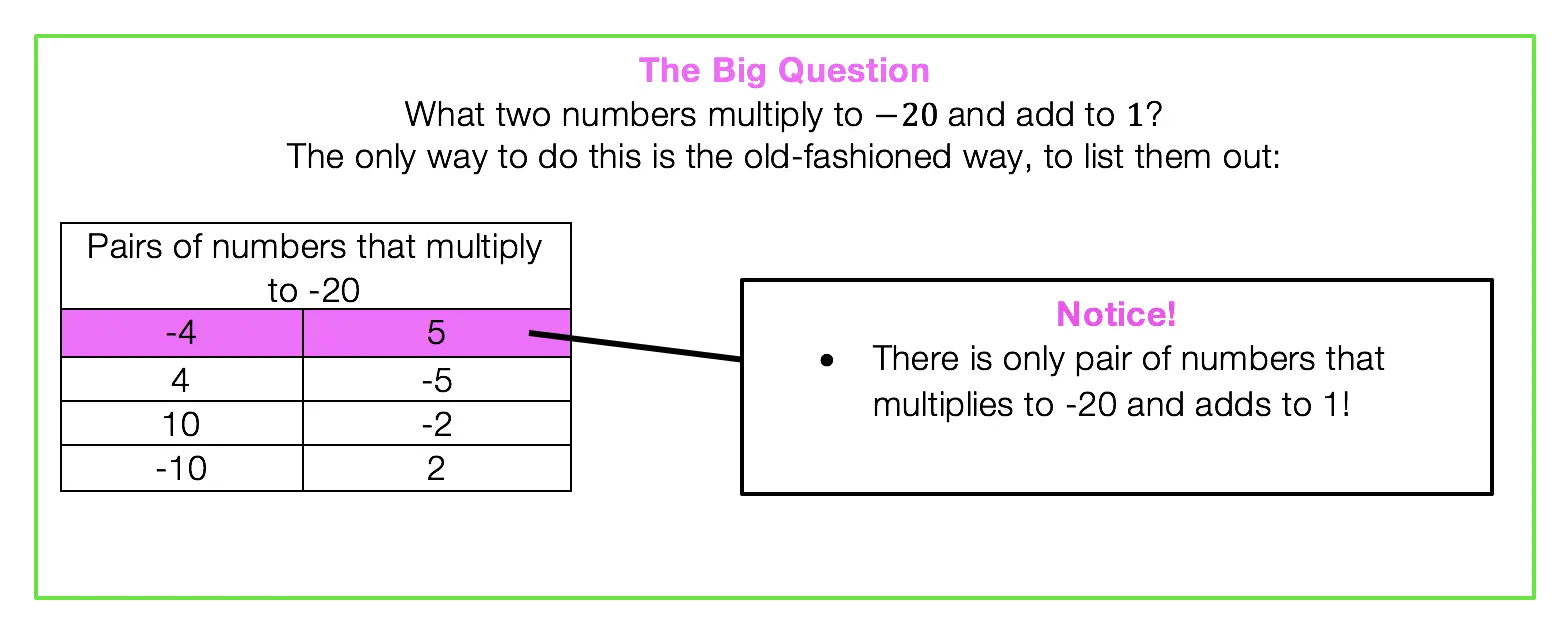
Median of a Trapezoid Theorem: The median of a trapezoid is equal to the sum of both bases.Step 2: Now that we found the value of x , we can plug it back into the equation for median, to find the value of median

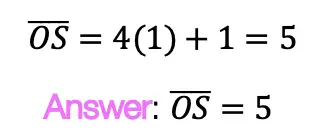
Want more practice? Your wish is my command! Check out the practice problems below:

Practice Questions:

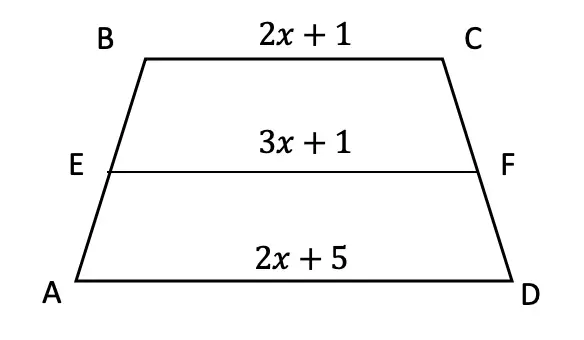
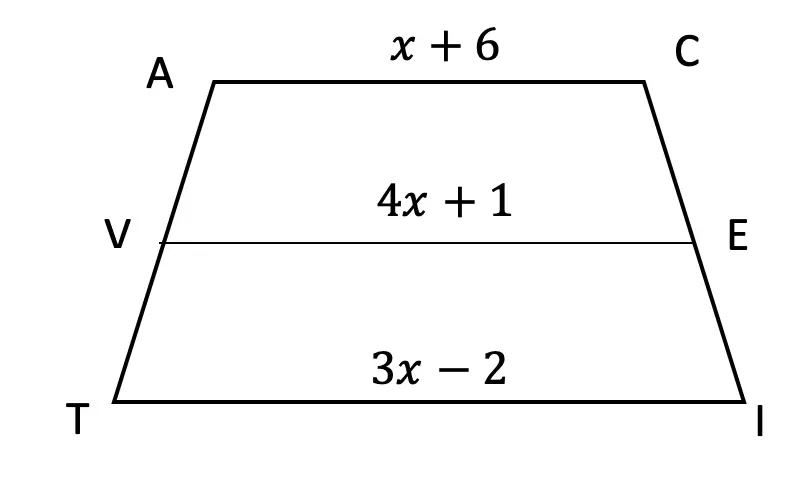
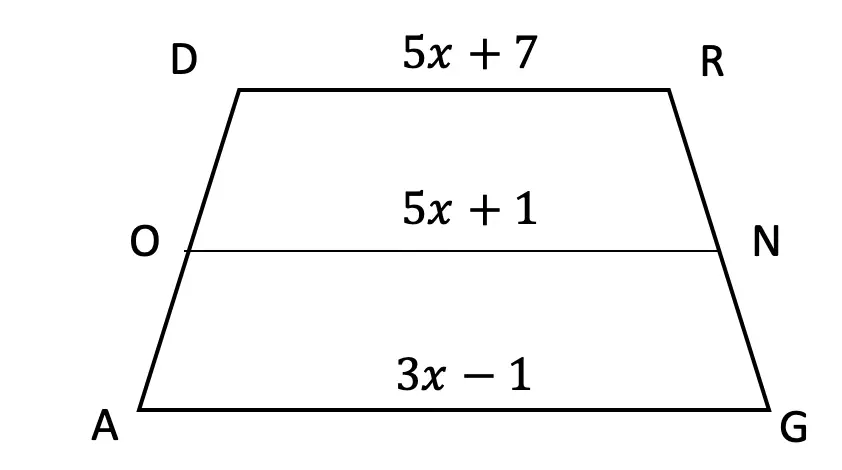
1.is the median of trapezoid ABCDEF, find the value of the median, given the following:2. is the median of trapezoid ACTIVE, find the value of the median, given the following:3.is the median of trapezoid DRAGON, find the value of the median, given the following:

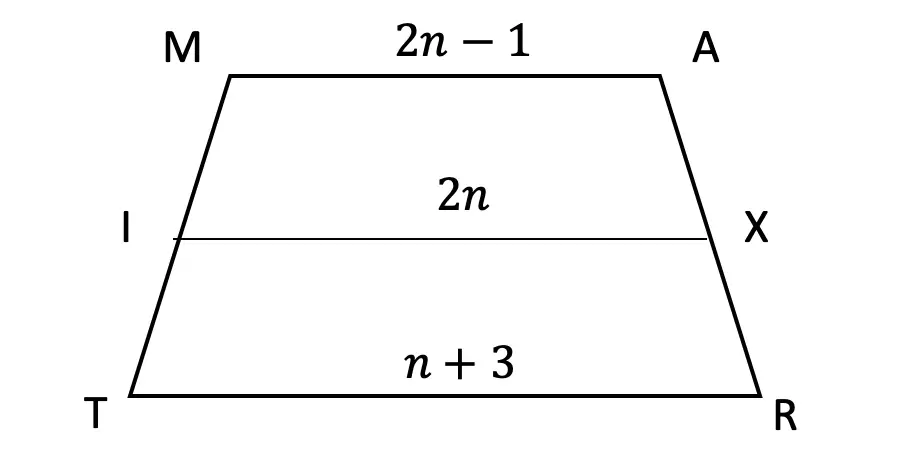
4. is the median of trapezoid MATRIX, find the value of the median, given the following:

Solutions:

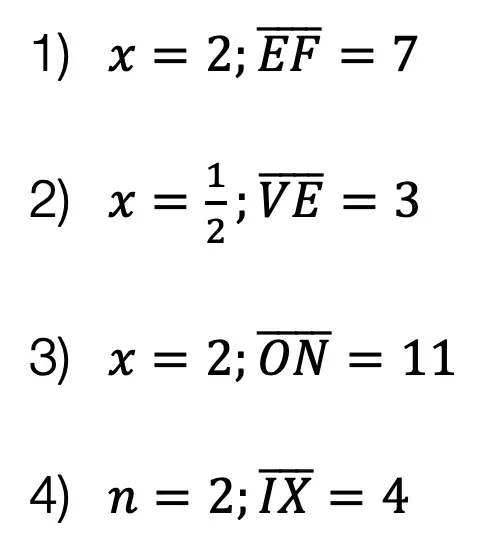
Need more of an explanation? Check out the detailed video and practice problems. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Perpendicular Lines through a Given Point: Geometry

Ahoy math peeps! I’m writing this during the time of the coronavirus, and although, the NYS Regents tests may be canceled, online zooming is still on! From the good ole’ days of test-taking and sitting in a giant room together, I bring to you a Regent’s classic, a question about how to find perpendicular lines through a given point. We will go over the following Regents question, starting with a review of what perpendicular lines are. Stay curious and happy calculating! 🙂

Perpendicular Lines: When two lines going in opposite directions come together to form a perfect 90º angle! Sounds magical, am I right? Check it out for yourself below:

Perpendicular Lines through a Given Point

A super exciting feature of these so-called perpendicular lines is that their slopes are negative reciprocals of each other. Wait, what?

How do we do this? Now it is time to go back and answer our question!

First, our equation 2y+3x=1 looks kind of cray, so let’s get it back to normal in y=mx+b form:

Need more of an explanation? Check out the video that goes over these types of questions up on Youtube (video at top of post) and let me know if you have still any questions.

Happy Calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more on Perpendicular and parallel lines? Check out the difference between the two in this post here!

Math Resources (in the time of COVID)

Calling all students, teachers, and parents! As everyone is stuck at home during a global pandemic, now is a ~~great~~ time we are all forced to try and understand math (and our sanity level) a little bit more. Well, I may not be able to help you with the keeping sanity stuff, but as far as math goes, hopefully, the below math resources offer some much needed mathematic support.

All jokes aside I hope everyone is staying safe and successfully social distancing. Stay well, math friends! 🙂

Kahn Academy: The same Kahn Academy we know and love still has amazing videos and tutorials as usual, but now they also have a live “homeroom” chat on Facebook LIVE every day at 12:00pm. The chats occur daily with Kahn Academy founder Sal and at times feature famous guests such as Bill Gates. Click the link below for more:

Khan Academy Homeroom

Study.com: In a time when companies are being more generous, Study.com is here for us as they offer up to 1000 licenses for school districts and free lessons for teachers, students, and parents. Check out all the education freebies here:

Study.com

Math Planet: If you’re looking for free math resources in Pre-Algebra, Algebra, Algebra 2, and Geometry then you will find the answers you need at Math Planet. All free all the time, find their website here:

MathPlanet

MathSux: Clearly, I had to mention MathSux, the very site you are on right now! Check out free math videos, lesson, practice questions, and more for understanding math any way that works for you!

MathSux

What is your favorite educational site? Let me know in the comments, and stay well! 🙂

Volume of a Cone: Geometry

The Voluminous “Vessel” at Hudson Yards

Calling all NYC dwellers! Have you seen the new structure at Hudson Yards? A staircase to nowhere, this bee-hive like structure is for the true adventurists at heart; Clearly, I had to check it out!

Where does math come in here you say? Well, during my exploration, I had to wonder (as am sure most people do) what is the volume of this almost cone-like structure? It seemed like the best way to estimate the volume here, was to use the formula for the volume of a cone!

What do you think the Volume is?

Volume of a Cone:

I estimated the volume by using the formula of a three-dimensional cone. (Not an exact measurement of the Vessel, but close enough!) .

We can find the radius and height based on the given information above. Everything we need for our formula is right here!

Now that we have our information, let’s fill in our formula and calculate!

Extra Tip! Notice that we labeled the solution with feet cubed , which is the short-handed way to write “feet cubed.” Why feet cubed instead of feet squared? Or just plain old feet? When we use our formula we are multiplying three numbers all measured in feet:

radius X radius X (Height/3)

All three values are measured in feet! –> Feet cubed ()

____________________________________________________________________________________

Did you get the same answer? Did you use a different method or have any questions? Let me know in the comments and happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking to apply more math to the real world? Check out this post on the Golden Ratio here!

How to Factor Quadratic Equations: Algebra

In this post, we are going to dive deep into how to factor Quadratic equations! There are so many different methods to choose from including GCF, Product/Sum, DOTS, and the Quadratic Formula. Here we will go step by step into each method on how to factor quadratic equations, each with their own set of practice questions. For a review on how to factor by grouping, check out this post here and happy calculating! 🙂

Why factor in the first place, you may say? We want to manipulate the equation until we solve for x. Solving for x is our main goal, and factoring allows us to do that. Now let’s get to the good stuff!

How to factor quadratic equations

Greatest Common Factor (GCF):

The greatest common factor is the highest possible number that can be divided out from an equation. This gets the equation into its simplest form and makes it easier for us to solve for x.

Before considering which type of factoring methdo to use, always ask yourself, “Can I take out a GCF?”

How to factor quadratic equations

Product/Sum:

This factoring method is for quadratic equations only! That means the equation takes on the following form:

How to factor quadratic equations

Difference of Two Squares DOTS)

Not to play favorites or anything, but DOTS is the easiest and most lovable of the factoring methods. This factoring method just makes you feel all warm and fuzzy inside or maybe that’s just me). Before we get into how to do DOTS, let’s talk about when?

Quadratic Formula:

We have heard of the quadratic equations, so how id the quadratic formula different?

The Answer: The Quadratic Formula is what we use to factor any trinomial. You can use product/sum on trinomials like we discussed earlier, but this may not always work out easy. The Quadratic Formila on the other hand will work every time!

Low and behold, the Quadratic Formula:

Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂

Looking for more on Quadratic Equations and functions? Check out the following Related posts!

Factoring

Factor by Grouping

Completing the Square

The Discriminant

Is it a Function?

Quadratic Equations with 2 Imaginary Solutions

Imaginary and Complex Numbers

Focus and Directrix of a Parabola

Facebook ~ Twitter ~ TikTok ~ Youtube

Why Must We Complete the Square?: Algebra

Completing the Square: So many steps, such little time. It sounds like it involves a square or maybe this is a geometry problem? Why am I doing this again? Why must we complete the square in the first place?

These are all the thoughts that cross our minds when first learning how to complete the square. Well, I’m here to tell you there is a reason for all those steps and they aren’t that bad if you really break them down, let’s take a look!

Answer: x={-7,3}

Explanation:

I’m not going to lie to you here, there are a lot of seemingly meaningless steps to completing the square. The truth is though (as shocking as it may be), is that they are not meaningless, they do form a pattern, and that there is a reason! Before we dive into why let’s look at how to solve this step by step:

Feeling accomplished yet!? Confused? All normal feelings. There are many steps to this process so go back and review, practice, and pay close attention to where things get fuzzy.

But the big question is why are we doing these steps in the first place? Why does this work out, to begin with?

For those of you who are curious, continue to read below!

Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating!

Need more of an explanation? Check out why we complete the square in the first place here !

Facebook ~ Twitter ~ TikTok ~ Youtube

Pre-Calc: The Factor Theorem

Screen Shot 2016-07-13 at 1.24.54 PM Screen Shot 2016-07-13 at 1.25.01 PM Screen Shot 2016-07-13 at 1.47.17 PM Screen Shot 2016-07-13 at 1.59.19 PM Screen Shot 2016-07-13 at 2.22.51 PM Screen Shot 2016-07-13 at 1.58.24 PM Screen Shot 2016-07-13 at 2.00.38 PM Screen Shot 2016-07-13 at 2.23.48 PM Screen Shot 2016-07-13 at 2.05.51 PM