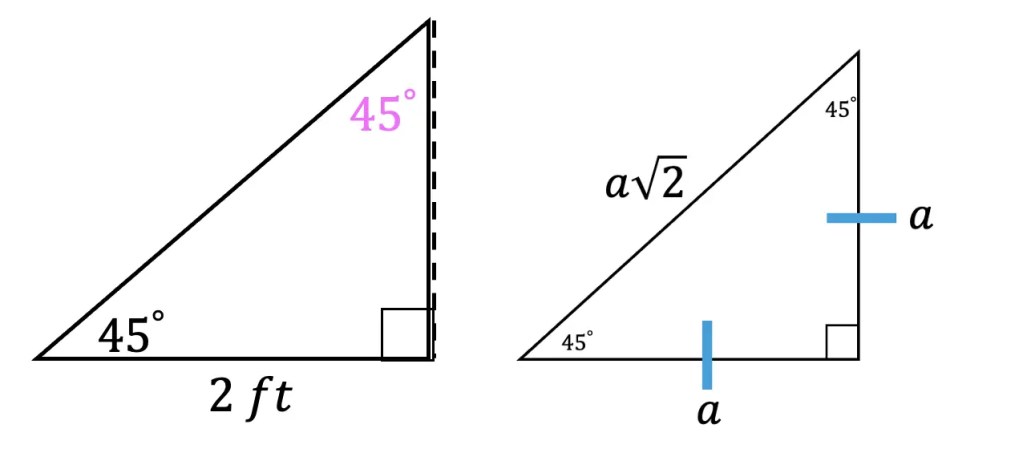
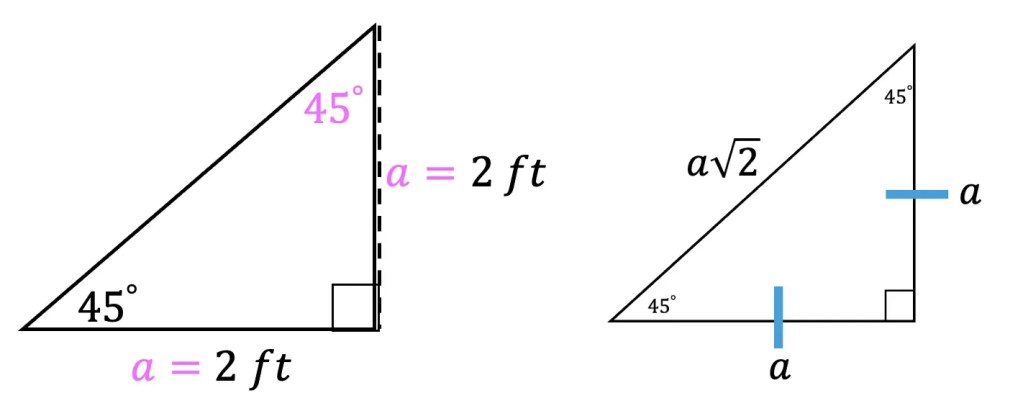
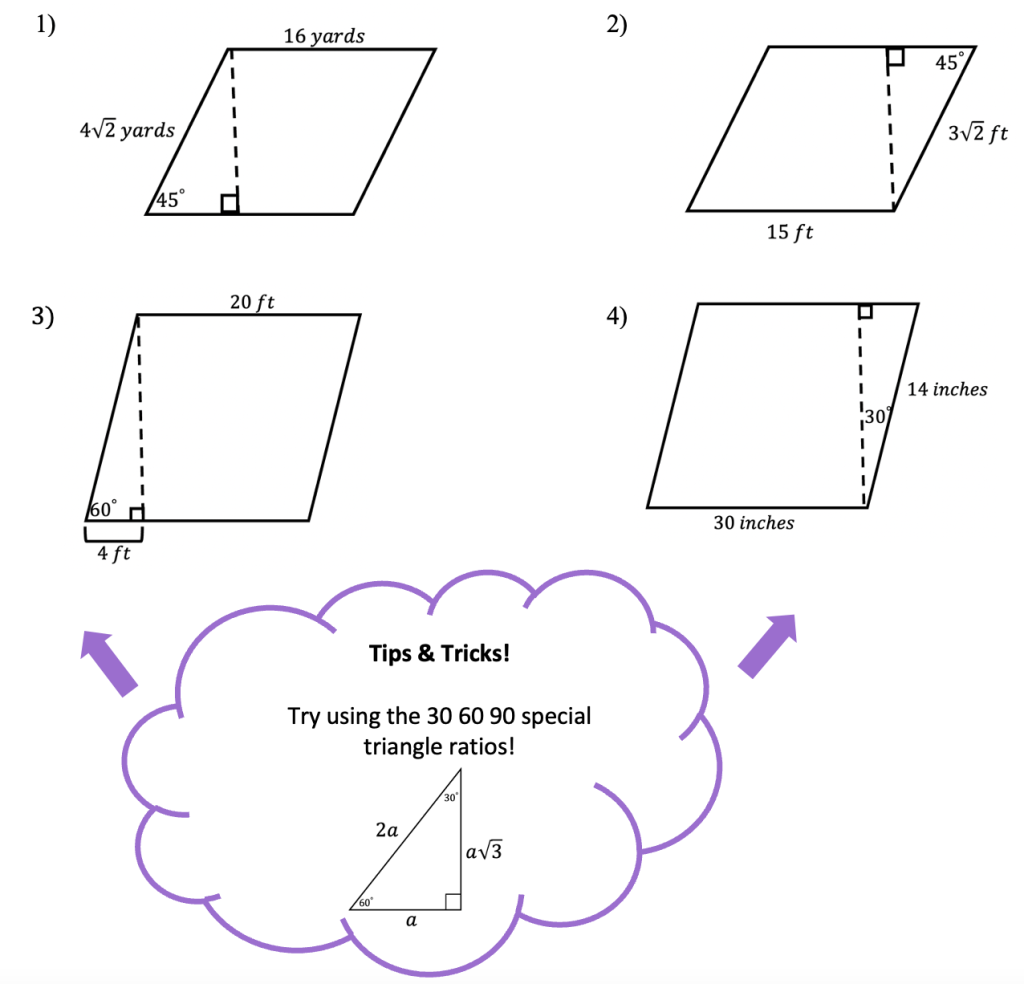
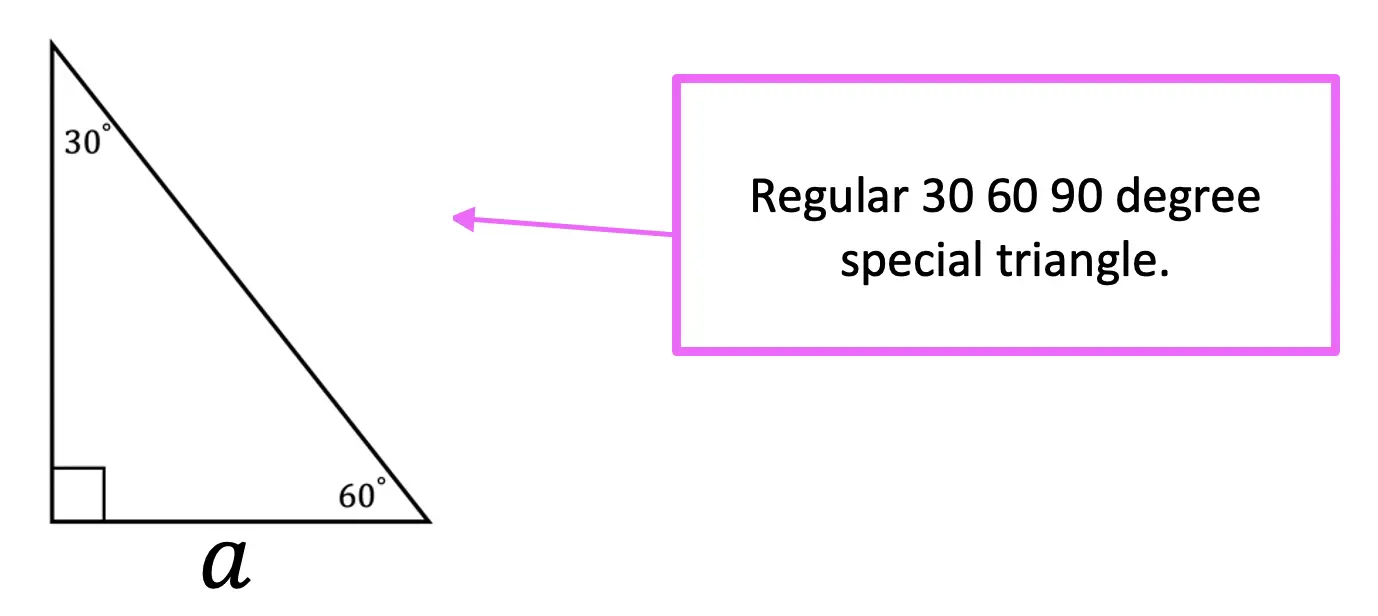
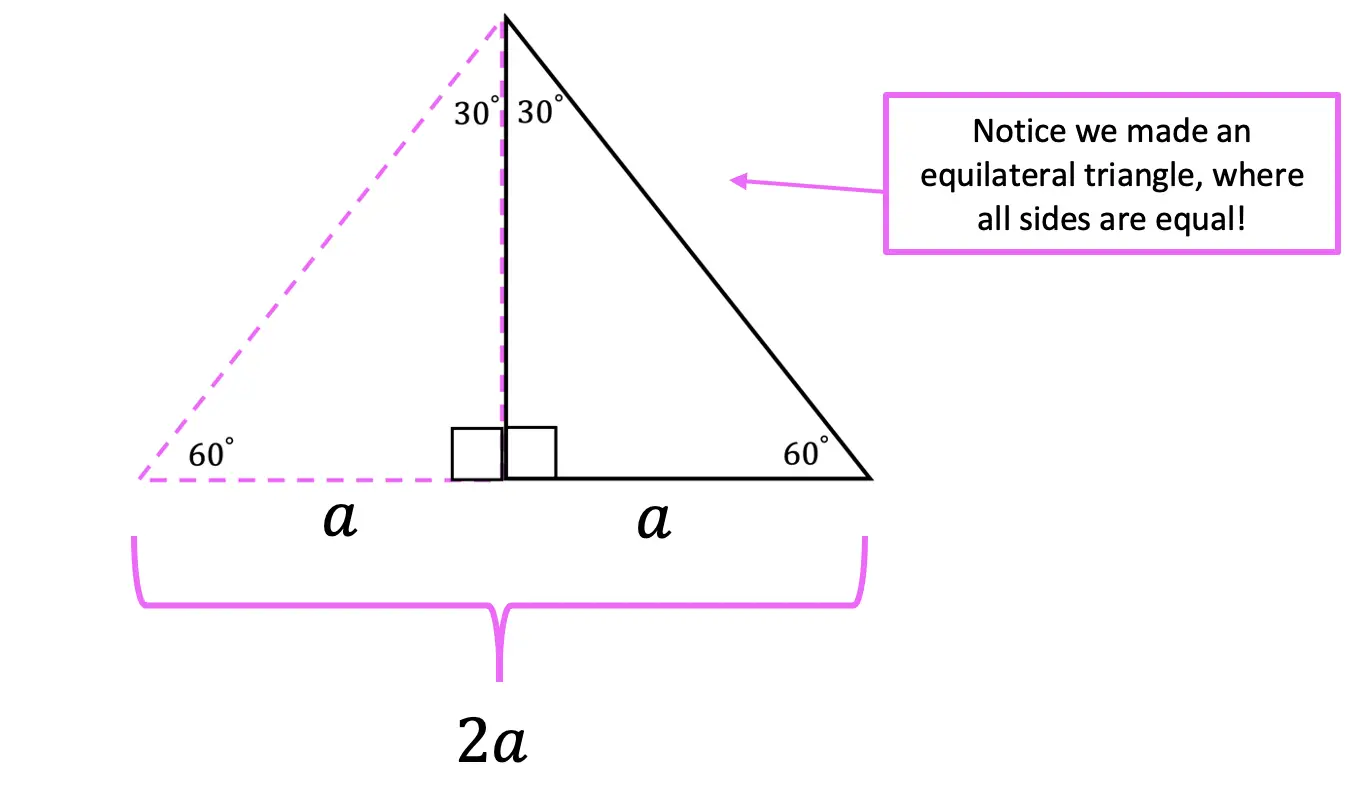
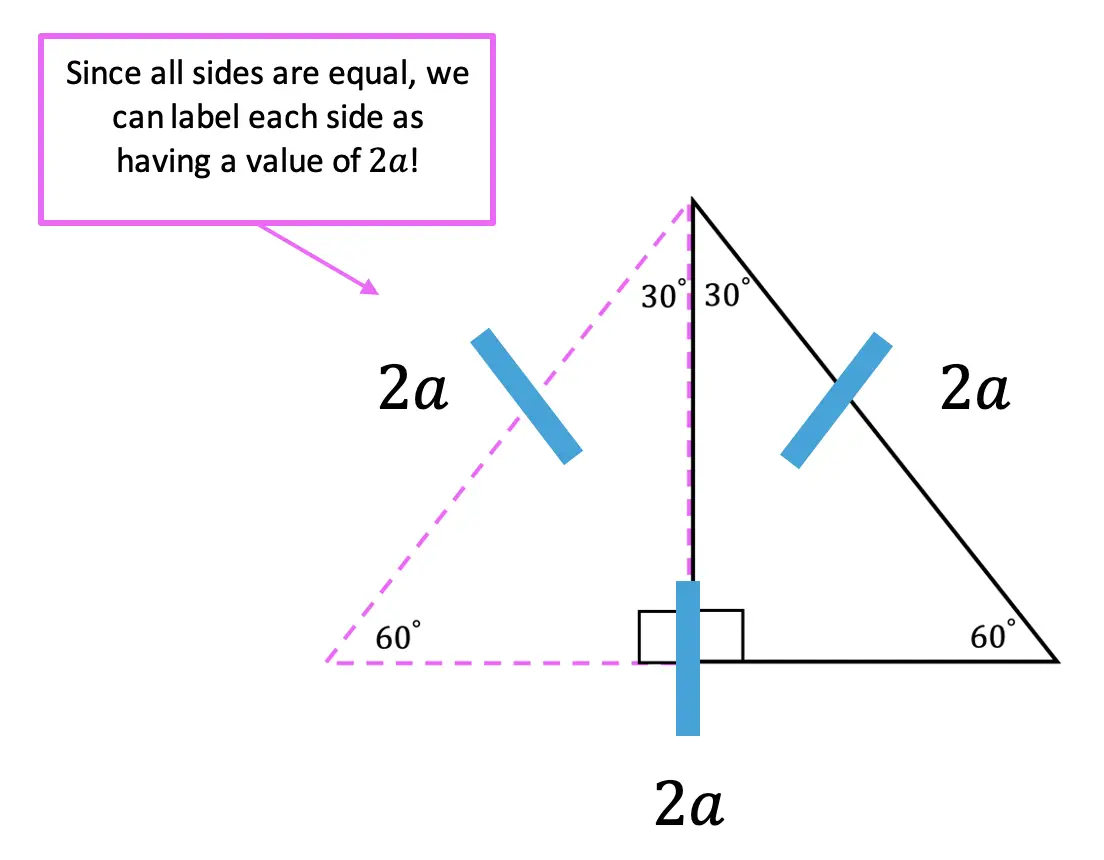
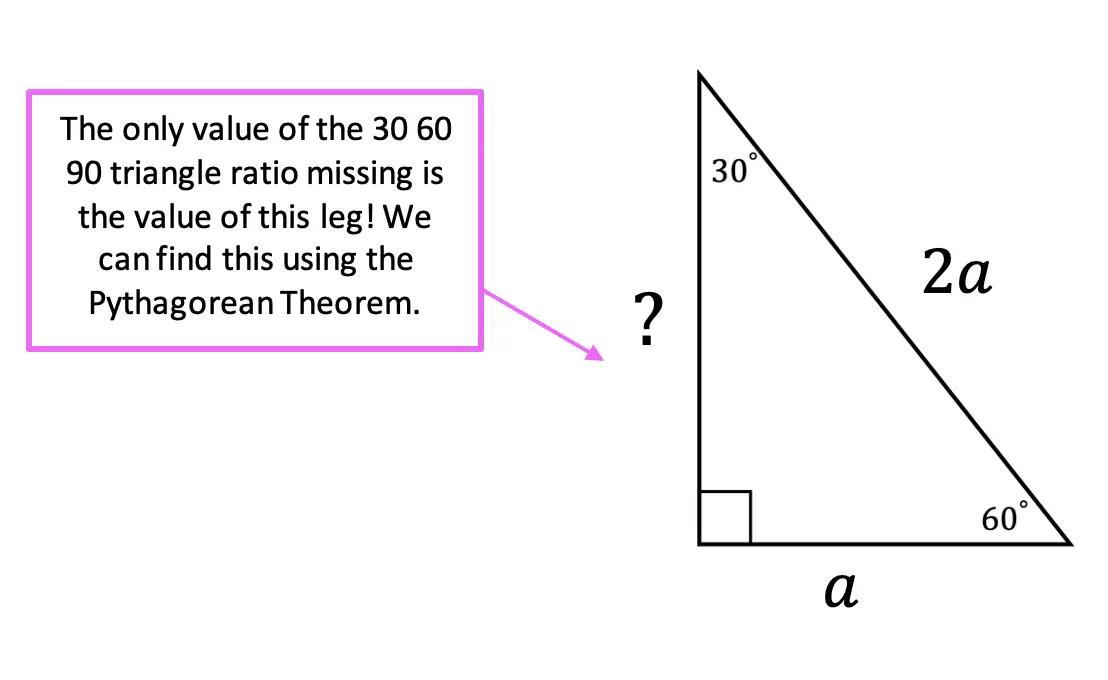
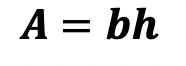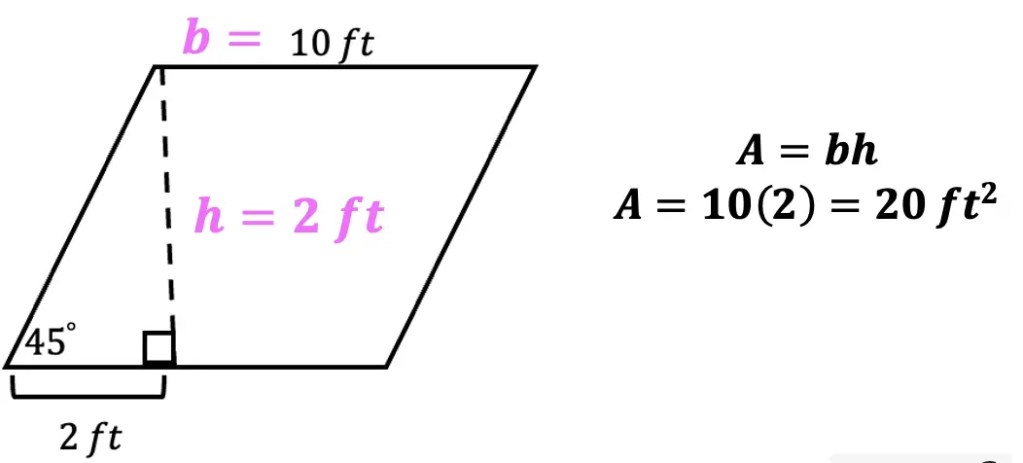Greetings! We are going to do something a little different today and explore Math + Art: Math Behind Perspective Drawing. For all the artists out there who tend to not generally gravitate towards math, this post is for you! There are many ways math can be connected to art, and in this post we will explore the role parallel and perpendicular lines play when it comes to drawing 3-D shapes. And for those who want to learn even more, don’t forget to check out the video below to see how 2-point perspective applies geometry and angles to create 3-D shapes.
What is Perspective Drawing?
Perspective drawing is an art technique that allows us to draw real life objects in 3-D on a flat piece of paper. Notice in the example below that buildings, trees, and power lines get smaller and smaller as we look into the distance just as they would in real life.

What are the Basics of Perspective Drawing?
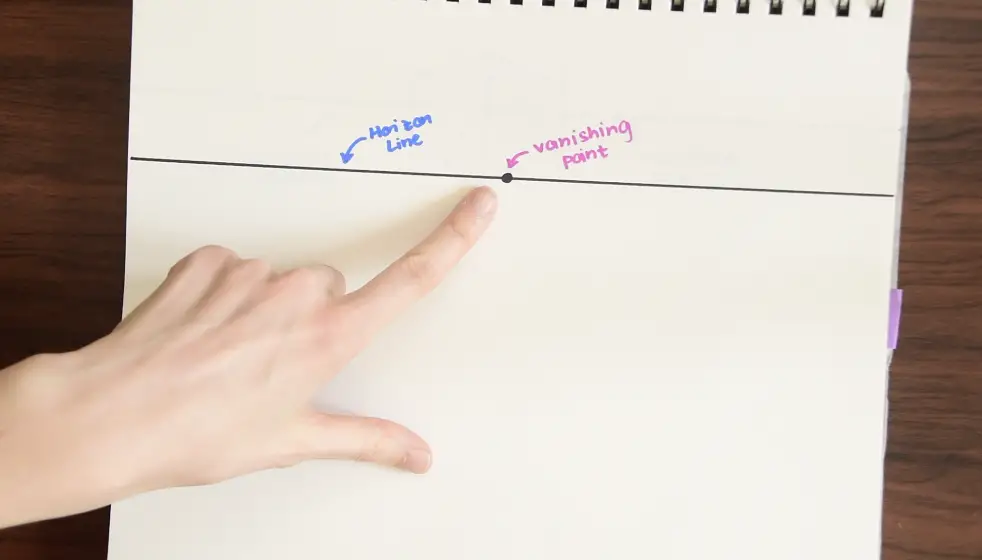
There are two main things we need to know about perspective drawing.
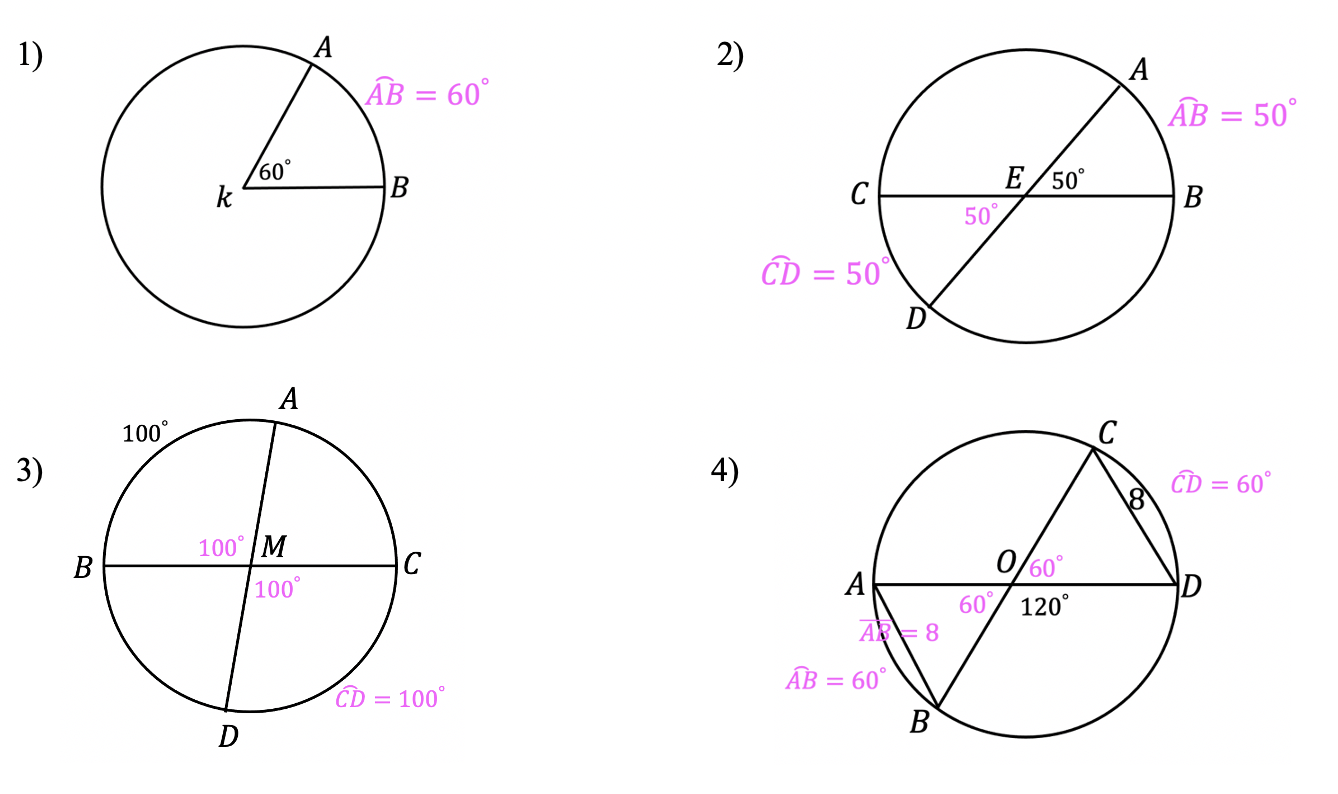
1- Horizon Line: A horizontal line that goes across the entire paper. This represents where land and sky meet.
2- Vanishing Point: This is where many of our lines will be directed in order to create that 3-D affect.
Where do I Begin?
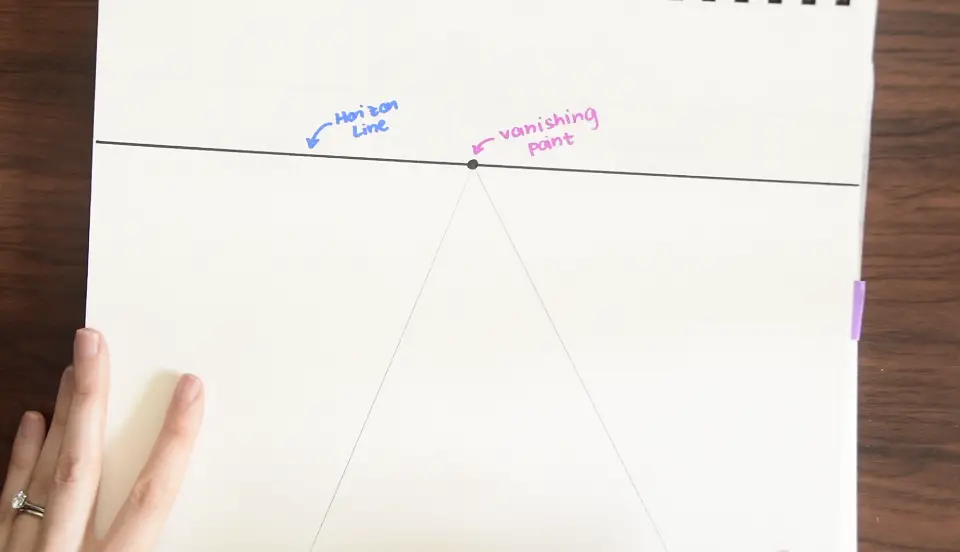
Step 1- Now that we have our horizon line and vanishing point, we can start by drawing a road. Use a ruler to draw two lines that lead to the vanishing point, this should resemble a triangle.
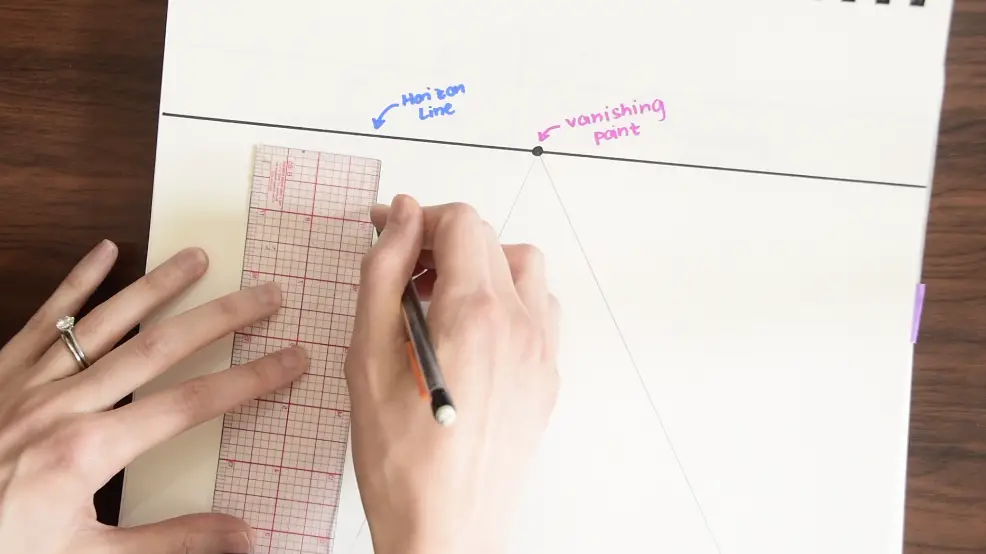
Step 2-From here we can start to draw a building by creating two straight lines that are perpendicular to our horizon line.
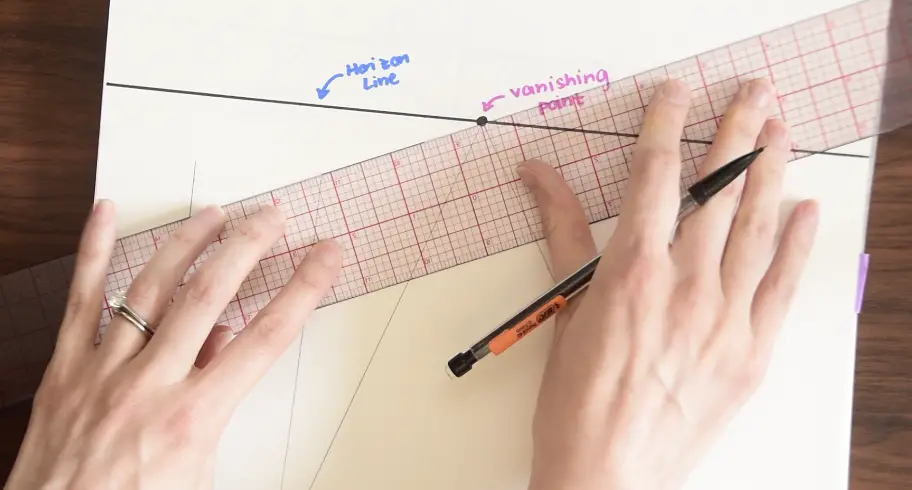
Step 3-Then line up the outermost corner of the building with the vanishing point using a ruler, and draw a line. Do this with each corner of our rectangle for a 3-D effect.
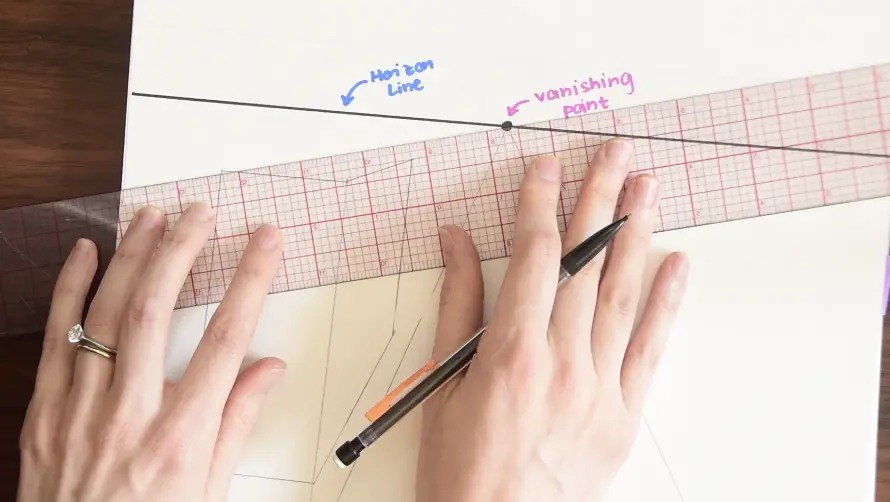
Step 3- continued….
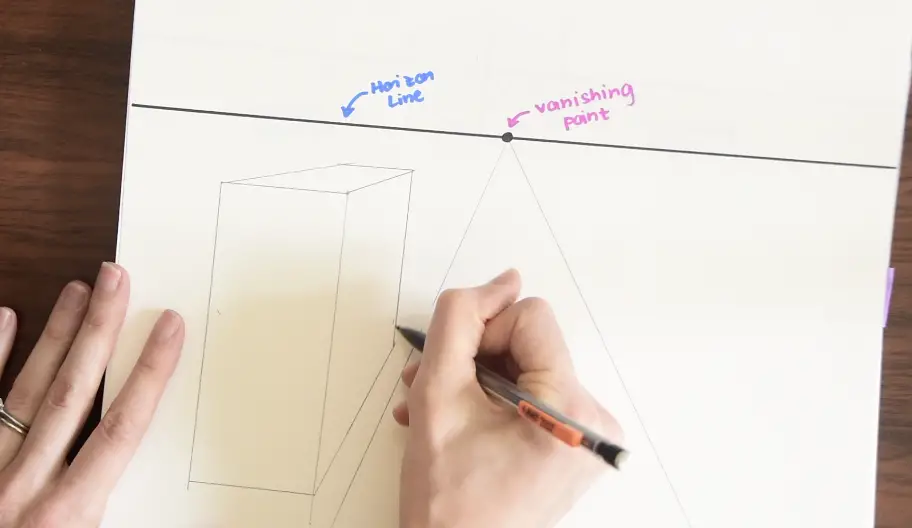
Step 4- For the remaining lines, use parallel and perpendicular lines to finish off our building.
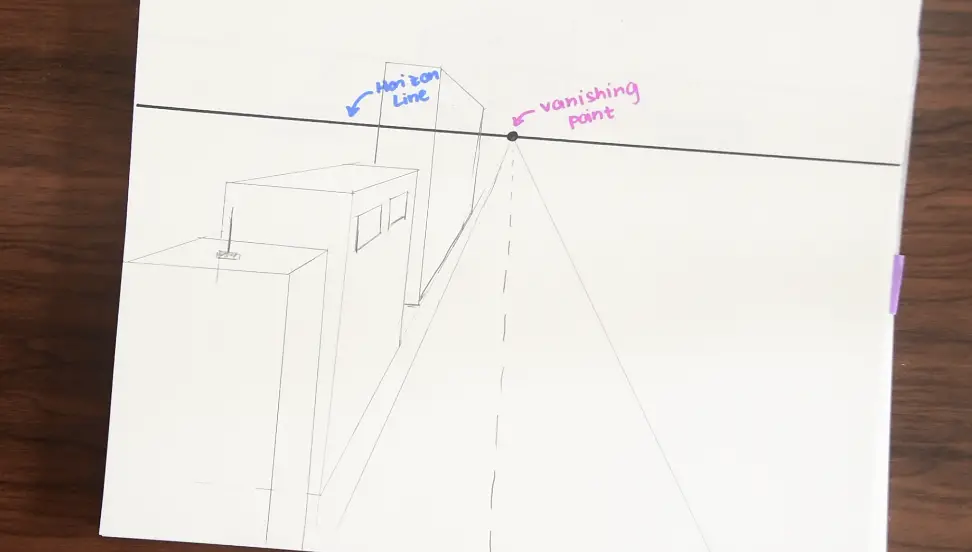
Step 5- Get creative! Add more buildings, windows, antennas, and anything else you might see in a city -scape. Use your imagination! 🙂
This method of perspective drawing is called one-point perspective because there is one vanishing point. But there are also 2-point and 3-point perspectives we can draw!
Want to learn how to do 2-Point Perspective drawing with 2 vanishing points!? Check out the video above to see how geometry and angles are related to this technique of perspective drawing!
Still got questions or want to learn more about perspective drawing? No problem! Don’t hesitate to comment with any questions below. Thanks for stopping by and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
For more math + art, check out this post on fractals found in nature here.