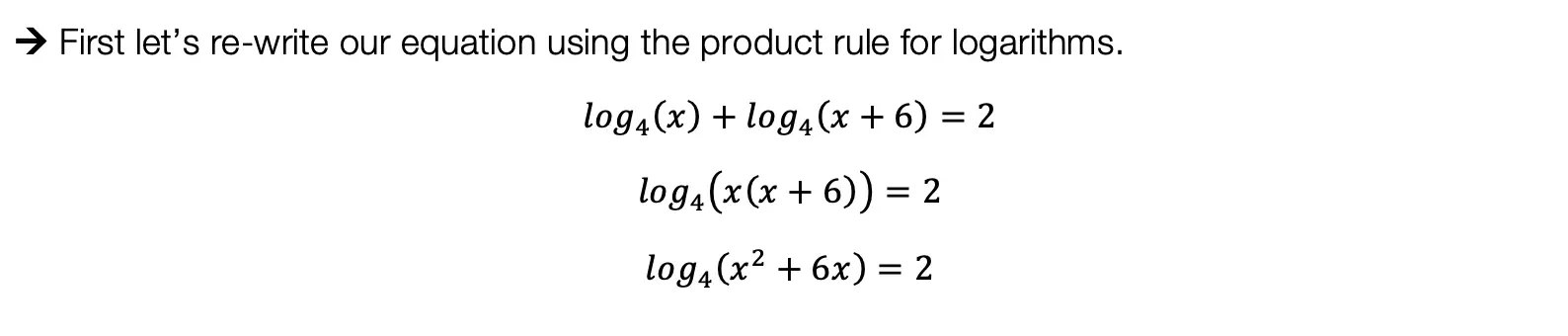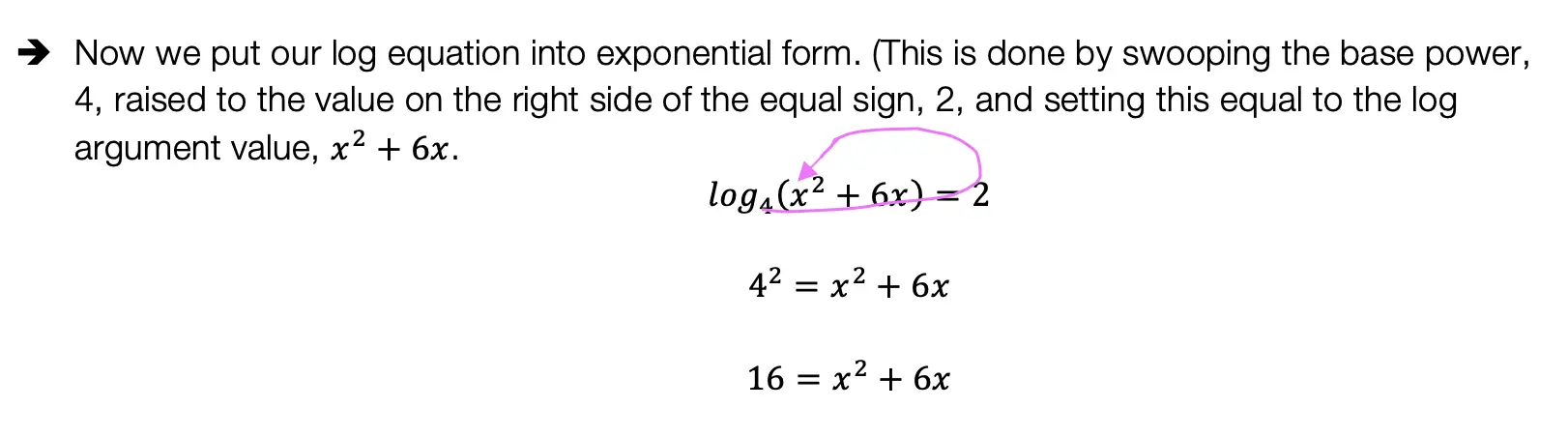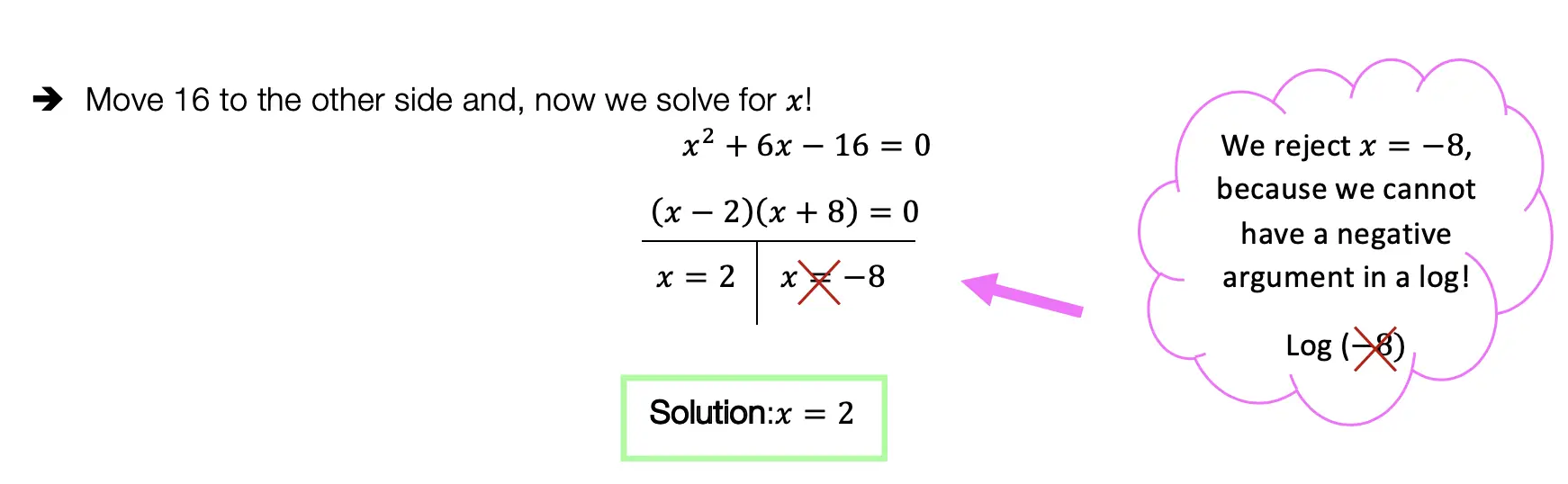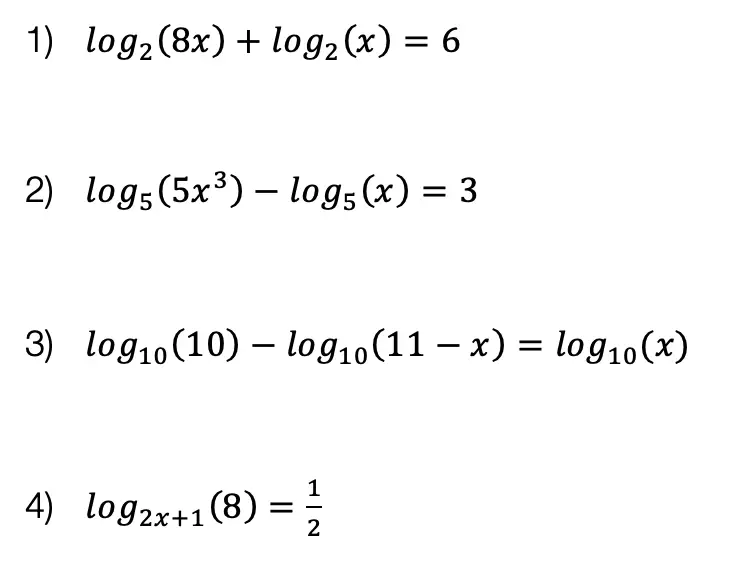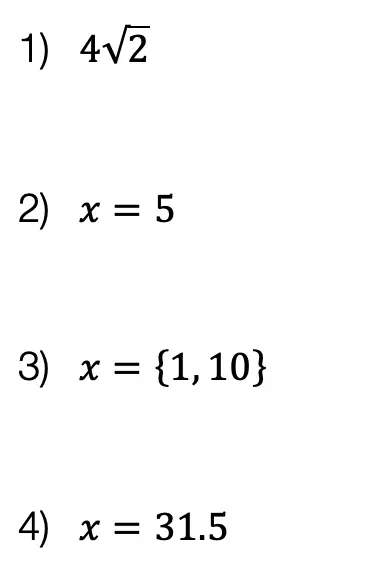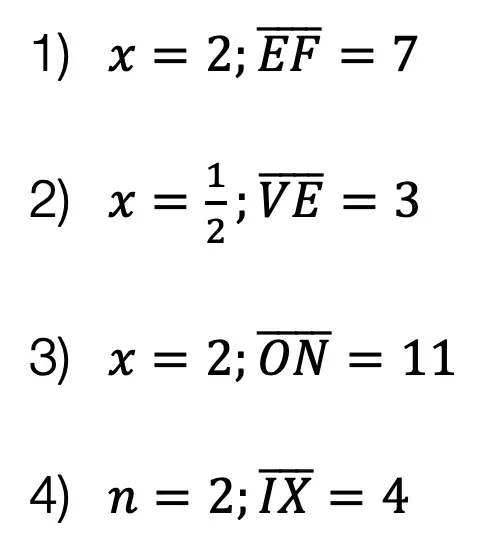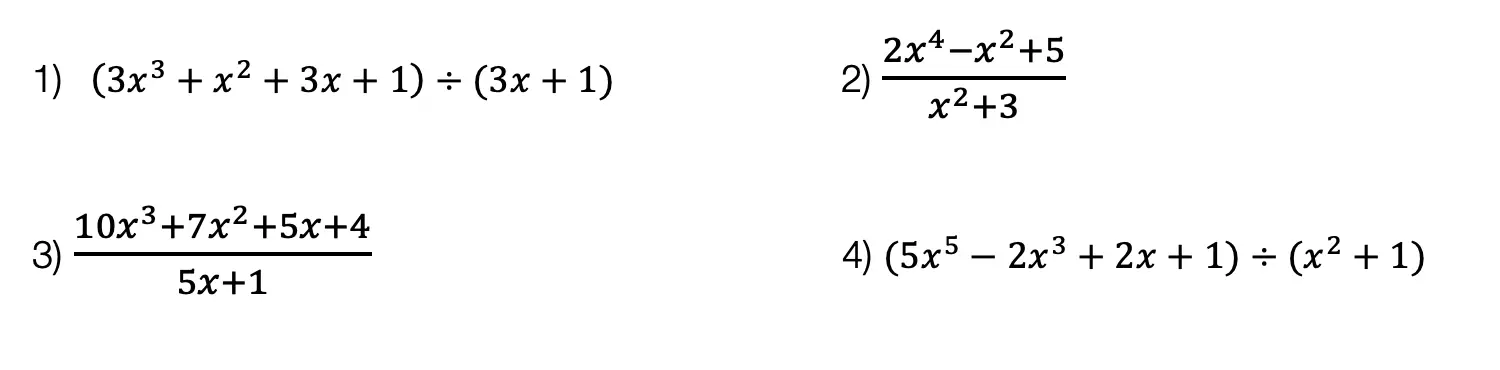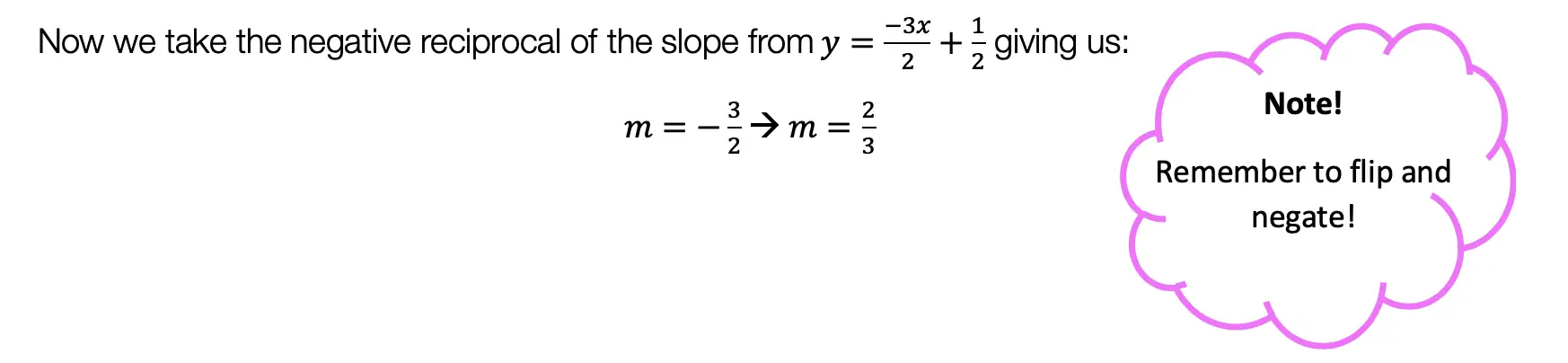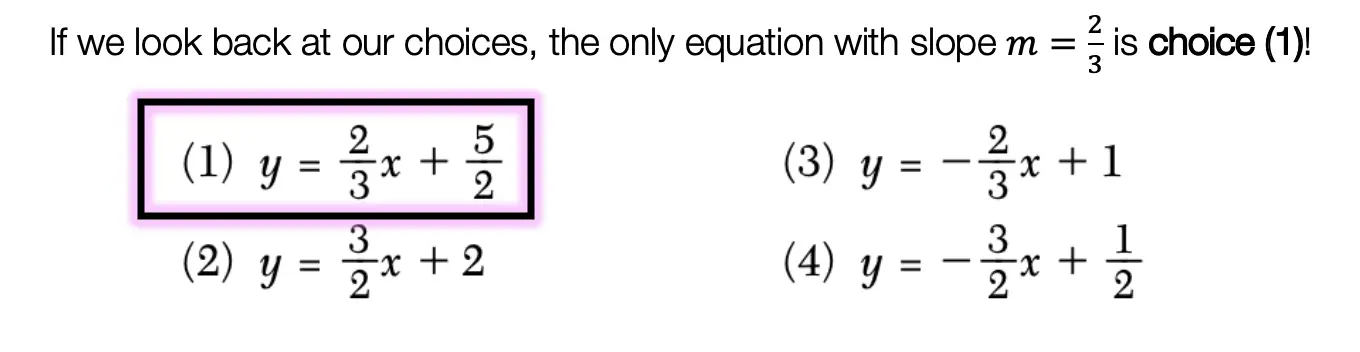Greeting math friends and welcome to Mathsux! In this post, we are going to start with the very basics of trigonometry by going over how to find a missing angle and/or side length of right triangles while using the famous trigonometric function sine, cosine, or tangent, (aka how to use SOH CAH TOA). Woo hoo! These are the basics of right triangle trigonometry, and provide the base for mastering so many more interesting things to come in trigonometry! So, let’s get to it!
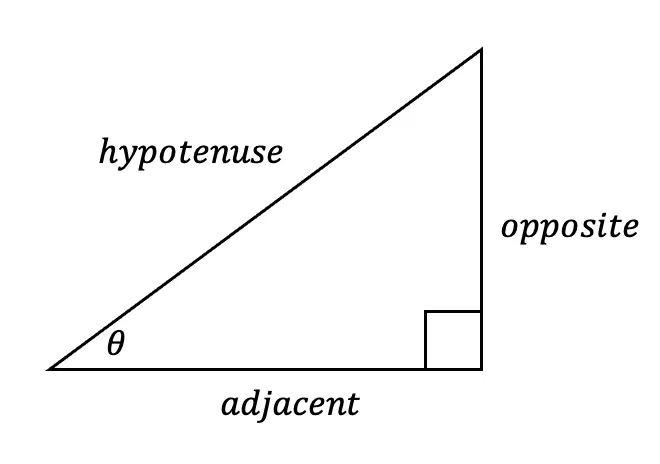
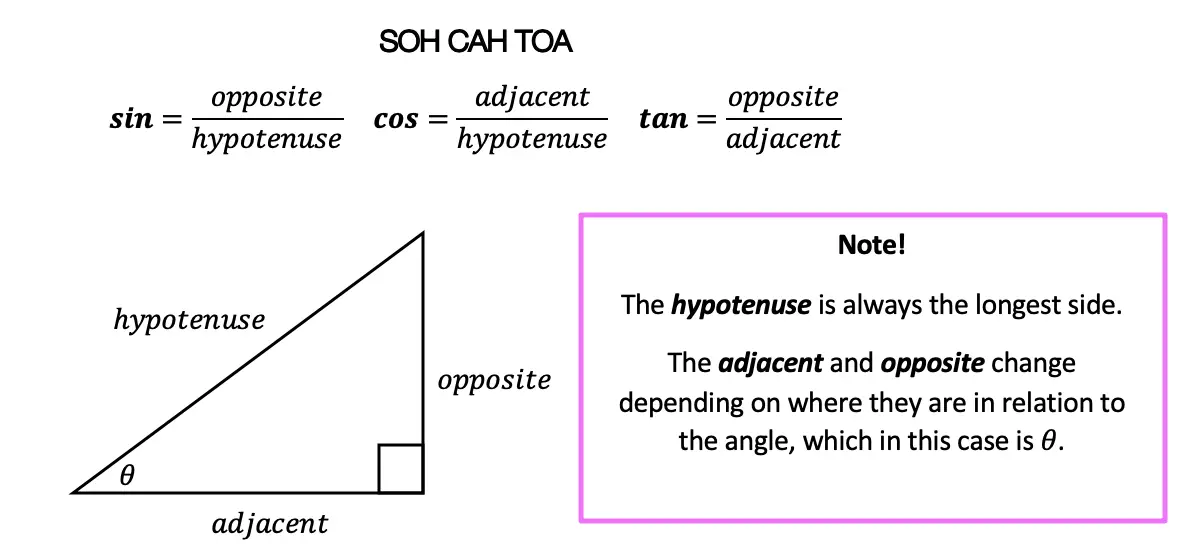
SOH CAH TOA is an acronym that stands for the following trig functions and parts of a right triangle. We’ll explain more in this post!
SOH CAH TOA
| Sin = Opposite/Hypotenuse | Cosine= Adjacent/Hypotenuse | Tangent= Opposite/Adjacent |
Also, if you have any questions about anything here, don’t hesitate to comment below or watch the video below. Also, don’t forget to subscribe to MathSux for FREE math videos, lessons, and practice questions every week. Happy calculating! 🙂
What does SOH CAH TOA stand for?
A Trigonometric Ratio, more commonly known as Sine, Cosine, and Tangent, are trig ratios that naturally exist within a right triangle. This means that the sides and angles of a right triangle are in proportion within itself. It also means that if we are missing a side or an angle of a right triangle, based on what we’re given, we can figure out what the value of the sides or angles are, based on these ratios!
Let’s take a look at what Sine, Cosine, and Tangent are all about!
Ready for your first right angled triangle example? Check it out below!
SOH CAH TOA Example #1:
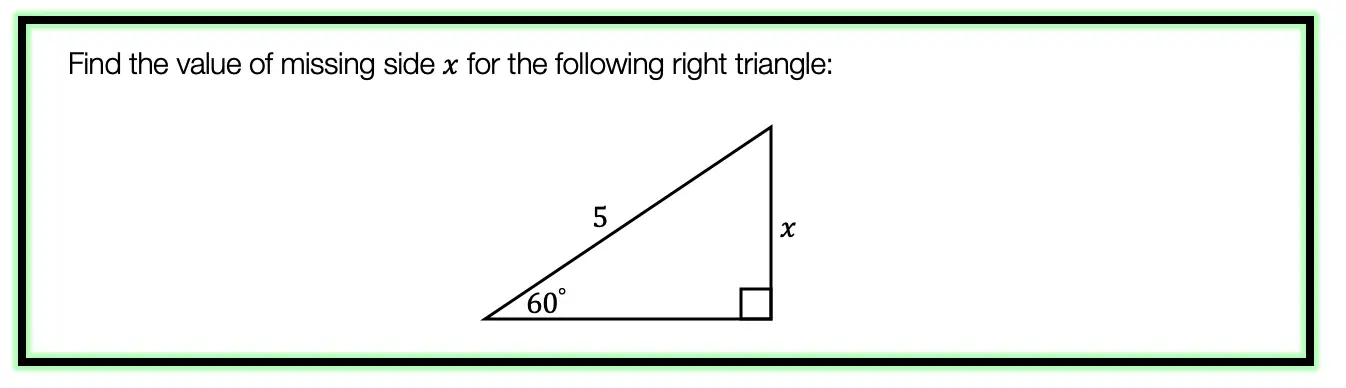
Now let’s see how we can apply trig ratios when there is a missing side or angle in a right triangle!
Step 1: First, let’s identify the different sides of our right triangle depending on which angle we are focusing on, which in this case is a 60º angle. Based on the locations of our angle, we can label each side as the hypotenuse, adjacent, or the opposite.
Notice below, that the opposite side labeled x, is labeled the “opposite” side because it is opposite to our given angle, 60º. The remaining side is considered the adjacent side of our triangle because it is directly next to our given angle, 60º.
Step 2: Now, let’s write out SOH CAH TOA. Notice the only trig function that uses both the hypotenuse and the opposite is sine! Knowing to use the sine function, let’s fill in our formula using the hypotenuse = 5 and opposite = x in order to find the value for missing side length x.
In order to use the sin function correctly, we’re going to need to plug in our given angle, which is 60º, and then set up our proportion. sin(60º)=x/5. By using the sine function, our calculator, and a little bit of algebra we’ll be able to solve for the unknown side.
Ready for another example?! Check out another SOH CAH TOA problem using right triangles below!
Right Triangle Trig Example #2:
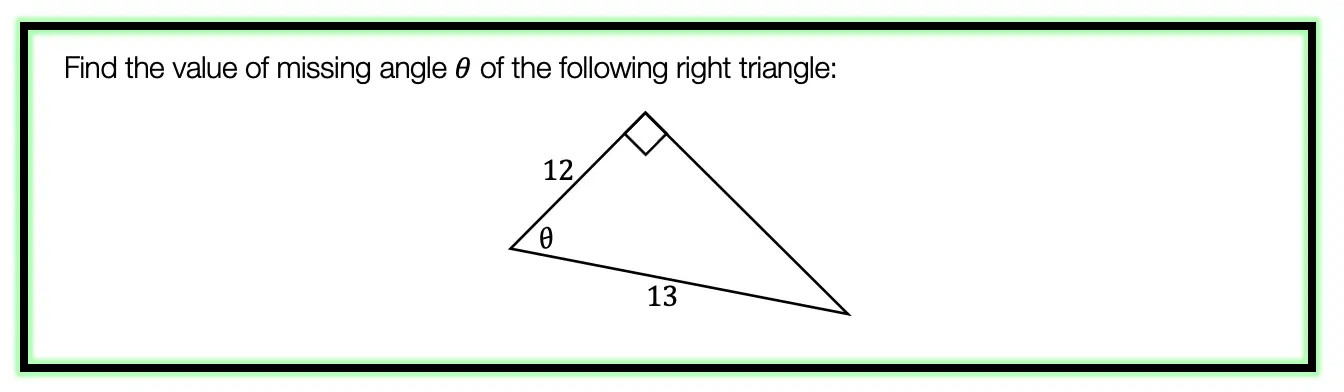
Step 1: First, let’s identify the different parts of the right triangle we are given (the hypotenuse, adjacent, and the opposite). Notice in this example, we are given the adjacent and hypotenuse and need to find the value of the unknown angle, θ.
Step 2: Next, let’s write out our acronym, SOH CAH TOA, to see which trig function can help us with our question! Notice the only trig function that uses both adjacent and hypotenuse is cosine. This is what we will use to solve for the unknown angle, θ.
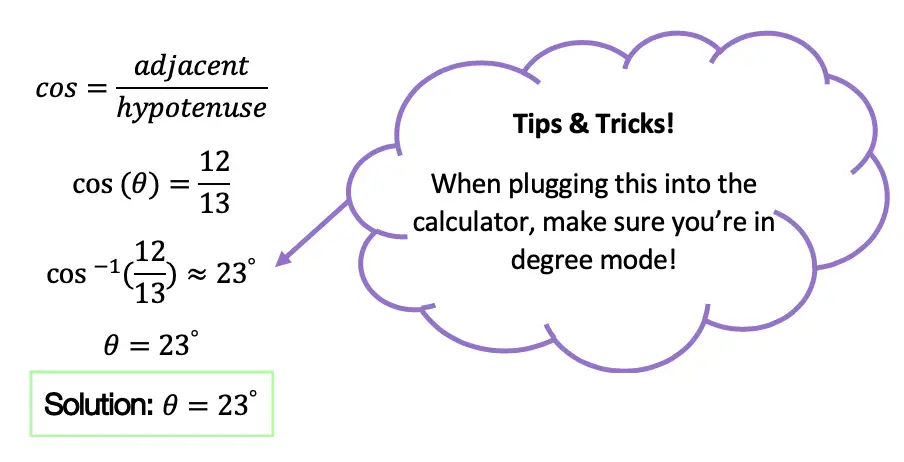
We use cosine, by setting up our proportion, cos(θ)=adjacent/ hypotenuse, knowing we can then plug in 12 for our adjacent value, and 13 for our hypotenuse value.
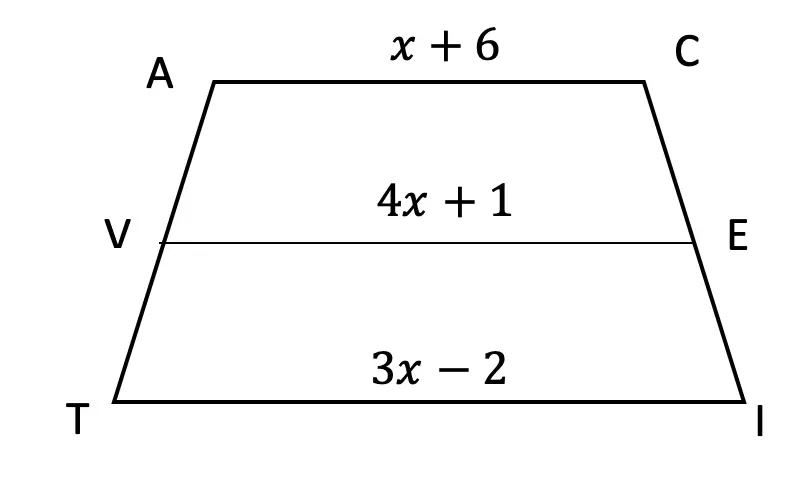
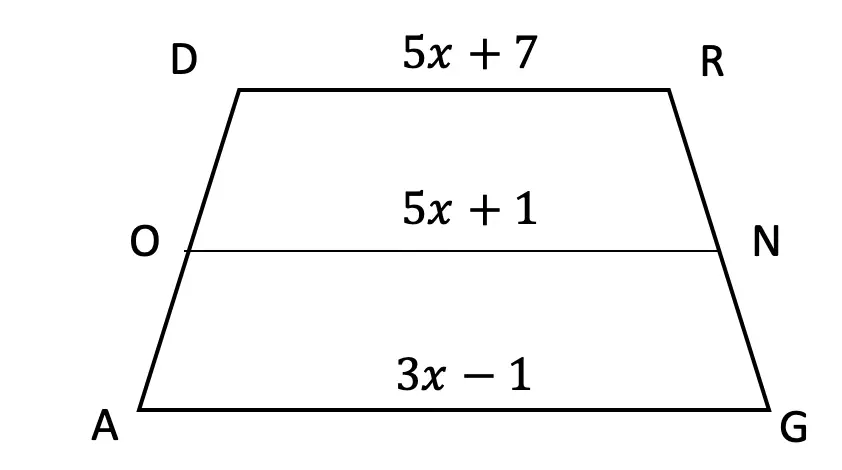
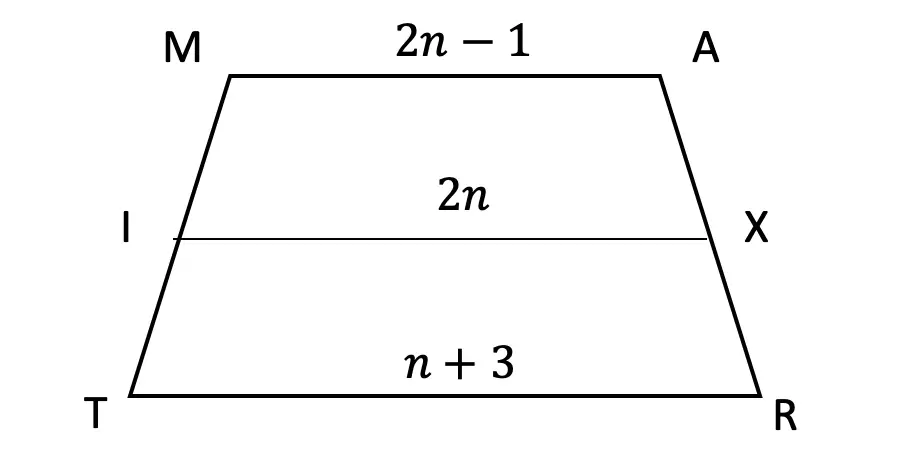
Think you’re ready to test out SOH CAH TOA on your own? Try the following Practice Questions on your own!
Practice Questions:
Given the following right triangles, find the missing lengths and side angles rounding to the nearest whole number.
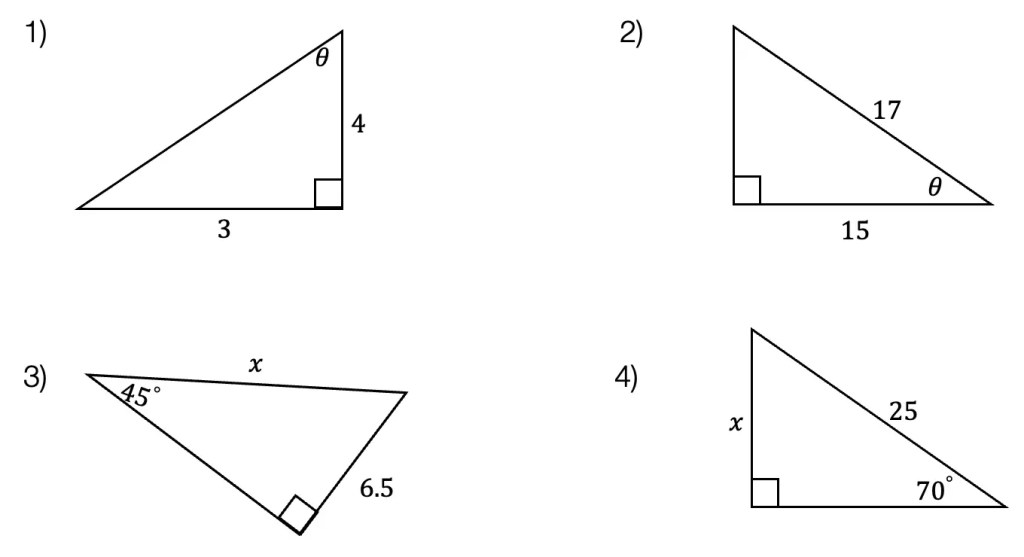
Solutions:
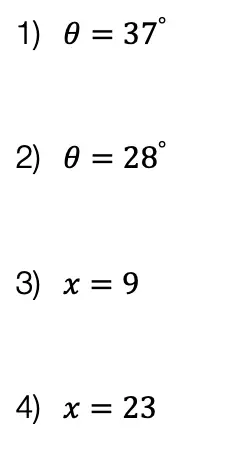
Still got questions? No problem! Check out the video the same examples outlined above and happy calculating! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
). But what if it were to get more complicated? That’s where logs come in! 
median, to find the value of median 
is the median of trapezoid ABCDEF, find the value of the median, given the following:2. 
is the median of trapezoid ACTIVE, find the value of the median, given the following:3.
is the median of trapezoid DRAGON, find the value of the median, given the following:
is the median of trapezoid MATRIX, find the value of the median, given the following:
to our quotient! We just put the remainder over the divisor to represent this extra bit of solution.
, but it is only that, an Example! The exact pattern and exponential equation of the future progress of the virus is unknown! We mathematicians, can only measure what has already occurred and prepare/model for the future. To make the virus spread less rapidly, it is our duty to stay home to slow the rate of this exponentially spreading virus as much as possible.
!
, which is the short-handed way to write “
