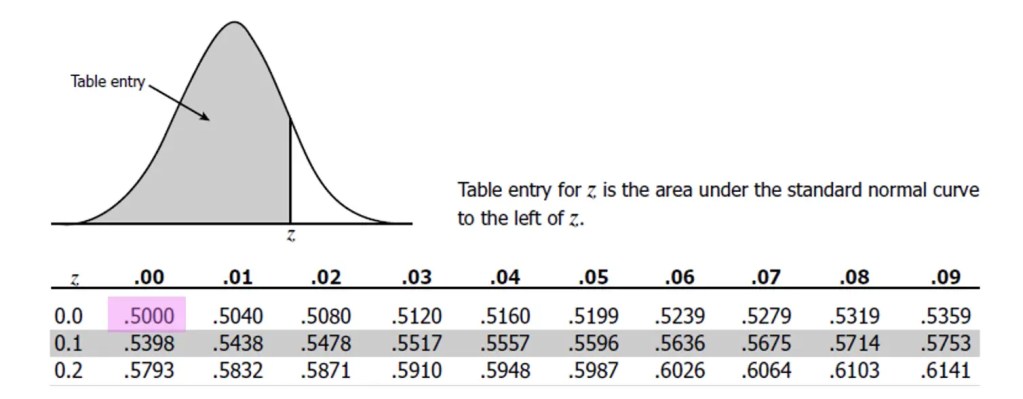
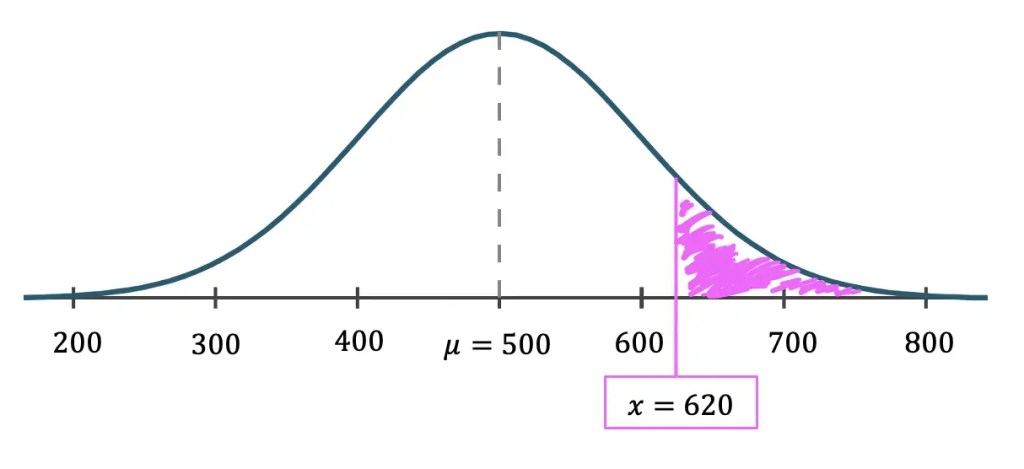
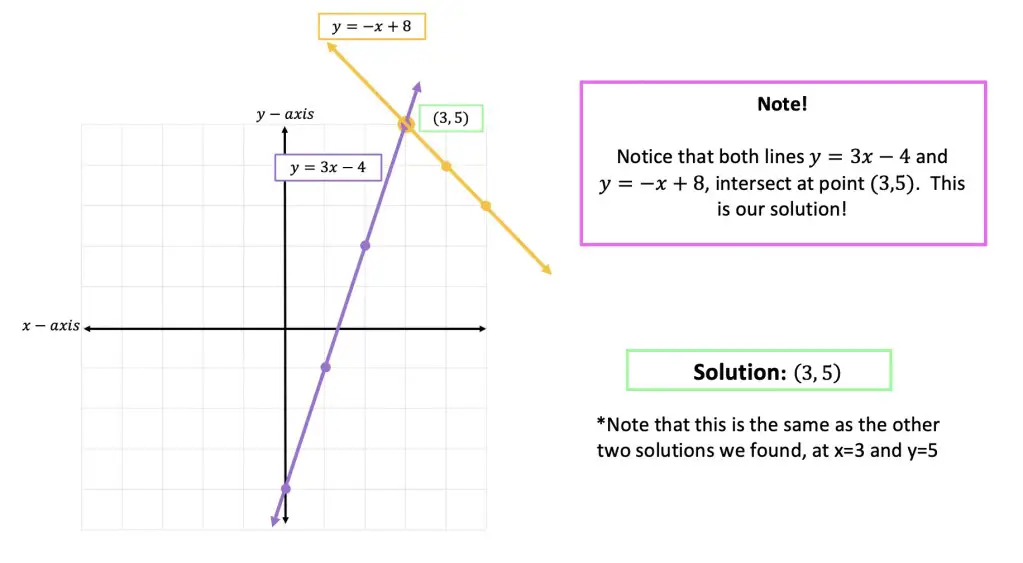
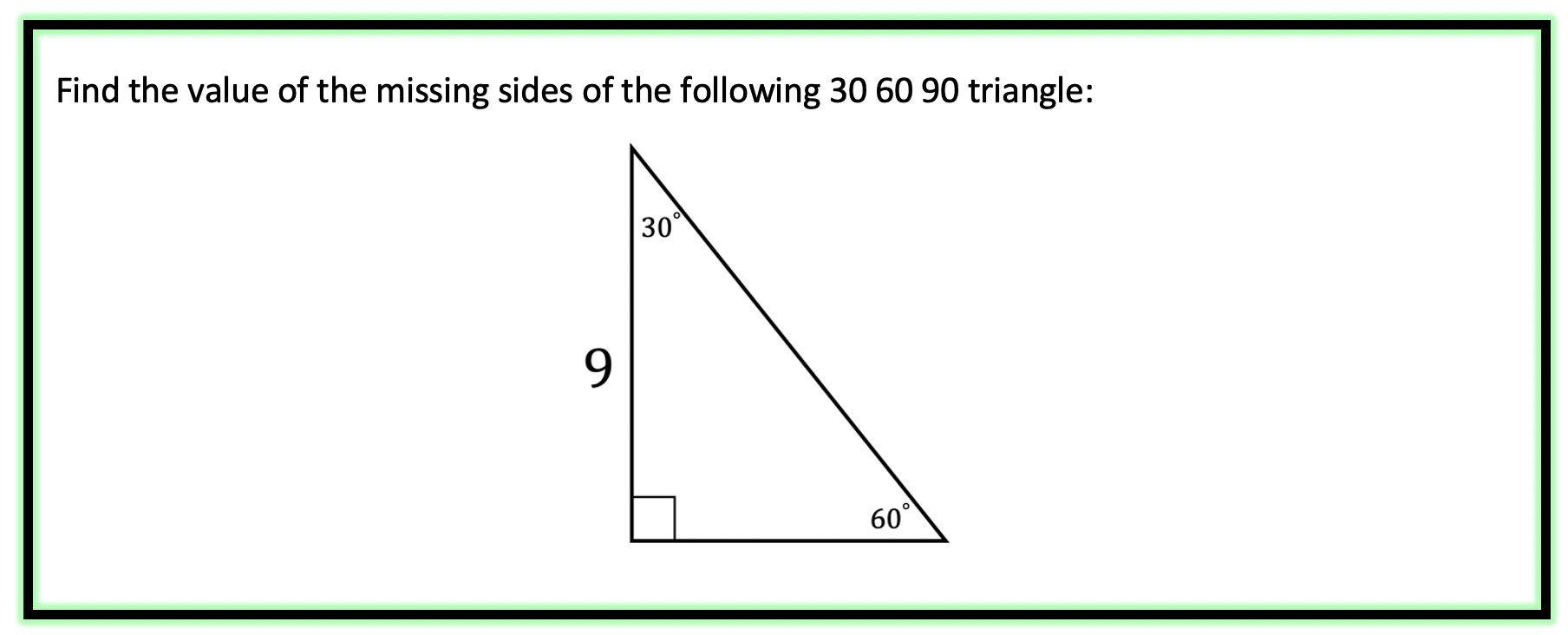
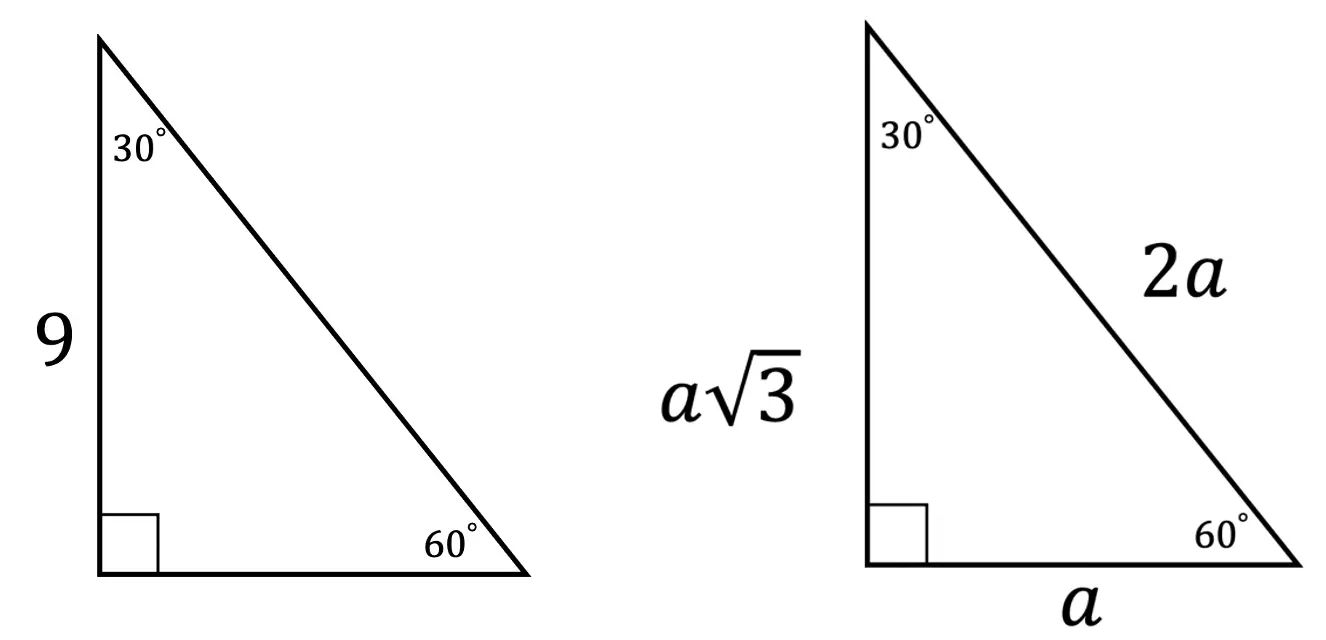
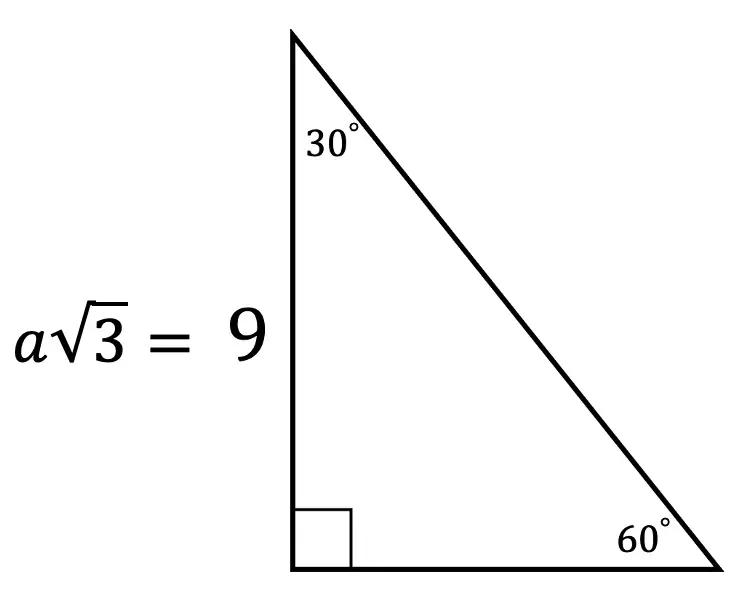
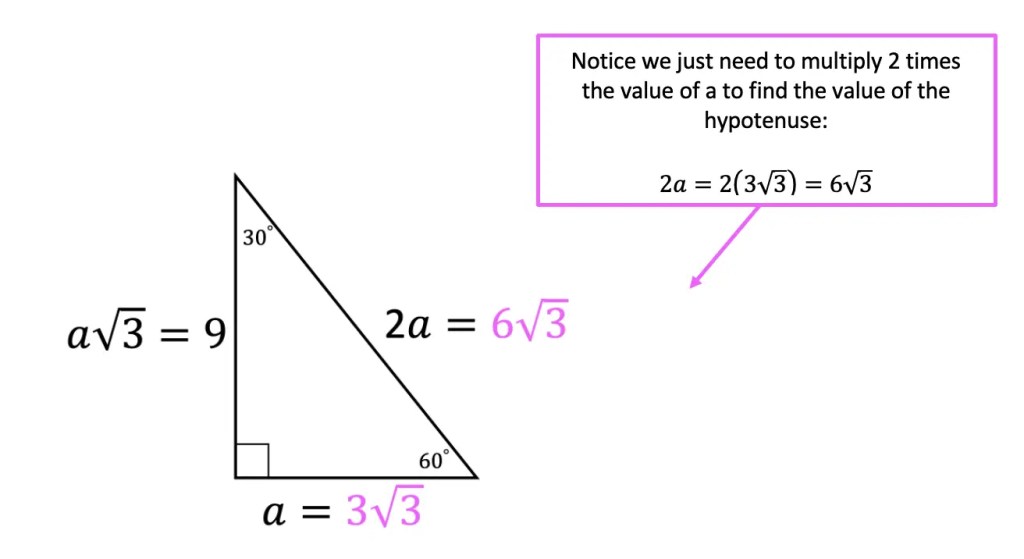
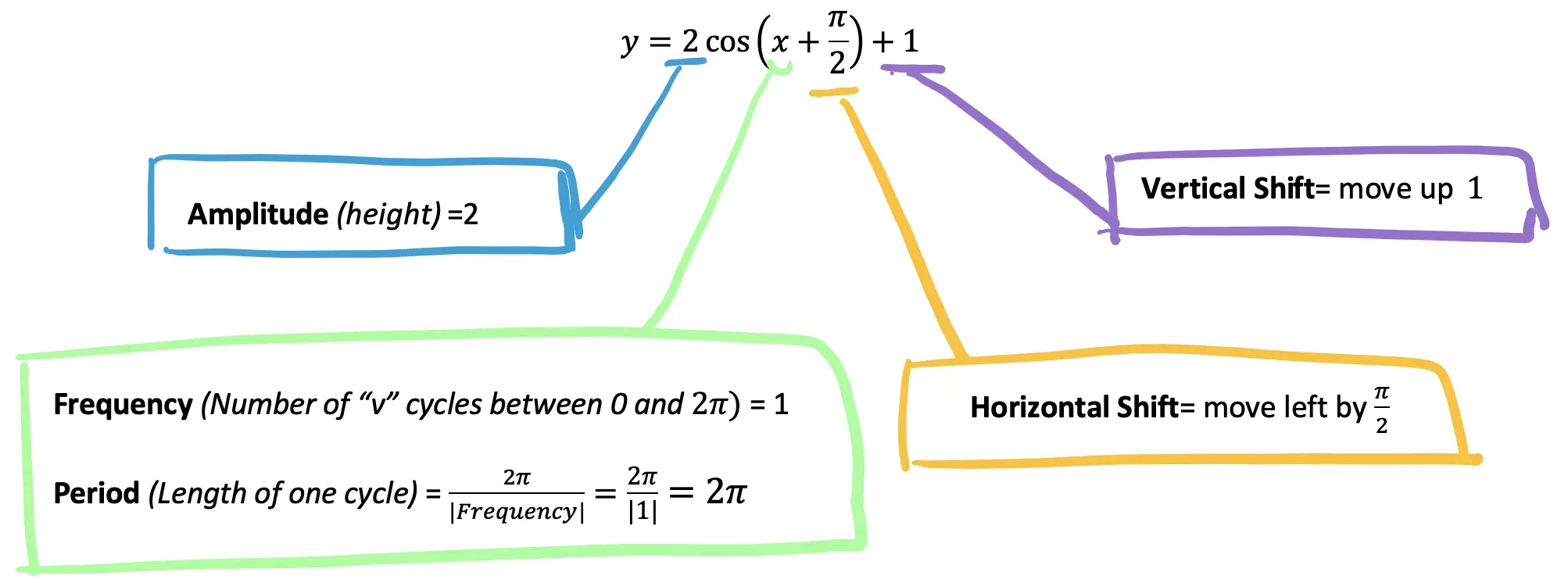
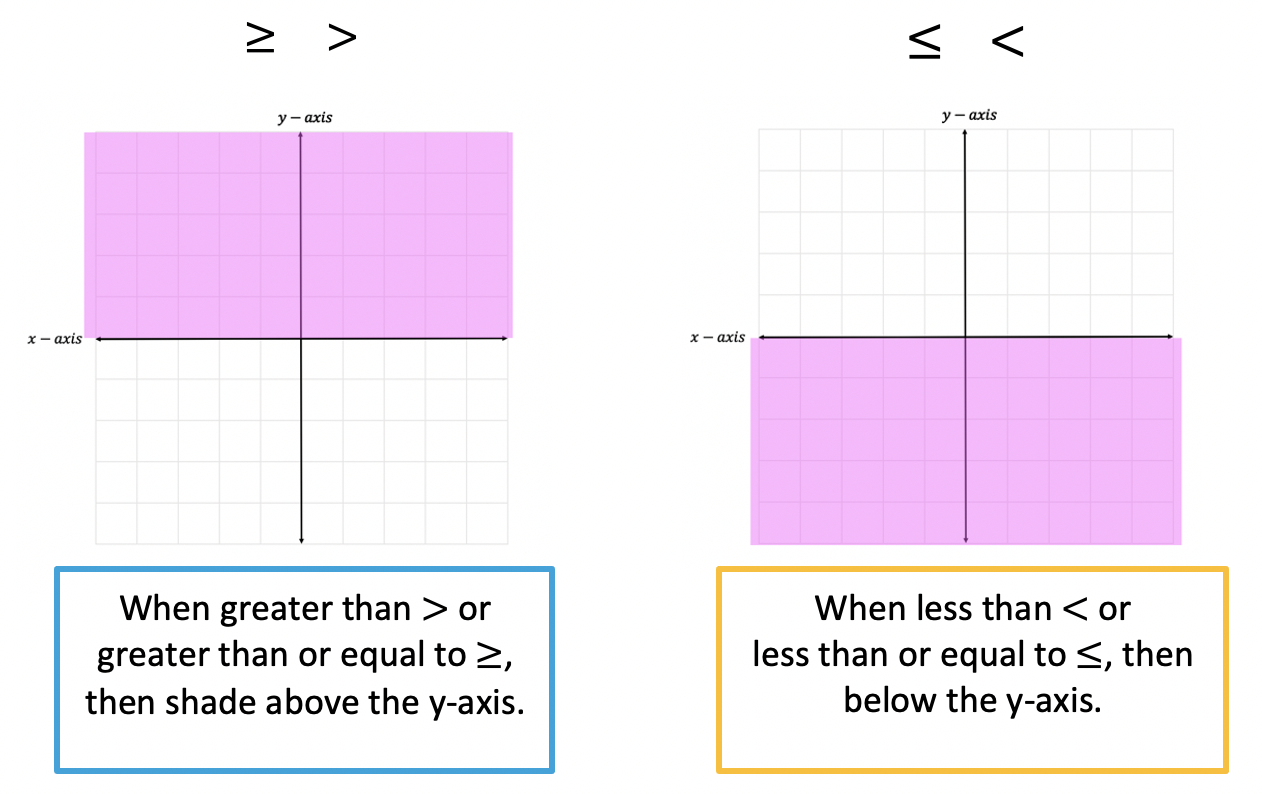
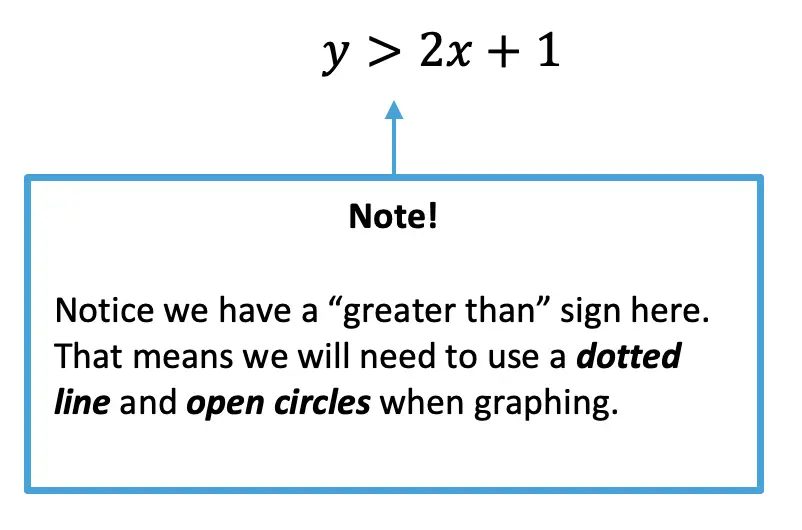
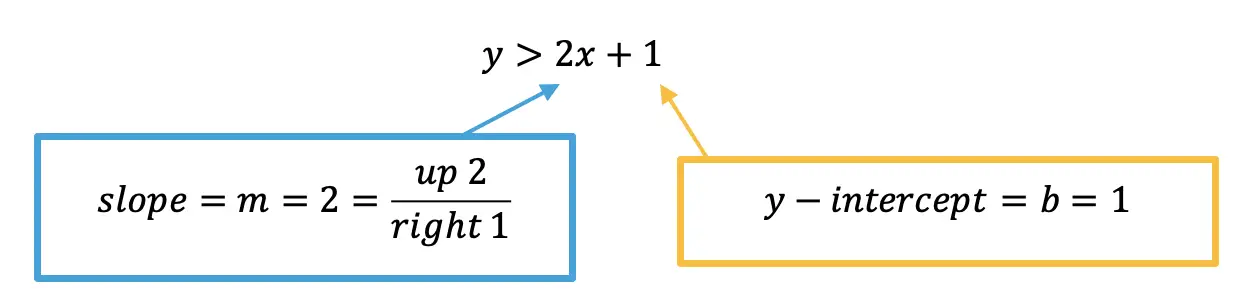
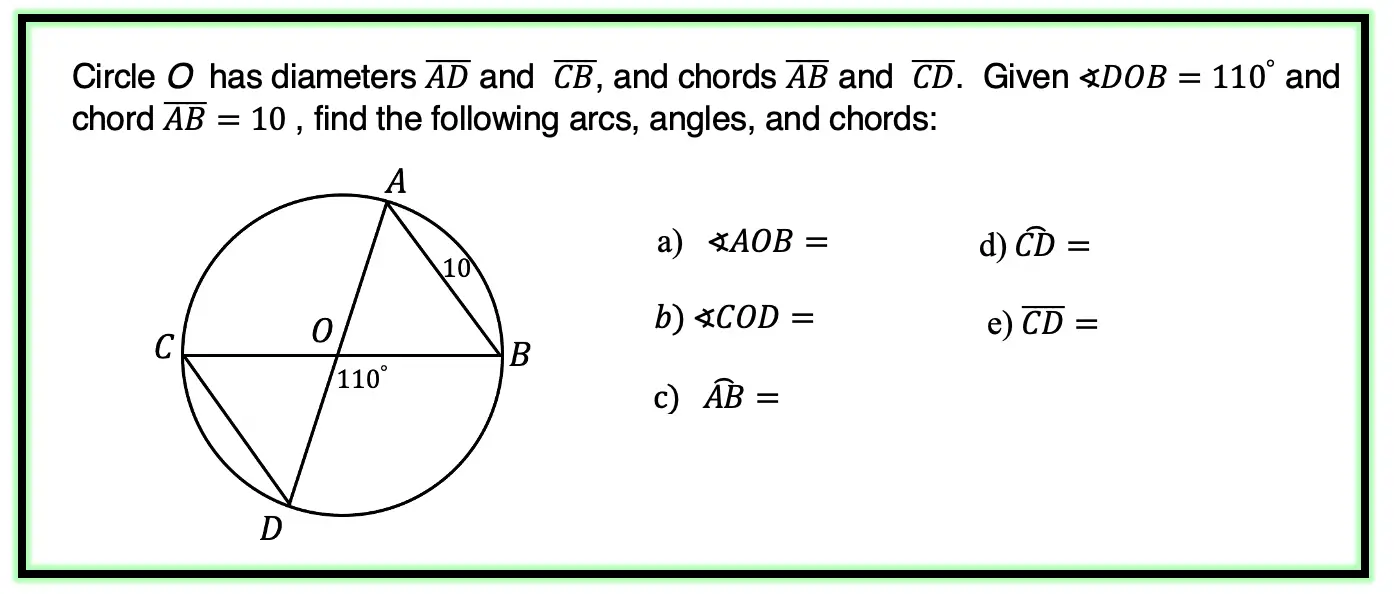
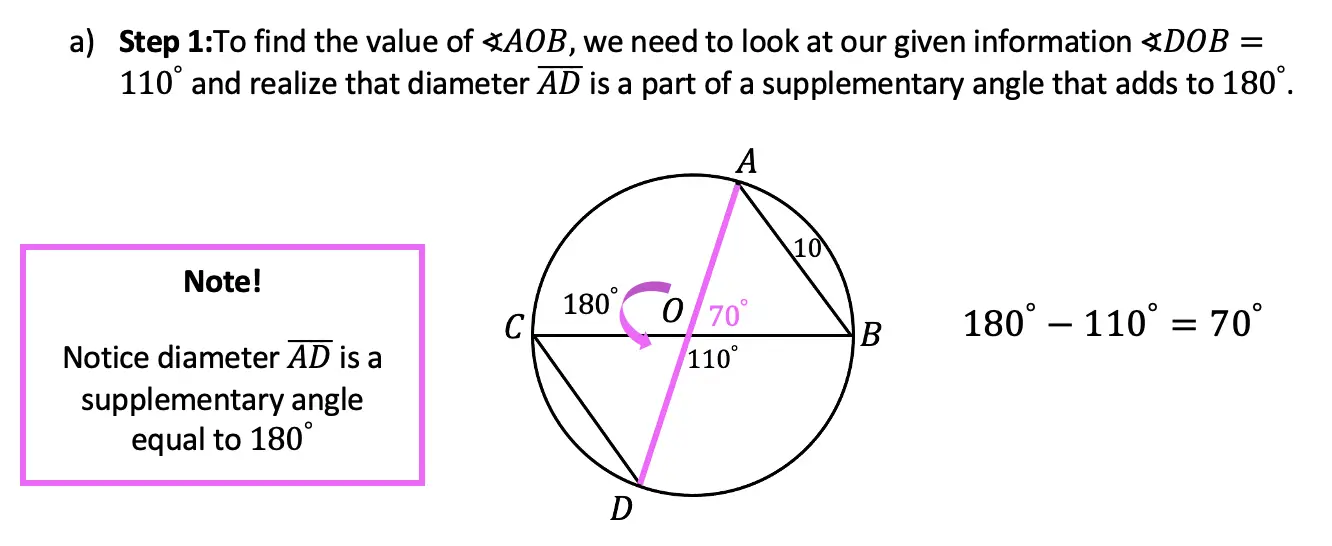
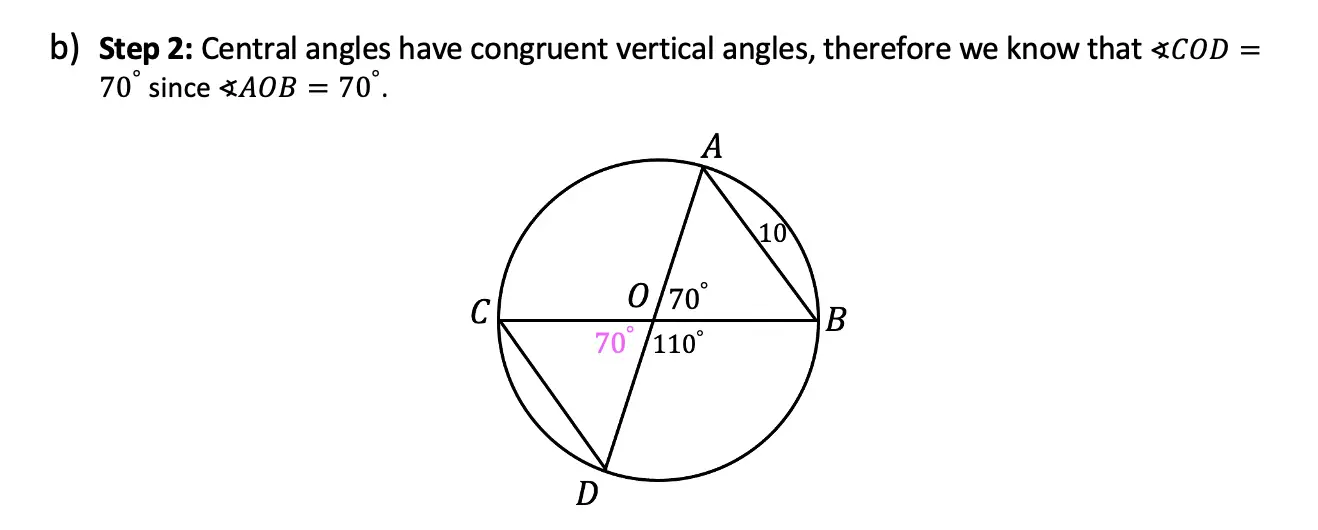
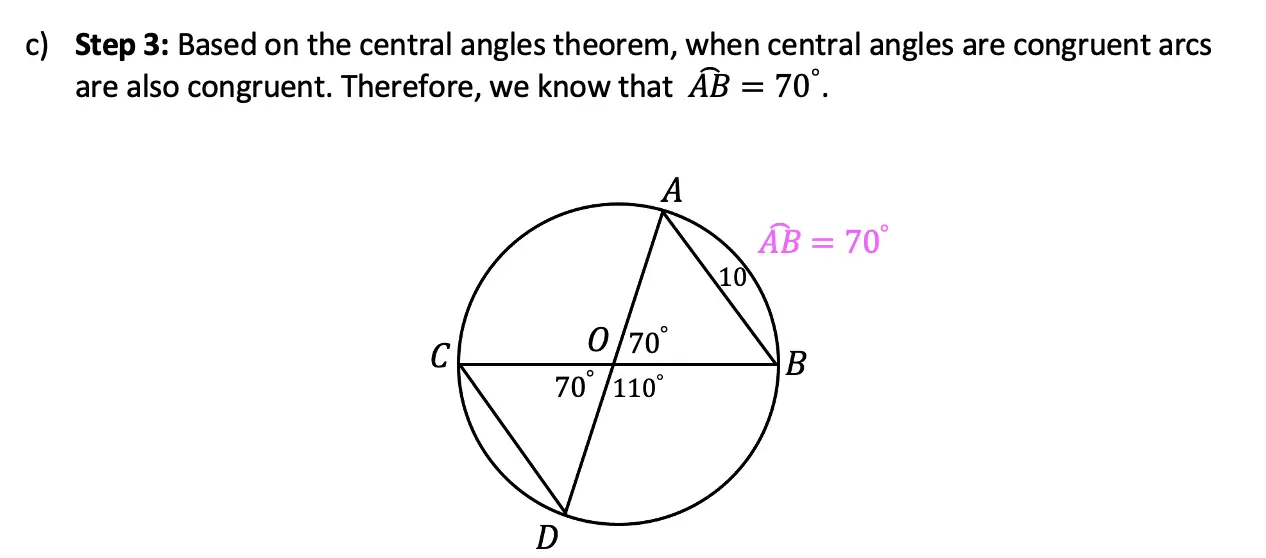
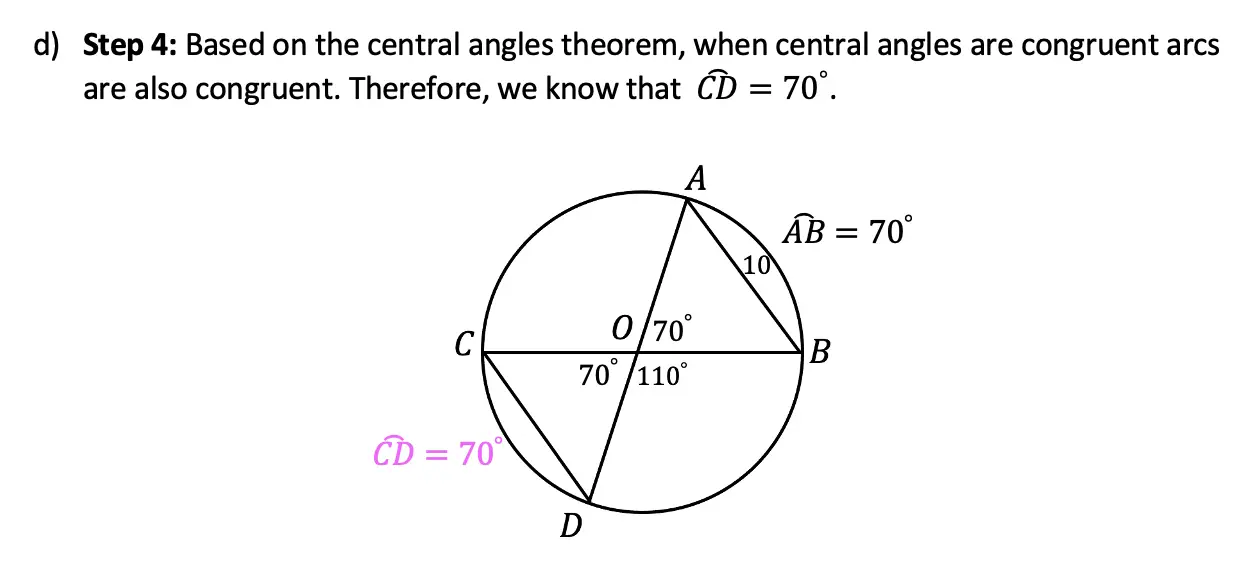
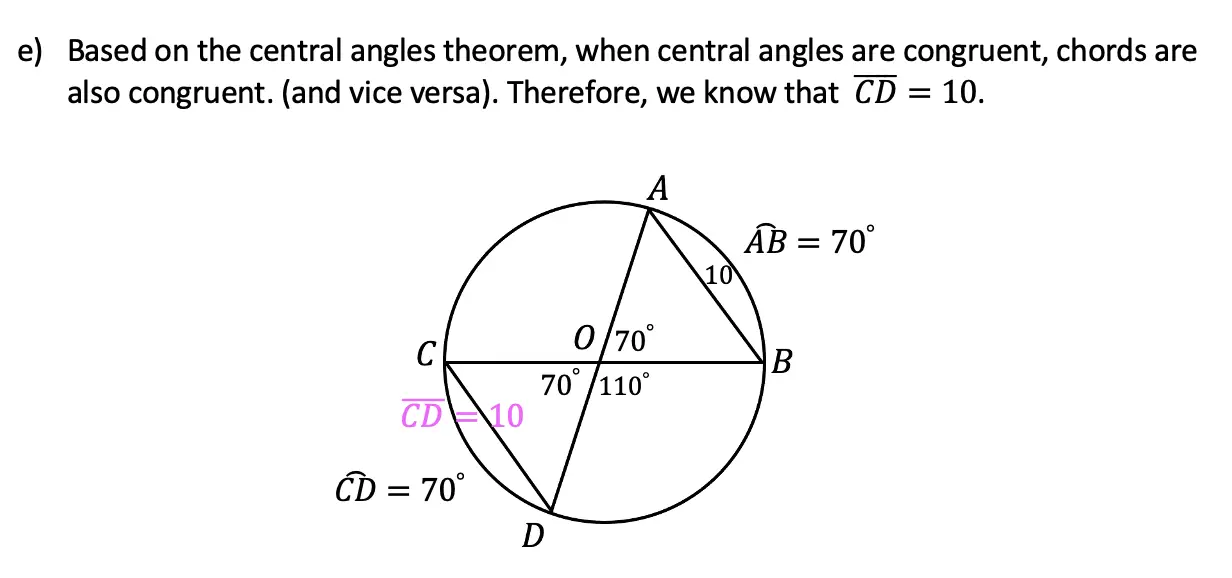
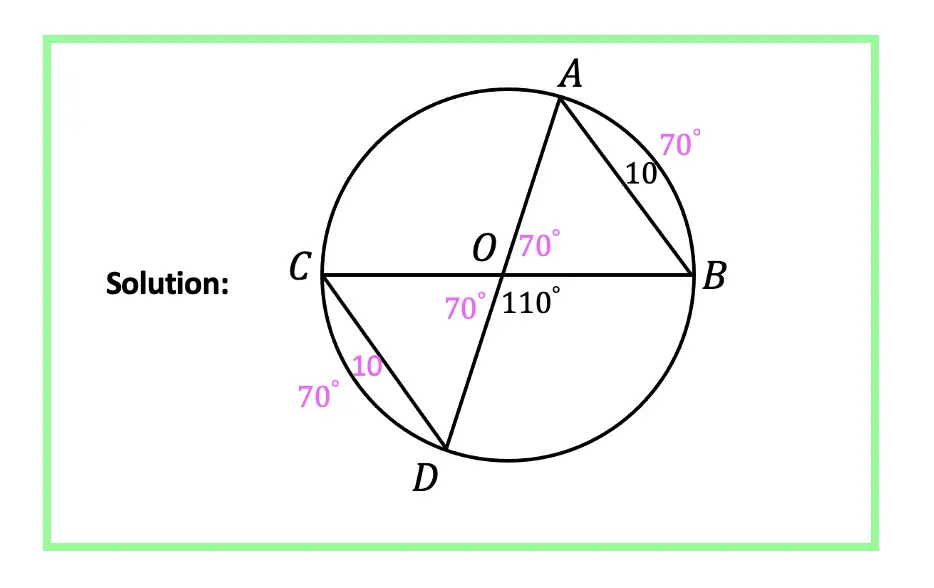
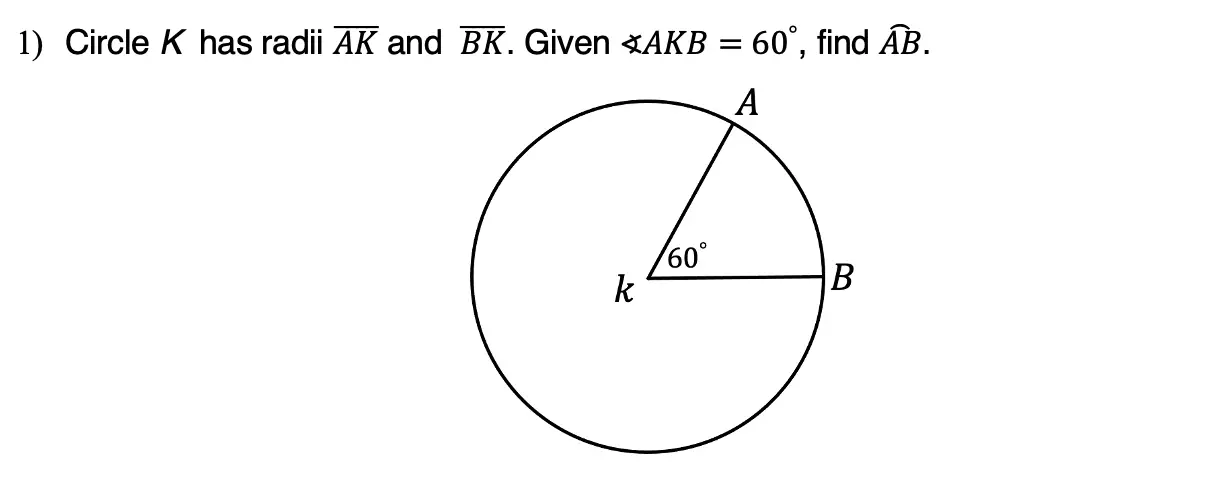
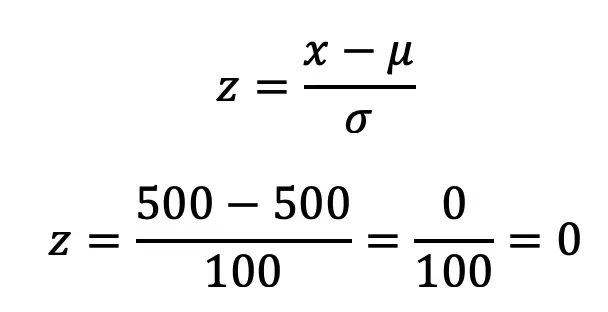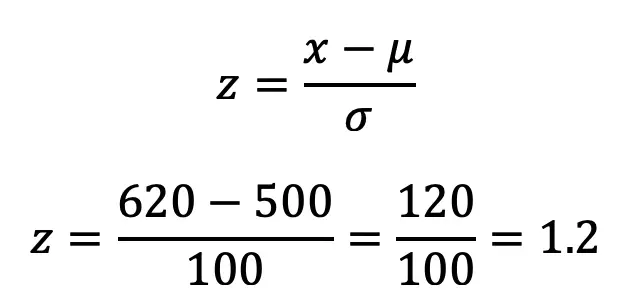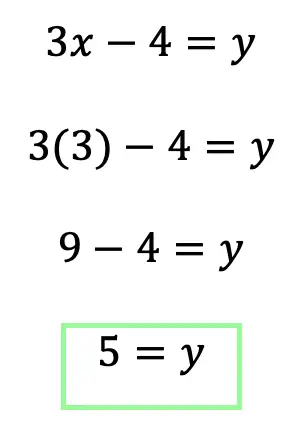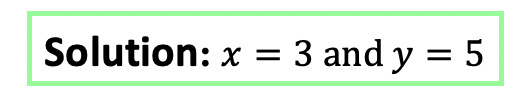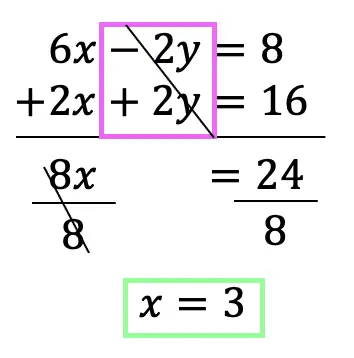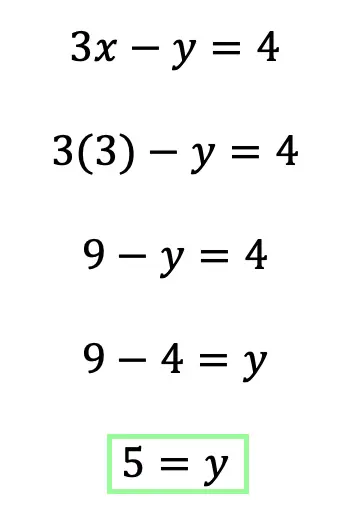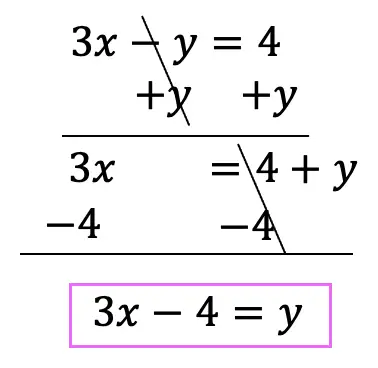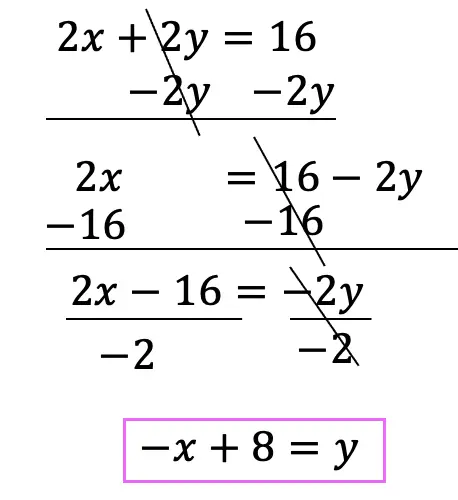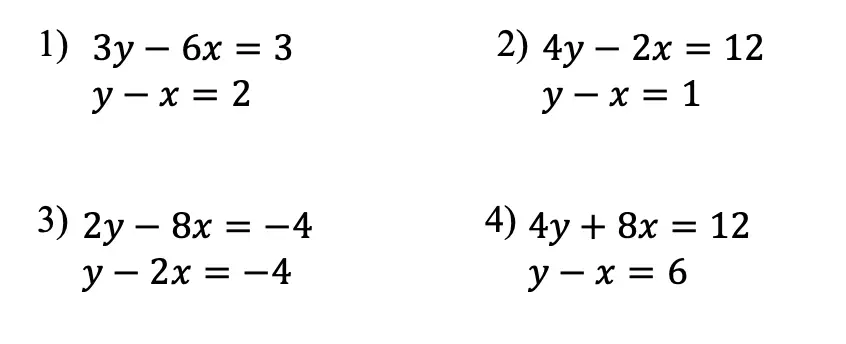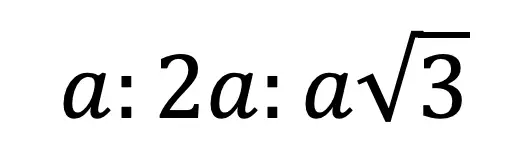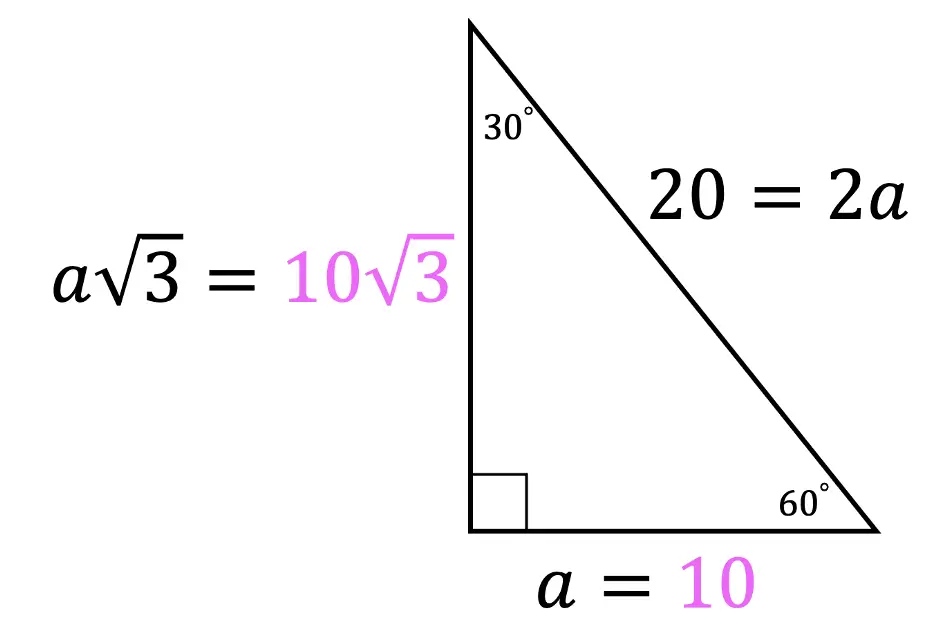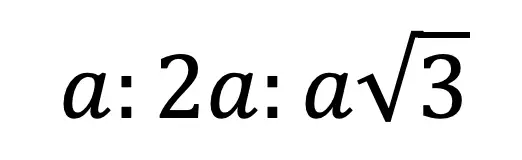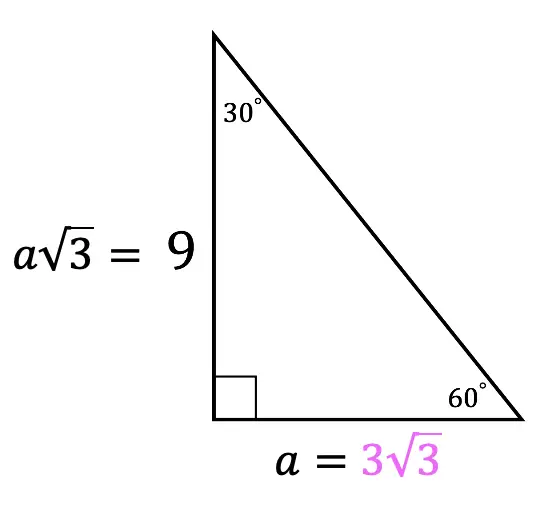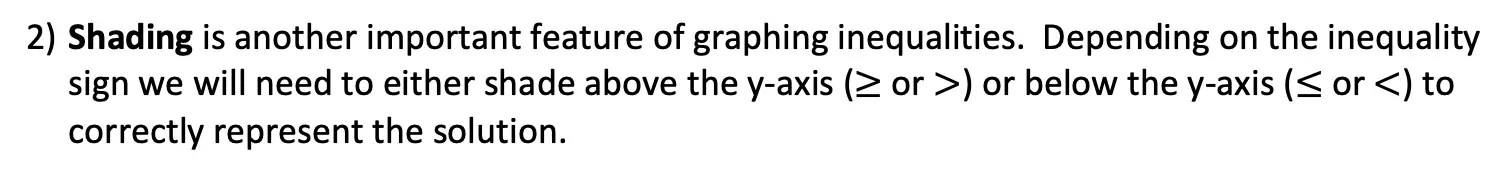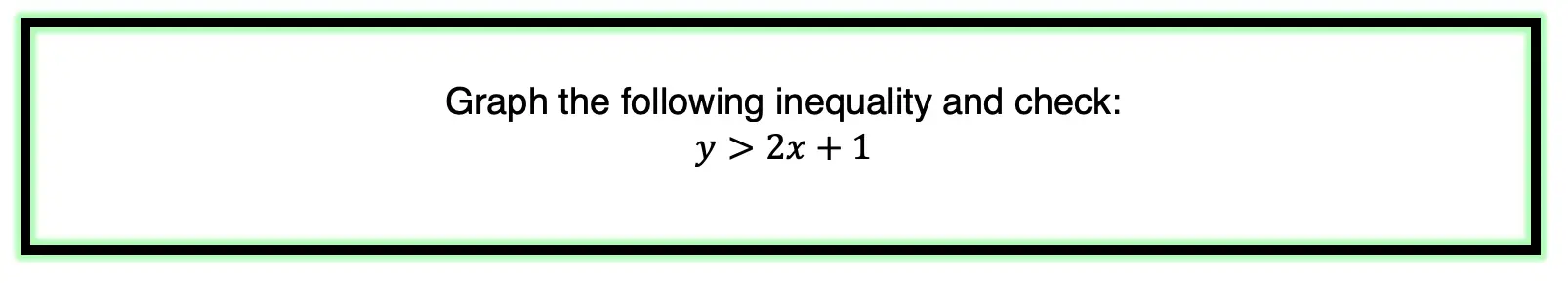Blog - Page 7 of 13 - Math Lessons

Square Inscribed in a Circle Construction

Greetings math friends and welcome to MathSux! In this week’s post, we are going to take a step-by-step look at how a square inscribed in a circle construction works! Within this post we have a video, a GIF, and a step-by-step written explanation below, the choice of learning how to do this construction is up to you! Happy Calculating! 🙂

How to Construct a Square Inscribed in Circle:

Step 1: First, we are going to draw a circle using a compass (any size).

Step 2: Using a ruler, draw a diameter or straight line across the length of the circle, going through its midpoint.

Step 3: Next, open up the compass across the circle. Then take the point of the compass to one end of the diameter and swing the compass above the circle, creating an arc.

Step 4: Keeping that same length of the compass, go to the other side of the diameter and swing above the circle again making another arc until the two arcs intersect.

Step 5: Now, we are going to repeat steps 3 and 4, this time creating arcs below the circle using the same compass size.

Step 6: Connect the point of intersection above and below the circle using a ruler or straight edge. This creates a perpendicular bisector, cutting the diameter in half and forming a 90º angle.

Step 7: Lastly, we are going to use a ruler to connect each corner point to one another creating a square!

Constructions and Related Posts:

Looking to construct more than just a square inside a circle? Check out these related posts and step-by-step tutorials on geometry constructions below!

Construct an Equilateral Triangle

Perpendicular Line Segment through a Point

Angle Bisector

Construct a 45º angle

Altitudes of a Triangle (Acute, Obtuse, Right)

How to Construct a Parallel Line

Bisect a Line Segment

Best Geometry Tools!

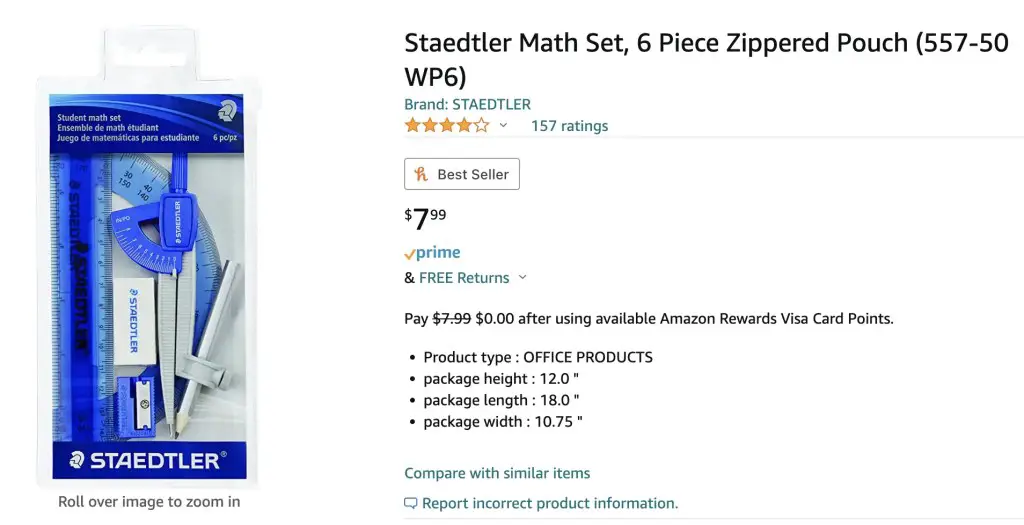
Looking to get the best construction tools? Any compass and straight-edge will do the trick, but personally, I prefer to use my favorite mini math toolbox from Staedler. Stadler has a geometry math set that comes with a mini ruler, compass, protractor, and eraser in a nice travel-sized pack that is perfect for students on the go and for keeping everything organized….did I mention it’s only $7.99 on Amazon?! This is the same set I use for every construction video in this post. Check out the link below and let me know what you think!

Still got questions? No problem! Don’t hesitate to comment with any questions or concerns below. Also if you’re looking for a different type of construction you don’t yet see here, please let me know! Happy calculating! 🙂

Let’s be friends! Check us out on the following social media platforms for even more free MathSux practice questions and videos:

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for something similar to square inscribed in a circle construction? Check out this post here on how to construct and equilateral triangle here! And if you’re looking for even more geometry constructions, check out the link here!

How to Calculate Z-Score?: Statistics

Hi there and welcome to MathSux! In this post, we are going to explore how to calculate z-score and the normal distribution. We’ll do this by examining the normal curve and learning how to find probability finding z-score and using the mean, standard deviation, and specific data points. Fore more info and more MathSix don’t forget to check out the video and practice questions below. Happy calculating!

What is a Normal Curve?

A normal curve is a bell shaped curve that shows the distribution of data evenly spread with respect to the mean. If you look at the normal curve below, the area under the curve shows all the possible probabilities of a certain data point occurring, notice the curve is higher towards the center mean, μ, and gets smaller as the distance from μ grows. The distance from μ is measured by the standard deviation, a unique unit of measurement that is specific to each group of data.

Mean: The mean always falls directly in the center of our normal curve. It is the average of our data, and always falls right in the middle.

Standard Deviation: This value is used as a standard unit of measurement for the data, measuring the distance between each data point in relation to the mean throughout the entire data set. For a review on what standard deviation is and how to calculate it, check out this post here.

Now for our normal curve:

Notice half of the data is below the mean, μ, while the other half is above? The normal curve is symmetrical about the mean, μ!

How to Calculate Z-Score?

Z Score can tell us at what percentile a certain point in the data set falls in relation to the rest of the mean by using the standard deviation as a unit of measurement. If this sounds confusing, it’s ok! Take a look at the following formula:

We use the above formula in conjunction with a z table which tells us the probability under the curve for a certain point.

Solution:

a) What percent of student scored below 500?

Step 1: First, let’s draw out our given information the mean=500, standard deviation=100, and the data point the question is asking for x=500 onto a normal curve. Notice that we want to find the value of the area under the curve shaded in pink. This will tell us the percent of students that scored below 500.

Step 2: We need to find the z-score by, using the data point given to us x=500, the mean=500, and the standard deviation, sigma=100.

Step 3: Yes, we have a zero! Now we need to take our z table and line up our chart. Notice that the chart finds the probability for everything at the beginning of the normal curve and on. This is perfect for answering our question!

Step 4: The table gives us our solution of .5000. If we multiply .5000 times 100 it gives us the percent of students who scored below 500 at 50%.

b) What percent of student scored above 620?

Step 1: First, let’s draw out our given information the mean=500, standard deviation=100, and the data point the question is asking for x=620 onto a normal curve. Notice that we want to find the value of the area under the curve shaded in pink. This will tell us the percent of students that scored above 620.

Step 2: We need to find the z-score by, using the data point given to us x=620, the mean=500, and the standard deviation, sigma=100.

Step 3: Yes, we got 1.2! Now we need to take our z table and line up our chart. Notice that the chart finds the probability for everything at the beginning of the normal curve and on. This is means to find the percent we are looking for, we need to subtract our answer from one since we want the value of probability on the right side of the curve (the z-table only provides the left side).

Step 4: The table gives us our solution of .8849. If we subtract this value from 1 then multiply that value times 100 it gives us the percent of students who scored above 620.

C) What is the highest score a student could receive if the students was in the 16.11^th percentile?

Step 1: In this question we have to work backwards by first identifying, where on the z-score table is the number .1611 and then filling in our z score formula to find x, the missing data point (in this case test score).

Search the table for .1611:

Notice that .1611 can be found on the z-table above with z-score -0.99. This is what we’ll use to find the unknown data point!

Step 2: We need to find the unknown test score by, using the z score we just found z=-0.99, the mean=500, and the standard deviation, sigma=100.

Step 3: Solve for x.

Practice Questions:

The grades on a final English exam are normally distributed with a mean of 75 and a standard deviation of 10.

a) What percent of students scored below a 60?

b) What percent of students scored above an 89?

c) What is the highest possible grade that included in the 4.46^th percentile?

d) What percent of students got at least a 77?

Solutions:

a) 6.68%

b) 8.08%

c) 58

d) 42.07%

Want to make math suck just a little bit less? Subscribe to my Youtube channel for free math videos every week! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Looking for more Statistics?

Difference between Bar Graphs and Histograms

Box and Whisker Plots

Variance and Standard Deviation

Expected Value

Simultaneous Equations: Algebra

Happy new year and welcome to Math Sux! In this post we are going to dive right into simultaneous equations and how to solve them three different ways! We will go over how to solve simultaneous equations using the (1) Substitution Method (2) Elimination Method and (3) Graphing Method. Each and every method leading us to the same exact answer! At the end of this post don’t forget to try the practice questions choosing the method that best works for you! Happy calculating! 🙂

What are Simultaneous Equations?

Simultaneous Equations are when two equations are graphed on a coordinate plane and they intersect at, at least one point. The coordinate point of intersection for both equation is the answer we are trying to find when solving for simultaneous equations. There are three different methods for finding this answer:

We’re going to go over each method for solving simultaneous equations step by step with the example below:

Method #1: Substitution

The idea behind Substitution, is to solve for 1 variable first algebraically, and the plug this value back into the other equation solving for one variable. Then solving for the remaining variable. If this sounds confusing, don’t worry! We’re going to do this step by step:

Step 1: Let’s choose the first equation and move our terms around to solve for y.

Step 3: The equation is set up and ready to solve for x!

Step 4: All we need to do now, is plug x=3 into one of our original equations to solve for y.

Step 5: Now that we have solved for both x and y, we have officially found where these two simultaneous equations meet!

Method #2: Elimination

The main idea of Elimination is to add our two equations together to cancel out one of the variables, allowing us to solve for the remaining variable. We do this by lining up both equations one on top of the other and adding them together. If variables at first do not easily cancel out, we then multiply one of the equations by a number so it can. Check out how it’s done step by step below!

Step 1: First, let’s stack both equations one on top of the other to see if we can cancel anything out:

Step 2: Our goal is to get a 2 in front of y in the first equation, so we are going to multiply the entire first equation by 2.

Step 3: Now that we multiplied the entire first equation by 2, we can line up our two equations again, adding them together, this time canceling out the variable y to solve for x.

Step 4: Now, that we’ve found the value of variable x=3, we can plug this into one of our equations and solve for missing unknown variable y.

Step 5: Now that we have solved for both x and y, we have officially found where these two simultaneous equations meet!

This image has an empty alt attribute; its file name is Screen-Shot-2020-12-30-at-10.21.46-AM.png

Method #3: Graphing

The main idea of Graphing is to graph each a equation on a coordinate plane and then see at what point they intersect. This is the best method to visualize and check our answer!

Step 1: Before we start graphing let’s convert each equation into y=mx+b (equation of a line) form.

Equation 1:

Equation 2:

Step 2: Now, let’s graph each line, y=3x-4 and y=-x+8, to see at what coordinate point they intersect.

Need to review how to draw an equation of a line? Check out this post here! Notice we got the same exact answer using all three methods (1) Substitution (2) Elimination and (3) Graphing.

Ready to try the practice problems on your own?! Check them out below!

Practice Questions:

Solve the following simultaneous equations for x and y.

Solutions:

(1, 3)
(4,5)
(-1, -6)
(3, -3)

Want more MathSux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating!

Facebook ~ Twitter ~ TikTok ~ Youtube

If you are looking for a challenge, try solving three equations with three unknown variables, in this post here!

30 60 90 Triangle

Hi everyone and welcome to MathSux! In this post, we are going to break down 30 60 90 degree special right triangles. What is it? Where did it come from? What are the ratios of its side lengths and how do we use them? You will find all of the answers to these questions about this right angled triangle in this post. Also, don’t forget to check out the video below and practice questions at the end of this post to truly become a 30 60 90 special right triangle master! Happy calculating! 🙂

If you want to learn about the other special triangle, 45 45 90 triangle, check out this post here. And if you’re looking to make math suck just a little bit less? Subscribe to our Youtube channel for free math videos every week! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

30 60 90 Triangle Ratio:

Notice that the 30 60 90 triangle is made up of one right angle across from the hypotenuse (which is always going to be the longest side), a 60 degree angle with a longer leg on the opposite side, and a 30 degree angle measure across from the shorter leg.

What is a 30 60 90 Triangle and why is it “Special”?

The 30 60 90 triangle is a special right triangle because it forms an equilateral triangle when a mirror image of itself is drawn. This means that all sides are equal when a mirror image of the triangle is drawn which allows us to find the ratio between each of the sides of the triangle by using the Pythagorean Theorem. Check it out below!

Now let’s draw a mirror image of our triangle to create an equilateral triangle. Next, we can label the length of the new side opposite 30 degrees (the shorter leg) “a,” and add this new mirror image length with the original we had to get, a total of a+a=2a.

If we look at our original 30 60 90 triangle, we now have the following values for each side based on our equilateral triangle. Notice we still need to find the length value of the longer leg, opposite angle 60 degrees.

Pythagorean Theorem Formula
Fill in values from our triangle longer leg
Distribute the exponent and start solving for our “?” by subtracting a^2 from both sides.
Now take the square root of both sides to solve for “?.” We have found a solution! Our missing side length is equal to a√3.

To sum up, we have applied the Pythagorean Theorem formula, filled in values found in our triangle for each length, distributed the exponent and subtracted a² from both sides, took the square root, and finally found our solution for our ratio for the longer leg opposite 60 degrees.

Now we can re-label our triangle, knowing the length of the hypotenuse in relation to the two legs. This creates a ratio that applies to all 30 60 90 triangles!

How do I use this ratio?

Knowing the above ratio, allows us to find any length of any and every 30 60 90 triangle, when given the value of one of its sides. Let’s tsee how this ratio works with some examples.

Example #1:

Step 1: First let’s look at our ratio and compare it to our given triangle.

Step 2: Notice we are given the value of a, which is equal to 4, knowing this we can now fill in each length of our triangle based on the ratio of a 30 60 90 triangle.

Now let’s look at another Example where we are given the length of the hypotenuse and need to find the values of the other two missing sides.

Example #2:

Step 1: First let’s look at our ratio and compare it to our given triangle.

Step 2: Notice we are given the value of the hypotenuse, 2a=20. Knowing this we can find the value of a by dividing 20 by 2 to get a=10. Once we have the value of a=10, we can easily find the length of the last, longer leg based on the 30 60 90 ratio:

Now for our last Example, we will see how to find the value of the shorter leg and hypotenuse, when we are given the side length of the longer leg across from 60º and need to find the other two missing sides.

Example #3:

Step 1: First let’s look at our ratio and compare it to our given triangle.

Step 2: In this case, we need to use little algebra to find the value of a, using the ratio for 30 60 90 triangles.

We set up this equation, knowing that 9 is across from 60 degrees, and that a√3=9. To solve for a, we divide square root both sides by √3. We get a solution a=9/√3! Yay! We cannot have a radical in the denominator, so we rationalize the denominator by multiplying the numerator and denominator by √3.

Now that we have one piece of the puzzle, the value of a, let’s fill in the value of the shorter leg of our triangle below:

Finally, let’s find the value of the length of the hypotenuse, which is equal to 2a in our ratio. Knowing the length of all sides, we can fill in the lengths of each side of our triangle for our solution.

Think you are ready to master these types of questions on your own? Try the practice problems below!

Practice Questions:

Find the value of the missing sides of each 30 60 90 degree triangle.

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

NYE Ball Fun Facts: Volume & Combinations

Greetings math friends, and Happy New Year! In today’s post we’re going do something a little different and take a look at the math behind the very famous and very shiny New Year’s Eve Ball that drops down every year at midnight. We’ll break down the shape, the volume, and the number of those dazzling Waterford crystals (and no this post isn’t sponsored) and look at some NYE Ball Fun Facts.

NYE Ball Fun Facts

Shape: Geodesic Sphere

Yes, apparently the shape of the New Year’s ball is officially called a “Geodesic Sphere.” It is 12 feet in diameter and weighs 11,875 pounds.

Volume (Estimate): 288π ft³

If we wanted to estimate the volume of the New Year’s Ball we would could use the formula for volume of a sphere:

Number of Waterford Crystals: 2,688

Talk about the ultimate shiny bauble! The NYE ball lights up the night with all 2,688 crystals in the shape of different sized triangles, each with heights of 5.75 inches or 4.75 inches.

Number of Lights: 48 light emitting diodes (LED’s)

On each triangle, there are 48 LEDs: 12 red, 12 blue, 12 green, and 12 white, for a total of 32,256 LEDs on the entire NYE ball itself.

Permutations and Combinations:

Permutations: With this many lights and colors, there are over a billion potential permutations of colors on the entire NYE ball.

Combinations: Let’s break down one triangle with 48 LED lights each with 12 red, 12 blue, 12 green, and 12 white LEDs. How many possible combinations of lights are possible if we were to choose 7 blue, 5 red, 10 green, and 1 white turned on all at the exact same time?

We end up with the combination formula below:

That means that there are 496,793,088 possible ways that 7 blue lights, 5 red lights, 10 green lights, and 1 white light can be lit up on a triangle that is part of the entire NYE ball!

Interested in more NYE fun facts? Check out the sources of this article here.

NYE Fact Sheet from: timessquarenyc.org

NYE Ball picture: Timesquareball.net

If you like finding the volume of the NYE ball maybe, you’ll want to find the volume of the Hudson Yards Vessal in NYC here. Happy calculating and Happy New Year from MathSux!

Facebook ~ Twitter ~ TikTok ~ Youtube

Transforming Trig Functions: Amplitude, Frequency, Period, Phase Shifts

Hi everyone, and welcome to MathSux! In this post, we are going to break down transforming trig functions by identifying their amplitude, frequency, period, horizontal phase shift, and vertical phase shifts. Fear not! Because we will break down what each of these terms (amplitude, frequency, period, horizontal phase shift and vertical phase shifts) mean and how to find them when looking at a trigonometric function and then apply each of these changes step by step to our graph. In this particular post, we will be transforming and focusing on a cosine function, but keep in mind that the same rules apply for transforming sine functions as well (example shown below in practice).

And if you’re ready for more, check out the video and the practice problems below, happy calculating! 🙂

*For a review on how to derive the basic Trig functions (y=sinx, y=cosx, and y=tanx), click here.

What are the Different Parts of a Trig Function?

When transforming trig functions, there are several things to look out for, let’s take a look at what each part of a trig function represents below:

Amplitude: The distance (or absolute value) between the x axis and the highest point on the graph.

Frequency: This is the number of cycles that happen between 0 and 2π. (Α “cycle” in this case is the number of “s” cycles for the sine function).

Period: The x-value/length of one cycle. (Α “cycle” in this case is the number of “s” cycles for the sine function). This is found by looking at the graph and seeing where the first cycle ends, or, by using the formula:

Horizontal Shift: When a trigonometric function is moved either left or right along the x axis.

Vertical Shift: When a trigonometric function is moved either up or down along the y axis.

Let’s try an Example, by graphing the following trig function step by step by identifying the amplitude, frequency, period, vertical shift, and horizontal phase shift.

Step 1: First let’s label and identify all the different parts of our trig function and what each part represents.

Step 2: Now let’s transform our trig graph one step at a time. First, let’s start graphing y=cos(x) without any transformations, the basic graph.

Step 3: Next, let’s add our amplitude of 2, otherwise known as the height, or distance to the x-axis. To do this our highest and lowest points on the y-axis will now be moved to 2 and -2 respectively.

Step 4: Next, we can apply our horizontal shift to the left by (π/2) or 90º. To do this, we need to look at where negative (π/2) is on our graph at (-π/2) and move our entire graph over to start at this new point, “shifting” over each coordinate point by (π/2) along the x axis.

Step 5: For our last transformation, we have a vertical phase shift up 1 unit. All this means is that we are going to shift our entire graph up by 1 unit along the y axis.

Trig function graph
phase shift
vertical shift — Shift our entire graph y=2cos(x+(π/2)) up one unit along the y-axis to get y=2cos(x+(π/2))+1

Think you are ready to try graphing trig functions and identifying the amplitude, frequency, period, vertical phase shift, and horizontal phase shift? Check out the practice questions and answers below!

Practice Questions:

When you’re ready check out the function transformations solutions below:

Solutions:

Still, got questions? No problem! Don’t hesitate to comment with any questions or check out the video above for an in-depth explanation. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Graphing Linear Inequalities: Algebra

graphing linear inequalities

Hi and welcome to MathSux! In this post, we are going to go over the rules for graphing linear inequalities on a coordinate plane when it comes to drawing lines, circles , and shading, then we are going to solve an example step by step. If you have any questions, check out the video below and try the practice questions at the end of this post! If you still have questions, don’t hesitate to comment below and happy calculating! 🙂

Graphing Linear Inequalities:

When graphing linear inequalities, we always want to treat the inequality as an equation of a line in form y=mx+b….with a few exceptions:

inequality shading above or below y-axis

Now that we know the rules, of graphing inequalities, let’s take a look at an Example!

Graphing Linear Inequalities Example:

Step 1: First, let’s identify what type of inequality we have here. Since we are working with a > sign, we will need to use a dotted line and open circles when creating our graph.

Step 2: Now we are going to start graphing our linear inequality as a normal equation of a line, by identifying the slope and the y-intercept only this time keeping open circles in mind. (For a review on how to graph regular equation of a line in y=mx+b form, click here)

Step 3: Now let’s connect our dots, by using a dotted line to represent our greater than sign.

Step 4: Now it is time for us to shade our graph, since this is an inequality, we need to show all of our potential solutions with shading. Since we have a greater than sign, , we will be shading above the y-axis. Notice all the positive y-values above are included to the left of our line. This is where we will shade.

Step 5: Check! Now we need to check our work. To do that, we can choose any point within our shaded region, if the coordinate point we chose hold true when plugged into our inequality then we are correct!

Let’s take the point (-3,2) plugging it into our inequality where x=-3 and y=2.

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above for an in depth explanation. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Central Angles Theorems: Geometry

Hi everyone, and welcome to MathSux! In this post, we are going to go over the Central Angles Theorems of circles. We’ll go over the theorems associated with central angles and then solve a quick example. Make sure to test your understanding of central angles and arcs with the practice questions at the end of this post. And, if you want more, don’t forget to check out the video below, happy calculating!

Central Angles and Arcs:

Central angles and arcs form when two radii are drawn from the center point of a circle. When these two radii come together they form a central angle. A central angle is equal to the length of the arc. When it comes to measuring the central angle, the central angle is always equal to arc length and vice versa:

Central Angles = Arc Length

Central Angle Theorems:

There are a two central angle theorems to know, check them out below!

Central Angle Theorem #1:

Central Angle Theorem #2:

Let’s look at how to apply these rules with an Example:

Let’s do this one step at a time.

Practice Questions:

Solutions:

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Circle Theorems & Formulas

Intersecting Secants Theorem

Inscribed Angles & Intercepted Arcs

Area of a Sector

Circle Theorems

TikTok Math Video Compilations

Happy December everyone! With ~~crazy~~ 2020 coming to an end, I thought I would share some TikTok math video compilations of Algebra, Geometry, Algebra 2/Trig, and Statistics for a quick review of all our videos posted throughout the year. Enjoy these TikTok math video compilations and happy calculating! 🙂

Want to make math suck just a little bit less? Subscribe and follow us for FREE fun colorful math videos and lessons every week! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Algebra:

Within algebra, you will find arithmetic sequences, combining like terms, box and whisker plots, geometric sequences, solving radical equations, completing the square, 4 ways to factor quadratic equations, piecewise functions and more!

Geometry:

Within Geometry, you will find, how to construct an equilateral triangle, a median of a trapezoid, area of a sector, how to find perpendicular and parallel lines through a given point, SOH CAH TOA right triangle trigonometry, reflections, and more!

Algebra 2/Trig.

Within Algebra 2/Trig., you will find, how to expand a cubed binomial, how to divide polynomials, how to solve log equations, imaginary numbers, synthetic division, unit circle basics, how to graph y=sin(x), and more!

Statistics:

Within statistics, you will find, box and whisker plots, how to find the variance, and, the probability of flipping a coin 2 times!

For full length video, don’t forget to check out our free math video index page! Thanks for stopping by! 🙂

Graphing Trig Functions: Algebra 2/Trig.

Hi everyone and welcome to MathSux! This post is going to help you pass Algebra 2/Trig. In this post, we are going to apply our knowledge of the unit circle and trigonometry and apply it to graphing trig functions y=sin(x), y=cos(x), and y=tan(x). We have been using trig functions in basic trigonometry, but today, we will see what each function (sin, cos, and tan) look like graphed on a coordinate plane.

If you are already familiar with the basics of graphing trig functions and want to learn how to transform them, including knowing how to identify the amplitude, period frequency, vertical shift, and horizontal phase shift, then please check out this post here on transforming trigonometric functions.

If you have any questions, don’t hesitate to comment or check out the video below. Thanks for stopping by and happy calculating! 🙂

How do we get coordinate points for graphing Trigonometric Functions?

For deriving our trigonometric function graphs [y=sin(x), y=cos(x), and y=tan(x)] we are going to write out our handy dandy Unit Circle. By looking at our unit circle and remembering that coordinate points are in (cos(x), sin(x)) form and that tanx=(sin(x))/(cos(x)) we will be able to derive each and every trig graph!

*Note below is the unit circle we are going to reference to find each value, for an in-depth explanation of the unit circle, check out this link here.

How to Graph y=sin(x)?

While Graphing Sine, you may notice that the sine function curves creates what looks like an “S” shape. As they say, “S” is for Sine, this is the easiest way to remember what the sine function looks like! Check it out below.

Now that we know what the sine function looks like once it’s graphed, let’s see why it looks that way in the first place by deriving each coordinate point with the help of the unit circle.

Step 1: We are going to derive each degree value for sin by looking at the unit circle. These will be our coordinates for graphing y=sin(x). *For a review on how to get these values, check out the link here explaining the unit circle.

Step 2: Now we need to convert all the x-values from degrees to radians. Fear not because this can be done easily with a simple formula!

To convert degrees à radians, just use the formula below:

Step 3: Now that we have our coordinate points and converted degrees to radians, we can draw out our function y=sin(x) on the coordinate plane!

Now we will follow the same process for graphing y=cos(x) and y=tan(x).

How to Graph y=cos(x)?

While Graphing Cosine, you may notice that the cosine function creates what looks like a “V” shape. I always like to think “V” is for victory, but of course, in this case, it is for cosine, that is the easiest way to remember what this function looks like! Check it out below.

Now that we know what the cosine function looks like once graphed, let’s see why it looks this way in the first place by deriving each coordinate point with the help of the unit circle.

Step 1: We are going to derive each degree value for cos by looking at the unit circle. These will be our coordinates for graphing y=cos(x). *For a review on how to get these values, check out the link here explaining the unit circle.

Step 2: Now we need to convert all the x-values from degrees to radians.

Step 3: Now that we have our coordinate points and converted degrees to radians, we can draw out our function y=cos(x) on the coordinate plane!

What do you think would happen if we were to vertical shift our entire function up by one unit? Or move our entire function to the left by 90 degrees with a horizontal phase shift? Check out what happens here!

How to Graph y=tan(x)?

While Graphing Tangent, you may notice that the tangent function looks totally different than sine or cosine. Check it out below.

Step 1: We are going to derive each degree value for the tangent function by looking at the unit circle. In order to derive values for tan(x), we need to remember that tan(x)=sin(x)/cos(x). Once found, these will be our coordinates for graphing y=tan(x). *For a review on how to get these values, check out the link here explaining the unit circle.

Step 2: Now we need to convert all the x-values from degrees to radians.

Step 3: Now that we have our coordinate points and converted degrees to radians, we can draw out our function y=tan(x) on the coordinate plane!

Still got questions? No problem! Don’t hesitate to comment with any questions or check out the video above for an in-depth explanation. Happy calculating! 🙂

Facebook ~ Twitter ~ TikTok ~ Youtube

Ready for the next lesson? Now that you know the basics of graphing the sine, cosine, and tangent functions, learn how to transform each trig function on a coordinate plane by identifying the amplitude, period frequency, vertical shift, and horizontal phase shift of each function, by checking out this post here on transforming trigonometric functions. When you’re ready for more, check out the related trig posts below!

How to Construct a Square Inscribed in Circle:

Constructions and Related Posts:

Best Geometry Tools!

What is a Normal Curve?

How to Calculate Z-Score?

Solution:

a) What percent of student scored below 500?

b) What percent of student scored above 620?

C) What is the highest score a student could receive if the students was in the 16.11th percentile?

Practice Questions:

Solutions:

Looking for more Statistics?

What are Simultaneous Equations?

Method #1: Substitution

Method #2: Elimination

Method #3: Graphing

Practice Questions:

Solutions:

30 60 90 Triangle Ratio:

What is a 30 60 90 Triangle and why is it “Special”?

How do I use this ratio?

Example #1:

Example #2:

Example #3:

Practice Questions:

Solutions:

Related Trigonometry Posts:

NYE Ball Fun Facts

Shape: Geodesic Sphere

Volume (Estimate): 288π ft3

Number of Waterford Crystals: 2,688

Number of Lights: 48 light emitting diodes (LED’s)

Permutations and Combinations:

What are the Different Parts of a Trig Function?

Practice Questions:

Solutions:

Related Trigonometry Posts:

Graphing Linear Inequalities:

Graphing Linear Inequalities Example:

Practice Questions:

Solutions:

Central Angles and Arcs:

Central Angle Theorems:

Practice Questions:

Solutions:

Circle Theorems & Formulas

Algebra:

Geometry:

Algebra 2/Trig.

Statistics:

How do we get coordinate points for graphing Trigonometric Functions?

How to Graph y=sin(x)?

How to Graph y=cos(x)?

How to Graph y=tan(x)?

Related Trigonometry Posts:

C) What is the highest score a student could receive if the students was in the 16.11^th percentile?

Volume (Estimate): 288π ft³