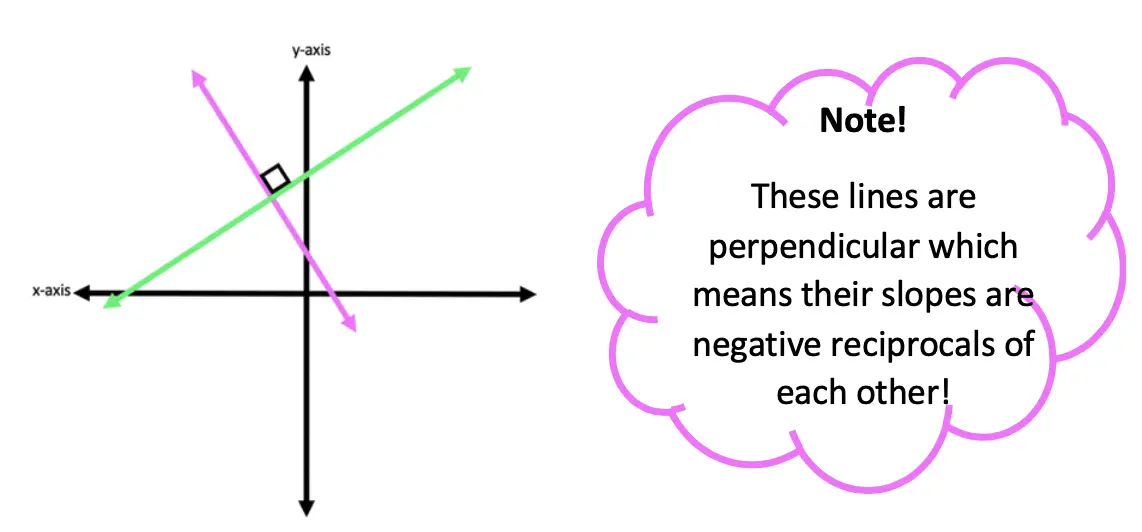
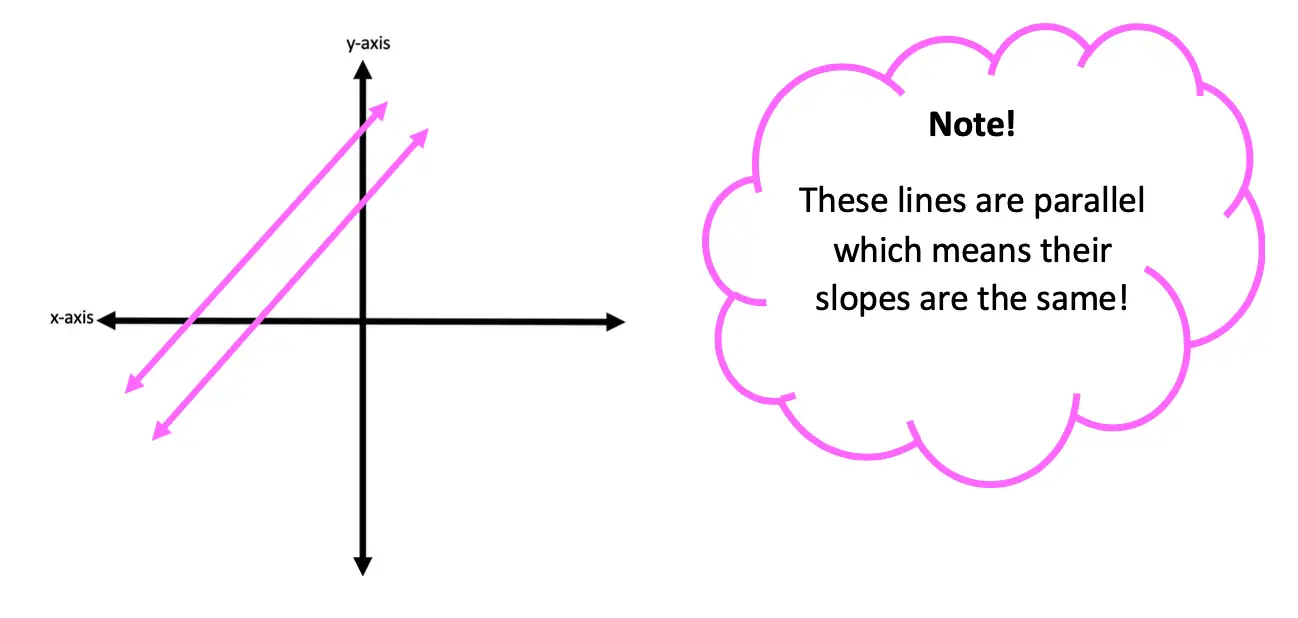
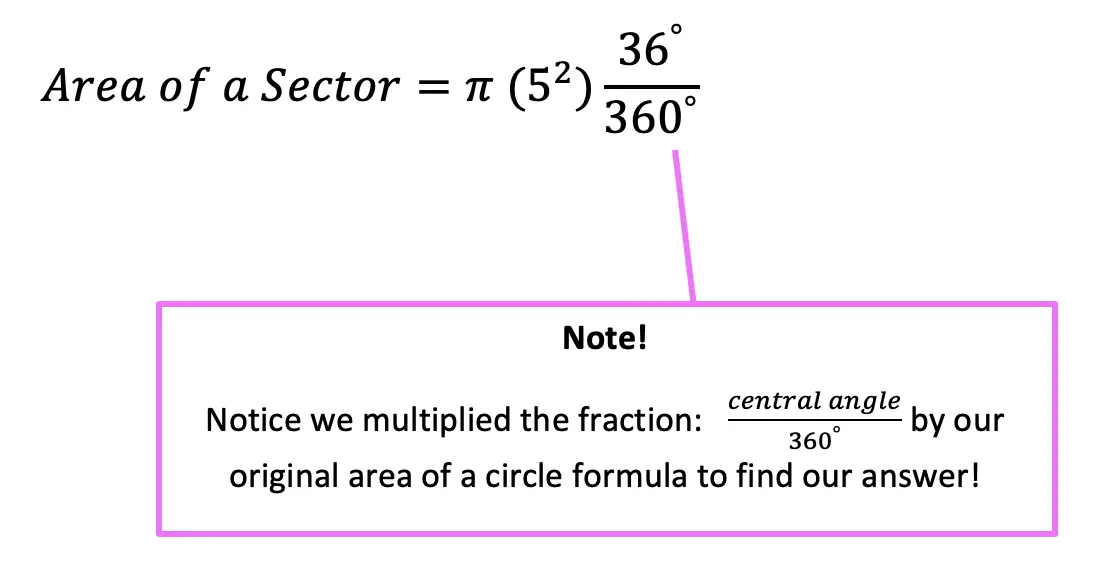
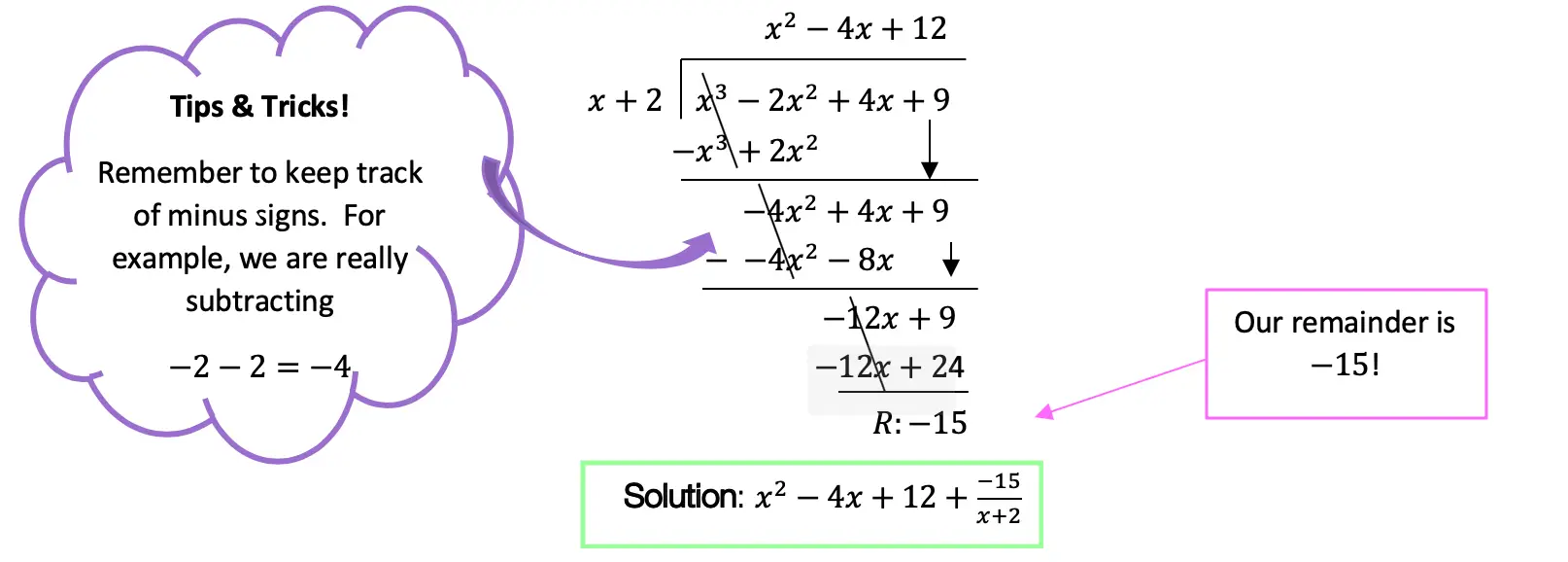
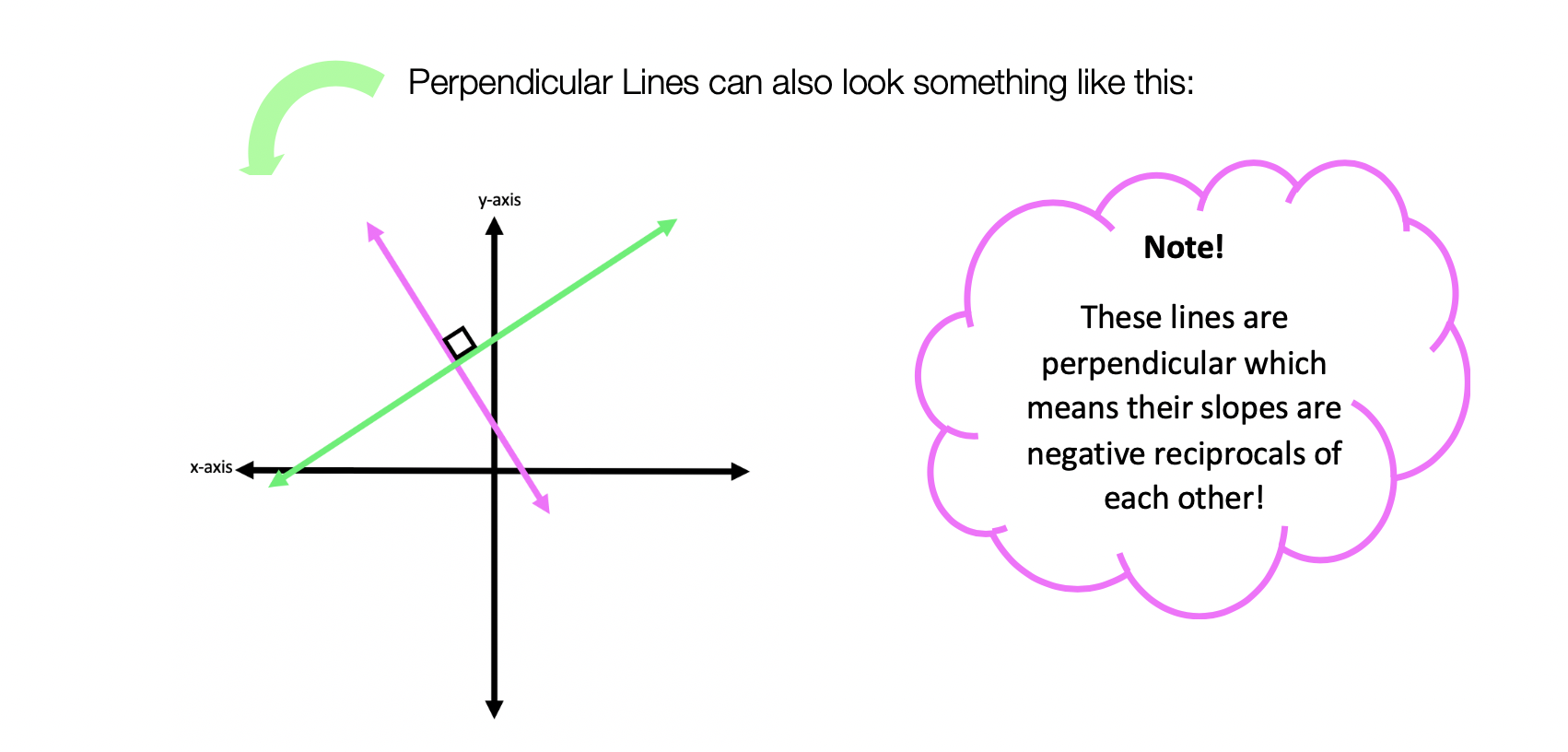
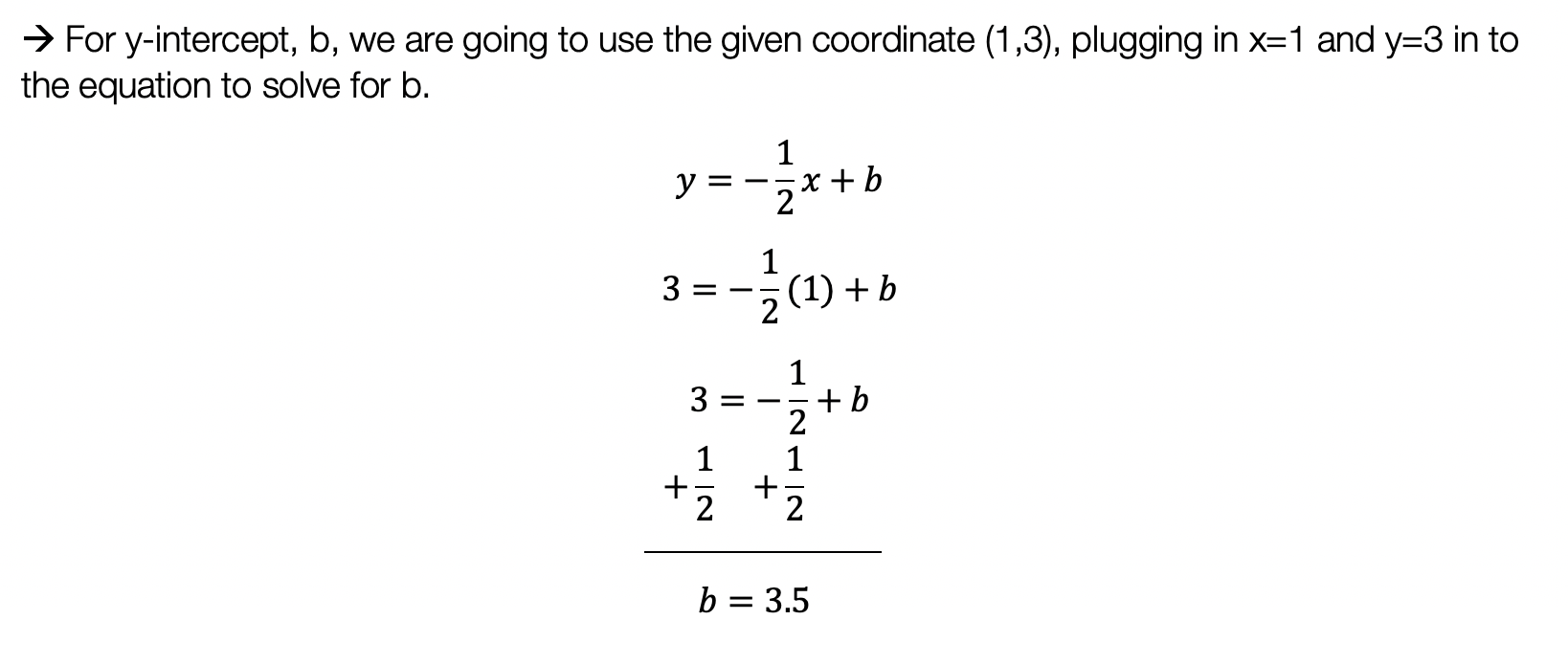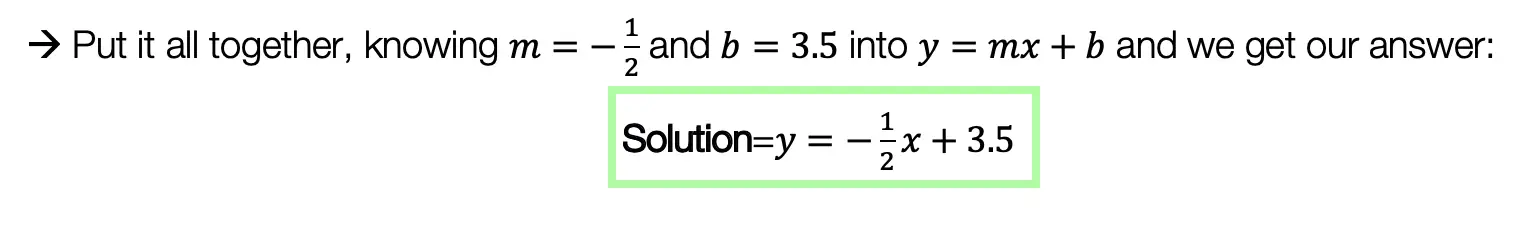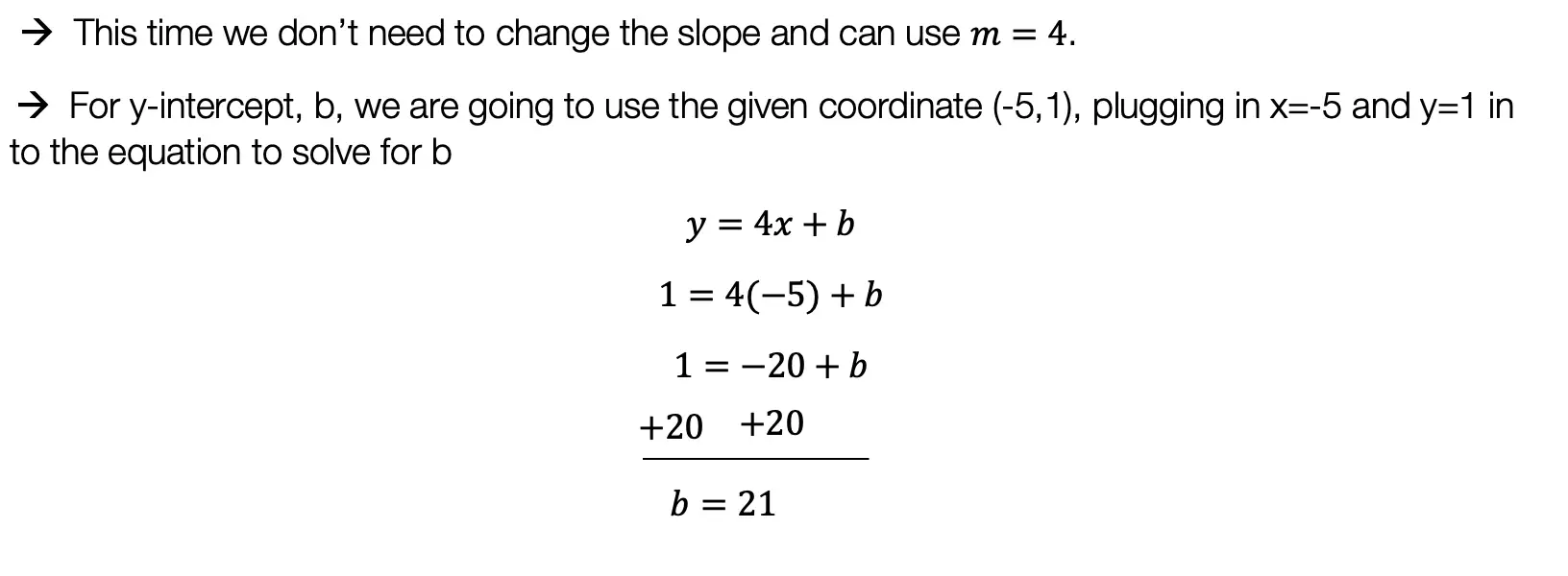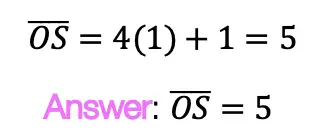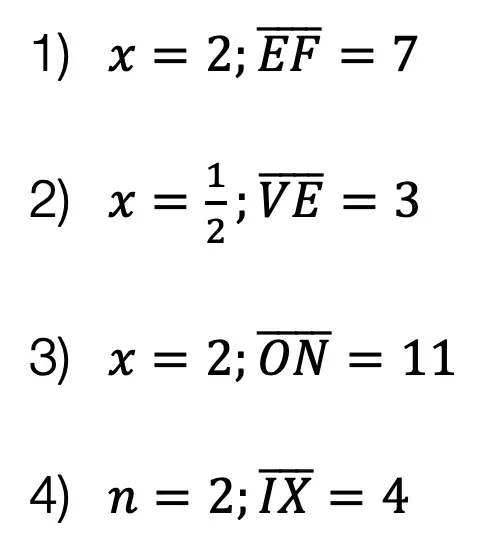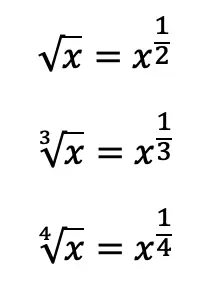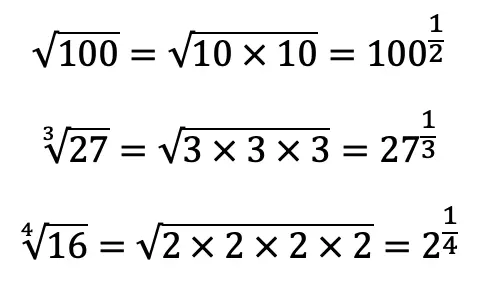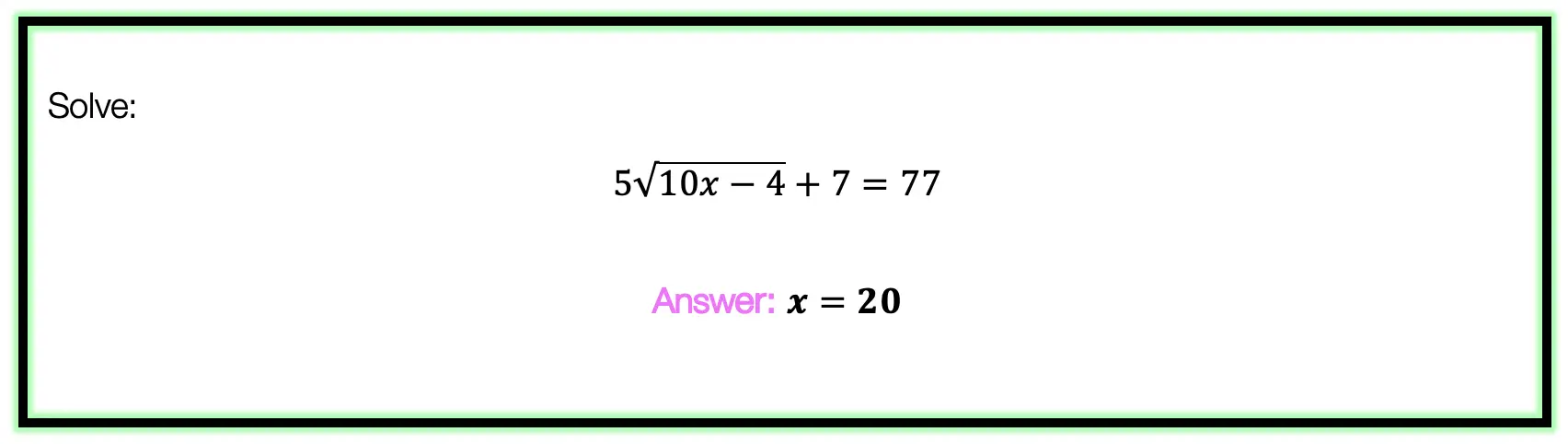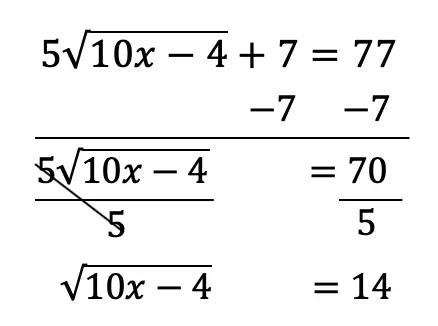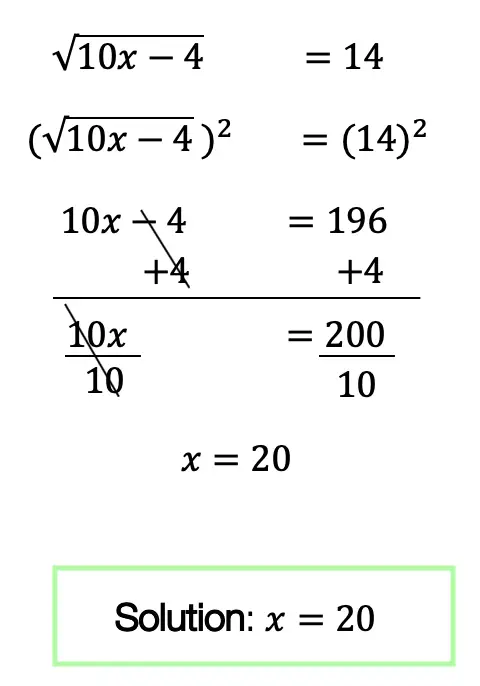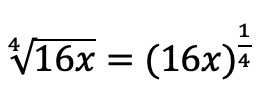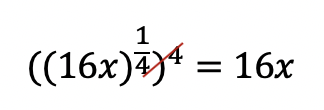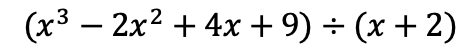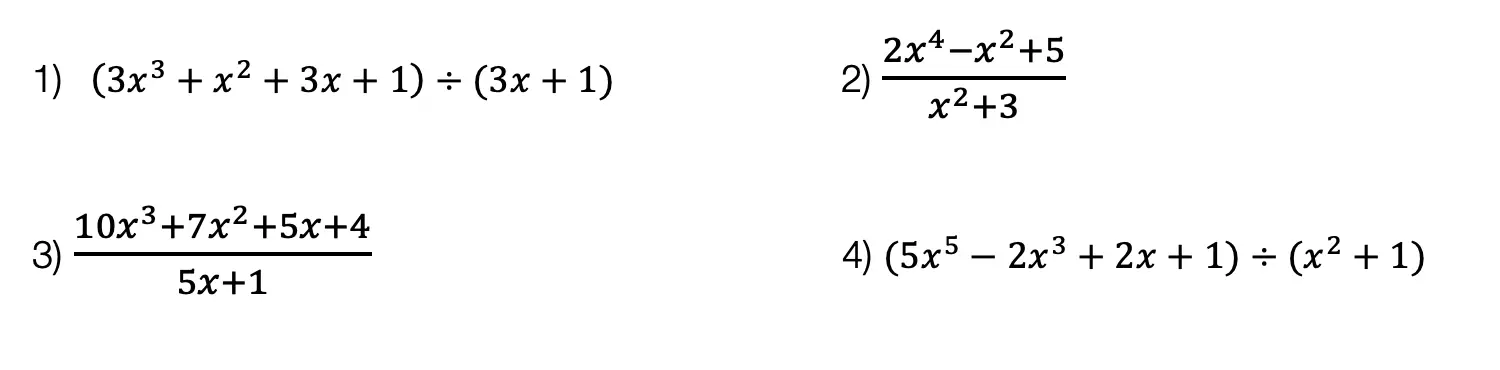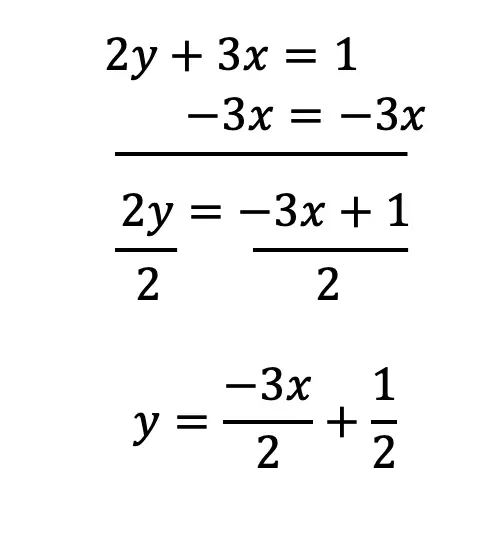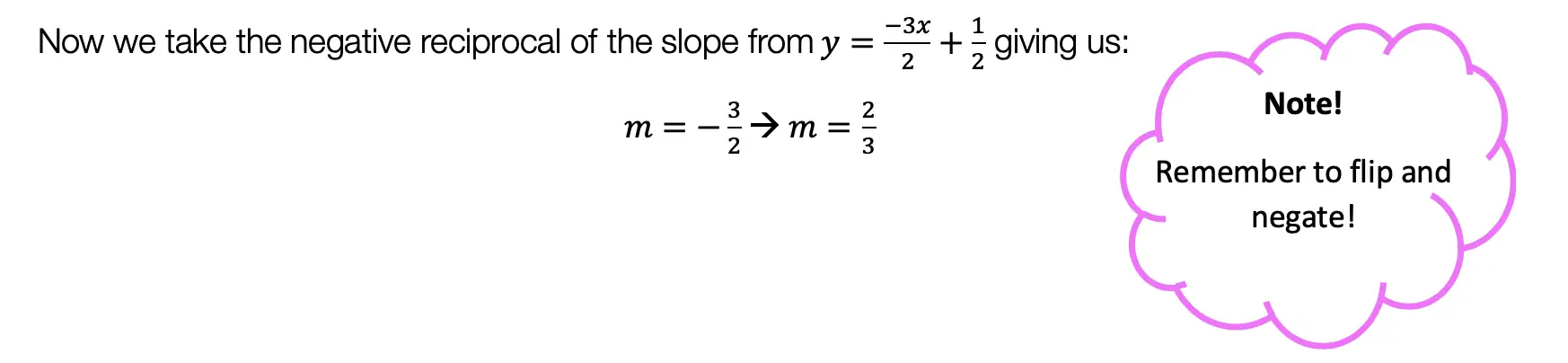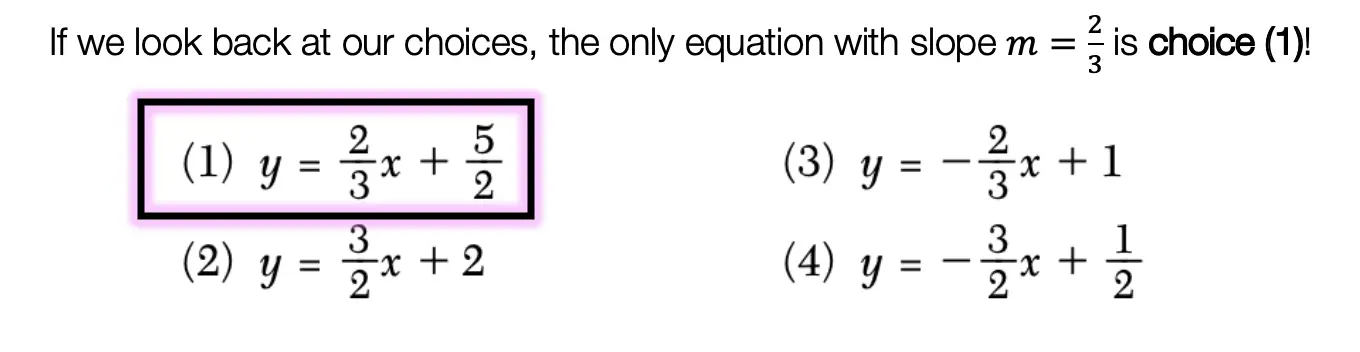Hi everyone, welcome back to Mathsux! This week we’ll be reviewing how to graph an equation of a line in y=mx+b form. And if you have not checked out the video below, please do! Happy calculating! 🙂
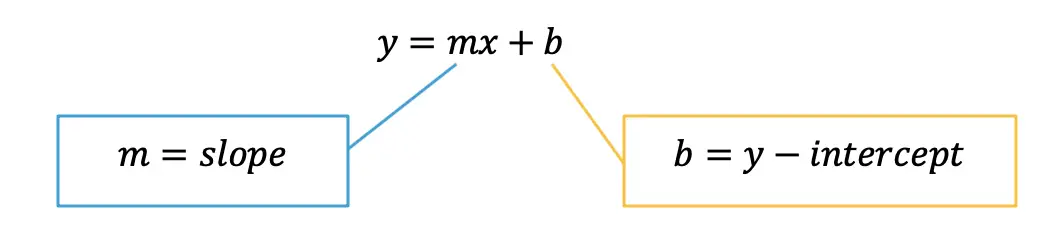
An equation of a line can be represented by the following formula:
y=mx+b
Y-Intercept: This is represented by b, the stand-alone number in y=mx+b. This represents where the line hits the y-axis. This is always the first point you want to start with when graphing at coordinate point (0,b).
Slope: This is represented by m, the number next to x in y=mx+b. Slope tells us how much we go up or down the y-axis and left or right on the x- axis in fraction form:
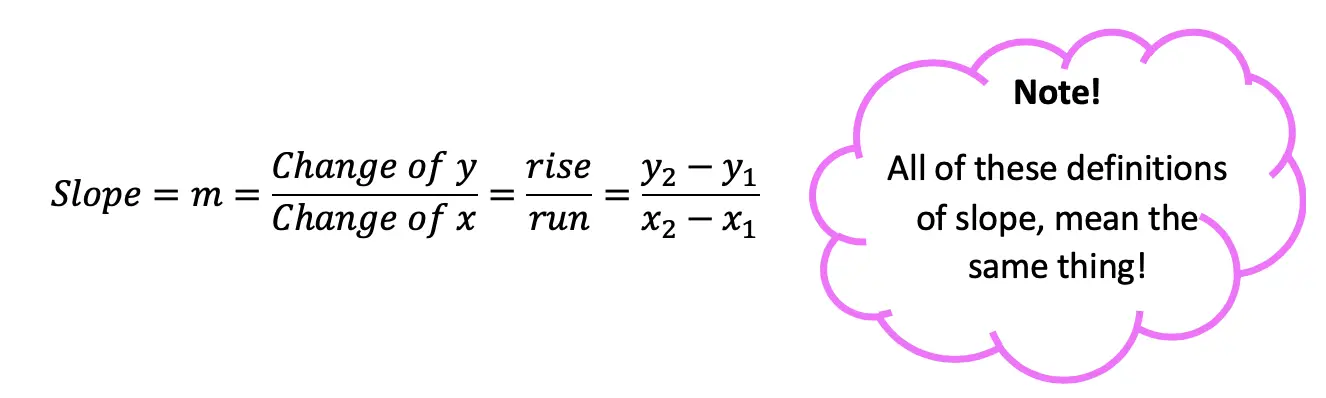
Now let’s check out an Example!
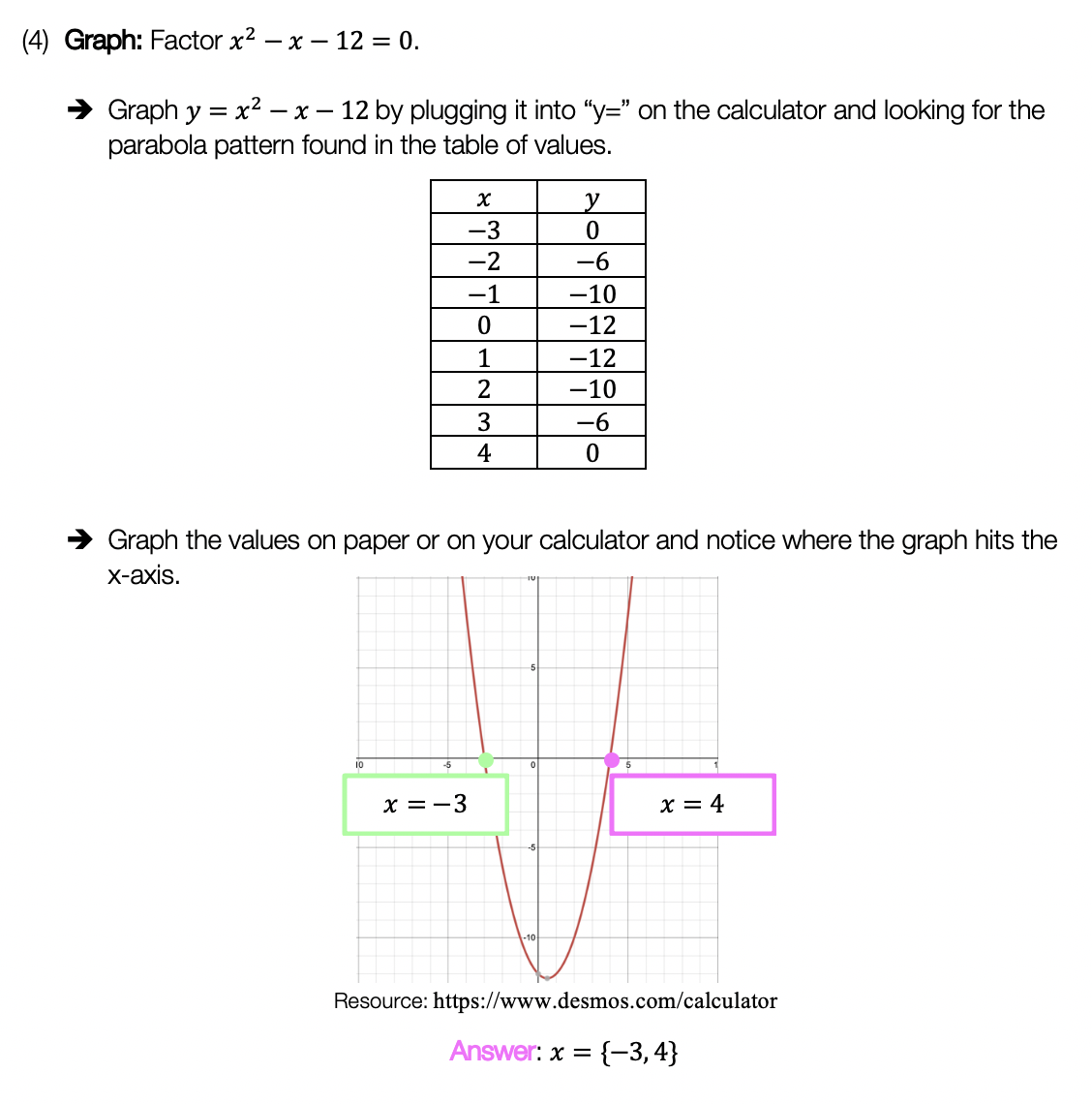
Graph the following:
![]()
-> First, let’s identify the slope and y-intercept of our line.
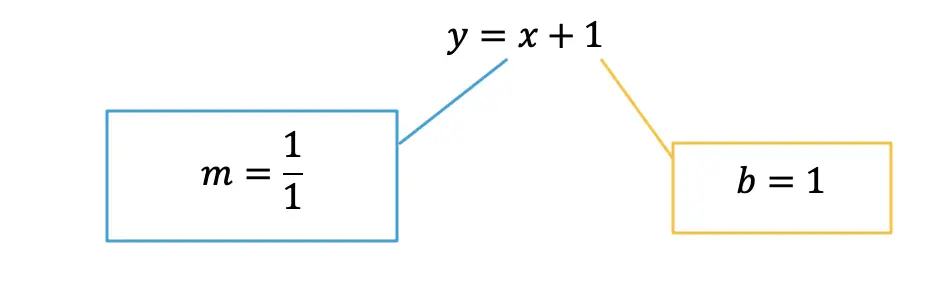
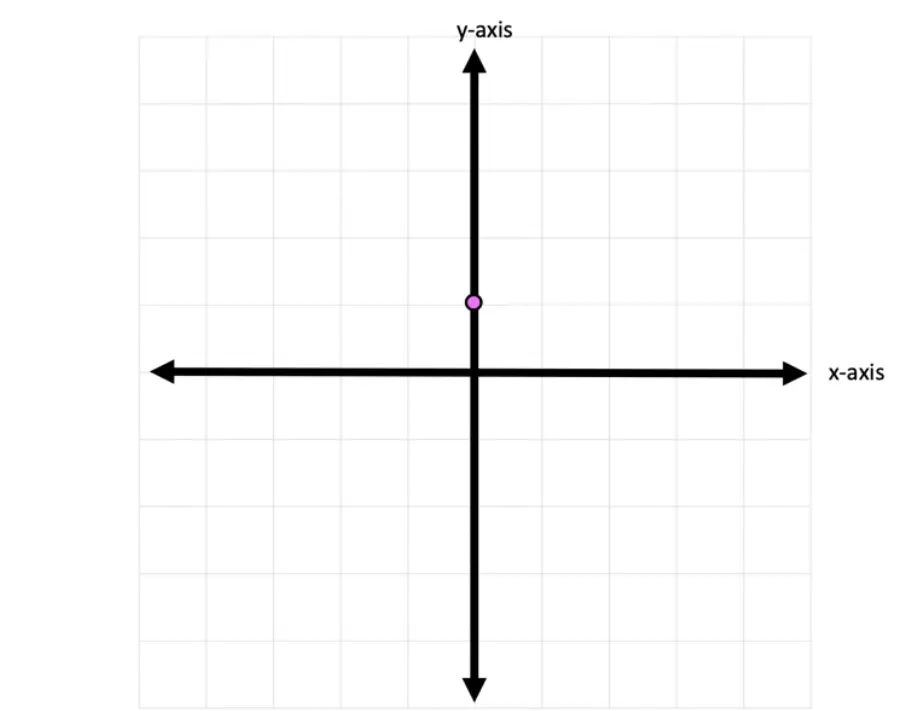
-> To start, let’s graph the first point on our graph, the y-intercept at point (0,1):
-> Now for the slope. We are going to go up one and over to the right one for each point, since our slope is 1/1.
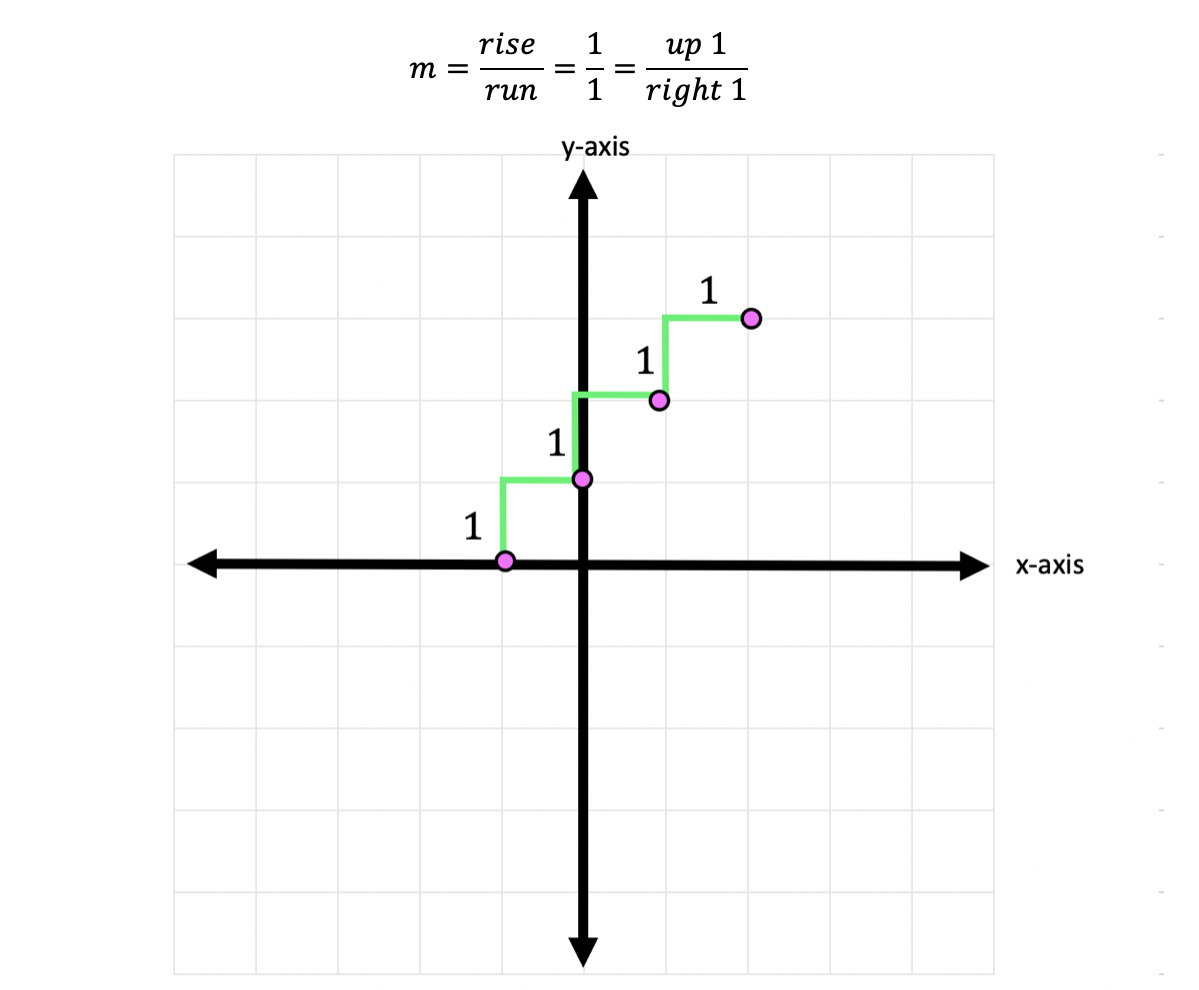
-> Connect all of our coordinate points and label our graph.
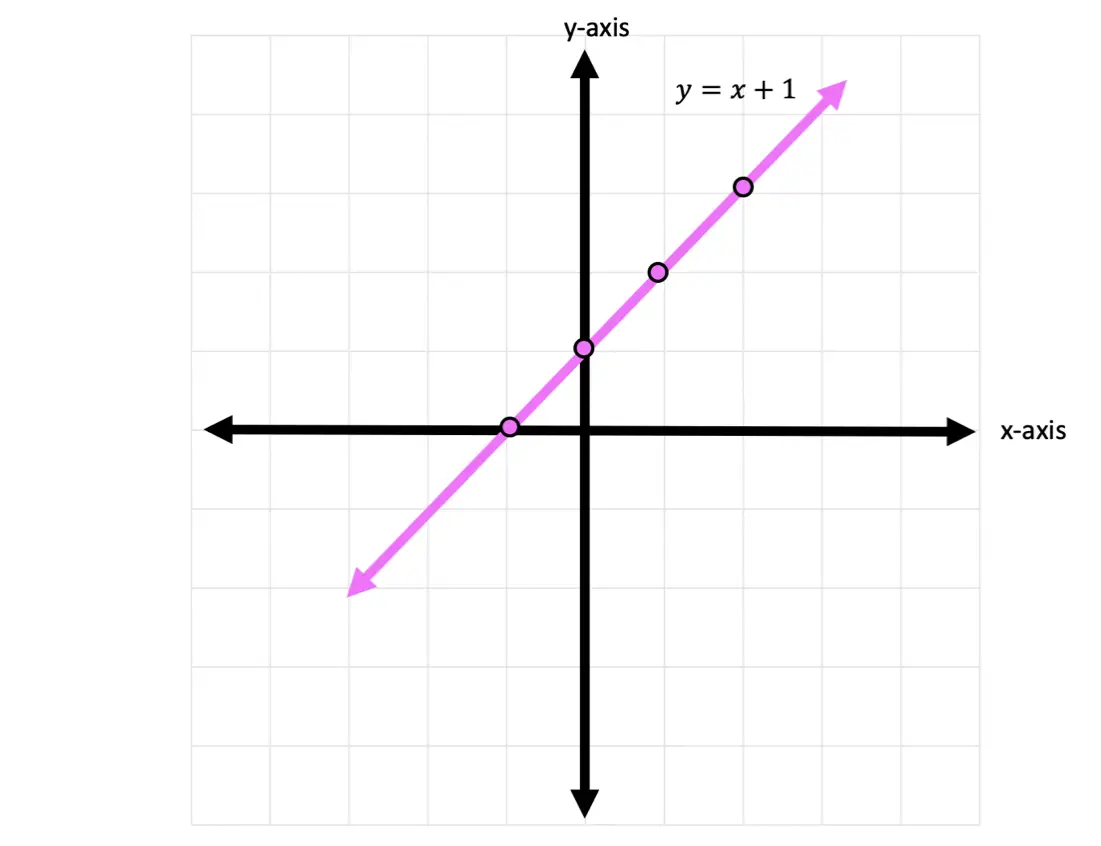
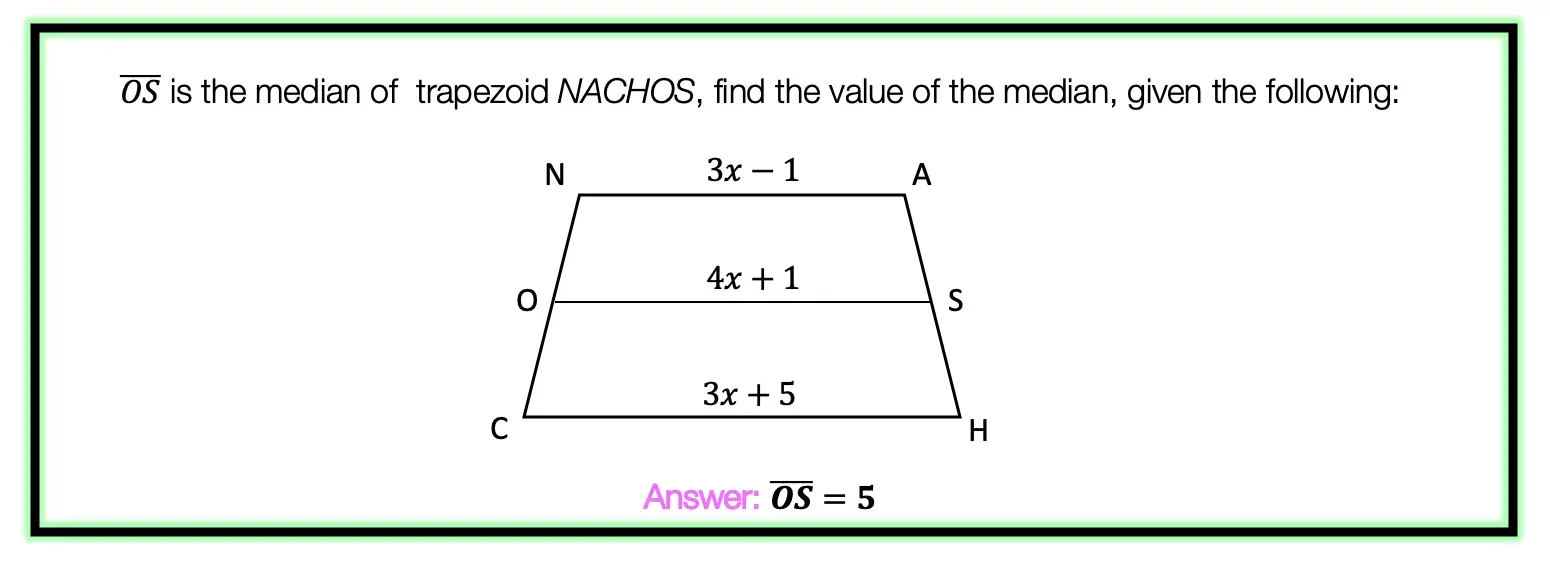
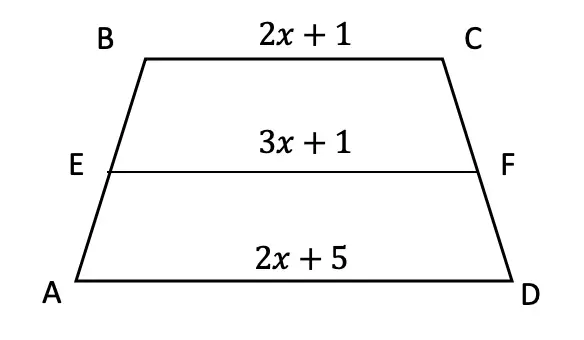
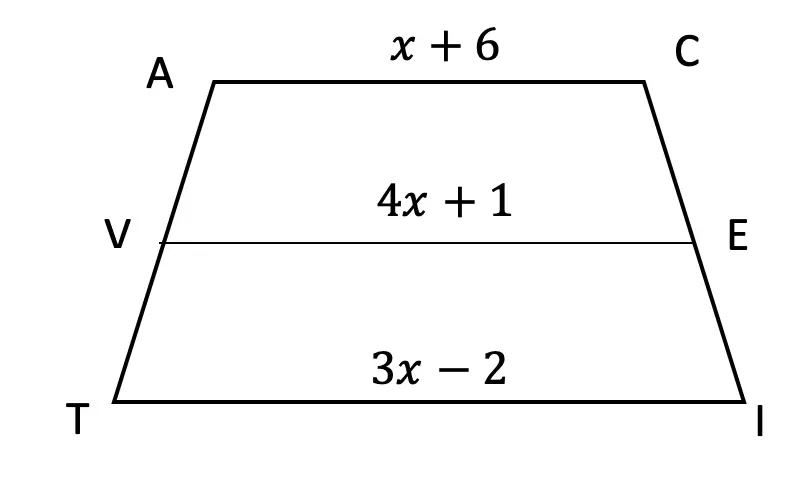
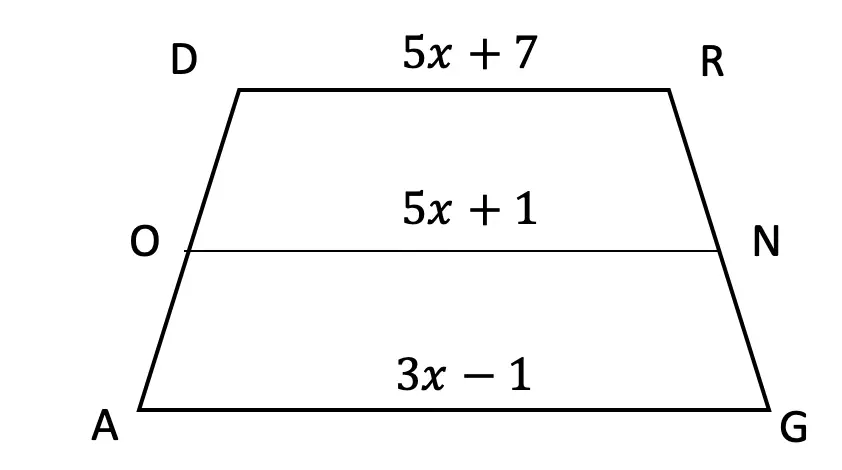
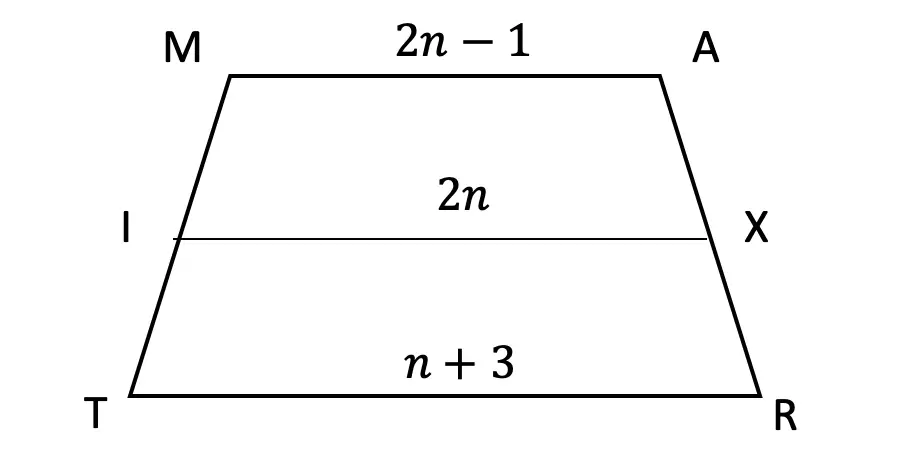
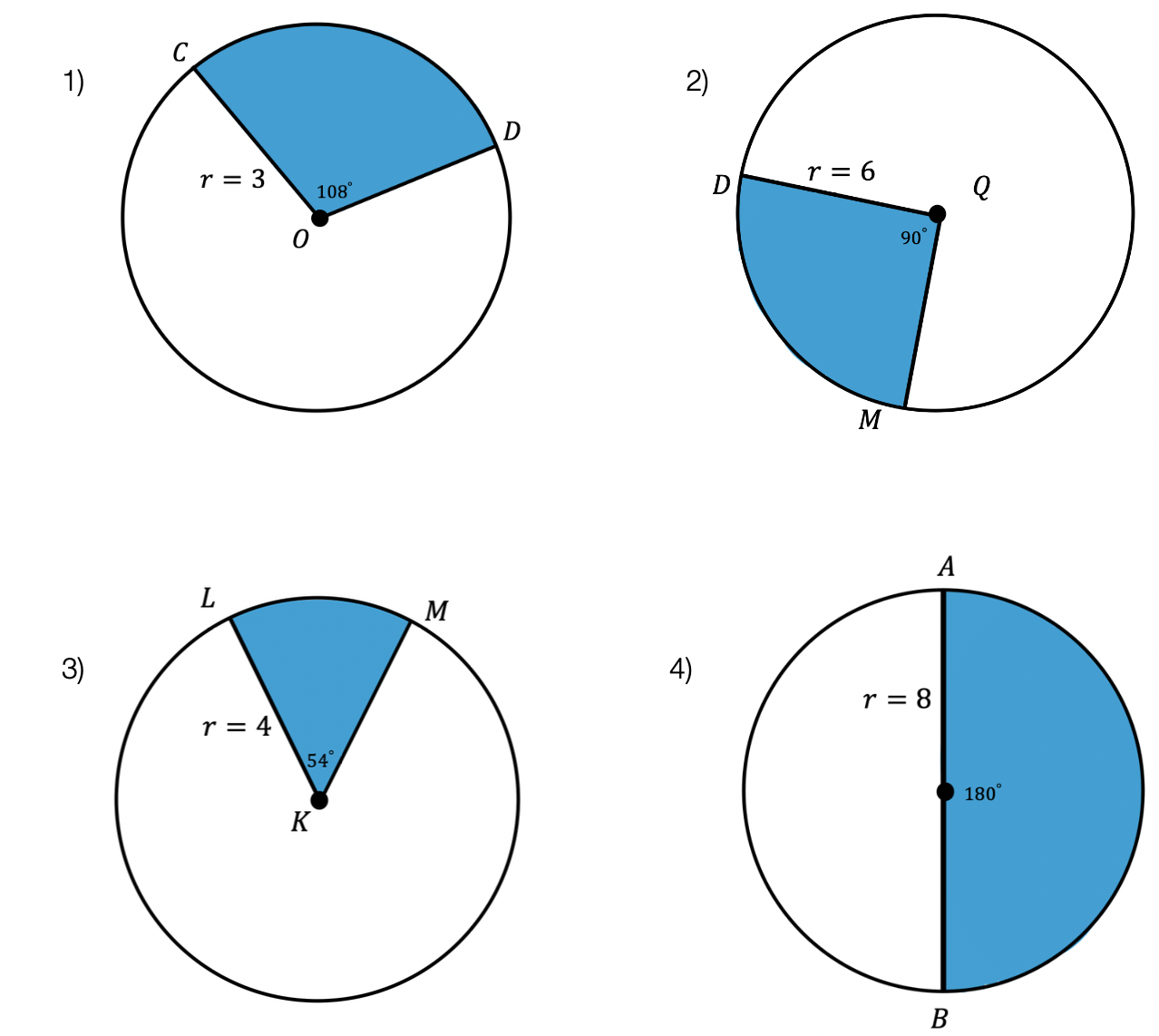
Try the following practice questions on your own!
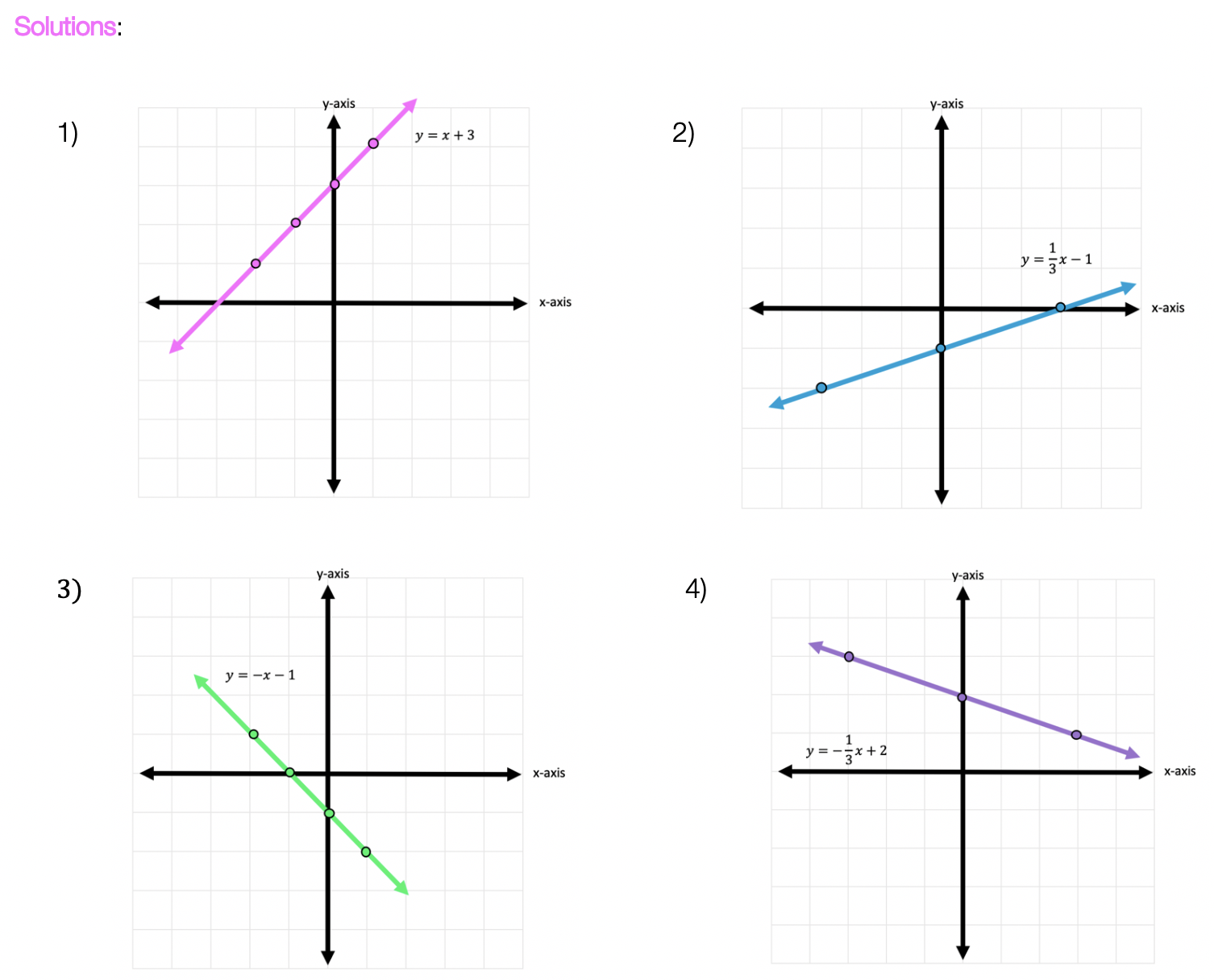
Practice Questions:
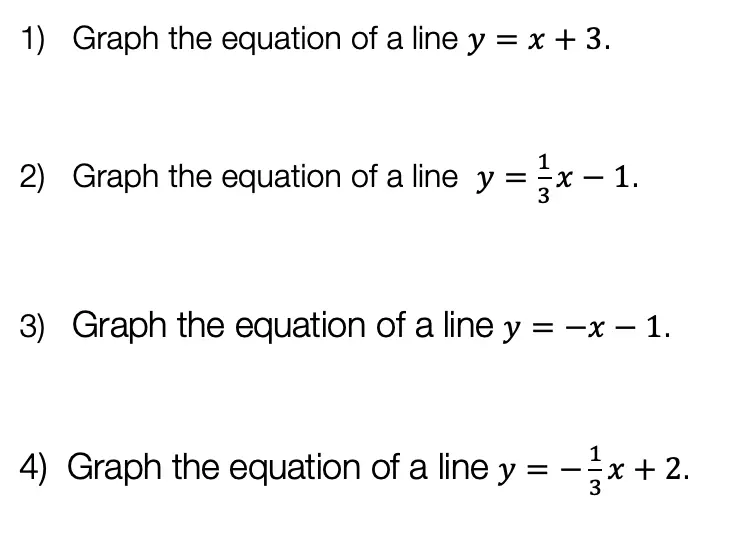
Want more Mathsux? Don’t forget to check out our Youtube channel and more below! And if you have any questions, please don’t hesitate to comment below. Happy Calculating! 🙂
Need to brush up on slope? Click here to see how to find the rate of change.